电化学阻抗谱是一种通用的实验技术,可提供有关电化学电池的各种物理和化学现象的信息。通过对相关物理过程进行建模,我们可以建设性地解释实验结果,并评估控制电池的物理量的大小。随后我们可以将模型转换成仿真 App,让更多的研究人员和工程技术人员可以进行电化学建模。本文中,我们将探讨三种不同的电化学阻抗谱分析方法:实验、模型和仿真 App。
电化学阻抗谱:实验
电化学阻抗谱(Electrochemical impedance spectroscopy,简称 EIS)是电化学领域广泛使用的实验方法,应用于电化学传感、电池和燃料电池的研究。这项技术的工作原理是,首先在固定电压下使电池极化,然后施加一个小的附加电压(偶尔施加电流)来干扰系统。扰动输入随时间作时谐振荡,产生交流电,如下图所示:
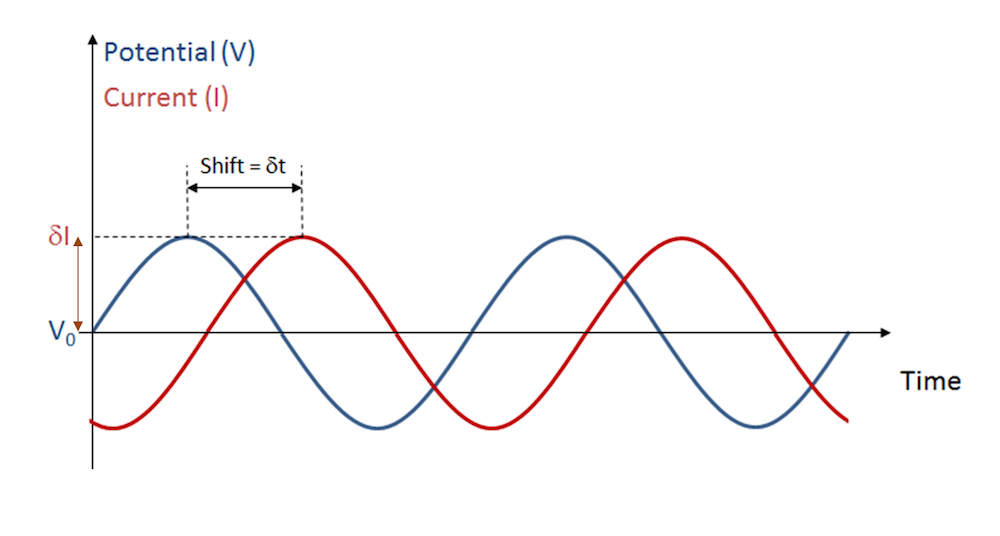
电池电压的振荡扰动产生振荡电流响应。
在特定幅度和频率的外加电压下,电化学电池产生频率相同的特定振幅的交流电。在实际系统中,对于其他频率的分量,响应也可能非常复杂,我们将在下文进行讨论。
在 EIS 实验中,我们通常在 mHz 到 kHz 范围内改变所施加的扰动的频率,响应的相对振幅以及输入信号与输出信号之间的时移(或相移)随施加的频率而变化。
这些因素取决于电化学电池中的物理过程对振荡激励的响应速度。不同的频率能够区分具有不同时间尺度的不同过程。在较低频率下,有时间进行的扩散或缓慢的电化学反应,以响应电池的交替极化;在较高频率下,外加激励比化学反应更快地改变方向,因此响应主要由双层充放电的电容决定。
时域响应不是解释这些频率相关振幅和相移的最简洁的方法。因此,我们定义了一个称为阻抗 的量。像静态系统中的电阻一样,阻抗是电压与电流的比值,但它使用复数的实部和虚部来表示振幅和相位与输入信号和输出响应的关系。将阻抗与时域响应联系起来的数学工具是傅立叶变换,它表示振荡信号的频率分量。
为了更全面地解释简单情况下的阻抗概念,我们将输入电压看作以角频率(ω)振荡的余弦波:
由此可见,响应也是余弦波,但具有相位偏移(φ)。与上图中的时移相比,相位偏移表示为 \phi = -\omega \,\delta t ,电流的大小及其相位偏移取决于电池的物理和化学性质。
现在,我们通过欧姆定律推导出电阻:
这个量随时间变化,其频率与扰动信号的频率相同。当分子等于零时,这个量值为零;当分母等于零时,值异常。因此,与直流系统中的电阻不同,它不是一个非常有用的量!
相反,根据欧拉定理,我们将时变量表示为复指数的实部,因此:
并且
我们将系数V_0和I_0\,\exp(i\phi) 分别表示为\bar{V} 和 \bar{I} 。
这些量是复振幅,可以根据原始时域正弦信号的傅立叶变换来理解,它们表示电压和电流的不同振幅和相位差。由于系统中的所有量都呈正弦振荡,因此我们通过比较这些复杂的量(而不是时域量)来理解物理效应。为了描述振荡问题(通常称为相量理论),我们将电阻的复数量模拟定义为:
这是系统的阻抗,顾名思义,是我们在电化学阻抗谱中测量的量,它是具有大小和相位的复数量,代表电阻和电容效应。电阻是复数阻抗的实部,与施加的电压同相,电容是复数阻抗的虚部,与施加的电压不同相。
EIS 专业人员以频谱的形式观察阻抗,通常使用奈奎斯特图,该图能够表现出阻抗虚部与实部的关系,在测量阻抗的每个频率下都有一个数据点。下图是一个仿真示例,我们将在下一节中讨论具体的建模过程。
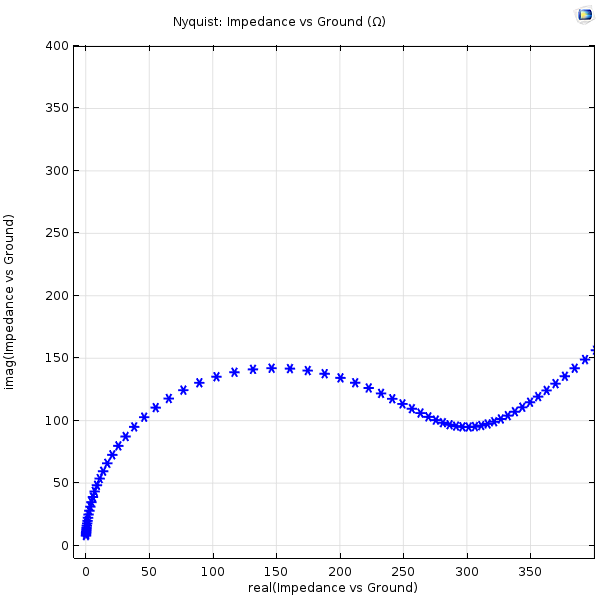
基于电化学阻抗谱实验的模拟奈奎斯特图。右上角的点处于低频率(mHz),左下角的点处于较高频率(>100 Hz)。
在上图中,左侧的半圆形区域显示了在快于物理扩散过程的频率下,双层电容与电极动力学效应之间的耦合,右侧的“扩散尾”对角线显示较低频率下的扩散效应。
由于 EIS 实验可以从一次分析中提取出许多不同物理效应的信息,因此这种实验非常有用。奈奎斯特图中的扩散系数、动力学速率常数和特征尺寸等属性之间存在定量关系。通常,EIS 实验是通过电阻和电容的“等效电路”来解释的,该电路产生的频率相关阻抗与上面奈奎斯特图中所示的阻抗相似。这个理念在我同事 Scott 编写的关于电化学阻抗和电容的博客文章中讨论过。
当电压与电流之间存在线性关系时,傅立叶变换中只会出现一个频率,从而可以大大简化分析过程。
为了解释阻抗方面的简谐波,我们需要电流响应以与输入电压相同的频率振荡,这意味着系统必须做出线性响应。对于电化学电池来说,我们通常可以通过确保外加电压比 RT/F 小来实现这一点,RT/F是气体常数和温度的乘积与法拉第常数的比值,这就是电化学中特有的“热电压”,在常温下约为 25 mV。较小的电压变化通常会引起线性响应,而较大的电压变化会引起明显的非线性响应。
当然,通过仿真来预测时域电流时,我们随时可以考虑非线性情况,并用数值方法进行傅立叶变换来研究其对阻抗的影响。实际上,上述阻抗解释最适合谐波假设。因此,阻抗测量通常以与瞬态技术互补的方式使用,如电流分析法或伏安法,这些技术更适合研究非线性效应或滞后效应。
我们来看一个支持这些理念的物理理论的简单示例,看看阻抗谱是如何与实际控制物理相联系的。
电化学阻抗谱:模型
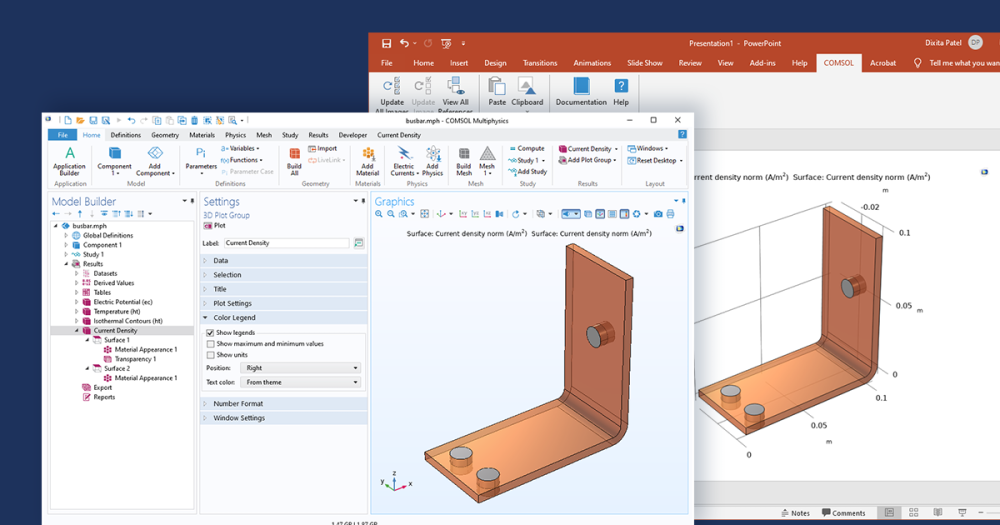
为了模拟 EIS 实验,我们必须描述关键的基础物理和化学效应,即电极动力学、双层电容和电化学反应物的扩散。在电分析系统中,大量人工添加的支持电解质使电场保持在较低水平,因此可以忽略溶液电阻。在这种情况下,我们可以使用扩散方程(菲克定律)描述系统中化学物质的质量传递,并利用合适的边界条件描述电极动力学和电容。在 COMSOL Multiphysics® 软件中,我们使用电分析 接口和“电极表面”边界特征来描述这些方程。
要了解有关如何建立此模型的更多详细信息,你可以在“案例库”中下载电化学阻抗谱教程示例。

EIS 模型中 “电分析”接口的模型树。
我们可以在传输属性 下指定所研究的氧化还原物质的扩散系数,至少需要一个氧化还原对的还原物质和氧化物质(例如常见的铁/铁氰化物氧化还原对)作为分析参考。“浓度”边界条件定义这些物质的固定本体浓度。“电极表面”边界特征的电极反应 和双层电容 子节点分别提供了法拉第电流和非法拉第电流。对于双层电容,我们通常使用经验测量的等效电容,并根据标准动力学方程(如 Butler-Volmer 方程)指定电极反应。
请注意,这里我们没有提到等效电路属性。在 COMSOL Multiphysics 中,电化学问题描述中的所有输入都是物理量或化学量,输出为奈奎斯特图。在反向分析问题时,我们可以通过实验中观察到的奈奎斯特图来推断这些物理和化学输入的实际值。
在“电极表面”特征的设置中,我们通过对电池电压施加谐波扰动 来表示阻抗实验。

EIS 模型中“电极表面”边界特征的设置。
其中,V_app 量表示外加电压。
谐波扰动是相对于电池上不变的稳定电压(或电流)施加的,在本例中,我们将稳定电压设置为零伏的参考值。对于较高级的模型,我们可以考虑使用另一个 COMSOL Multiphysics 模型(例如明显非线性模型)的结果来找到应用扰动的静止条件。如果你想更详细地了解谐波扰动的数学原理,请阅读我的同事 Walter 编写的这篇博客文章。
举个例子,在研究锂离子电池时,我们可以对电池的放电现象进行瞬态分析,研究电池的电荷传输、锂电解质的扩散和迁移,以及嵌入锂原子的电极动力学和扩散现象。我们可以在不同的时间暂停仿真,分析根据快速扰动测得的阻抗。要进一步了解其中的物理学原理,你可以阅读我的同事 Tommy 编写的关于锂离子电池电化学阻抗建模的博客文章。
电化学阻抗谱:仿真 App
电化学仿真的一个常见要求是仿真结果需“符合”实验数据,以便确定未知的物理量,或者更笼统地说,便于解释数据。即便是经验十足的电化学分析人员,也很难直观地“看到”像奈奎斯特图这样的基础图中的物理现象和化学反应。然而,通过在一系列条件下模拟这些绘图,我们可以揭示不同效应对整个图的影响。
仿真有助于分析 EIS,但对相关的专业人员来说也非常耗时。就像我以前的研究小组一样,专业人员可以花更多时间编写程序和运行模型,以便与实验研究人员一起整合数据,而不是将时间花在科学研究上。如果所有电化学研究人员都能将实验数据加载到一个简单的界面中,模拟给定物理模型和输入值的阻抗谱,甚至进行自动参数拟合,那该多好!好消息是,我们可以实现这一点!借助 COMSOL Multiphysics 中的“App 开发器”,我们可以基于基础模型创建一个易于使用的 EIS App。由于模型可以包含任意级别的物理细节,因此通过该 App 可以直接访问物理数据,而不仅仅局限于简单的等效电路。
为了重点阐述这一功能,我们基于“案例库”中的模型开发了一个 EIS 演示 App,该 App 的用户可以设置电活性物质的浓度,调节扩散系数以及电极动力学速率常数和双层电容。单击计算 按钮后,App 会生成可通过奈奎斯特图和波特图可视化的结果。
运行中的 EIS 仿真 App。
除了支持物理参数估计,该 App 对教学也很有帮助,我们可以快速改变其中的输入值,并将实验中可能出现的结果可视化。该 App 的一个自然扩展是将实验数据导入同一个奈奎斯特图中进行直接比较,我们也可以建立基础物理模型来分析竞争电化学反应的影响或电化学反应产物随后发生的均相化学反应。
结束语
本文中,我们介绍了电化学阻抗谱,讨论了一些建模方法,还探讨了如何通过一个基于简单理论模型构建的仿真 App 更深入地了解电化学系统理论与实验中观察到的现象之间的关系。
延伸阅读
- 探索 COMSOL 博客中与电化学仿真相关的其他主题




评论 (0)