
射线追踪是高频光学仿真的有效工具。COMSOL Multiphysics® 软件的射线光学模块使用了一种具有多物理场能力的波前方法进行射线追踪。在这篇博客中,我们将探讨 COMSOL Multiphysics 中的射线追踪算法与标准几何光学教科书中描述的传统射线追踪算法的不同之处,并提出一系列的实践建议,来帮助你获取最佳的仿真结果。
序列的、非序列的和精确的射线追踪算法
射线追踪算法可分为序列法 和非序列法。在射线光学模块中使用的射线追踪方法可以被归类为非序列波前法。
无论所使用的算法的细节如何,通过一个光学系统的射线追踪基本上是在两个交替的步骤中进行的。
- 给定一个初始位置和射线方向,无论是在物体上的某一点还是在光学系统中的某一表面,射线追踪算法确定射线将在哪里碰到下一个表面,并将射线追踪到该点。
- 接着,该算法继续通过在光线碰到表面的地方,施加边界条件(如反射或折射)来调整光线方向。这样就能改变反射或折射光线的方向,为其在后续介质中的追踪做准备。
即使在有大量表面的复杂系统中,整个射线追踪过程通常也可以分解为这两个步骤的连续迭代,如下图所示。
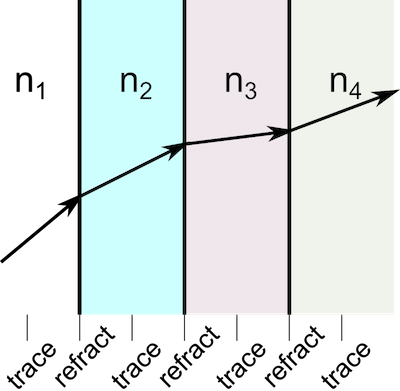
在一些关于几何光学的标准文献中描述了几种序列射线追踪算法(例如,见参考文献1、2 和 3)。所谓序列射线追踪,是指光线遇到的光线或镜子的序列被指定为射线追踪算法的输入;换句话说,你知道光线将首先通过透镜 1,然后是透镜 2,以此类推,但你不知道光线将在哪里通过每个透镜表面,或反射和折射光线的角度是什么。
在非序列的射线追踪方法中,光线遇到透镜和镜子的序列并没有事先指定。相反,如果指定了光源,该方法将自动确定光线和系统中的光学元件之间的相互作用。
一些重要的序列射线追踪算法利用了旁轴近似法,并假定光线与光轴之间的角度很小。相比之下,某些序列和非序列射线追踪方法可以归类为精确方法(1,2,3),因为在预测光线与透镜表面的交点时,会考虑到透镜的形状,而不使用旁轴近似。因此,光线与弧形透镜的实际表面相交,而不是顶点平面。
在精确的分析性射线追踪方法中,光线与透镜或镜子表面的交点是通过求解一个代数方程来计算的。例如,如果透镜的表面是球形的,那么给定光线的初始位置和方向,它与透镜表面的交点可以通过求解一个二次方程精确计算出来。对于更复杂的非球形表面,光线与表面的交点的方程可能没有一个封闭的分析解,可能需要一个数值方法。
在下面的讨论中,我们将把 COMSOL® 软件中使用的方法与上面描述的精确射线追踪方法进行比较。我们将忽略较简单的旁轴光学方法,因为 COMSOL Multiphysics 中的射线追踪总是使用斯奈尔定律(Snell’s law)的完整实现,而从不使用小角度近似。
均质材料与渐变折射率材料的比较
许多传统的射线追踪方法要求每种材料都是均匀的;也就是说,折射率在每种介质中的梯度为零,只在边界处不连续地变化。如上所述,基于代数求解与下一个透镜的交点的方法,只适用于非梯度介质。这是因为渐变折射率介质中的光线可能是弯曲的,所以光线的初始位置和方向不足以确定它将在哪里与表面相交。
真实世界中的光学系统可能会因为设计或多物理效应而拥有具有渐变折射率或不均匀的元件。设计中的渐变折射率分布的例子包括 Luneburg 透镜、麦克斯韦的鱼眼透镜和通过电泳制造的 GRIN 透镜。在非均匀温度分布的环境下的透镜,由于材料特性取决于温度和应变,会不经意间出现渐变的折射率。这些是波前法擅长的一些最重要的情况。
下图显示了异质介质中射线路径的一个例子。在图片中,热学色表显示了建模域的温度,浅色对应于较高的温度。折射率的变化与温度的变化成正比,因此在温度梯度最大的地方,射线路径变得更加明显弯曲。沿着射线路径的颜色显示了射线的瞬时群速度幅度,最大的幅度显示为红色,最低的幅度为蓝色和紫色。出于演示的目的,这个模拟被夸大了,从概念上描述了激光系统中泵浦激光晶体的情况。
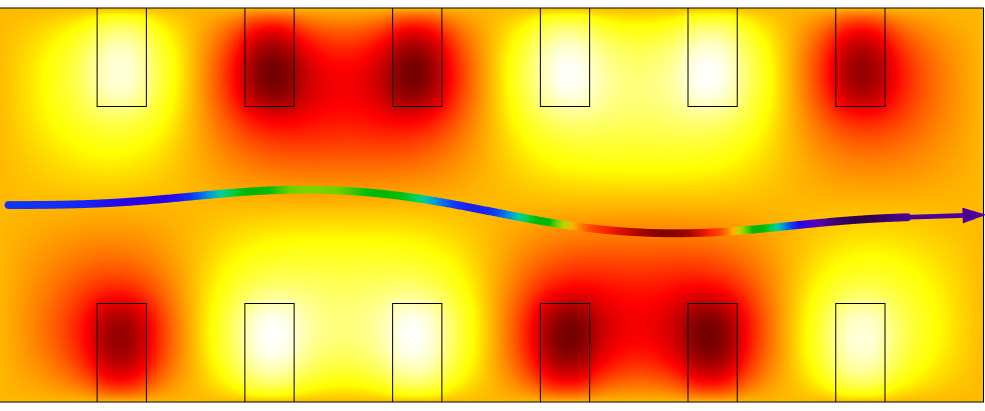
一条射线沿着弯曲的路径(夸张的)穿过加热的材料。
波前射线追踪法
COMSOL Multiphysics 中的射线追踪方法对瞬间射线位置 q 和波矢量 k 分量的一组耦合一阶常微分方程(ODE)进行数值求解。
{\mathbf q} }{ \partial t} = \frac{ \partial \omega( {\mathbf k} )}{\partial {\mathbf k} }
}
其中,角频率 ω 取代了通常由哈密顿算符 H 占据的位置(参考文献4)。
当折射率是均匀的,上面的哈密顿公式被简化为说明光的恒定速度和射线方向的表达式,如下所示:
当界面上的折射率不连续时,COMSOL Multiphysics 利用斯涅尔定律(Snell’s law)数值计算折射光线的方向。这个公式使 COMSOL® 软件不仅可以计算同质折射率的特殊情况,而且可以计算更多的一般情况,如激光工程中的热透镜(包括直线和弯曲的光线)。请注意,这是一种时间步法,结果显示了传播过程中不同时间段的射线。
表面的离散化和几何形函数的阶次
举一个几何形状的例子,考虑一个旋转对称的非球面透镜表面凹陷,由以下分析表达式描述:
(1)
这里,z, \ c,\ k, \ A_i \ (i=1,2,\cdots) 分别是透镜表面凹陷、曲率、圆锥常数和偶次多项式的系数;r^2=x^2+y^2,其中 x 和 y 是横跨光轴的两个方向。
在 COMSOL Multiphysics 中,透镜和镜子的形状可以作为解析函数或完整的三维 CAD 模型输入。分析给定的形状被输入为参数曲线或曲面,并由高阶非均匀有理样条(NURBS)近似。在下一步骤中,曲面(或曲线)用有限元网格进行近似,用多项式进一步近似形状。
在用户界面上,这些多项式的最大阶数由模型组件的设置窗口中的几何形函数阶次 决定。这些近似的精度可以通过细化网格和/或增加几何形函数阶次来提高。然后,射线与各个网格单元相互作用,用于预测交汇点和应用斯涅尔定律。
在大多数情况下,几何形函数阶次的默认选项 Automatic 是使用二次多项式来近似曲面,但有时也会使用线性形函数阶次来避免创建倒置的网格单元。对于大多数应用来说,用户可以将阶数提高到七阶(Septic)多项式。
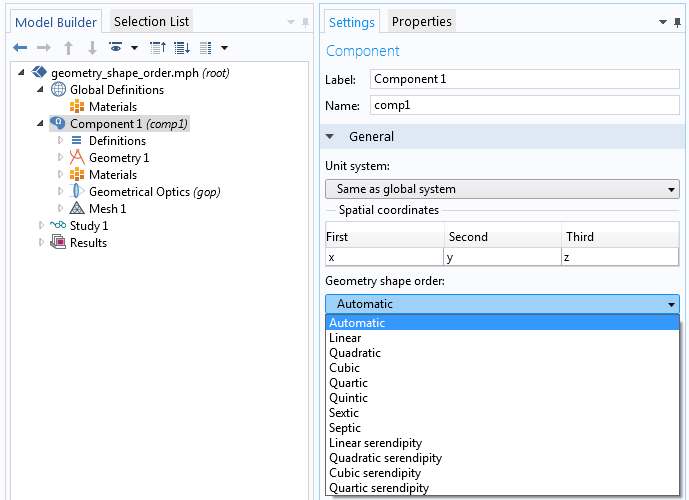
几何形函数阶次的设置窗口
现在我们来考虑一个非球面透镜,它的形状在前面已经描述过了。为了更容易看到离散化,这里的透镜使用了非常粗的网格。在下面的图中,线性化的网格单元用灰线表示,而曲面的数值表示则用黑色的轮廓表示。
左图是默认(自动,即大部分为二次元)设置下的射线追踪结果,右图是使用线性几何形函数阶次的情况。射线的颜色代表波矢量的 Y 分量(垂直轴)。可以通过寻找颜色变化的位置来了解射线被折射的位置。在任何几何形函数阶次的选择中,表面形状不能再由上述非球面公式来写;也就是说,它是一个片状连续多项式的集合,其阶次由几何形函数阶次 的设置来决定。
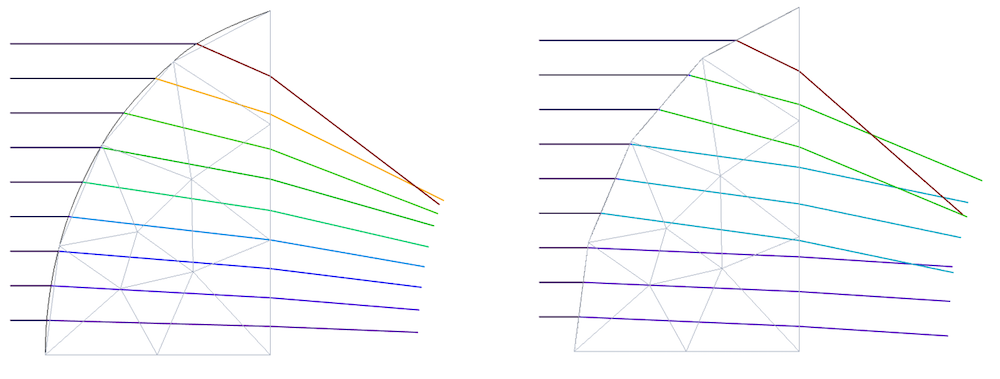
一个非球面透镜表面和它的近似表面形状使用二次(左)和线性(右)几何形函数阶次。
射线和有限元网格
COMSOL Multiphysics 中的射线追踪算法使用有限元网格在表面反射和折射射线的原因有几个。如前所述,强调了 COMSOL® 软件作为多物理场仿真工具的优势,因为它使追踪射线通过渐变折射率介质成为可能,在这种介质中,折射率分布是由另一个物理界面计算的场的函数。另一种情况是,当透镜表面由于热膨胀或由于透镜上的其他外力而变形时,可能无法得到透镜表面的解析表达。总之,几乎所有与光学系统耦合的物理学都是用有限元方法建模的,所以耦合是通过有限元网格进行的。
由于射线追踪算法使用有限元网格,在 COMSOL Multiphysics 中进行射线追踪的最低要求是所有反射或折射射线的边界必须有一个边界网格。边界网格单元用于计算表面属性,如法线方向和主曲率半径,这在射线反射或折射时是需要的。边界网格还为网格搜索算法提供信息,预测射线到达边界的瞬间,使沿射线路径计算的数量,如强度和相位,得到更准确的计算。
在某些情况下,射线传播的域也应该有一个域级的有限元网格。例如,包含渐变折射率介质的域必须始终被网格化。如果折射率与温度有关,那么为了计算射线在介质中的瞬时位置的折射率,有必要从温度场查询一个值。温度可以使用网格单元中定义的有限元基函数在射线的准确位置上进行插值。然后,这个温度值可以被替换成与温度有关的折射率表达式。
当射线在吸收性介质中传播时,也需要一个域级网格。介质中的沉积射线功率是用定义在网格单元上的分片不连续函数来离散的,所以网格是必要的,以便将每条射线对总热源的贡献限制在一个有限的范围。
网格分辨率如何影响解
到目前为止,我们已经了解到,COMSOL® 软件中的射线追踪是一种近似的解,它将每个表面视为基于有限元网格的分片连续多项式。因此,解的精度取决于网格的分辨率。更高的几何形函数阶次和更细的网格可以减少离散误差。在上图的右图中,一些射线通过了相同的边界单元,这就虚假地导致了相同的波矢量(颜色相同的线)。这是一种近似误差,当几何形函数阶次较低且网格非常粗时,我们可以明显看到这种误差。
下面的图显示了在前面的例子中,被同一个透镜第一次折射后的折射光线的单位波矢量的Y分量。横轴代表Y轴上的初始射线位置。当几何形函数阶次为线性时,由未充分解析的网格引入的误差是最显著的。
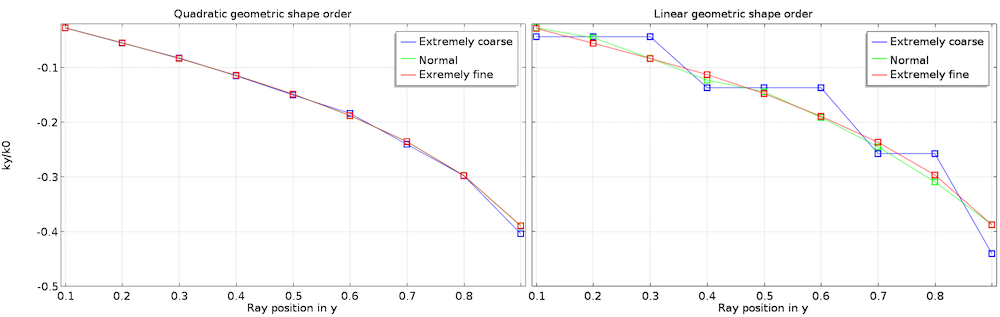
用不同的网格单元大小(用不同颜色表示)绘制的二次几何形函数阶次(左)和线性形函数阶次(右)的单位波矢量的Y分量图。
网格细化对点状图的影响
我们已经看到,网格细化程度会影响到射线轨迹的精度,所以它也会影响到点阵图的精度,这一点应该不奇怪。如果初始射线位置和方向的分布是对称和有规律的,那么精确的射线追踪方法的结果通常显示出近乎完美的对称性和连续性。非球面透镜的光斑图总是围绕着光轴对称的,而且射线畸变总是平滑和连续的。对于基于有限元的波前方法,只有当网格继承了原始透镜几何的对称性时,其结果才是对称的。
即使对于具有对称的射线位置和方向初始分布的对称光学系统,如果网格不对称,COMSOL Multiphysics 中的射线追踪结果也会给你带来轻微的不对称结果。但随着网格的细化,这些偏离对称性的情况会逐渐减少,因为对称面两侧较小的网格单元会向相同的表面表示法靠拢。这只是网格离散性误差的另一种表现形式。通过使用结构化的网格可以提高解的对称性。然而,需要注意的是,对称的解并不一定意味着解更准确。
下图显示了最大网格元大小对光斑图的影响,以及一个平凸透镜的RMS光斑半径图。这个聚焦透镜被设计为有一个衍射限制的光斑。可以看到,随着网格尺寸的下降,RMS 光斑半径是如何收敛到某一数值的,和预期的那样。让我们再仔细看看。最粗的网格的光斑比衍射极限大。它也是非常不对称的,交点分布在一个非常大的区域。这种网格大小对于其他物理学问题,如热和力学问题,看起来并不是特别糟糕。然而,对于使用默认的自动几何形函数阶次的射线追踪,这个网格太粗了,无法产生准确的点阵图。只有最后两种尺寸的网格可以产生一个集中的、对称的光斑。
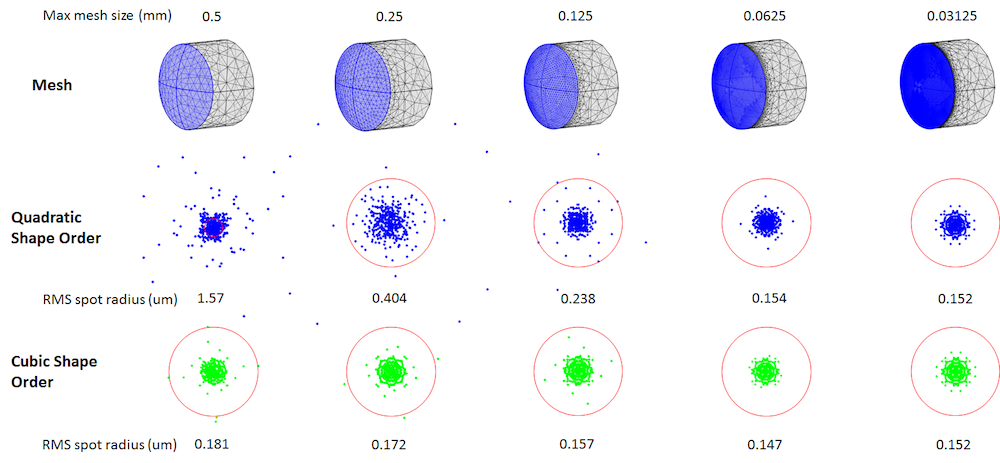
取决于最大的网格大小的二次和三次几何形函数阶次在焦点处的光斑图的比较。红色圆圈显示了波长为0.66um 的透镜的衍射极限尺寸。
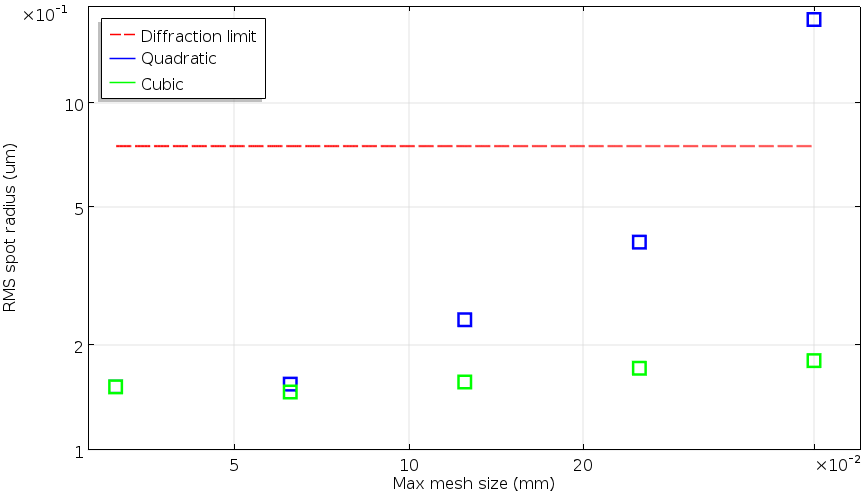
与衍射极限尺寸相比,二次和三次几何形函数阶次的 RMS 光斑半径作为最大网格大小的函数的双对数图。
解释 COMSOL Multiphysics®中射线追踪法产生的解数据
现在让我们来看看解数据的格式与上述传统(稳态)分析射线追踪算法的格式有什么不同。
下面是一个例子,它比较了 COMSOL Multiphysics 中得到的随时间变化的解和前面例子中同一聚焦透镜的标准序列光线追踪平面到平面方法的典型输出。一个平凸透镜将光线聚焦到一个光点。在我们熟悉的传统平面对平面方法的结果中,所有的光线都被引向端面。另一方面,在 COMSOL Multiphysics 中,每条射线都被绘制到了指定时间步长的射线所处的位置。所以,一般来说,射线不会铺设在同一平面上。
这就是为什么 COMSOL Multiphysics 中的射线轨迹结果几乎总是显示一些曲率。这个曲率不过是几何光学体系中的波前。在这个例子中,波前是由透镜引入到射线的二次相位函数所弯曲的。为了将所有的射线引向端面,要使用较久的求解时间,以便所有的射线都有足够的时间到达端面并停止传播。

COMSOL Multiphysics® 中随时间变化的射线追踪的仿真结果(左)和标准序列的平面到平面的射线追踪(右)。
虽然看到原始波面很方便,但我们需要确保我们模拟的所有射线都已经通过了我们想要计算数量的平面。下面的连续点阵图说明了上述例子在不同求解时间的点阵图。在 COMSOL Multiphysics 中,点图是用 Poincaré Map 绘图类型生成的。由于波前是收敛的,外侧射线先到达平面,内侧射线后到达。因此,平面内的计算可能因我们选择的时间不同而不同。
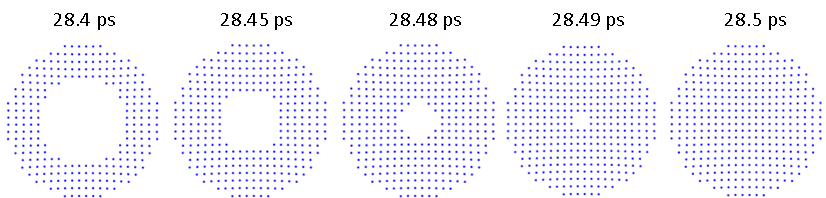
在不同的求解时间产生的点状图。
为了确保我们计算我们感兴趣的平面内的所有射线,COMSOL Multiphysics 配备了称为 attimemin 和 attimemax 的算子。例如,下面的表达式给出了 x = 0.1 m 的 yz 平面内的 RMS 光斑半径。
sqrt( gop.gopaveop1( attimemin(0,0.4[ns],(qx-0.1[m])^2, qy^2+qz^2) ) )
gop.gopaveop1() 算子取括号中的表达式在所有射线上的平均值。这个算子的参数为
attimemin(0,0.4[ns],(qx-0.1[m])^2, qy^2+qz^2)
调用 attimemin 算子,它需要四个参数。
attimemin 的前两个参数定义了我们要计算表达式的最小值的时间段的开始和结束。我们必须确保射线穿过平面的时间是在这个范围内。第三个参数是要最小化的表达式。在检测到射线的这个第三个参数的最小值时,将返回第四个参数的值。 attimemin 算子使用了存储的求解时间之间的插值,所以有可能准确地得到每条射线与平面的交点,即使这个交点与存储在求解中的时间步长不一致。
换句话说,前面的表达式可能是这样的。
“计算所有射线在 0 到 0.4ns 之间的径向坐标值的平均值的平方根,对于这个时间,射线与平面 x = 0.1 的距离达到最小。”
下一个例子显示了当射线在边界处发生反射或折射时,以离散的时间步长存储的解是如何影响轨迹图的。我们通常不会事先知道每条射线与每个表面相互作用的确切时间或光路长度,所以这些相交时间通常不会与存储的解的时间完全吻合。因此, COMSOL Multiphysics 射线追踪结果显示,在界面或反射壁附近的轨迹有一些小的不完整,如下图所示,射线似乎在离边界不远的地方改变了方向,而不是正好在边界上。然而,对于这种随时间变化的射线追踪方法来说,这是预料之中的事情,并不影响其准确性。即使射线在结果中看起来没有撞到界面或壁,COMSOL® 软件也会为每条射线计算出准确的交互时间,通常使用二阶泰勒法从先前存储的求解算=时间推算出射线位置。

射线在反射壁处的反射。在图中,并非所有的射线都被定格在壁上,但所有的射线轨迹都被准确计算出来。
结语
在这篇博客中,我们讨论了 COMSOL Multiphysics 中用于射线光学模拟的独特的随时间变化和基于网格的方法。还介绍了在射线追踪结果中可能会遇到哪些类型的异常,特别是当时间步较大、网格较粗的时候。与其他物理界面一样,细化网格或提高时间分辨率可以清除这些看起来不正常的行为,并产生精确、收敛的解。
更多资源
在 COMSOL 博客上了解更多关于 COMSOL Multiphysics 的射线光学和射线追踪功能。
参考文献
- R.R. Shannon, The Art and Science of Optical Design, Cambridge, 1997.
- D.C. O’Shea, Elements of Modern Optical Design, Wiley, 1985.
- R. Ditteon, Modern Geometrical Optics, Wiley, 1998.
- L.D. Landau and E.M. Lifshitz, The Classical Theory of Fields, 4th ed., Butterworth-Heinemann, Oxford, 1975.






评论 (0)