我们经常遇到这样一个问题:当存在奇点时,评估应力的最佳方法是什么?最准确的回答是:尽量避免评估应力。但是,这对实际工程帮助不大。这篇博客,我们将深入探讨奇异应力场的特性,并讨论一些可行的评估方法。
本文是博客:“有限元模型中的奇异现象:如何处理模型中的红点”的后续内容,介绍了结构力学模型中出现奇异应力的时间和原因,并对奇异现象进行了一般性介绍。如果您是第一次了解该主题,建议先阅读这篇博客。有关如何处理奇异应力场的详细信息,请阅读本文。
进一步了解奇异应力场
首先,我们来详细分析一下奇异应力场及其与应力集中的关系。应力集中也出现在几何不连续处,二者有相似之处。应力集中与奇点的区别在于,前者的最大应力是有边界的。例如,您可以通过在有限元模型中使用足够精细的网格获得精确解。
通常,机械设计人员会通过引入一个半径尽可能大的圆角来减少应力集中。应力集中处的峰值应力通常用应力集中系数 K_{\mathrm t} 与适当选定的名义应力的乘积描述。对于圆角,有时可以通过下列表达式获得 K_{\mathrm t}:
式中, \rho 是圆角半径,L_\mathrm{char} 是以圆角结束处缺口的特征长度。
该方程的背景是求解一个大平板中的椭圆孔处应力集中的解析解,其中 L_\mathrm{char} 是椭圆较大的半轴的长度。
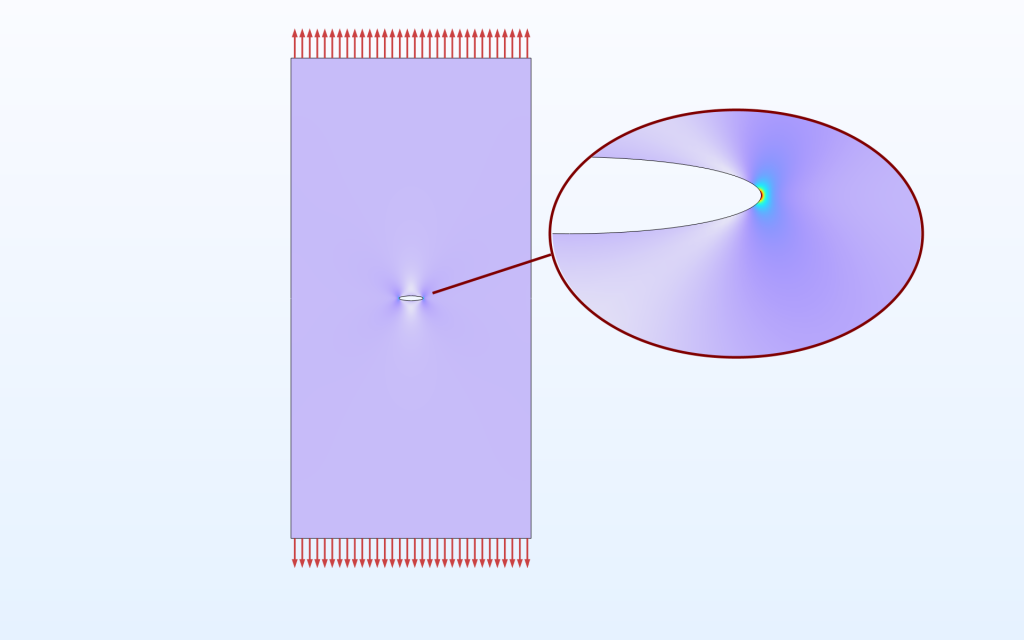
含一个椭圆孔的大平板。
对于大多数缺口,该表达式只能用于粗略计算 K_{\mathrm t},因为很难推导出特征长度。一个重要的事实是:小缺口处的峰值应力基本上是圆角半径平方根的倒数。相信任何尝试过减小局部应力集中的工程师都可能为这一事实而苦恼过,因为适度地增大圆角半径会使峰值应力更适度地减小。
极限应力集中发生在裂纹尖端,此处缺口半径无限小。在弹性固体中,裂纹尖端附近的应力场和应变场的解是众所周知的。它们与裂纹尖端距离的平方根(r)成反比。应力场通常写成
式中,K_I, K_{II}, 和 K_{III} 分别是模式 I(开口)、模式 II(剪切)和模式 III(撕裂)的应力强度因子。函数 f, g, 和 h 由裂纹尖端周围极角 \theta 的三角函数组成。(更详细的定义请参见此处)。
一个令人惊讶的结论是,只要 离裂纹尖端足够近 ,裂纹尖端周围的应力场看起来是一样的,与裂纹的实际形状以及裂纹所在的成分无关。
在线性弹性断裂力学的假设条件下,模式 I 的断裂准则为 K_I = K_{Ic},其中 K_{Ic} 是材料参数(称为 断裂韧性)。这样,就可以在不明确使用无限应力的情况下研究这种具有特殊奇异性的几何形状。这个思路将在下文中得到推广应用。
现在,考虑一种几何形状几乎是奇点的情况。也就是说,一个圆角或一个圆角半径很小的裂纹。本文将重点讨论这种情况。在距离较远处,我们无法真正区分缺口和奇点。接下来,我们将使用一个例子来解释这句话。
以一个处于拉伸状态的含缺口的长条几何的二维模型为例。通过在这个模型中沿左侧垂直边添加对称条件,也可以研究内部缝隙。
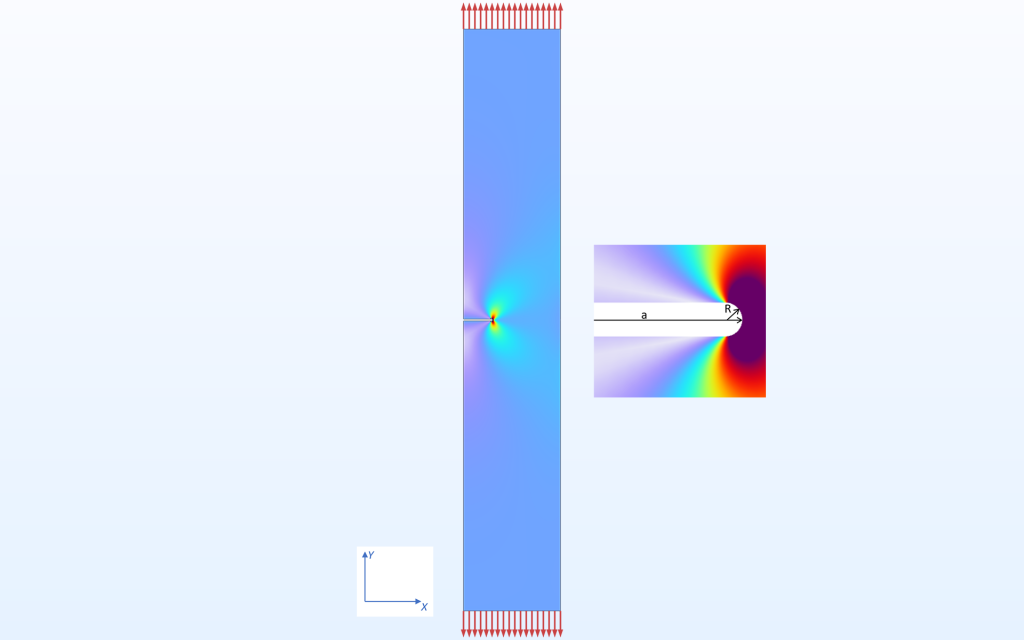
含缺口的长条几何结构的应力分布。该模型的参数与缺口深度 (a) 和缺口半径 (R) 有关。
首先,可以注意到,对于尖锐的裂纹,这种几何形状的应力强度因子可写成
a 是裂纹长度; \sigma 是外加应力(此处为 1 Pa); W 是长条宽度。函数 f 有多种表示方法。在此,我们使用以下表达式
这个表达式在本文被称作 裂纹解。
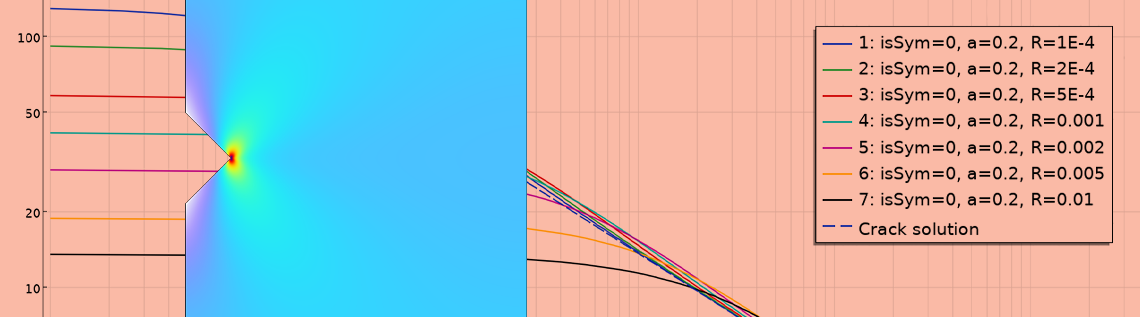
沿韧带(从切口尖端向 x 方向延伸)的应力分布图,适用于短切口和几种不同的切口半径。由于对称性,只有一个应力分量 c 不为零。

不同缺口半径下沿韧带的垂直应力与缺口尖端距离的函数关系。虚线表示相同深度的裂纹的理论值。
一个有趣的现象是,在特定情况下,应力场与裂纹解析解的应力场非常相似,即应力-距离对数图中的直线。在靠近缺口的地方,应力是有边界的,因为它是一个缺口,而不是裂纹。不出所料,峰值应力与 1/\sqrt{R} 成正比。
在远离尖端的地方,裂纹的局部应力场解在任何情况下都是无效的,不管它是裂纹还是缺口。但在非常近和非常远之间的区域,无论是从观察的角度,还是从物理学和数学的角度来看,都无法真正推断出缺口尖端的真实形状。
为什么这一点很重要?如果知道缺口的形状,那么只要观察一定距离外的应力,就可以确定那里的应力。稍后将详细探讨这一想法。
下一步,我们将在同一图表中绘制大量具有不同缺口半径和切口长度的应力图。不过,现在的横轴通过缺口半径 R 进行了归一化处理。

不同缺口深度和半径下,沿韧带的垂直应力与缺口尖端距离的函数关系。
从图中可以看出,在距缺口尖端的距离小于尖端半径 0.7R 时,进入恒定斜率区域。从我们的角度来看,这已经相当接近要求解的问题了。那么这个区域会延伸多长呢?这不是由缺口细节控制的,而是由几何尺寸控制的。通过另一个归一化曲线图,韧带长度 (W-a),可以得知这一信息。
因此得出以下结论,这种情况下的恒定斜率区域延伸到韧带的 10% 左右。再远一些,应力场就不再受裂纹解的控制,而是受更多全局属性控制。对于特定几何来说,这一区域的大小取决于该几何特有的长度尺度。
接下来,我们来研究是否可以用裂纹解中的应力场预测缺口尖端的峰值应力。先回到大平板上的椭圆孔。椭圆孔(宽度为a,缺口半径为R )的峰值应力与裂纹(长度为 a)的应力强度因子之比为
假定 R << a,则峰值应力可用应力强度系数表示为
这样,当计算出应力强度因子时,就可以用以下表达式确定圆形裂纹尖端的应力了。
其中,系数 \beta 是一个与配置相关的数量级为1的数字。我们可以在上面的例子中尝试这一假设。
下面绘图显示的表达式
为缺口半径与缺口深度的函数关系。使用了两种不同的几何形状:边缘缺口和中央狭缝。后一种情况是通过在模型中添加对称条件获得的。
使用有边缘缺口的几何得到的系数 \beta。
使用中心狭缝的几何得到的系数 \beta。
可以看出,只要缺口半径较小,两种情况下假定的乘数 \beta 的实际值都接近 1.2。缺口半径大、长度小的情况下,与裂纹的相似度就会降低。使用 R<< a 进行简化是无效的。
为了绘制这些图,我们使用了 K_I 的解析值。在实际情况中,如果不知道这个值,则可以使用距缺口一定距离的解,通过数值计算确定 K_I 。
事实上,任何尖角都有一个应力场衰减为 r^{-p} 的区域,其中 r 是与尖角的距离。到目前为止,我们已经看到理想的裂纹 p = 0.5 。不同开口角度下的 p 值如下图所示。
不同开口角度下应力奇点衰减的幂次。突出显示了 45°、90°和 135° 的值。
这条曲线是通过求解超越方程
\sin \left ((1-p)(2\pi-\alpha) \right) +(1-p) \sin(2\pi-\alpha) = 0, \alpha 为开口角度。
为了完整起见,我们可以在含内角的长条拉伸有限元模型中检验超越方程的解。该模型使用拐角的开口角度作为参数。

开口角度为 90°时,含内角的模型中的 von Mises 应力 。

沿韧带的垂直应力。离尖角的距离通过韧带长度进行了归一化处理。虚线表示根据上述 p 值得出的理论解。
可以看出,应力-距离图中有一些几乎是直线的区域,在拐角附近与理论斜率非常接近。
另一种奇点是由材料不连续性引起的。在实践中,这通常与几何奇点同时出现。在此,我们仅研究长条在拉力作用下的纯材料不连续性。
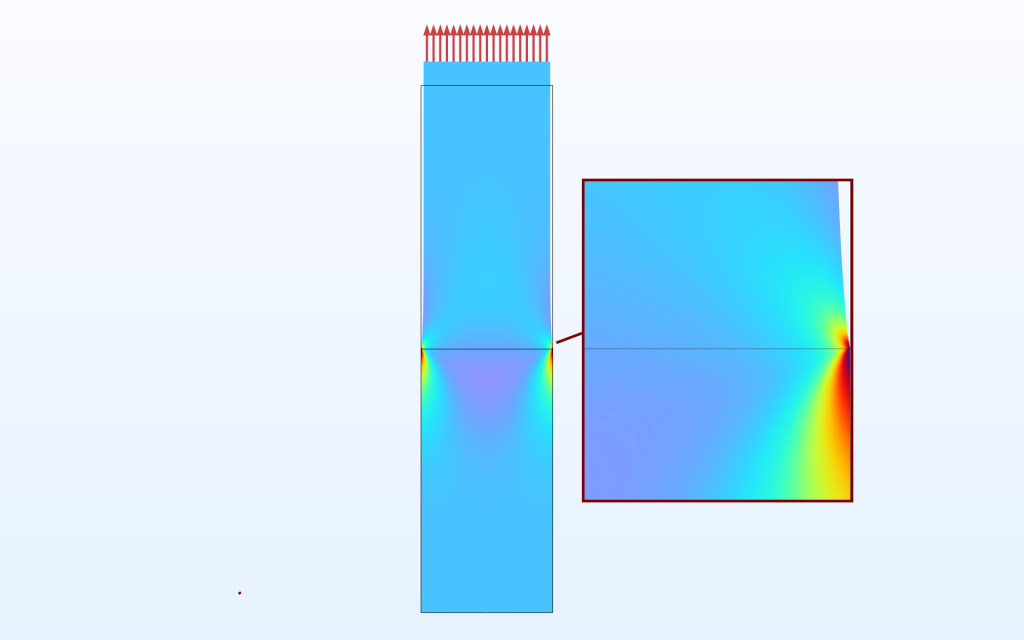
一根下部比上部硬的长条杆的模型几何,绘制了载荷方向的应力。
从这第一幅图中就已经可以看出一些通用特性:
- 自由表面出现奇点。
- 硬质材料的应力高于相应位置的软质材料应力。
为了更深入地研究这个问题,我们可以绘制显示应力衰减与材料界面距离的函数关系的图。

沿自由边界加载方向上的应力与界面距离的函数关系图。实线表示软质材料的应力结果,虚线表示硬质材料的应力结果。参数 r 是软质材料与硬质材料的杨氏模量比值。
同样,可以在应力-距离对数图中发现一些直线,这表明应力随距离的变化而变化,如 r^{-p} 。在两种材料中,幂 ‘p’是相同的(用相同颜色表示的实线和虚线是平行)。奇点的强度受两种弹性模量的比值和泊松比值的控制。
观察上述(放大的)表面图中的变形形状,我们可以从物理角度对此进行解释:在相同载荷下,较软的材料比较硬的材料延伸得更多。也就是说,在软质材料中,载荷方向上的应变变大。这也意味着,在两种材料具有相同泊松比的情况下,横向收缩也会相应增大。不过,这种收缩会在两种材料的界面处受到抑制,从而产生局部应力奇点。
如果选择
这个奇点就会完全消失。
得出的结论是,在大多数情况下,材料变化会产生奇点。此外,在这种情况下,不连续性附近会有一个区域,应力会根据幂律衰减。
现在,我们已经研究了有限元仿真中最常见的奇点类型,并发现它们有一个共同的特性:奇点附近的应力与距离呈幂律关系。
焊缝评估
对焊缝进行设计以使其能够安全地应对失效是工程领域的一项重要功课。尽管在一般情况下不可能精确地进行应力评估,但已有大量研究致力于提供预测失效的系统方法。对于这种情况,造成问题的主要原因是焊缝的实际几何形状未知。根据确切的局部几何形状,焊缝可能会也可能不会引入应力奇点。更为复杂的是,焊缝中往往存在隐性缺陷。除了需要高质量焊缝的情况,在这种情况下可以对焊缝进行打磨,并采用某种无损检测方法进行检查。但大多数情况下,对焊缝进行详细的局部应力分析意义不大。

有三种不同局部几何形状的圆角焊缝。
COMSOL博客:“如何预测焊缝的疲劳寿命”介绍了焊缝的应力评估。
与其深入探讨焊缝分析的细节,不如探讨更有意思的焊缝设计理念:
- 计算指定位置的应力,而不是焊趾本身的应力。
- 确定该应力的允许值,这通常必须通过实验来完成。
- 允许的应力值取决于您同意评估应力的方式和位置,因此它不是真正的材料属性。
在使用纸和笔计算的年代,所有局部效应都被忽略了。允许的应力值必须考虑到这一点,因此往往偏低。现代基于有限元的方法考虑了部分应力集中(由整体几何形状引起的部分,但不包括局部焊缝几何形状)。因此,允许的应力值可以更高,但仍大大低于纯材料测试所显示的应力值。
在使用有限元计算时,壳模型通常会,而固体力学模型则会计算应力细节,而这些细节在进行焊接疲劳分析时是不需要的。
推荐方法
有限元模型可能包含奇点的原因很多,并且往往本质不同。例如:
- 正如本文开头提到的博客中所讨论的,边界条件会引起奇点。如果这种奇点给分析带来问题,可以通过完善边界条件来解决。
- 之所以引入尖角,是因为局部几何形状的尺度较小,在全局尺度上建立圆角模型并不合理。在这种情况下,并不存在真正的奇点,而是一个明确定义的应力集中。最精确的方法是使用子建模来确定局部应力状态。在全局模型中,可以利用应力集中附近幂律衰减应力场的振幅了解应力集中的位置。另一种方法是将近场应力场知识与应力场与局部应力集中相关的知识结合起来,从而得出局部应力集中的估计值。
您可以仿照焊接评估的方法,但要因地制宜。要做到这一点,需要有广泛的经验基础。以前的设计哪些失败了,哪些没有失败?然后,您需要对以前的设计进行分析,并尝试找到与经验相关的评估方法。
首先为这些设计建立有限元模型,并尝试确定一个区域,在该区域内的应力或应变场既不受局部缺口几何形状的控制,也不受整体几何形状的控制。至少在制定标准时,可能有必要使用子模型。
使用什么标准通常并不明显。由于您只是要进行相对比较,而不是将计算出的数字与任何物理强度值联系起来,因此有许多可能的选择。例如:
- 数量应易于计算。
- 该数量不应对分析中的不确定性过于灵敏。
- 如果可能,数量应与物理场相关。例如,如果材料是脆性材料,那么查看最大主应力或主应变可能比使用 von Mises 等效应力准则更好。
- 如果疲劳是一个问题,数量必须对逆载荷反灵敏。
- 如果可能,请选择应变准则而不是应力准则。因为应变是直接根据位移计算得出的。应力则是通过应变的组合计算得出的。这表示应变张量中一个不准确的分量将传播到应力张量中的所有元素。
- 在 COMSOL Multiphysics® 软件中,您可以使用 安全 功能来评估大量不同的标准,包括用户定义的标准。
一般情况下,奇点的幂次是未知的。但我们知道,在某一区域,相关量的变化为
K 和 p 的值可以通过最小二乘法拟合或简单地使用应力应变对数-图中直线部分上的两点值来获得。由于 p 必须被看作某类奇点的恒定属性,因此计算出的值可用作方法有效性的检验。
在 p 已知的情况下,应将 K 的值与允许值进行比较。这与断裂力学中处理裂纹的方法类似。
百分比法
另一种获得允许应力水平的方法是将参考应力定义为在参考体积的给定部分(例如 5%)中超出的值。如果该参考应力低于允许值,则该设计被接受。使用这种方法,可以避免计算接近奇点的问题。只需计算出超过参考应力的体积即可,而该体积的边界在距奇点一定距离的地方,此处解可以很好地收敛。
这种方法看似简单,但应用起来却需要一定的标准化。其中一个问题就是如何确定参考体积。如果使用结构的总体积,那么只需在低应力区域添加更多材料就可以降低参考应力,这当然是不合理的。参考体积必须与奇点周围特定区域的大小等因素相关。另一个缺点是,优化方法可能会选择重新定位应力,从而使参考应力减小,而峰值应力增大。
同样,我们也只能对类似结构进行比较来确定。
现在,我们来讨论如何使用百分比法计算应力值。在 COMSOL Multiphysics® 中,无法直接计算 5% 的应力值。下面介绍 3 种替代方法。
方法 1
如果只需要一次求值,最快的方法通常是手动迭代几次。您只需创建一个积分算子(例如,intop1),然后对 intop1(solid.mises>sRef)/intop1(1) 这样的表达式进行求值。通过多次改变参考应力 sRef,很快就能找到与给定百分比相对应的值。
方法 2
使用模型方法自动执行方法 1。
方法 3
您可以设置一个额外的方程,求解应力值,下文将对此进行说明。
待解方程如下:
\sigma_\mathrm{c} 是计算应力。它可能是如 von Mises 的等效应力、第一主应力或其他应力。当然,也可以使用相同的程序来计算应变或能量标准。用 V_\mathrm{ref} 表示参考体积, \beta 为百分比。积分内的布尔表达式假定为 1 时为真,定义为 0 时为假。
为了在计算时更容易处理缩放,最好将方程改写为
可以像第一种方法那样,使用积分算子计算积分。在 COMSOL Multiphysics® 中使用 全局方程 节点实现该方程的直接方法如下所示:
遗憾的是,这样行不通。不等式是不可微的,因此无法形成雅可比矩阵。刚度矩阵将只包含该方程的零点。不过,可以通过手动引入有限差分导数来规避这个问题。该表达式较长,需要您对 COMSOL® 中基于方程的建模有一定的了解,下面的附加信息部分将给出详细解释。
下图所示是一个修改后的全局方程,它可以解决如何找到能给出预期百分比的应力的问题。
这里,用户定义的参数 dS 是应力增量,在附加信息部分用 \Delta \sigma 表示。
我们以上文的缺口板为例来说明这种方法。由于参考体积应与板的尺寸无关,可以在缺口周围选择一个圆。在这种情况下,圆的半径可以根据结构的以下特征长度来选择:
- 宽度: 1 m
- 最小裂缝长度: 0.1 m
- 最小韧带宽度: 0.3 m
- 最大切口半径: 0.01 m
基于缺口尖端周围半径为 0.05 m 的圆确定的参考体积将远离结构的边界,但也将远离缺口本身的细节。

在不同的狭缝深度和切口半径下,5% 的参考体积所超出的应力水平。
对于所有狭缝深度值,5% 应力基本上与切口半径无关。它只对切口深度敏感。这与基本原理是一致的:避免对局部(可能是奇异的)应力场细节的灵敏性。无论使用尖角还是圆角,都能得到相同的结果。从本质上讲,这种方法提供的信息与应力强度因子相同:它测量的是奇点的强度。如果对具有相同圆角类型的结构进行比较,这种方法可以成为应力奇点处理的标准。
附加信息
该表达式包含两个项:第一个项产生残差,第二个项产生雅可比矩阵。这是一种通常可用于高级建模的解决方案。例如,如果创建精确的雅可比函数成本较高,则可以使用类似的表达式将正确的残差与近似的雅可比函数结合起来。
在多个地方使用 nojac(expr) 算子,用于确保不产生给定表达式的雅可比贡献。
雅可比项乘以系数 (sRef-nojac(sRef))。由于这个表达式的求值总是为零,因此这部分表达式不会产生残差。 sRef 相对于自身的导数就是 1,而表达式的剩余部分就是导数的对称有限差分表达式。
式中,\Delta \sigma 是应力的有限变化,应选择尽可能小的变化量,同时还要保证 \displaystyle \int_V (\sigma_\mathrm{ref}+\Delta \sigma<\sigma_\mathrm{c}) \;dV 计算出的体积与 \displaystyle \int_V (\sigma_\mathrm{ref}<\sigma_\mathrm{c}) \; dV 有明显差异。一个好的水平是,当一个单元上的应力变化在等值面附近为时,将得出参考应力 \sigma_\mathrm{ref}。
结束语
尽管从理论上讲,不可能对奇点处的梯度和通量(应变和应力)进行计算,但还是有一些系统的方法可以解决这个问题。不过,这些方法需要有足够的实验数据来解释所选择的临界量。
点击下面的按钮,下载本文中使用的模型。





评论 (0)