
有限元模型有时会遇到奇点问题,即解在某些点上表现出趋向无穷大的特性。这篇博客,我们将探讨这些奇点出现的常见原因,提出有效的消除策略,并讨论当模型中存在奇点时,如何准确解读和分析结果。尽管本文的讨论主要集中在结构力学领域,但所探讨的奇点现象及其处理方法同样适用于其他物理场。
问题
我在从事结构分析咨询师工作时,有时会遇到这样的问题:如何向客户解释有限元模型中出现的异常高的应力峰值?对于经验丰富的分析师而言,他们清楚哪些应力峰值是建模过程中的预期效应,因此可以忽略不计。但是,一旦项目要求“应力在任何位置都不得超过屈服应力的70%”,这一问题就必须重视。同样重要的是,彩色仿真图中的小红点也不容忽视。因此,我们必须具备能够合理解释模型结果的能力。
尖角:奇点的原型
尖角会导致所有椭圆型偏微分方程的因变量导数具有奇异性。在结构力学中,这代表应变可以无穷大,因为自由度是位移。除非受到材料模型的限制,否则,在这种情况下应力也将无穷大。
在大多数结构力学分析中,人们更关注应力。这就是为什么在结构力学中,奇异性问题比其他大多数物理更为突出。例如,在传热分析中,相较于热通量的局部值(在这些区域,奇异点也许更明显),我们可能更多关注温度。
让我们来看一个奇点的原型问题。下图是一块 2 m x 1 m 的矩形板,该矩形板的侧面有一个仅受张力作用的边长为 0.2 m 的正方形切口:
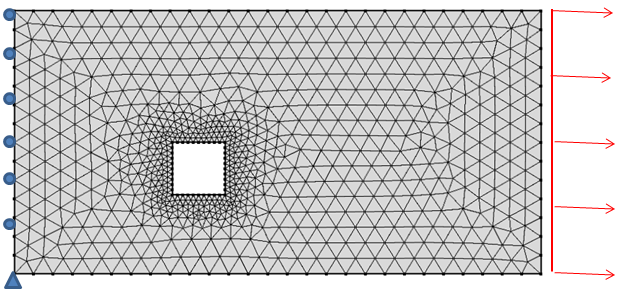
该矩形板左边受到约束,右边承受均匀的载荷。
当在切口周围绘制两种不同的网格时,等效应力的默认图表会呈现出截然不同的结果。由于在包含较细网格的模型中,峰值应力是较粗网格的两倍高,因此导致应力场中的大多数细节信息丢失。当然,我们可以通过手动调整绘图的范围来补救,但这样做可能会在一开始掩盖一些重要的细节。
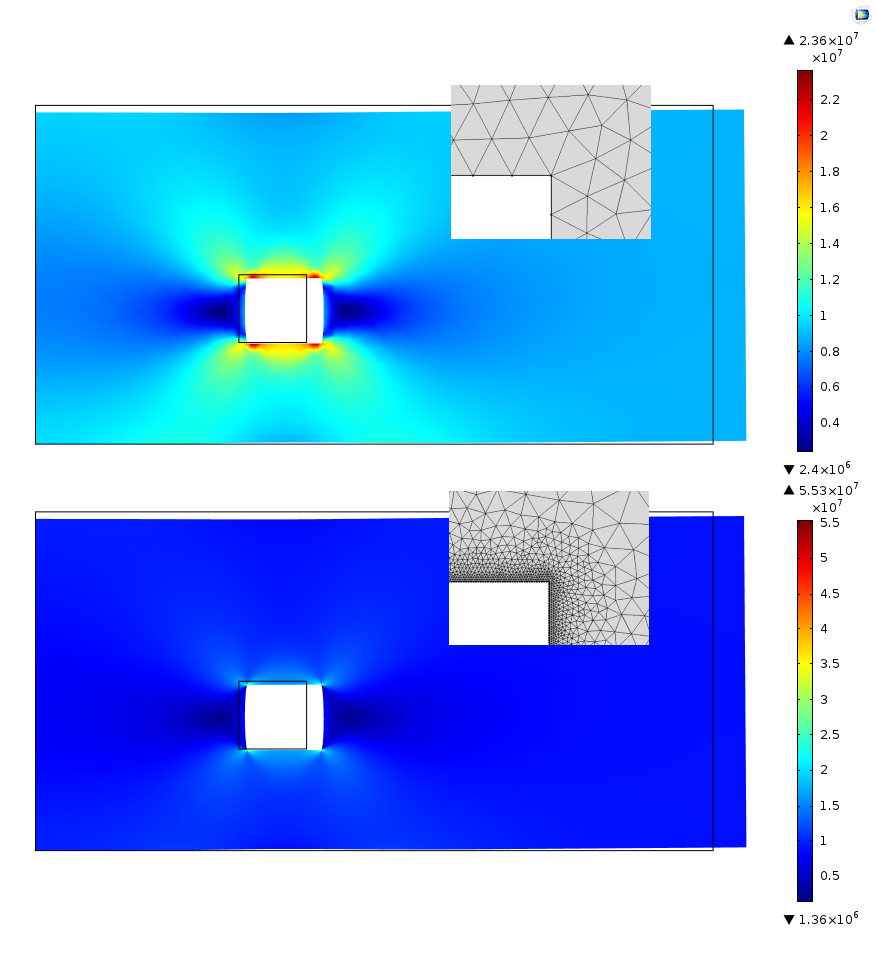
两幅绘图中的等效应力场相同。这两幅图均按照与网格有关的峰值应力被自动缩放。
实际上,拐角处使用的网格单元越小,检测到的应力值就越高。由于“真实的”解趋于无穷大,因此计算结果将不会收敛。
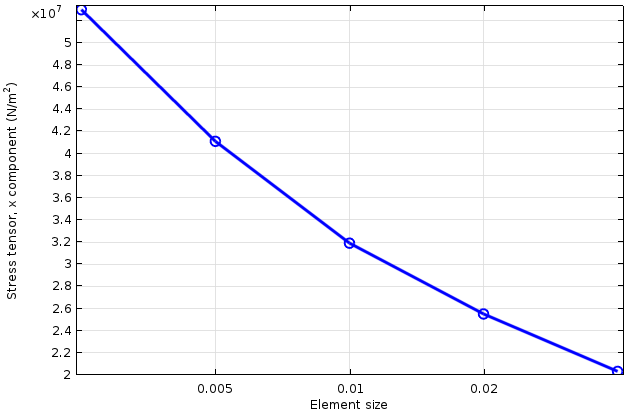
拐角处的应力是网格单元大小(对数横轴)的函数。
如果我们研究切口附近的应力场,会发现应力峰值呈现出高度的局部化特性。下图显示了离切口0.05 m处,垂直切线上绘制的应力分布图。在这个距离下,即使拐角处的峰值应力变化了两倍,此处的应力几乎保持不变。
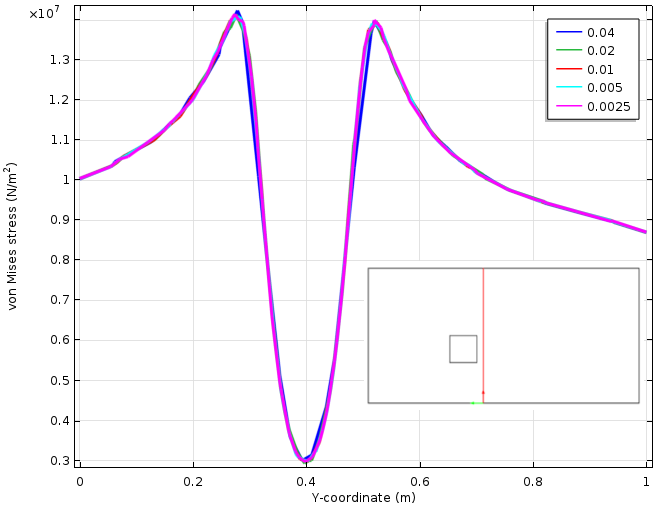
沿切线的应力变化(以红色表示)。使用了五种不同的网格大小。
事实上,在实际生活中,很少有完美的尖角。因此,有人可能会说,通过使用包含所有圆角的精确几何图形表示,理论上可以避免奇点,但这需要很大的代价。如果网格必须解析非常小的几何细节,那么模型的大小将急剧增加(尤其是在 3D 情况下)。即使可以使用完美的 CAD 几何图形,通常也要去除几何图形在分析范围内不重要的小细节。因此,在多数情况下,我们会在预处理阶段有意地引入尖角。
但是,保留尖角的做法也存在一些不足:
- 如果材料模型是非线性的,那么奇点处可能存在数值问题。例如,蠕变模型预测的应变率通常与应力的高次幂成正比。奇点处的高应力(仅由网格确定的值)升高到 5 的幂次方可能会导致应变率非常高,迫使时间步长缩短至毫秒级别,而实际上我们可能希望研究的是持续数月的事件。如果仍要保留尖角,此处的补救方法是将奇点封闭在较小的弹性域中。
- 由于奇点将主导整个解的其余部分,因此自适应网格划分、误差估计等方法可能会失效。在进行这些操作时,应排除尖角区域。
- 当将应力作为问题表述的一部分进行优化时,奇点将仅在减小非物理峰值应力大小上产生最优解。在支架的多约束优化教程中,用螺栓固定的支架区域被排除在寻找最大应力的搜索范围之外。
- 如前所述,高应力峰值往往会在视觉和心理上掩盖解中一些有趣的特征。
从物理学的角度讲,如果拐角非常尖锐,高应变将损坏材料。脆性材料可能会开裂,韧性材料可能会屈服。虽然这听起来可能令人震惊,但是在大多数情况下,这种损坏只会引起应力在局部重新分布。从周边结构的角度来看,其效果并不比在一定程度上改变圆角半径更显著。如果载荷是周期性的,那么高局部应力将是一个真正的问题,它会造成疲劳风险。
在建筑物中,没有人担心窗户开口是带尖角的矩形。但是,在一架飞机上,你会发现它使用了平滑的圆角窗口,因为机舱内压力与外界压力之间的变化将产生周期性应力。


左图:有尖角的矩形窗口。图片由 Jose Mario Pires 提供。通过 Wikimedia Commons共享,获 CC BY-SA 4.0 许可。右图:有平滑圆角的窗口。图片由 Orin Zebest 提供。通过 Wikimedia Commons共享,获 CC BY-SA 2.0 许可。
实际上,许多设计标准都承认,在静态载荷条件下,允许存在较高的局部应力,因为这类应力并不会影响结构的承载能力。使用这种方法需要对应力场进行系统的分类。例如,ASME Boiler & Pressure Vessel Code 中就描述了此类方法。
另一方面,对于周期性载荷,获得非常精确的应力值很重要,因为疲劳寿命在很大程度上取决于应力大小。在这种情况下,不仅在几何方面,在网格分辨率方面精确地表示圆角也很重要。如果模型太大无法处理,可以使用子模型,这篇博客:如何在大型模型中分析局部效应对此方法进行了详细的介绍。

右图中精确子模型的输入为全局分析的结果。
提示:如果想进一步探索子模型技术,您可以从 COMSOL 案例下载库中下载轮毂子模型分析教程模型进行学习。
点荷载
施加到实体上单个点的力将在局部产生无限大的应力。这是弹性理论中的经典 Boussinesq-Cerruti 问题,其中应力变化与距加载点的距离成反比。
在真实世界中,不存在点载荷,力始终分布在特定区域。从有限元分析的角度来看,问题在于是否值得费力求解这一小区域?圣维南原理 给出了答案:在与载荷区域大小相比足够远的距离处,所有静态等效载荷产生的应力是相同的。
因此,当精确结果在一定距离内不重要时,例如距离加载区域三倍大的地方,只要施加的合力和力矩正确,所施加的载荷实际上对结果的影响不大。就像拐角处的奇点一样,可能仍然需要避免奇点应力的影响。请注意,线荷载与点荷载在引起局部极值应力方面具有相同的效果。
值得一提的是,施加在梁单元或垂直于壳体的点载荷 不会 引起奇点,因为结构单元的弯曲遵循不同于固体力学的方程。但是,在壳平面上施加的点载荷将导致奇点。
约束条件
如果根据施加反作用力的能力来考虑约束,很明显可以得出与载荷有关的相同结论,例如施加到点上的约束。但这还不是全部,下面我们以一个看似对称的约束问题为例来说明。假设有一块板,在其一侧施加恒定的拉伸载荷,而在另一侧施加相应的辊支承约束。
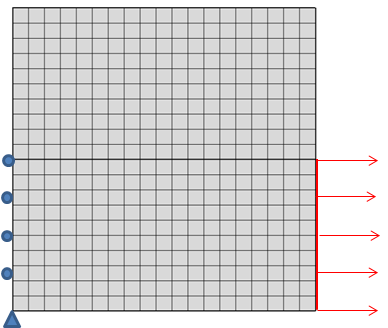
带一半垂直边界约束和载荷的正方形板。
当查看应力分布时,会很明显地发现,辊支承约束的末端会引入奇异性,而载荷的突然变化则不会引入。一个常规的解释是由于约束的末端存在类似于尖角的效应。
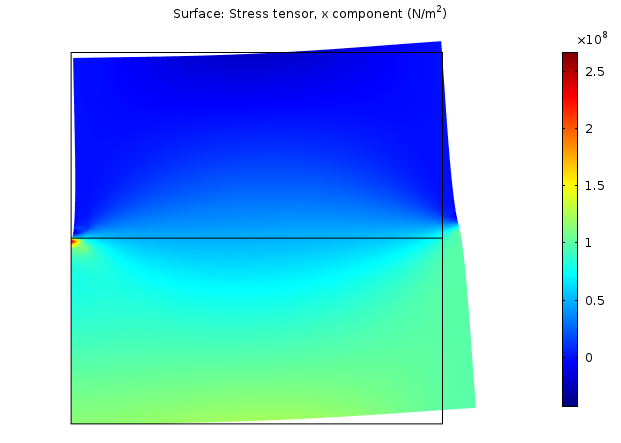
水平应力分布。
实际上,不存在支撑该结构的无限刚性环境。结构分析师此时再一次面临选择:我可以忍受仿真图上这个小小的红点吗?还是需要更多注意结构之外的因素?
如果边界条件引起的奇异性不可接受,则可以考虑以下方法:
- 扩展模型,将因边界条件引起的任何奇点移至关注区域之外。
- 定义一个较柔性的边界条件,例如,应用弹簧基础条件。
- 在扩展计算域时,使用更省时的无限元方法。您可以通过黏土层上的柔性和光滑条形基础教程模型了解更多信息。
在许多类型的转换中,有很多与上述情况相似的不可避免的情况。例如,将刚性域连接到柔性域。
焊缝
焊缝分析非常重要,而且复杂,因此我们可能需要专门发表一篇博客来说明。这里,我们对这个主题仅做简要讨论。
焊接结构通常由薄板组成,因此在这种情况下,我们很自然的想到了壳模型。以下图中的示例模型为例来说明。在这个示例中,小板焊接至宽板的位置明显存在应力集中现象。
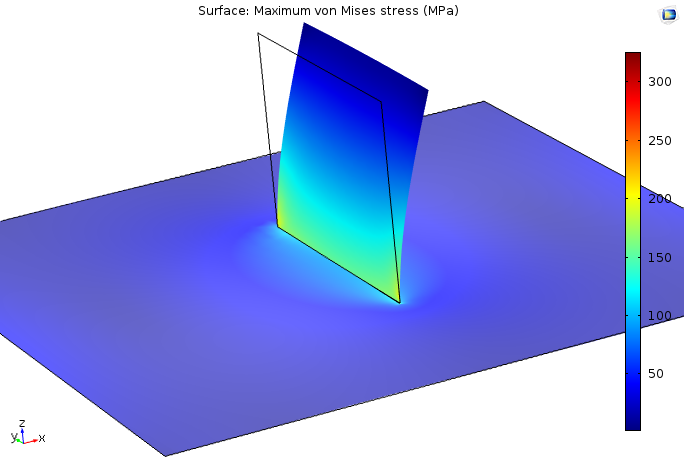
一个简单的壳模型(焊接在一起的两块板)中的应力。
在这个模型中,几何形状和载荷沿几何中心对称。对该模型的网格进行设计,以使焊缝末端的网格更加精细。沿着焊接线的应力图显示了两块板的应力场具有奇异性。
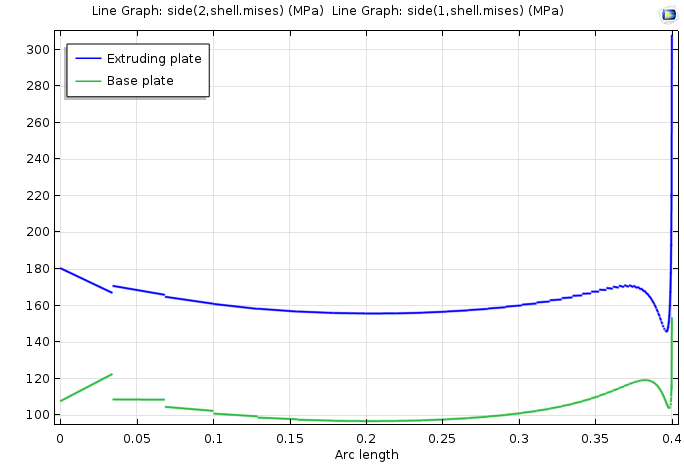
识别奇点的应力图。
对于例如船体、货物起重机和卡车车架等许多焊接结构而言,确定抗疲劳尺寸非常重要。使用固体模型来完善模拟过程并不是常用的方法,除非该结构已经打磨并用 X 射线检查过,否则很少能明确定义焊缝的局部几何形状和质量。焊缝的局部几何形状与两个板的焊缝之间几何形状不一致,但理论上应该相同。
在分析焊缝时,最常用的方法是先将一定距离处沿焊缝线或平行线的应力平均化。对于这种情况,COMSOL Multiphysics 中的截线特别有用,局部坐标系也很方便,因为需要区别对待平行于焊缝和垂直于焊缝的应力分量。然后,再将这些平均应力与用于不同焊接配置和焊接质量的参考值进行比较。如果想了解更多信息,请参阅 Eurocode 3: Design of steel structures — Part 1-9: Fatigue部分的内容。
裂纹
还有一种可能出现的最严重的几何奇点是由裂纹引起的。裂纹可以看作是 180° 凹角,因此处理拐角奇点的许多方法也适用于此。当裂纹存在于有限元模型中时,通常是研究中的重点区域。

裂纹尖端附近的应力场,变形按比例计算。
至少在某些假设下,对于线弹性和弹塑性,从解析解中可以知道裂纹尖端周围的应力场。然而,由于奇点的存在,通过有限元分析计算应力场可能很困难。幸运的是,我们通常不必研究裂纹尖端的细节。例如,在确定应力强度因子时,可以使用J 积分或能释放率 方法。这些方法使用的的是距离裂纹尖端较远的全局量,因此奇点处的细节便不再重要。
提示:您希望进一步探讨J积分方法的使用吗?请参阅 COMSOL 案例库中的单边裂纹教程模型。
结论
在许多有限元模型中,奇点的出现往往由多种因素导致。只要掌握了解读结果和规避潜在影响的方法,这些奇点就不会对模拟造成太大困扰。实际上,许多工业规模的模型都需要有意使用奇点来优化模型。为了减小模型大小和缩短分析时间,通常需要以引入奇点的方式来简化几何细节、载荷和边界条件。






评论 (0)