
最近在 Youtube 上,Stand-up Maths 频道发布了一段讨论跳环问题的视频。虽然这个问题看起来很简单,但其中涉及的物理学和数学在过去半个世纪中曾引起了许多研究人员的兴趣。在这篇博客中,我们将介绍一些可以帮助解跳环物理原理的模型。
问题
这个问题最初的描述是:一个理想的、无质量的刚性的环,在其周长上附加一个单点质量。如果环沿水平面滚动,这个点质量是否有可能脱离该平面并跳到空中?运动开始时,环处于不稳定的平衡位置,点质量位于最高点。
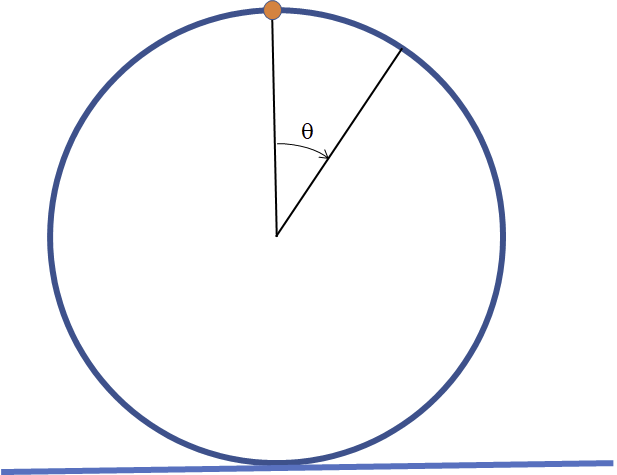
本文我们来看一个与视频中讨论的环类似的环,稍微做了一些修改。例如,这个环不再是无质量的,而是有一个均匀分布的质量。该系统的总质量是 m,其中 \gamma m 是分配给点质量的部分,剩下的总质量 (1-\gamma)m 分布在环的周围。使用特殊情况 \gamma = 1,然后恢复原始配置。确切的物理特性在这里并不重要,但可以作为参考:环的半径是 R = 1 \ m,总质量是 m = 1 \text{kg},质量分布参数 \gamma = 3/4。环和平面之间的摩擦系数被设定为 \mu = 1。
在几何中,有几个不同的地方可以测量速度。除非有其他说明,速度(v)是指环中心的速度。在纯滚动运动中,它与角速度的关系为 v = R \dot \theta。
第一次尝试
为了更好地熟悉这个问题,我们首先在低速下滚动环。使用多体动力学 接口中的一个刚体来模拟环。使用刚体接触 功能模拟环和平面之间的连接。
参考配置(零旋转时)是当点质量位于环的顶部时。如果只给环一个最小的推力(在这种情况下,初始速度为 {v}_{\textsl 0}= 0.1 \ m/s),开始的旋转将非常缓慢,但随着点质量垂直位置的下降,旋转速度增加。一圈旋转的速度变化很大,当点质量再次到达顶部时,环几乎达到了静止状态。请看下面的动画。
环的颜色是由速度决定的。黑色轨迹显示了点质量(摆线)的路径。绿色轨迹显示了系统重心的路径。箭头与接触力成正比。
让我们更详细地研究一些关键特征。首先,绘制速度图。用角速度乘以环半径,这样就可以直接与中心的平移速度进行比较。只要运动是纯旋转,这两条曲线就会重合。
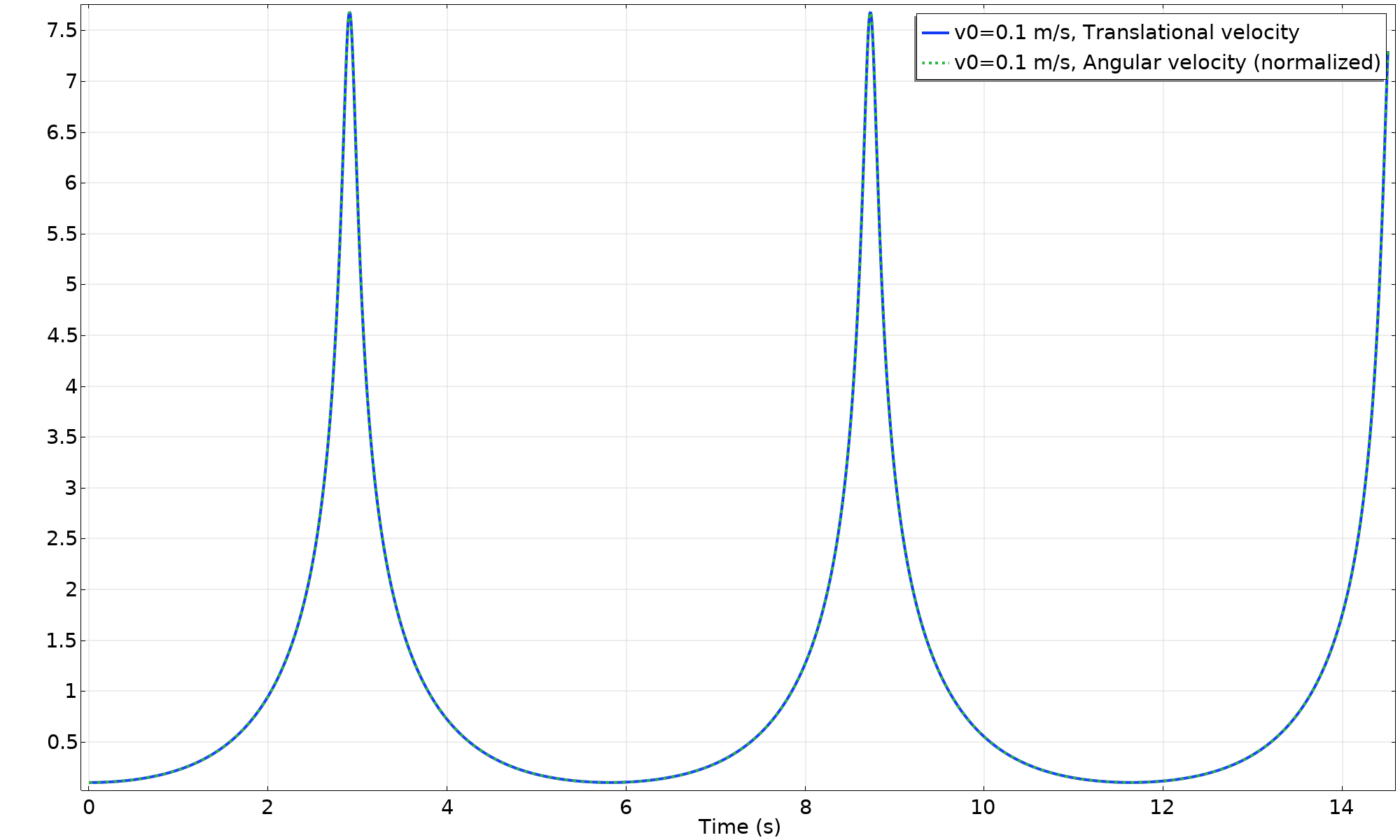
速度与时间的关系图。
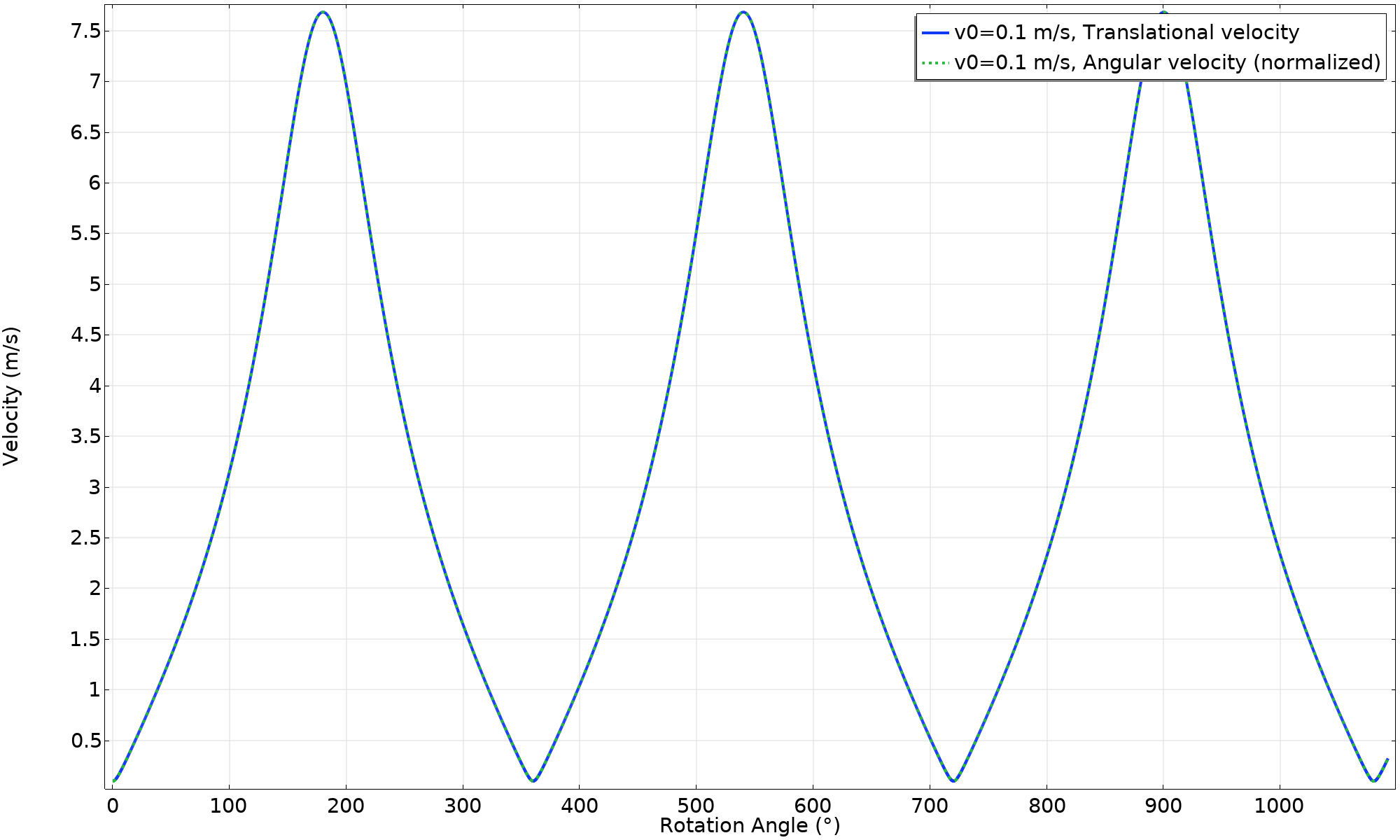
速度与旋转角度的关系图。
点质量的势能可以被认为是旋转的驱动力。圆环本身的质量不会改变圆环离地面的高度,除非圆环刚好在跳动,所以如果圆环只是滚动,这部分质量不会对势能做出贡献。
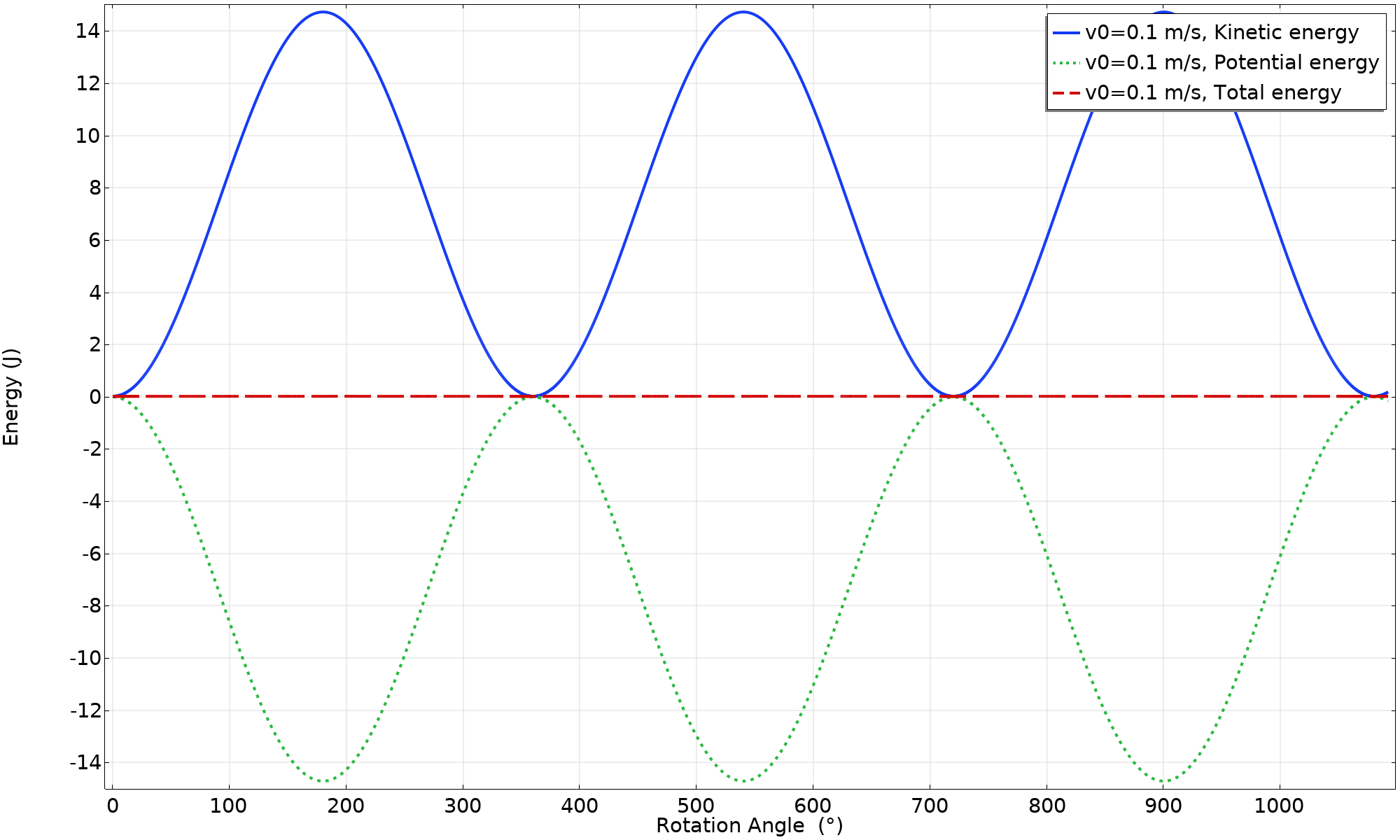
系统的势能和动能。
当绘制角度图时,能量转换作为纯谐波函数变化。这是点质量的垂直位置的直接结果。
我们将对这个理论做一点稍微的改变,最后有一个有趣的转折。
系统的势能只受质点垂直位置的影响,可以写成:
参考高度的选择是为了使质点到达其顶部位置时势能为零。
通过一些包括重心位置和速度的代数转换,动能可以写成:
得到两种能量的表达式后,可以用能量守恒原则来推导角速度与旋转角度的函数的闭合表达式:
插入动能和势能的表达式,得到:
因此,角度与角速度的函数关系为:
最大角速度必须发生在 \theta = \pi:
\sqrt{ \frac{2\gamma g R + v_0^2(1+\gamma)}{1-\gamma}}
请注意,当 \gamma 接近 1 时,会发生什么情况(原来只有一个点质量的问题)。最大角速度接近无穷大!这听起来非常不符合物理学!
问题是,在滚动运动中,环和地板的接触点总是处于静止状态。当所有的质量都在这个点时,动能为零。同时,动能应该等于损失的势能。这并不相加!另外,正如这个问题的原作者 John Littlewood 在他的 A Mathematicians Miscellany 一书中所说的,当 \theta = 90° 时,应该已经有了跳跃运动。
无论如何,这在现实中不会发生。为了获得高速度,需要非常大的加速度。因此,对于任何有限的摩擦系数值,迟早都会出现滑动。
最后,让我们看一下接触力。
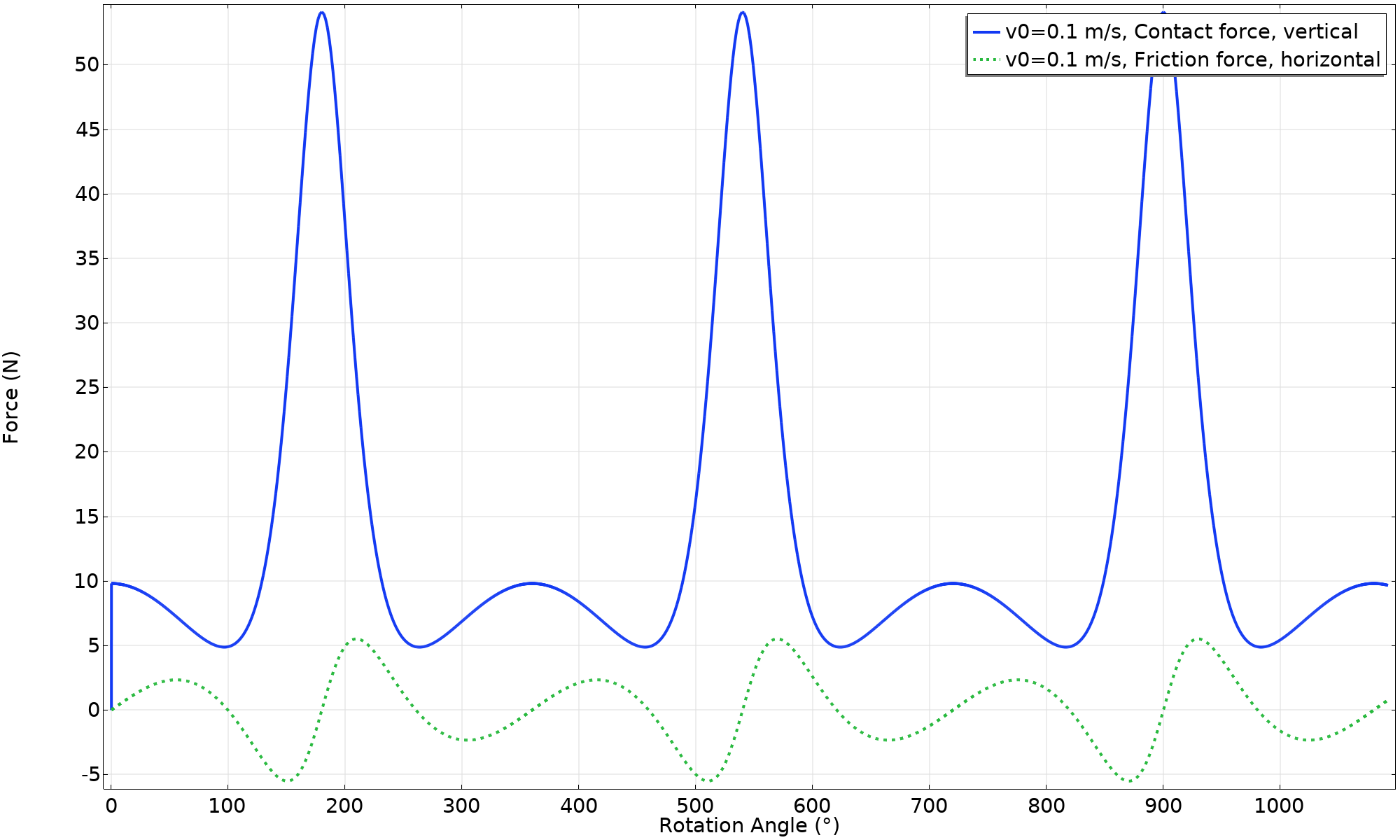
作用在环上的接触力。
由摩擦引起的水平力,是驱动环加速和减速的原因。要获得这个动画所预测的纯滚动运动,要求具备两个条件:
- 垂直接触力必须始终是正的(F_{\text n} > 0)。如果 F_{\text n}= 0,则环形物与表面失去接触。
- 水平摩擦力不能超过库仑摩擦定律所允许的范围(|F_{\text f}| < μ F \text {n})。如果发生这种情况,就会出现打滑现象。
检查摩擦力标准的一个简单方法是绘制 F_{\text f}/ μ F \text{n}。在这种情况下,幅度很大;只有大约 38% 的可用摩擦力被利用。另一种解释,至少 0.38 的摩擦系数对维持纯滚动运动是必要的。
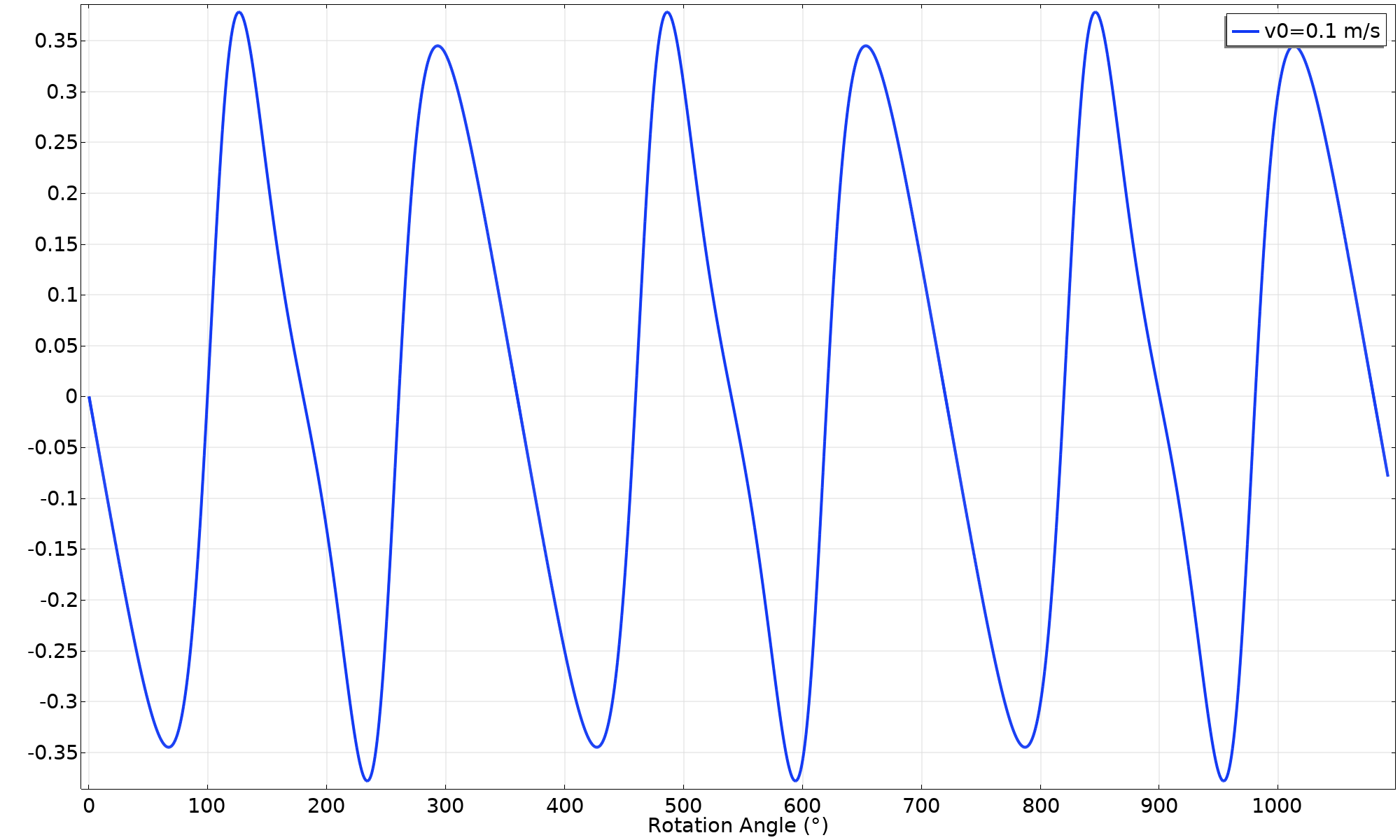
摩擦力利用系数。
提高速度
在第二次尝试中,我们给了环一个更高的初始速度 (v_ \textsl{0} = 2 \ \text {m/s})。如下图所示,仍然有一个纯滚动运动。但是结果发生了一些有趣的变化,例如:
- 速度更高,但更均匀。
- 最小的接触力已经下降。原因是,随着旋转速度的提高,质点的离心力增加。因此,当位置和速度的组合合适时,就会有一个很大的垂直力,抵消了环的自重。
- 可用的摩擦力被使用的部分更多。这是由于较低的接触力和较高的反作用力相结合,平衡了惯性力。
运动的动画(v_ \textsl {0}= 2 \ \text{m/s})。
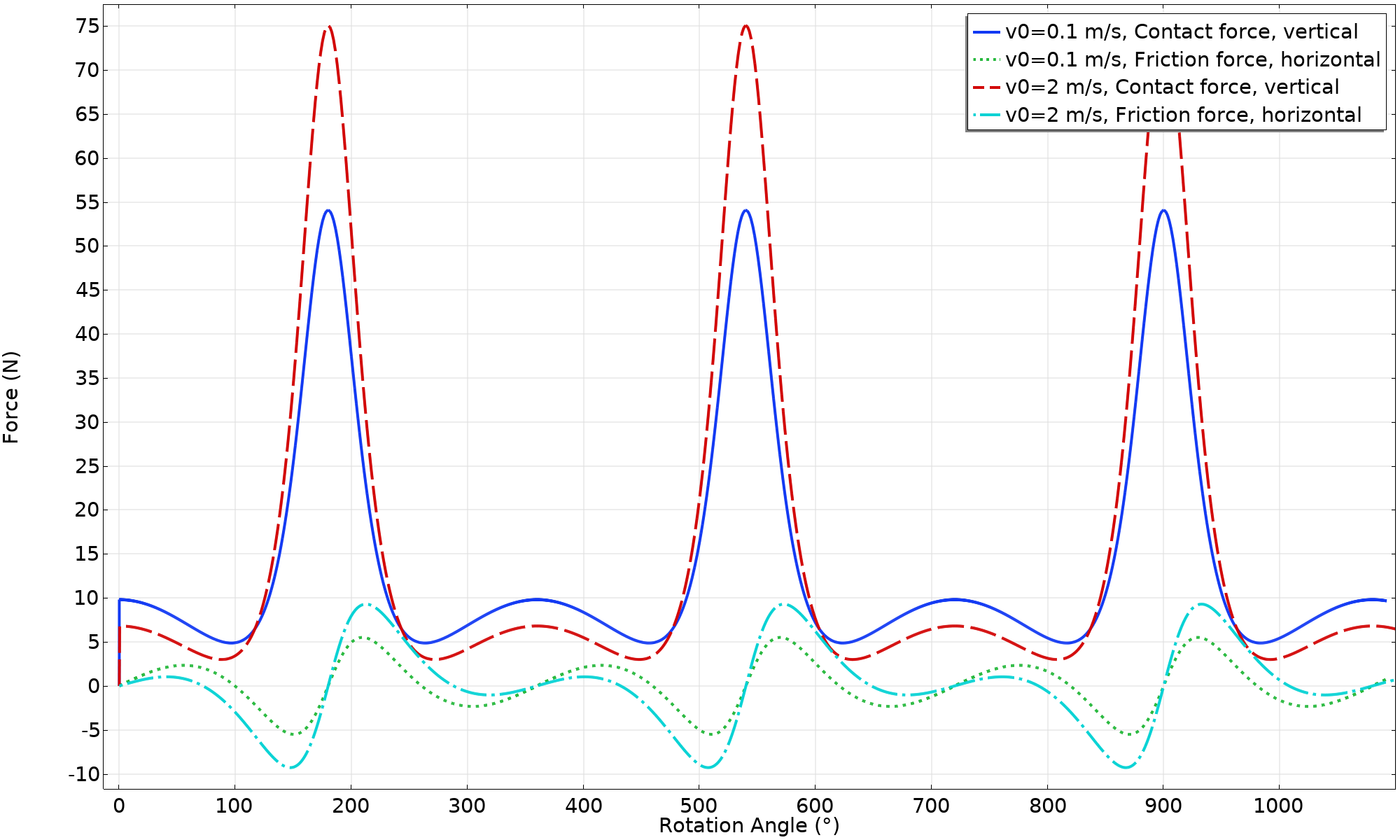
作用在环上的接触力(v_ \textsl {0} = 2 \ \text {m/s})。
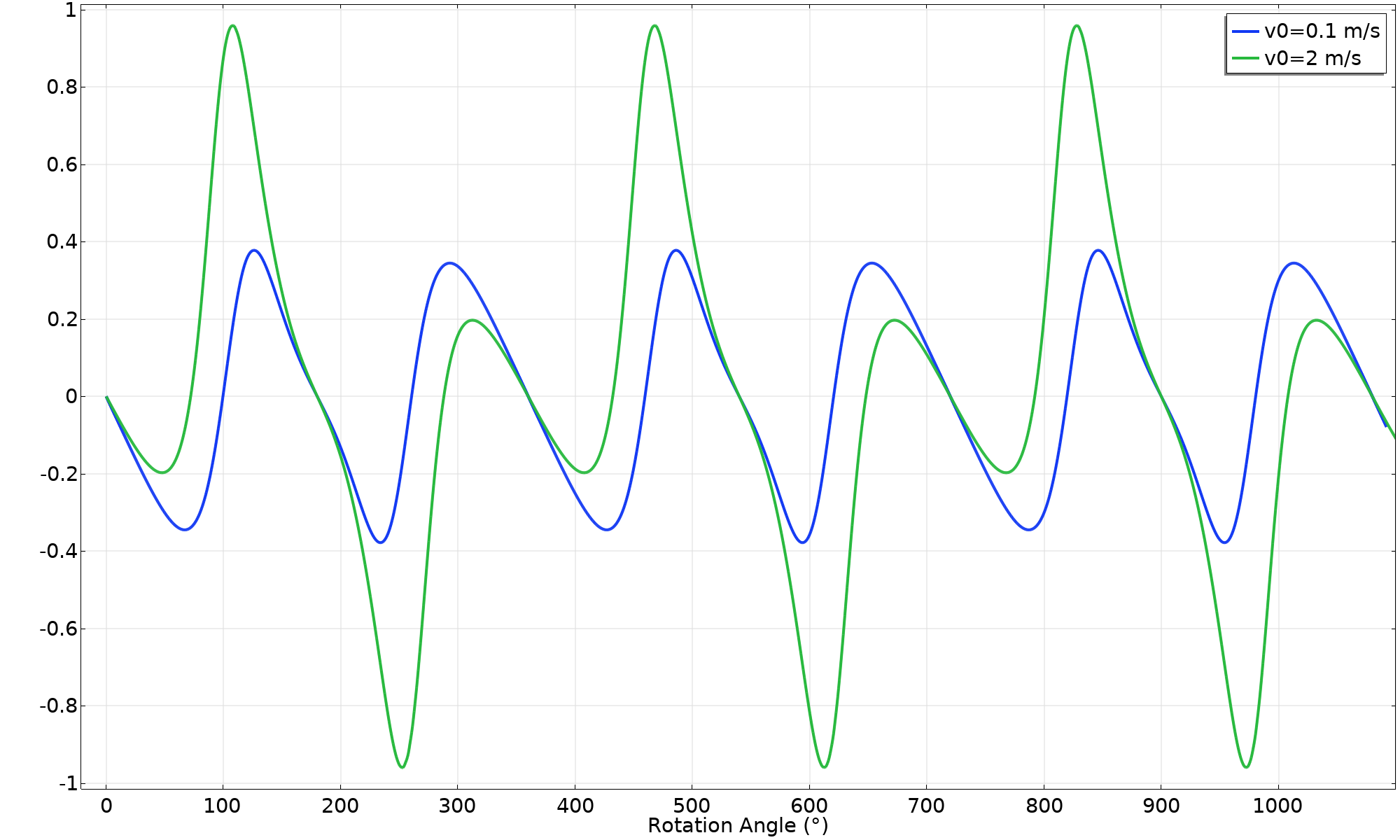
摩擦力利用系数 (v_ \textsl{0} = 2 \ \text {m/s})。
如果我们把这些点连接起来,很明显,在某个稍高的初始速度下,环和水平面之间会发生滑移。在接下来的尝试中,使用 v_ \textsl {0}= 2.8 \ \text{m/s}。现在我们可以看到,摩擦利用系数趋于 1,这意味着出现了滑动。这从动画中不太容易确定,但速度图表明平移速度和角速度不再是相同的。
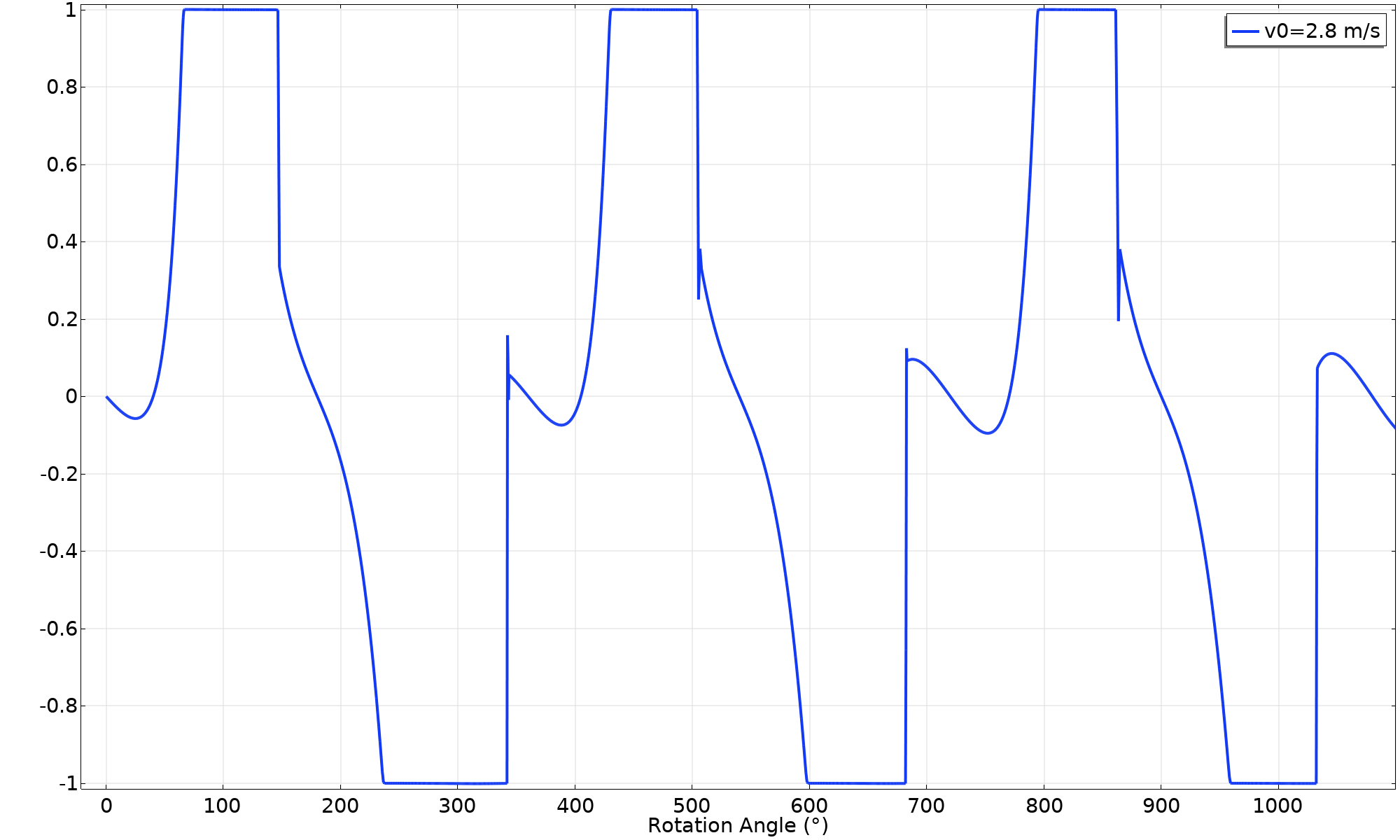
摩擦力利用系数(v_ \textsl {0} = 2.8 \ \text {m/s})。
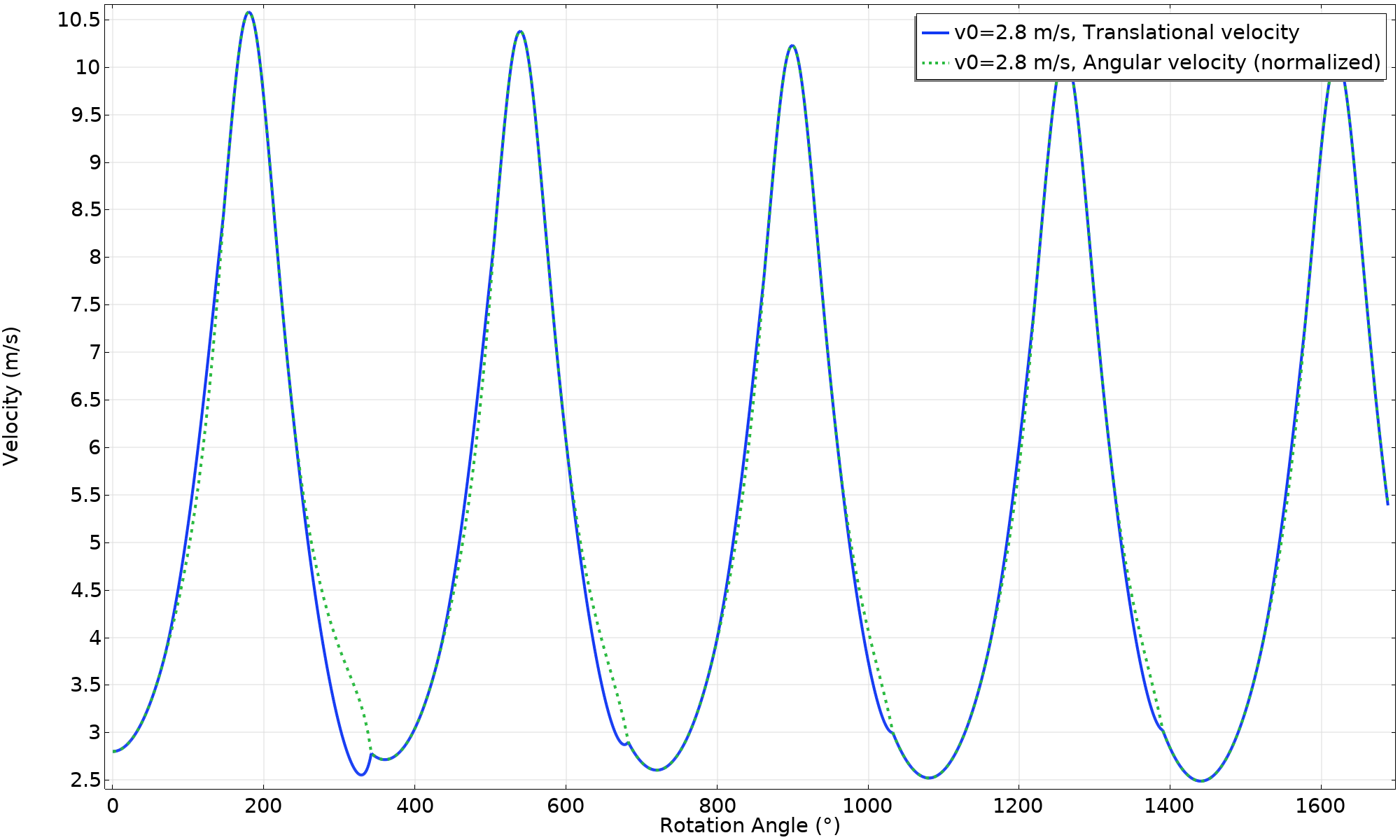
速度(v_ \textsl{0} = 2.8 \ \text {m/s})。
可以看出,每个周期的速度峰值都在下降。如果我们继续模拟,它将以纯滚动运动结束(一旦有足够的能量被耗散)。下面是能量平衡图。“总”能量被定义为势能和动能之和。
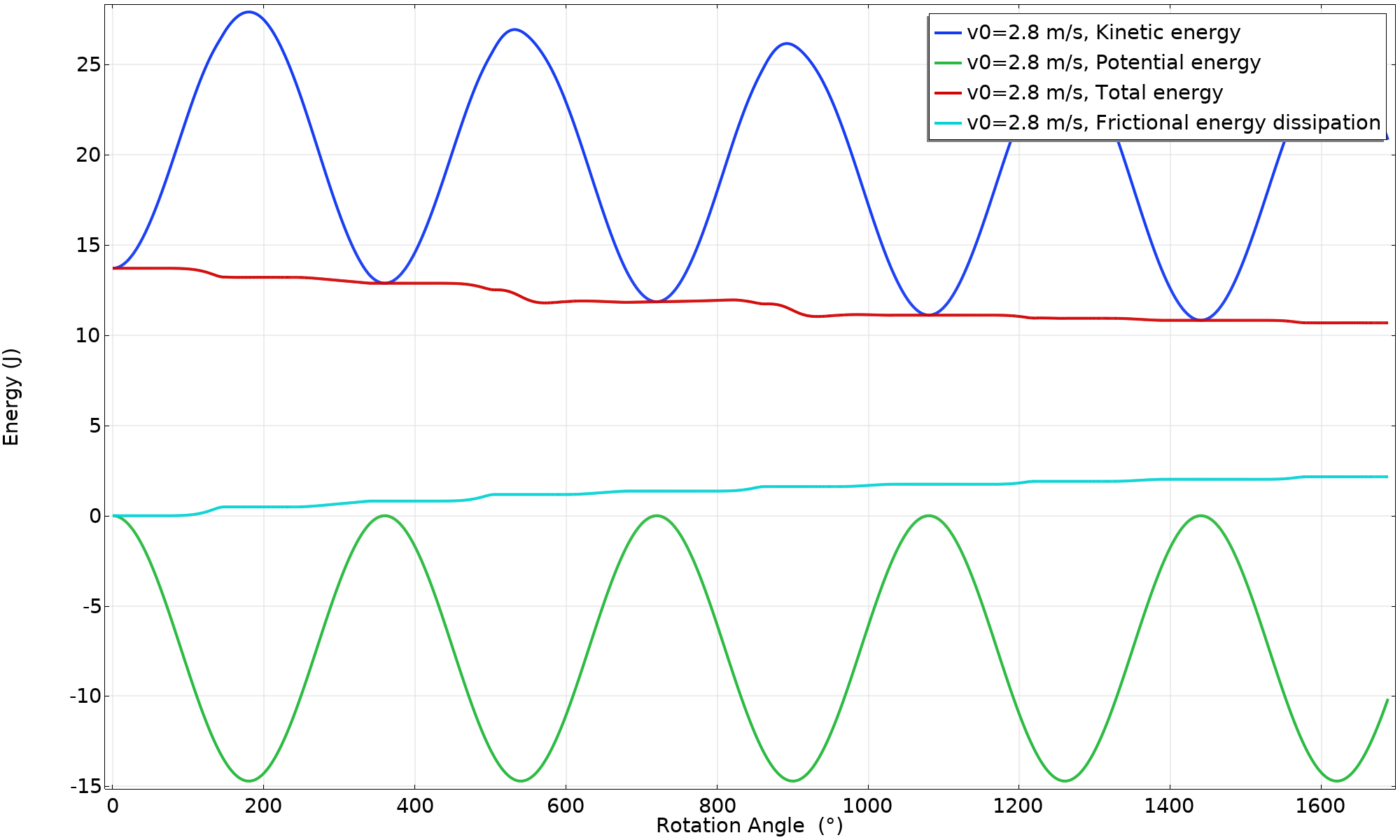
能量平衡(v_ \textsl {0}= 2.8 \ \text{m/s})。
跳跃的环!
将初始速度增加到 3.1m/s 后,动画变得非常有趣!
运动的动画 (v_ \textsl {0} = 3.1 \ \text {m/s})。
在上面的动画中,跳环在完成一个完整的旋转之前就出现了跳跃。正如预测的那样,这就是在 YouTube 视频中显示的相位图的右上角。在这副图中,当环在空中时,重心的轨迹被染成红色。曲线的这一部分形成了一个抛物线运动。
速度图显示,当环飞行时,角速度是恒定的。它必须是恒定的,因为没有施加外部力矩。不太直观能看出的是,即使没有力,速度也不是恒定的。为什么呢?
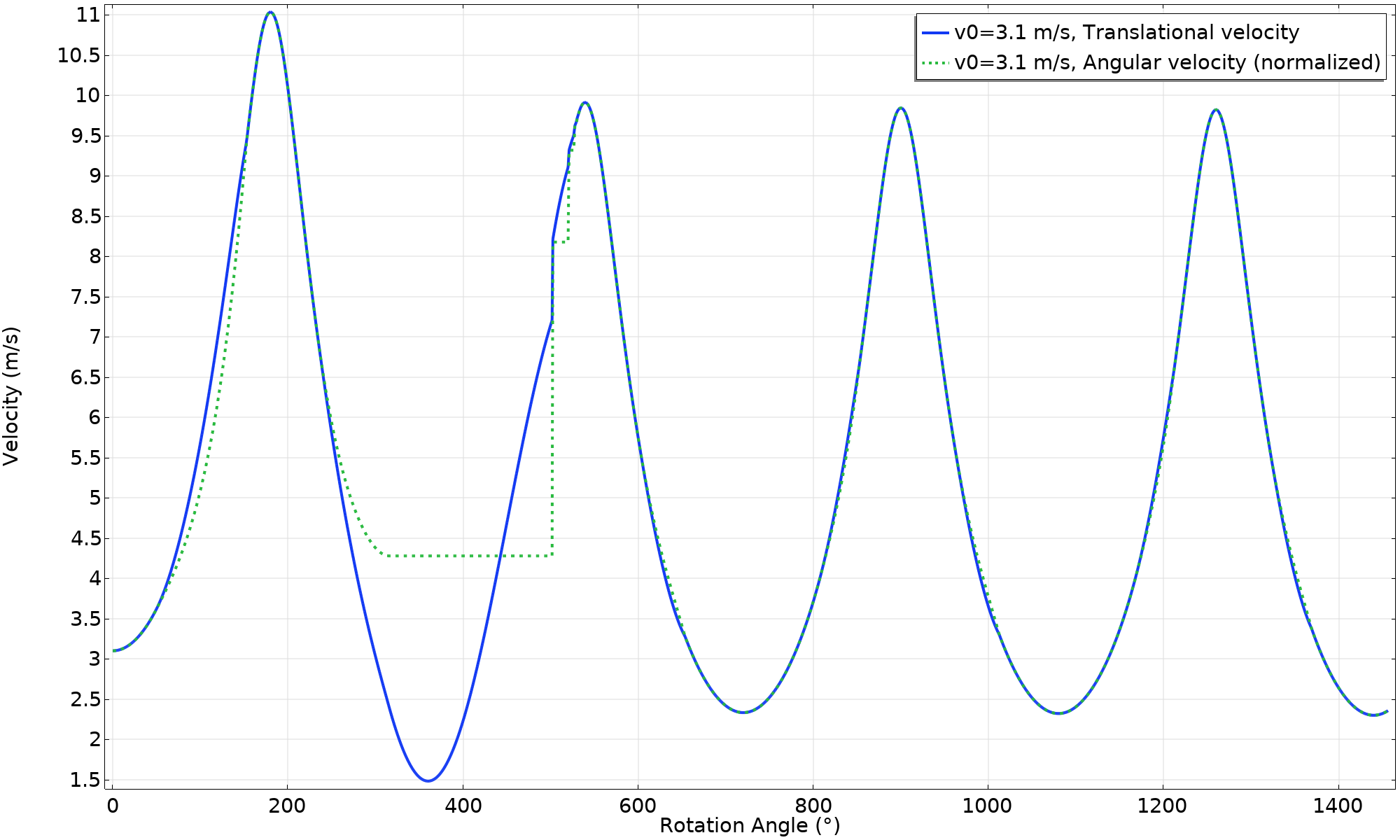
速度(v_ \textsl{0} = 3.1 \ \text {m/s})。
那么,正在绘制的速度是环形中心的速度,而重力中心的速度是恒定的,重力中心实际上围绕环形中心旋转。
能量平衡图给出了进一步的见解。
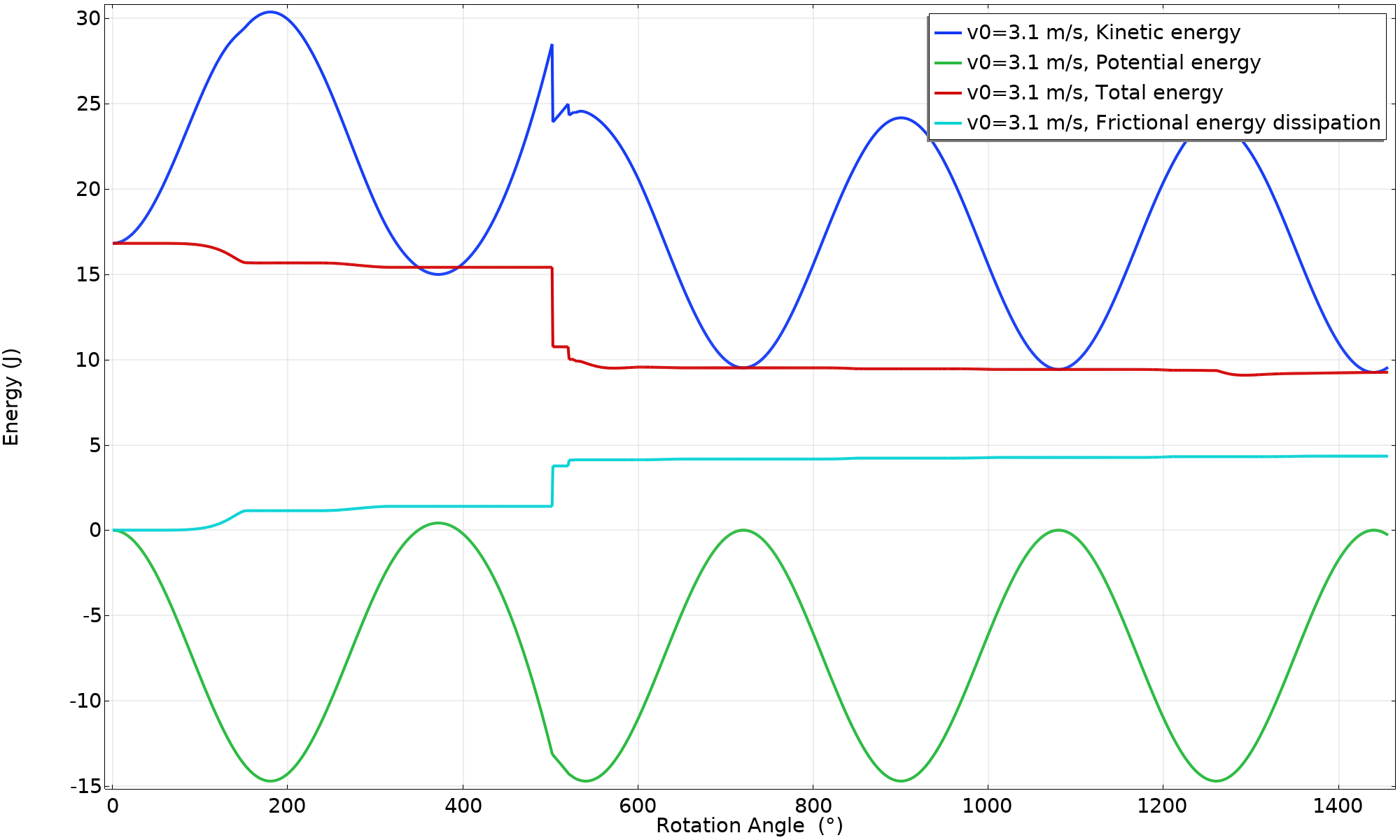
能量平衡 (v_ \textsl {0}= 3.1 \ \text{m/s})。
请注意,在 350° 和 395° 之间的短时间内,势能略大于零,导致总能量大于动能。这是由于环的中心向上移动的影响。图中使用的势能表达式是基于实际位置,而不是基于上述的表达式 W_p,其中假定了滚动。
在这个模拟中,落地后有一个纯滚动运动。然而,这个结果是不可信的。如果你仔细观察,可以看到在撞击过程中损失的能量明显大于同一时刻的摩擦损失。这两种损失机制都将与接触条件的数值模型密切相关。我们没有足够的数据来说明两个刚性物体之间的碰撞过程中应该发生什么。
重新审视低摩擦率
在最初的尝试中,摩擦系数大约低于 \mu = 0.4 时,会导致滑动,即使初始速度很低。为了查看会发生什么,我们用 \mu = 0.3 来尝试。
运动的动画(v_{0} = 0.1 \ m/s, \mu = 0.3)。
由于存在滑动,能量被耗散了。系统中没有足够的动能来提升质点回到顶部位置。轮子开始向相反方向滚动,然后来回摇晃。从速度和能量图中可以看出,较低的摩擦力值诱发了几次滑动。由于运动相对于角度来说不是单调的,我们绘制了这种情况下,数量与时间的关系图。
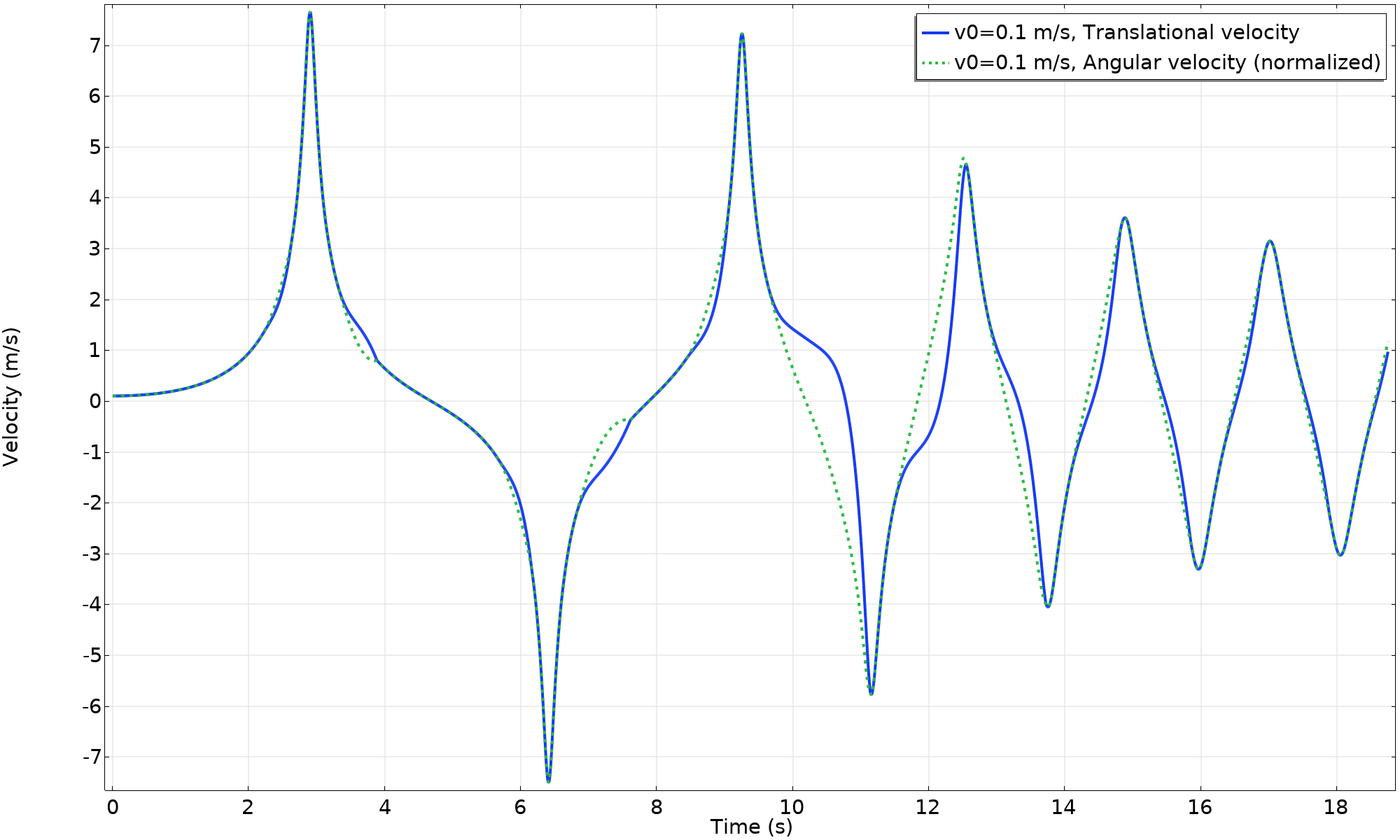
速度 (v_{0} = 0.1 \ m/s, \mu = 0.3)。
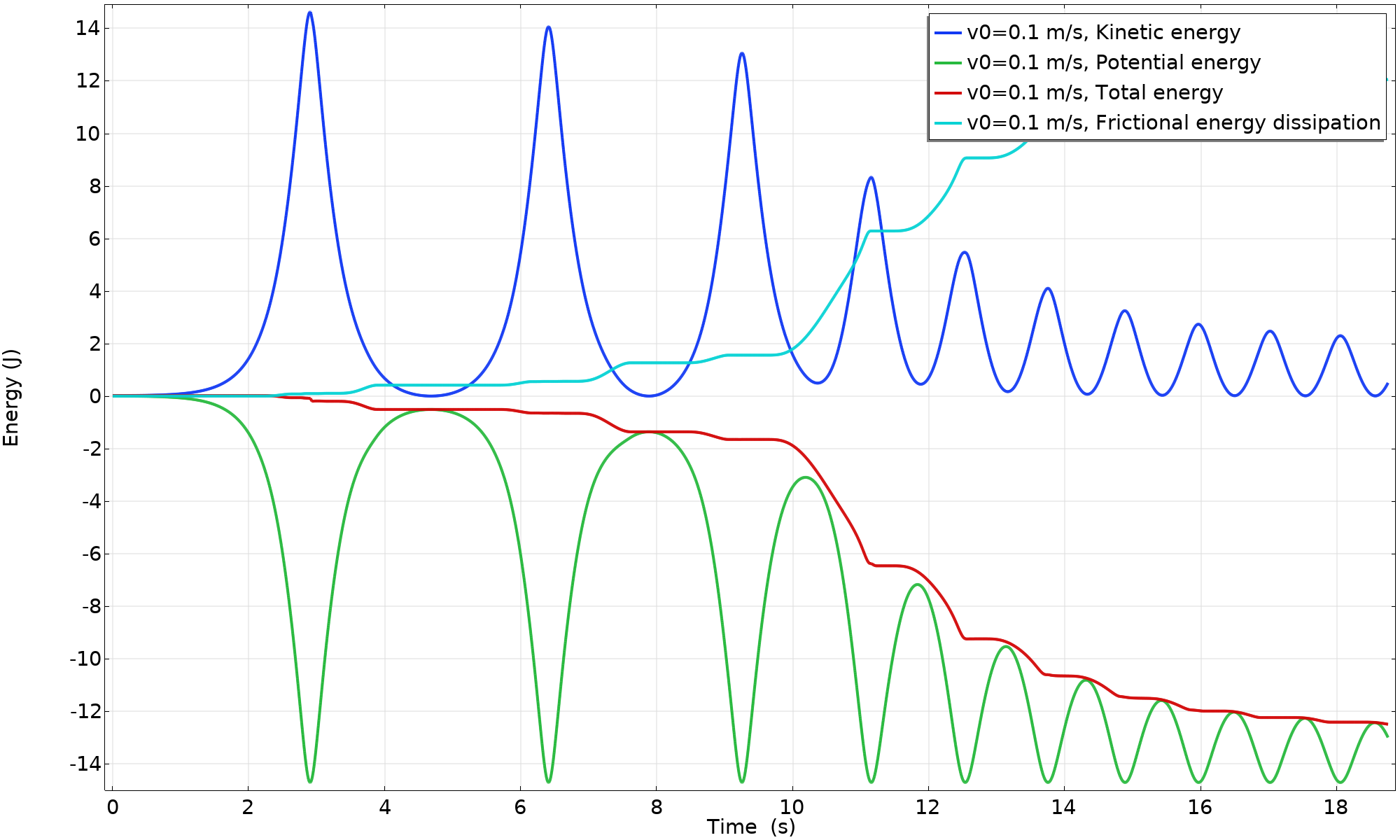
能量平衡(v_{0} = 0.1 \ m/s, \mu = 0.3)。
结束语
我们可以将上文中的 2D 动画扩展为 3D,请看下面的运动动画,其中 v_ \textsl {0} = 3.1 \ \text {m/s}。
在这篇博客中,仿真结果表明,跳环的行为比你刚开始想象的要复杂得多。点击下面的按钮下载教程模型,尝试自己分析跳环运动:
更多资源
想进一步了解这种跳环现象吗?请查看以下资源:






评论 (0)