
当导体材料附近存在时变磁场时,会发生电动磁悬浮现象。在本篇博客文章中,我们将通过两个示例来演示如何模拟这一现象。这两个示例分别为电动磁悬浮装置的 TEAM 标准问题和电动悬浮轮。
什么是电动磁悬浮?
永磁体或载流线圈在旋转和/或移动时会产生时变磁场,此时附近的导体便会发生电动磁悬浮现象。这是因为时变磁场会在导体中引起涡流,并使其产生相反的磁场,进而导致导体材料和磁源之间产生排斥力。这一过程是所有磁悬浮系统的基本工作原理。

一块磁铁悬浮在超导体上方。图像由 Julien Bobroff 自行拍摄。已获 CC BY-SA 3.0 许可,通过 Wikimedia Commons 共享。
分析电动磁悬浮的标准问题
我们首先来看看一个基于瞬态电磁分析方法(TEAM)问题 28:电磁悬浮装置的基准模型。该模型包含了一个铝制的导电圆盘,圆盘下方是两个圆柱形的同心线圈,两个线圈承载着方向相反的正弦电流。模型的横截面图和尺寸如下图所示。
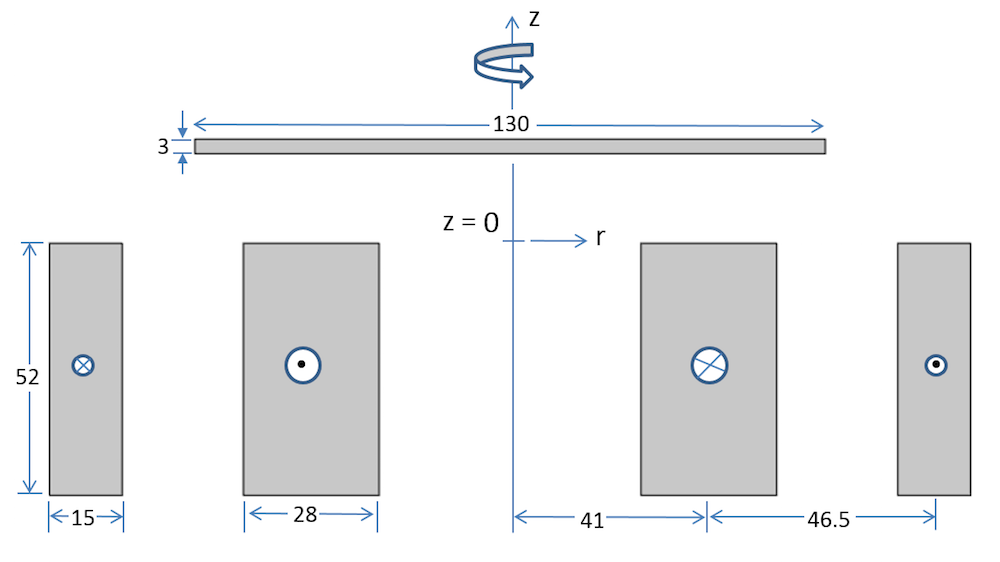
同心线圈和铝盘的横截面视图。所有尺寸均采用毫米为单位。
下图为电动磁悬浮装置的三维模型。
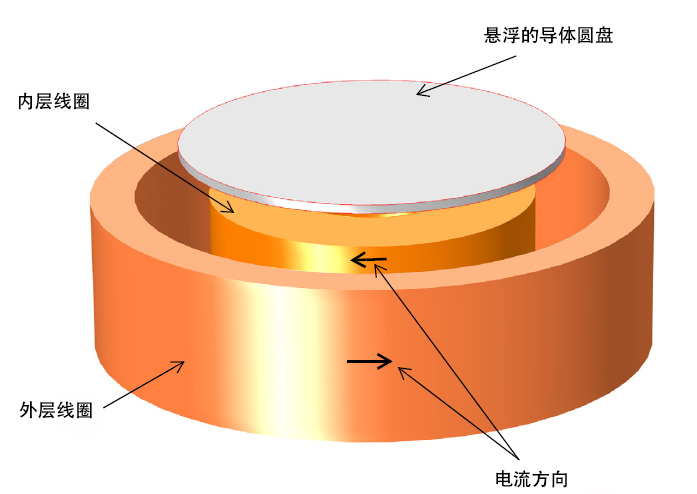
电动悬浮装置的三维模型,图像显示了悬浮的圆盘和两个同心线圈(承载的时变电流方向相反)。
我们在 COMSOL Multiphysics® 软件中使用了二维轴对称几何来对磁悬浮设备进行模拟。由于设备中存在时变电流和感应涡流,所以我们选择使用 AC/DC 模块中的磁场 接口来模拟磁场。此外,我们还使用了均匀多匝线圈 模型中的单个线圈 特征对承载反方向电流的线圈进行模拟,并通过计算力 特征计算出了铝板中的电动力,该特征计算出了麦克斯韦应力张量。
借助全局常微分和微分代数方程 接口,我们将铝板的刚体动力学以常微分方程(ordinary differential equation,简称 ODE)组进行求解。位置和速度的一阶常微分方程为:
由于电磁力会随着铝板和线圈之间距离的变化而不断改变,因此我们必须对磁场 接口进行求解,以获取铝板位置的动态变化数据。考虑到这一点,我们还使用了移动网格 接口来模拟铝板的移动。在完成对振荡圆盘位置的仿真研究后,我们将仿真结果与 TEAM 基准数据进行了比较,如下图所示。
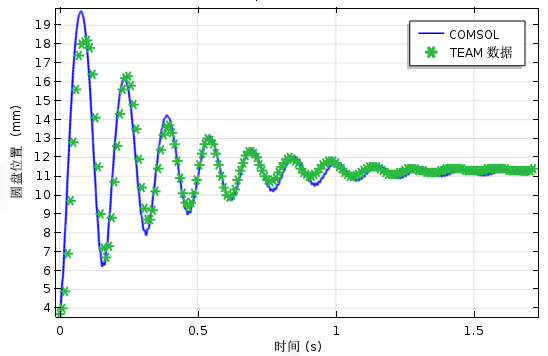
仿真结果与 TEAM 数据的对比。图像展示了铝板垂直振荡和时间的函数关系。
动画演示了 0.6 秒内导电圆盘在两个同心线圈上方的振荡情况。
在 COMSOL Multiphysics® 中模拟电动轮装置
磁源的机械旋转(例如径向磁化的 Halbach 转子)会在被动导电导轨(例如铝)上方引起感应涡电流。涡电流进而会产生与源磁场相反的磁场,在两个磁场的相互作用下,同时产生了升力与推力。此类装置被称为电动悬浮轮(electrodynamic wheel,简称 EDW)。
下图展示了 EDW 悬浮概念在高速运输领域中的应用。相对滑移速度 sl 决定了装置是产生推力还是制动力,它是圆周速度 vc 与平移速度 vx 之差,即 sl = vc — vx,其中 vc = ωmro 且 ωm = ωeP。ωm 在此处表示转子的机械角速度,ωe 表示电角速度,P 表示 Halbach 转子中的极对数量。
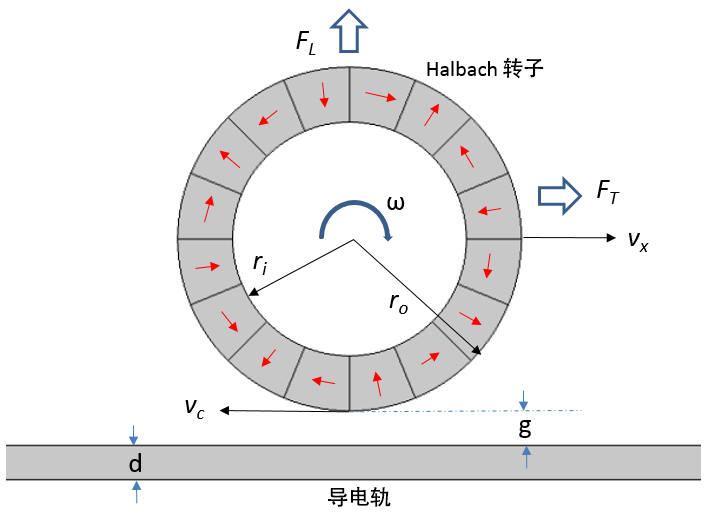
包含四个极对式 EDW 的磁悬浮火车的概念设计图,图像描绘了导电轨道以及旋转和/或行进中的 Halbach 转子。
如果圆周速度大于平移速度(相对滑移速度为正),则系统产生推力。若情况相反,则产生制动力。
通过使用二维和三维的旋转机械,磁 接口,我们可以在一个模型中同时模拟平移和旋转运动。具体操作包括:首先使用指定旋转速度 特征来定义旋转运动,然后使用符号相反的速度(洛伦兹) 项来描述导电轨道上磁悬浮系统(Halbach 转子)的平移运动,接着使用默认的安培定律 特征来模拟永磁体,同时将剩余磁通密度设为 Br = 1.42[T]。由于磁化方向为径向或沿方位角方向,方便起见,我们选择使用圆柱坐标系。
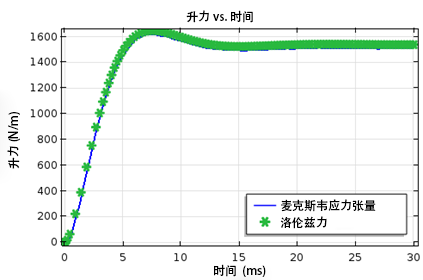
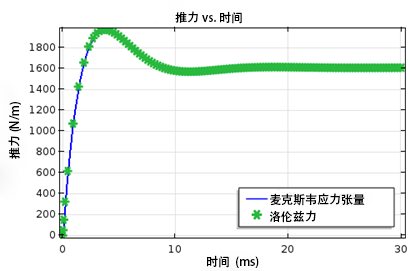
最后,我们通过执行瞬态仿真来求解转子机械角速度的阶跃变化。升力和推力随时间的变化情况如下所示,在这里,我们使用了两种不同的方法对这两种力进行计算,分别是麦克斯韦应力张量(使用“计算力”特征)和洛伦兹法。
升力(左图)和推力(右图)与时间的函数关系,两张图像中均显示了由麦克斯韦应力张量和洛伦兹法计算出的结果。
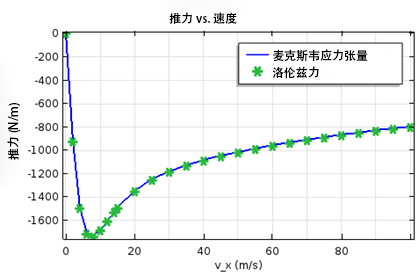
在第二步中,我们针对一定范围的平移速度执行了多次稳态仿真。当没有旋转运动,或者圆周速度小于平移速度时,则会产生曳力。下图显示了不同速度对应的升力和曳力的模拟结果。
磁浮系统中的升力(左图)和曳力(右图)与速度的函数关系,两张图像中均显示了由麦克斯韦应力张量和洛伦兹法计算出的结果。
动画演示了空气和磁铁中磁通密度的表面图,导轨中的电流密度和磁矢势 Az 的等值线图,同时还绘制了 Halbach 转子的顺时针旋转和场的相互作用。
电动磁悬浮装置模拟总结
在本篇博客文章中,我们演示了如何使用 COMSOL Multiphysics 和 AD/DC 模块来模拟两种类型的电动磁悬浮装置。同时我们还探讨了 TEAM 问题 28:电动悬浮装置,并将仿真结果与文献中的实验数据进行了比较。此外,我们还详细解释了电动轮磁悬浮系统的工作原理。并针对角速度的阶跃变化和不同的平移速度进行了多次仿真分析,最终计算出了由系统产生的升力和曳力/推力。
扩展阅读
- 深入了解本文涉及的示例:
- 了解其他用户如何使用 COMSOL Multiphysics 来求解类似的磁悬浮系统
- 浏览电磁设备系列中的其他博客文章
- 如果您想使用 COMSOL Multiphysics 来模拟磁悬浮系统,或者对于手中的建模过程有其他疑问,请随时联系我们







评论 (6)
晓飞 姚
2017-07-07赞!!!这个案例可以直接指导我来做一种电磁机构的仿真计算,非常感谢!
宇航 秦
2017-07-10姚飞晓,您好!
非常高兴能够帮助到您~
新江 严
2018-07-19请问案例上写的移动网格的参数化可以解释一下参数化思想吗?
Tengyue Gao
2018-08-14新江 严,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
ZH C
2022-04-24想问下,电动磁悬浮中s1,s2的几何映射怎么理解
Qihang Lin
2022-05-11 COMSOL 员工您好,这个案例使用了动网格进行模拟,动网格功能在使用时会令空间坐标系与材料坐标系分离。但模型中假设仪器基于刚性移动,为了简化建模并未使用固体力学接口以提供材料坐标系中的位移信息以及变化情况,因此需要手动设置s1与s2映射辅助动网格进行几何结构以及网格的移动。