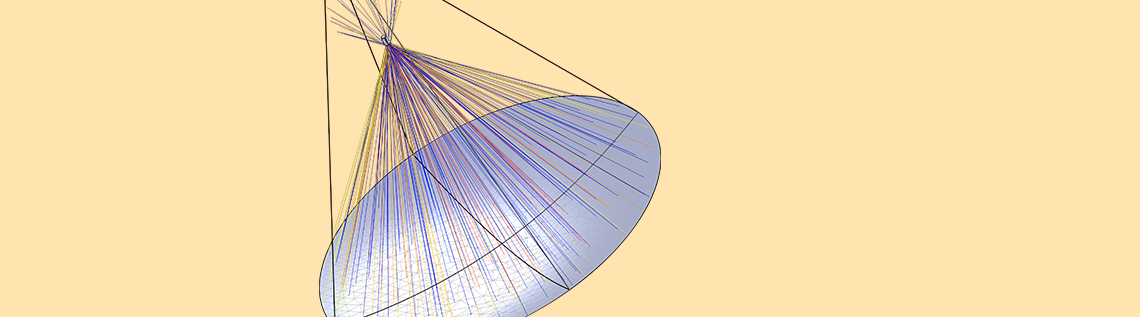
碟式抛物面太阳能收集器能使太阳辐射集中到一个很小的目标或腔式收集器上。由于太阳能在一大片区域内进行收集,因此收集器的入射热通量相当高。这种热能随后可以转换成电能,或用于制造化学能源,如氢气。今天,针对典型太阳能碟式聚光器/收集器系统焦平面上的热通量分布,我们将讨论几种计算方法。
太阳热能:一种高效的能源
太阳能聚光器/收集器系统的基本工作原理如下:入射的太阳辐射经曲面反射,集中到一小块区域,然后向蒸汽涡轮发动机这样的热机发动机供电。为尽可能将太阳辐射集中到最小区域,反射器的最佳形状是槽式抛物面或碟式抛物面(如下图所示)。

收集太阳能的碟式抛物面和一台维护吊机。图像由 Thennicke — Own work 提供。在 CC BY-SA 4.0 许可下使用,通过 Wikimedia Commons 共享。
热机的最大理论效率随着最高温度上升而提高,但在实际应用中,超过一定温度后,材料的选择就十分有限。因此,人们转而考虑尽可能精确地预测腔式收集器的工作温度。
在预测温度分布时,一个重要的指标是集中度(见参考文献 1 和参考文献 2),它表示腔式收集器表面的入射通量占周围太阳能通量的比例。辐射聚焦的区域越小,集中度就越高;或者系统中的辐射损失减少,比如碟式抛物面的表面吸收,则集中度也越高。在制造氢气这样的应用中,热通量的均匀性对整个制造过程的效率会产生很大影响。因此,我们必须考虑集中度如何随收集器的表面发生变化。
收集器有很多种形状,参考文献 1 研究了其中几种,但在本篇博客中,我们仅研究碟式太阳能收集器焦平面上的热通量。
预测理想太阳能收集器的集中度
在理想情况中,抛物面反射器能将射线集中于一点。但是,即使忽略了几何光学中的衍射,还是存在许多干扰因素导致无法实现这一理想情况。
让我们看一看系统中有哪些干扰因素会限制抛物面反射器的聚焦能力。
吸收
入射太阳能的一部分会被抛物面镜面吸收,而不是反射出去。甚至新的镜面也会吸收一些入射能量,更不要说长年的磨损更是会大大降低其性能。参考文献 3 中描述的情况就是一个典型示例。
表面粗糙度
实际的镜面不可能完全光滑。碟式抛物面的面法向方向总会和理想情况有一定偏差。这导致太阳辐射的聚焦不会那么完美,热通量会分散到焦平面的更大区域。
太阳形状
如果太阳是个极小的辐射源,那么所有入射太阳射线几近平行。然而,事实并非如此。即使在 1.5 亿千米距离之遥,太阳仍旧如此之大,以至从太阳圆面不同位置发出的射线之间存在明显的夹角,从而可以清晰地观察到太阳射线上的角度扩展。到达地球后,从太阳圆面发出的射线形成一个半角为 4.65 毫弧度的圆锥体。还有来自太阳周边区域的辐射,即环绕太阳的发光区域,但本例不考虑太阳周边的辐射。
广义上看,太阳形状,这一术语指的是太阳圆面的有限尺寸。太阳形状除了引起射线方向的分布外,还使太阳圆面不同位置的辐射具有不同的相对强度(参考文献 4)。 太阳圆面中心的辐射通常比其边缘发出的辐射强,这种现象称为太阳临边昏暗(参考文献 5) 。使用射线光学模块,不管是否涉及太阳临边昏暗效应,都会考虑太阳有限尺寸的影响。
同表面粗糙度一样,太阳形状会使入射热通量分散到焦平面的更大区域。以下绘图显示了理想情况下反射器焦平面的集中度(仅考虑有限太阳直径;查看参考文献 2)以及实际发射器的集中度(考虑到有限太阳直径、太阳临边昏暗、表面粗糙度和吸收,如参考文献 1 所述)。该碟式抛物面的临边角为 45 度,焦距为 3 米。
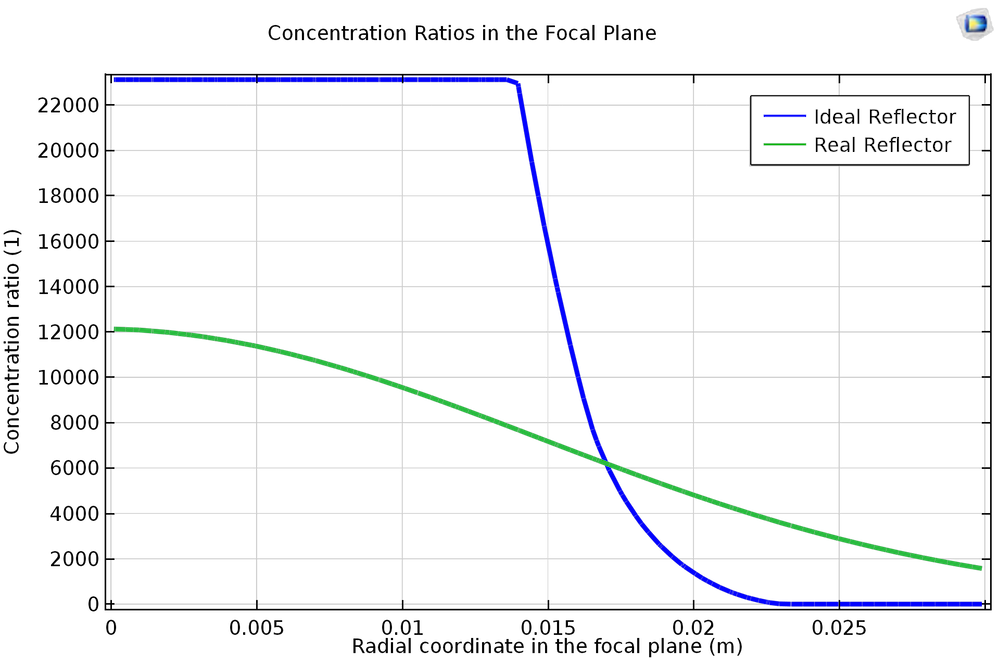
理想和实际反射器焦平面的集中度。
Monte Carlo 射线追踪解决方法
有几个不同的计算模型可用于预测碟式抛物面焦平面的集中度。Monte Carlo 射线追踪仿真已用于计算有限光源直径、太阳临边昏暗、表面粗糙度以及碟式抛物面的吸收(参考文献 1)。半解析模型还可用于计算更理想的结果,其中考虑了太阳的有限尺寸,但忽略了太阳临边昏暗、表面粗糙度和吸收(参考文献 2)。
使用射线光学模块,可以利用受照面功能释放从碟式抛物面表面直接反射的太阳辐射。射线到达收集器后,可以利用沉积射线功率功能来计算焦平面的热通量。
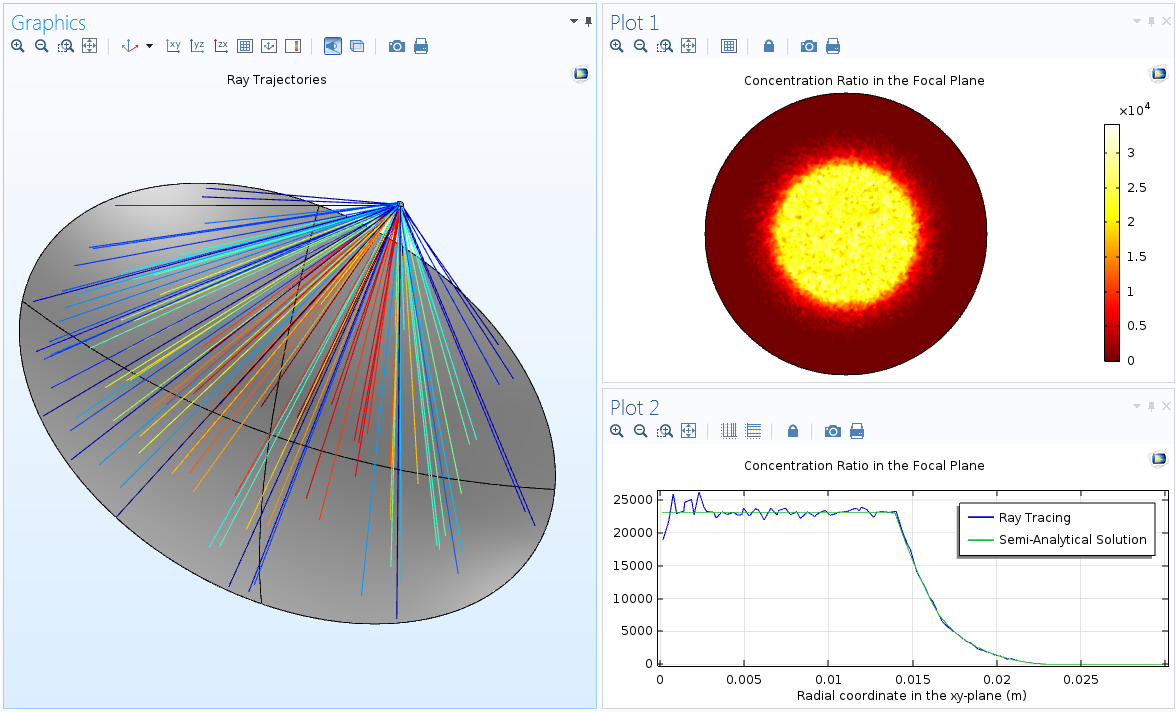
反射线的轨迹(左图)、焦平面的集中度(右上图)以及方位平均集中度的径向位置函数(右下图)。
报告集中度
与 Monte Carlo 仿真的情况一样,焦平面的集中度通常含有一定的数值噪音,这是由初始射线方向的随机性所引起的。一些内置平滑选项可用于提升结果绘图的质量。增加仿真中的射线数量是消除统计噪音的另一种方式。或者,亦可使用广义投影组件耦合,通过对所有方位角积分,将集中度的平均值转换为焦平面上的径向位置函数:

原始数据(不光滑)、平滑后的集中度以及方位平均集中度的比较。
在中心处无法获取方位平均集中度(此处的积分发生在无限近的距离),但在其他位置,焦平面的集中度相当精确,且看起来相同。
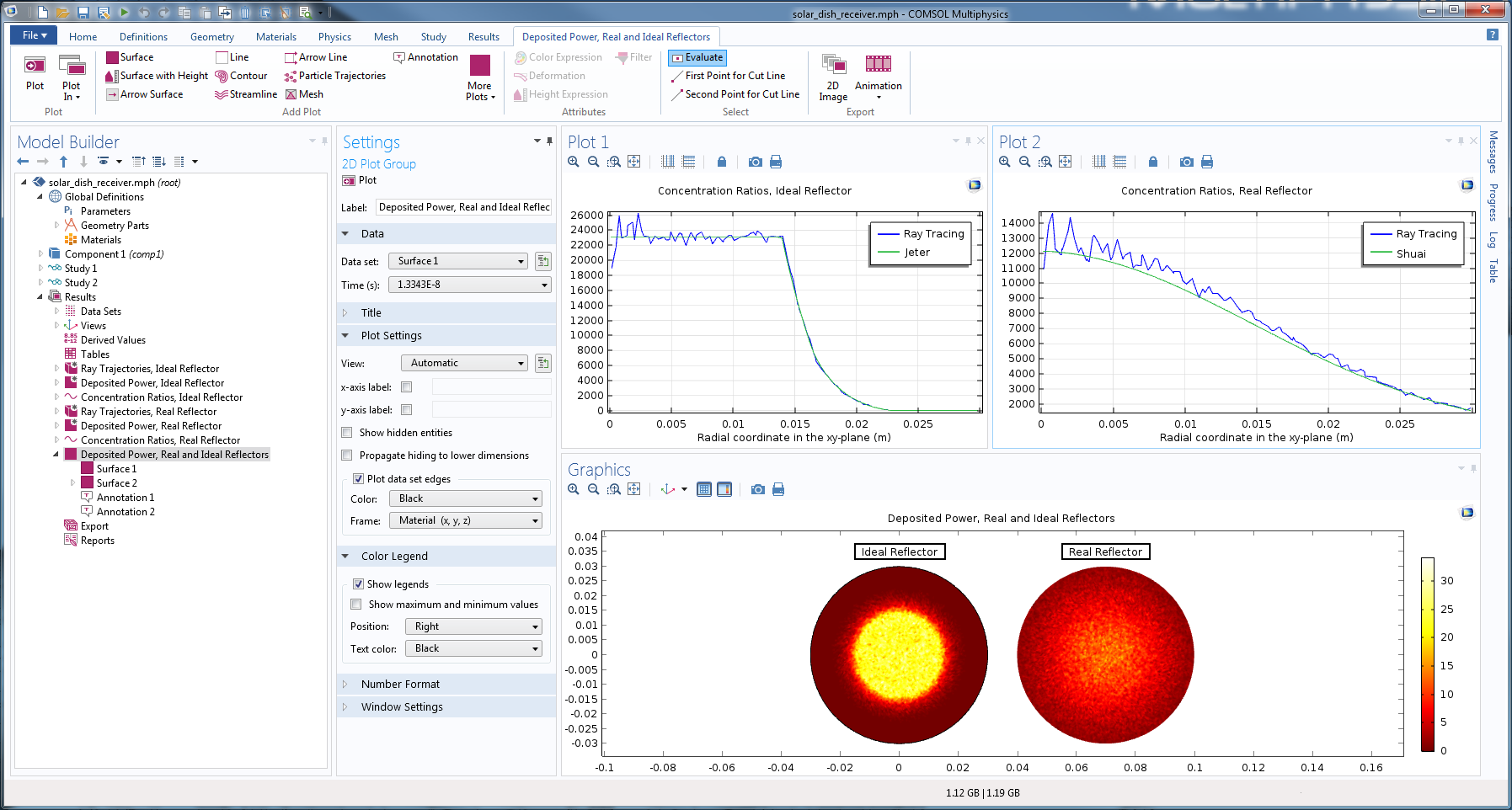
针对理想和实际反射器的解决方法在下图中并列显示。理想反射器的结果对比半解析法(参考文献 2),实际反射器的结果对比参考文献 1 中发表过的 Monte Carlo 射线追踪数据。结果与文献描述相当一致。统计噪音可以通过增加仿真中的射线数量进一步降低。
太阳能聚光器和射线光学的更多资源
- 了解更多关于太阳临边昏暗模型和参考文献 2 中半解析法的详细讨论,从“案例下载”中下载碟形太阳能收集器
- 阅读最新的 COMSOL Multiphysics 5.2a 中的射线光学模块新功能
- 在 “COMSOL 博客”中了解射线光学仿真的其他 App
参考文献
- Y. Shuai, X-L. Xia, and H-P. Tan, “Radiation performance of dish solar concentrator/cavity receiver systems,” Solar Energy, vol. 82, pp. 13–21, 2008.
- S. M. Jeter, “The distribution of concentrated solar radiation in paraboloidal collectors,” Journal of Solar Energy Engineering, vol. 108, pp. 219-225, 1986.
- G. Johnston, “Focal region measurements of the 20 m2 tiled dish at the Australian national university,” Solar Energy, Vol. 63, No. 2, pp. 117-124, 1998.
- M. Schubnell, “Sunshape and its influence on the flux distribution in imaging solar concentrators,” Journal of Solar Energy Engineering, vol. 114, pp. 260-266, 1992.
- D. Hestroffer and C. Magnan, “Wavelength dependency of the Solar limb darkening,” Astron. Astrophysl, vol. 333, pp. 338-342, 1998.






评论 (0)