旋转机械的振动对相互作用的各种旋转和静止部件的几何、结构和惯性特性非常敏感。这些特性包括安装部件的位置及其惯性特性、轴承特性和轴特性。要了解这些参数的影响,可以从一个简单的模型开始,然后进行各种分析以便在同一模型中关联转子响应。在这篇博文中,我们将用一个简支梁转子的例子来演示这个过程。
简支梁转子系统的两种分析类型
本例中的转子系统是一个简单的转子,在其整个长度上具有均匀的横截面。它的两端由轴承支撑,并且在转子的不同位置安装了三个被称为圆盘的组件。
我们可以使用 COMSOL Multiphysics® 软件中的 梁转子 接口对该转子进行建模。使用 圆盘 节点对转子组件的惯性特性和偏移量进行建模。通过 梁转子 接口中提供的 轴颈轴承 节点,使用基于等效刚度的方法对轴承支撑进行建模。
有关几何属性和模型设置的更多信息,请查看模型文档中的参考资料。
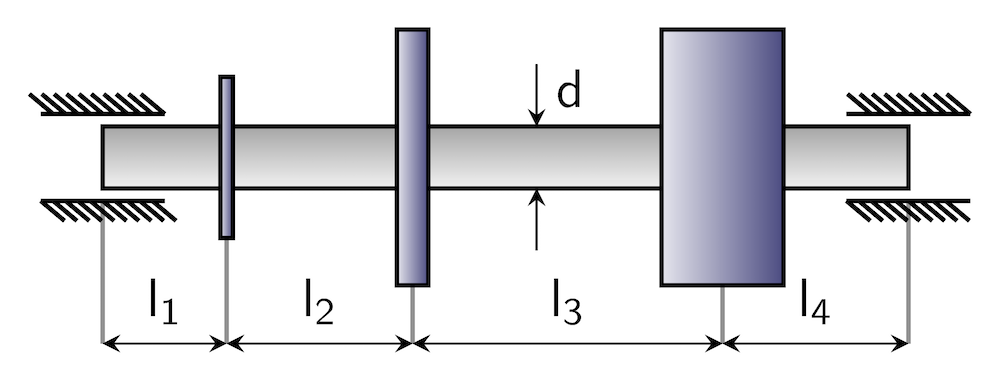
梁转子的几何示例。
研究转子振动特性通常采用两种分析方法:特征频率分析和时域分析。正如之前的一篇博客文章所述,转子的临界速度在很大程度上取决于转子的角速度。因此,在执行特征频率分析时,我们需要考虑转子速度的变化以获得正确的临界速度。当我们想要查看时变激励下的系统响应时,可以执行时域分析。
现在,让我们看看每个分析提供了什么类型的信息,以及执行这些分析所涉及的步骤。
转子的特征频率分析
特征频率分析用于确定系统的固有频率。在转子动力学场景中,这种分析可以以两种不同的方式使用。
首先,对于不固定系统的运行速度,可以对运行速度范围内的系统进行特征频率分析,选择离系统临界速度最远且满足其他设计考虑的速度。如果无法为当前系统找到合适的运行速度,可能需要在系统中进行某些设计修改以获得满足所有要求的稳定运行速度。
在第二种分析中,系统的运行速度是固定的。在这种情况下,需要在给定的运行速度下执行特征频率分析,以检查系统的任何固有频率是否不接近运行速度。如果任何一个固有频率接近运行速度,那么必须进行设计修改。
转子系统中的设计修改需要了解什么样的修改会产生预期的效果和成本。这就是通过模拟简单系统来了解设计修改的效果非常有帮助的地方。仿真可以为设计修改提供指导,从而减少设计过程中的迭代次数。
考虑第一种情况,系统的运行速度不固定,以了解分析步骤。在这种情况下,需要对转子的角速度执行参数化特征频率分析。这需要在研究 节点中执行两个步骤:参数化扫描和步骤1:特征频率,如下图左侧所示。下图中间显示了对代表转子角速度的参数Ow 进行扫描的参数化扫描节点的设置。此参数用作梁转子 节点的转子转速 部分的设置输入,如下图右侧所示。
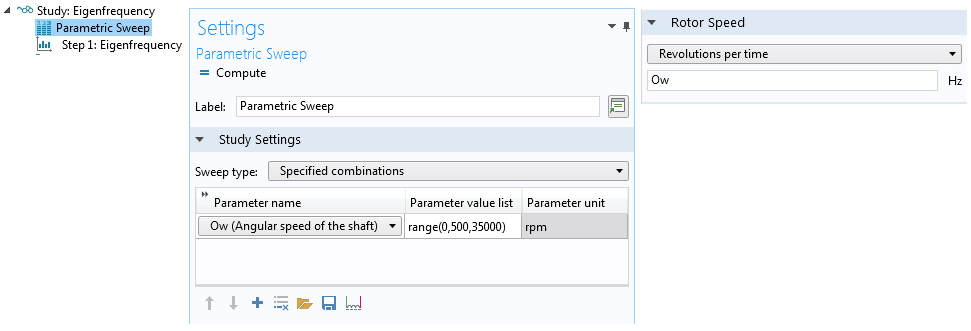
步骤研究节点(左)、参数扫描设置(中间)和转子速度输入(右)。
执行分析后,我们会得到一个如下所示的回旋图。回旋图显示了给定转速和固有频率组合下转子的回旋轨迹和变形形状。

转子回旋图。
转子的变形形状还可以让我们了解到转子角速度对固有频率的影响有多大。如果圆盘在没有明显倾斜的情况下远离旋转轴,则向后旋转(与自旋相反)和向前旋转(与自旋方向相同)中的频率分裂就不明显。或者,如果圆盘没有明显远离旋转轴而是有明显的倾斜,那么向后和向前旋转的频率分裂是明显的。
为了深入理解这个概念,我们可以绘制不同模态的固有频率相对于转子角速度的变化曲线,这通常被称为 坎贝尔 图。简支转子的坎贝尔图如下所示。我们可以看到,对于某些模态特征频率与转子速度的强烈发散;而对于其他模态,特别是低固有频率的模态,发散并不明显。如果查看与这些频率对应的模态振型,它们会证实之前讨论的行为。通过查看固有频率与角速度曲线的交点ω=Ω,可以从坎贝尔图中获得转子的临界速度曲线。除非阻尼足够,否则转子不应在这些速度附近运行。
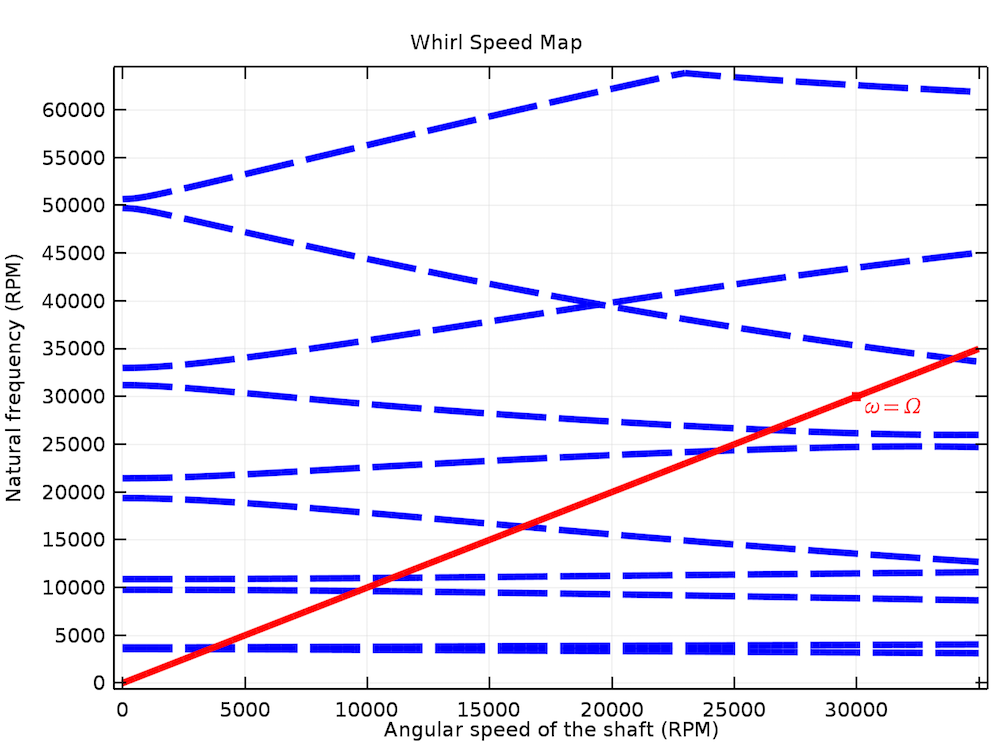
简支转子系统的坎贝尔图。
通过绘制转子角速度的对数衰减图,可以获得相应模式下的阻尼。对数递减可以定义为
其中,A(t)是时变响应,ω 是系统的复特征频率。T 是由下式 T = \frac{2\pi}{Re(\omega)}
给出的时间周期。
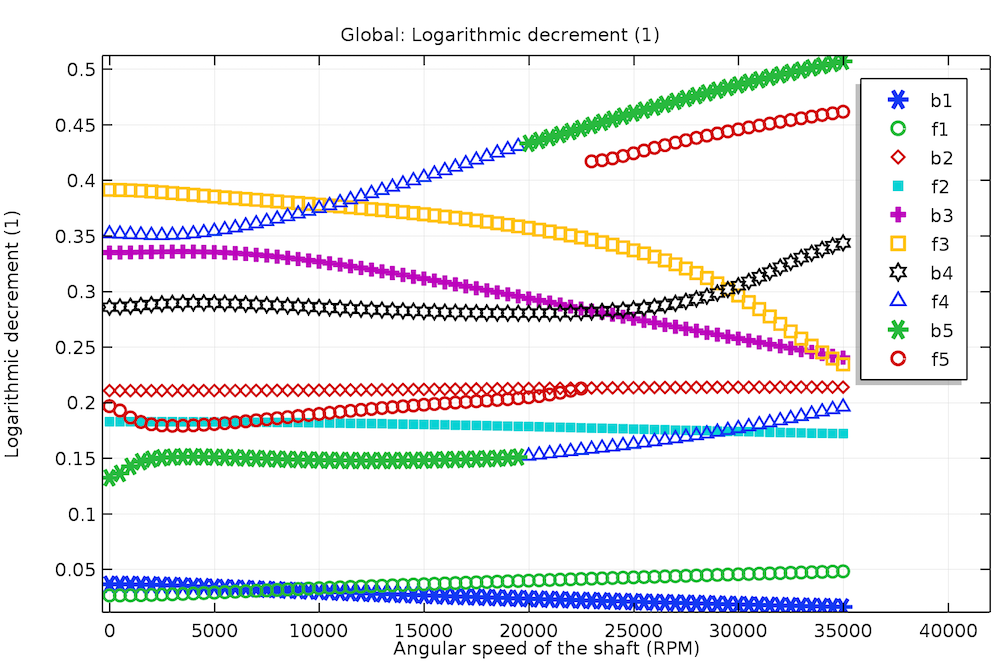
简支转子系统中不同弯曲模式的对数递减。
在上图中,我们可以看到不同弯曲模式的对数递减随简支转子角速度的变化。符号“b”和“f”分别用于向后和向前旋转模式。对数递减为零表示系统无阻尼,负值表示系统不稳定,正值表示系统稳定。
我们还可以注意到一些曲线的图案变化。原因是模态数据按固有频率的递增顺序排列。但是我们知道,转子的固有频率在向后旋转模式下降低,在向前旋转模式下增加。因此,在超过一定角速度的情况下,较高的后向旋转模式和较低的前向旋转模式之间存在固有频率的交叉。这扰乱了模式的初始顺序,导致模式在交叉点之间切换。
转子的瞬态分析
特征频率分析给出了在稳态下运行的转子系统的特性。然而,在达到稳态状态前后,在加速和减速过程中,转子的角速度随时间而变化。在某些情况下,运行速度可能高于转子的前几个固有频率。因此,在加速和减速过程中,转子将跨越相应的临界转速。此外,可能存在作用于转子的非谐波时变外部激励。在这种情况下,转子响应不能完全由特征频率或频域分析确定。相反,我们需要瞬态模拟来研究系统的响应。
我们还可以通过执行参数化扫描来对不同角速度下的转子进行瞬态分析,以查看角速度如何控制响应。这种分析的一个明显扩展是评估所有角速度下转子随时间变化的响应频谱,并分析角速度和频率的哪些组合会导致高振幅响应。瀑布图 显示了响应幅度与角速度和频率的关系,并给出了不同速度下参与响应的模态分布。这样的分析可以使用研究节点中的三个步骤来设置,如下所示。

瀑布图分析的步骤。参数化扫描研究步骤用于扫描角速度,瞬态研究步骤用于执行与参数扫描中的每个角速度相对应的瞬态分析,以及时域到频域 FFT 研究步骤将时间相关数据进行快速傅立叶变换,转换成频谱。
在特征频率分析中,使用恒定刚度和阻尼系数对轴承进行建模。然而,实际上,这些系数强烈依赖于轴颈运动。为了突出非线性对时域分析的影响,使用滑动轴承模型代替恒定轴承系数。对于短轴承近似,滑动轴承模型是基于雷诺方程的解析解。在这种情况下,系统是自激的,因为偏心安装模拟为圆盘。为了简化系统,只考虑在局部 y 方向上偏心率较小的第二个圆盘。
位移 z 分量的瀑布图如下图所示。您可以在频谱中清楚地观察到三个峰。第三个峰值,沿着 ω=Ω 曲线,对应于 1X 同步旋转。这是对离心力的响应,因为离心率会随着轴的旋转而改变其方向。由于复杂的转子轴承相互作用,其他峰值对应于转子的轨道运行。原因是来自轴承中轴颈周围压力分布产生的力与轴颈运动存在交叉耦合效应。换句话说,轴颈在一个横向方向上的运动引起了在与其垂直的横向方向上的分力。这种现象的效果是在转子向前旋转的方向上作用一个净力。这导致转子的次同步轨道运行。
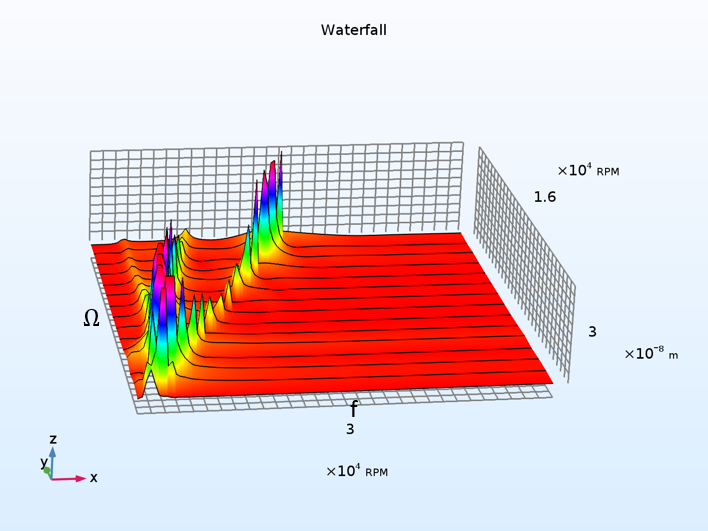
瀑布图显示了响应幅度与转子角速度和频率的关系。
在 30,000 转/分时,沿转子长度的不同位置的轨道如下所示。随着时间的推移,轨道曲线的颜色从绿色变为红色。可以看到,在初始瞬态阶段之后,转子在稳态下经历了向前的圆周旋转。此外,第二弯曲模式在响应中的参与度最高。
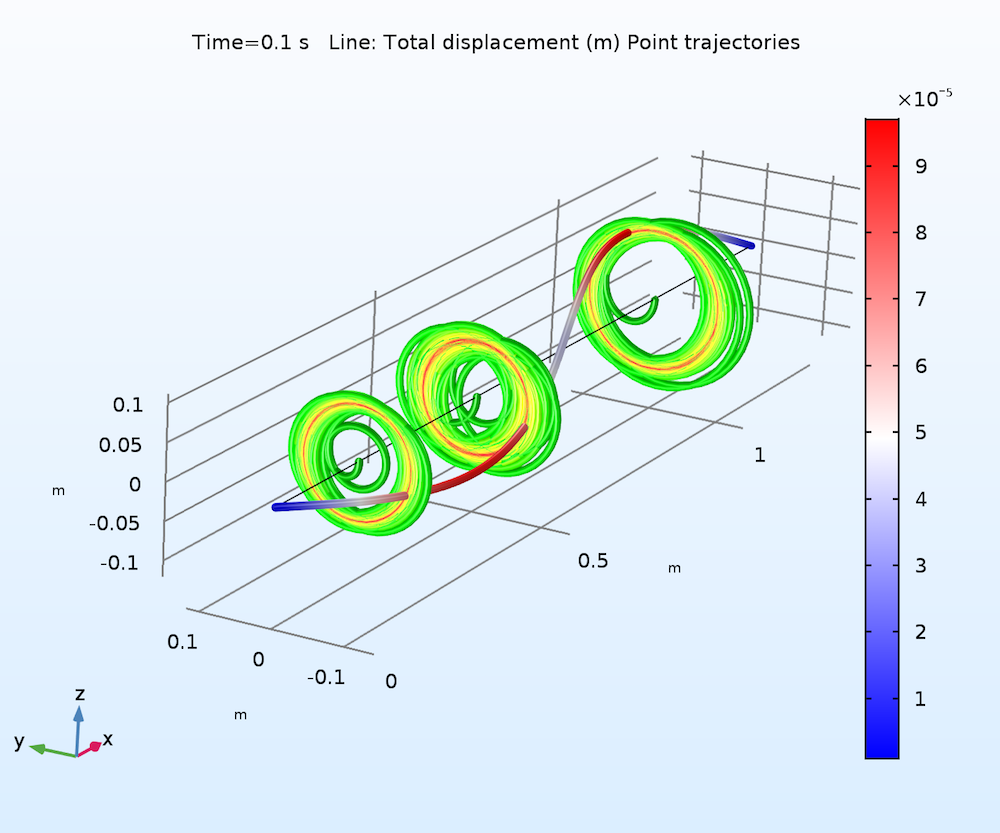
转子在不同位置的轨道。该图随时间由绿色变为红色。
转子上的某一点在 30,000 转/分时 z-方向位移的时间变化如下所示。除了高频变化之外,还有一个低频分量包络着响应,但会随着时间的推移而衰减。
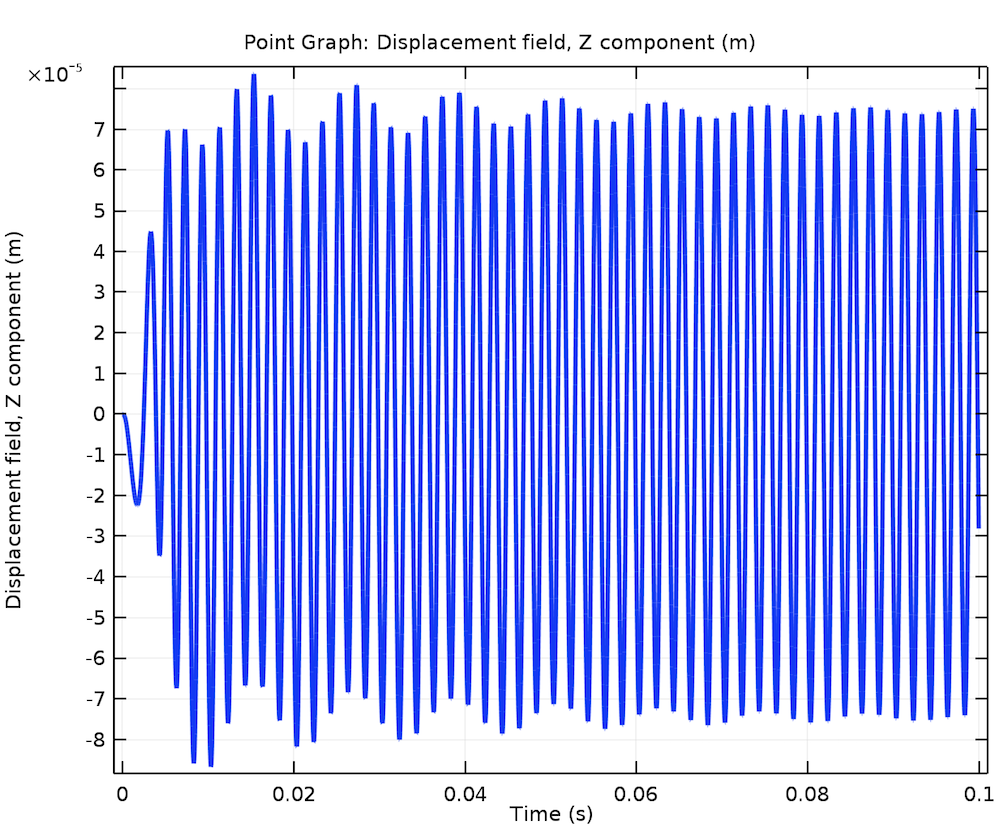
z-位移的时间变化。
通过本教程模型,我们演示了在转子系统中建立不同分析的方法,以及如何绘制和分析仿真结果。准备好自己动手尝试这个教程了吗?只需点击下面的按钮,即可通过 COMSOL 网页的“案例下载”页面访问MPH文件,或者通过COMSOL软件中的案例库打开它。
了解更多关于分析转子动力学应用的信息
- 了解转子动力学模块的特性
- 查看如何模拟往复式发动机以优化其设计






评论 (0)