
当我们为高速、高数据速率通信研究相控阵天线并创建原型时,通过使用天线阵列系数可以节省时间和计算成本。这样,我们就无需通过一个完整的三维波动方程来分析整个结构。
天线在物联网,IoS,SatCom 和 5G 中的应用
在当今生活中,有一些常见的射频流行语,比如物联网(IoT),空间互联网(IoS),卫星通信(SatCom)和5G。通过更高的数据速率和工作频率,使得人们满足对无线通信的需求,同时也使带宽比以前高得多也宽得多。
当我们通过5G移动网络发送或接收信息信号时,其预期的工作频率比传统移动系统的工作频率高得多,因此不可避免地会存在电磁波的明显衰减,导致信号完整性问题。为了使通信系统可以在有限的功率下使电磁波传播更长的距离,我们有必要部署一个高增益天线,该天线可以塑造像很尖锐的铅笔状波束一样的远场辐射方向图。这使我们能够在更长距离内不间断地传递信息。

大碟形天线使我们可以进行长距离通信。通过 Wikimedia Commons 在公共领域中的图像。
孔径天线,如蝶形天线和喇叭天线,将为上述目的提供足够高的增益。这些高增益天线的远场辐射方向图具有非常窄的角度扫描范围,并且电磁波的可见区域是有限的。为了扩大通信覆盖范围,可以通过使用一个万向架在机械上旋转天线来扩展其扫描能力。然而,孔径天线需要大量空间才能安装,并且可能不适合在消费类电子产品中使用(您不会想在手机上安装一个大型碟形天线!)
甲单极天线阵列示出光束扫描能力。
简而言之,天线阵列就是一组由特定空间和相位结构连接起来的天线。阵列可以克服上述障碍,并且可以根据天线单元的类型进行保形和小型化,从而形成阵列和材料特性。
如果小型化是一个设计元素,那么选择合适的天线单元非常重要。设计规范可以决定需要部署哪种类型的天线单元。
使用阵列因子的好处
尽管天线阵列的体积小于孔径型天线的体积,但与单个天线相比,其仿真计算成本仍然很高。不需要对整个结构进行完整的三维模型仿真,也不需要牺牲过多的分析精度,我们仍然可以将阵列因子相乘,从单个天线元件的辐射方向图估计天线阵列的远场辐射方向图。
定义三维模型中的均匀阵列因子表达式为
\frac{sin(\frac
{n_x (2 \pi d_x sin\theta cos\phi + \alpha_x)} {2})}{sin(\frac{2 \pi d_x sin\theta cos\phi + \alpha_x}{2}
)} \frac{sin(\frac
{n_y (2 \pi d_y sin\theta sin\phi + \alpha_y)} {2})}{sin(\frac{2 \pi d_y sin\theta sin\phi + \alpha_y}{2}
)} \frac{sin(\frac
{n_z (2 \pi d_z cos\theta + \alpha_z)} {2})}{sin(\frac{2 \pi d_z cos\theta + \alpha_z}{2}
)}
其中 nx,ny 和 nz 分别是沿 x轴,y 轴和 z 轴的阵列单元数。dx,dy 和 dz 项是在仿真中使用以波长表示的阵列单元之间的距离。alphax,alphay 和 alphaz 项是弧度单位的相传播。
在上述阵列因子表达式中,输入功率未归一化。如果天线阵列被馈电网络分配的单个输入功率激励,则需要相应地缩放。
使用 COMSOL Multiphysics® 软件的优点之一是可以为后处理表达式键入任何类型的方程。当表达式比较复杂时,可以使用仿真 App 或模型方法来解决。
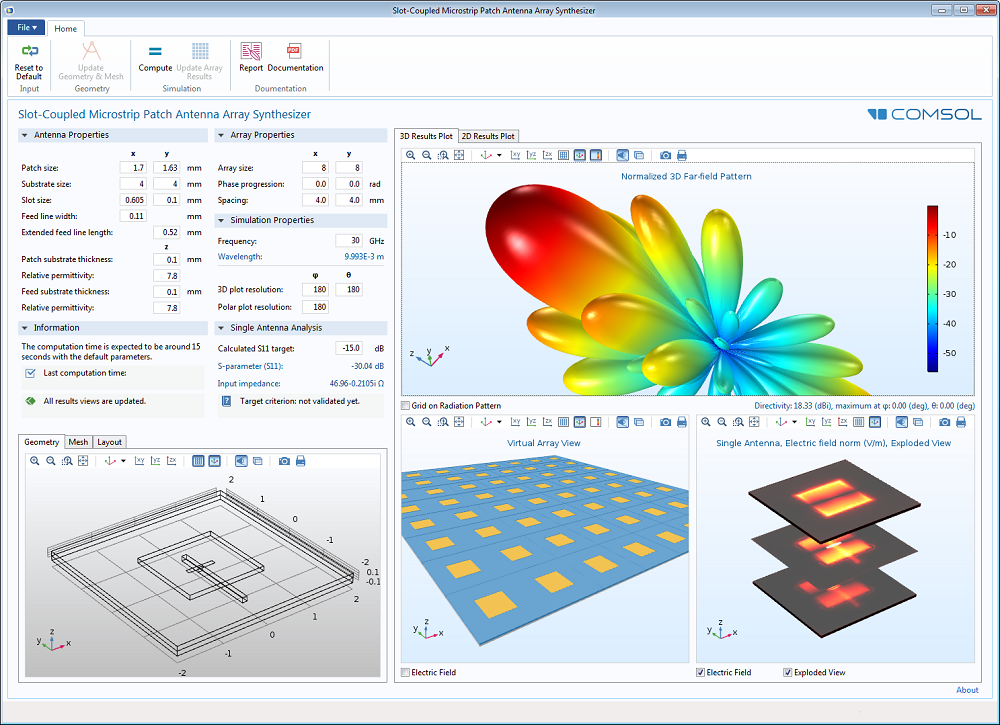
具有8×8虚拟阵列,电场分布和3D远场辐射方向图视图的天线阵列仿真案例库的用户界面。
将阵列因子方程与天线远场增益变量 emw.gaindBEfar 相乘,就可以计算出天线阵列的远场增益。
射频模块中的阵列因子功能
输入一个方程的表达式或使用方法功能编写简单的代码都可能成为快速学习的障碍。幸运的是,作为 COMSOL Multiphysics 的附加模块,RF模块提供了阵列因子后处理函数。在对具有远场域/计算物理场特征的单个天线进行仿真后,可从后处理上下文菜单的“ 定义” >“ 功能”下访问三维均匀阵列因子函数,其用于绘图表达式后为
af3(nx, ny, nz, dx, dy, dz, alphax, alphay, alphaz)
输入自变量的定义与上述均匀阵列因子方程相同,下表解释了其对结果图的影响。
| 影响 | 输入参数 |
|---|---|
| 阵列单元数 | 天线增益 |
| 阵列单元之间的距离 | 天线增益 旁瓣电平 |
| 相传播 | 主瓣转向方向 |
输入参数对辐射方向图的影响。
以 z 轴为主波束的虚拟 8×8 天线阵列的评估表示为
emw.gaindBEfar + 20 * log10(emw.af3(8,8,1,0.48,0.48,0,0,0,0))+ 10 * log10(1/64)
它以 dB 为单位进行计算,并且阵列因子与单个天线增益之间的乘法是通过表达式中的求和完成的。
| 输入参数 | 描述 | 值 | 单元 |
|---|---|---|---|
nx |
沿 x 轴 的单元数 | 8.00 | 无量纲 |
ny |
沿 y 轴 的单元数 | 8.00 | 无量纲 |
nz |
沿 z 轴 的单元数 | 1.00 | 无量纲 |
dz |
沿 x 轴的 阵列单元之间的距离 | 0.48 | 波长 |
dy |
沿 y 轴的 阵列单元之间的距离 | 0.48 | 波长 |
dz |
沿 z 轴的 阵列单元之间的距离 | 0 | 波长 |
alphax |
沿 x 轴的 相传播 | 0 | 弧度 |
alphay |
沿 y 轴的 相传播 | 0 | 弧度 |
alphaz |
沿 z 轴的 相传播 | 0 | 弧度 |
主波束沿 z 轴的虚拟 8×8 阵列天线的阵列因子输入自变量。
上述表达式假设天线阵列由单输入功率源均匀分布网络馈电。需要将其按10 * log10(1 /总单元数)的倍数缩放。
当使用非零相传播值时,可以将主波束的方向(即最大辐射)指向所需方向。阵列单元之间的距离是0.48个波长。当距离在0.45至0.5个波长之间时,预计其旁瓣电平约为 -12 至 -15 dB。
下面的方程有助于将相传播值定义为与主轴夹角的函数,这样可以方便地指定扫描方向。
\alpha_x=-kdcos\theta=\frac{2\pi d}
{\lambda}
cos\theta
其中 k 是波数,d 是天线单元之间的距离,theta 是与轴的夹角。
为了生成最大方向与x轴成60度角的波束,将 alphax(在阵列因子函数中)设置为
-2 * pi * 0.48 * cos(pi / 3)
“ 案例库”中的 “微带贴片天线” 教程 展示了如何使用阵列因子来演化单个天线的辐射模式。
以下极坐标图比较了三种辐射模式:
- 单个微带贴片天线的增益
- 模式设置为主瓣方向与 x 轴成 60 度和与 z 轴成30度的均匀阵列因子均匀的阵列因子
- 8×8 微带贴片天线阵列的合成增益
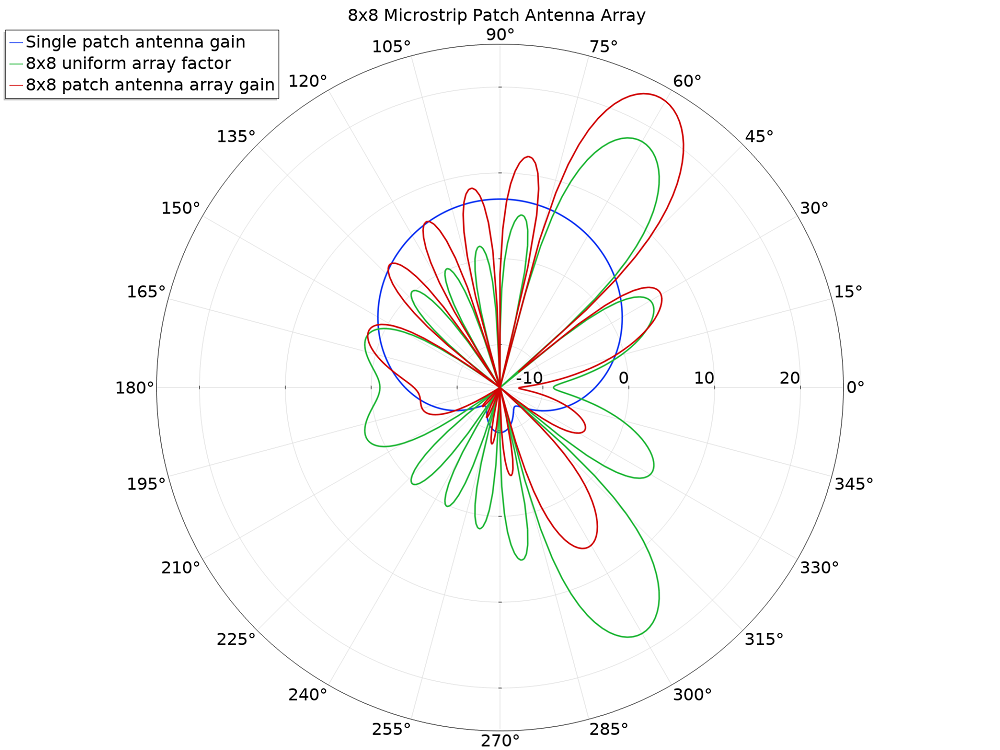
以dB标度绘制的单个贴片天线增益,8×8均匀阵列因子和8×8微带贴片天线阵列增益。

虚拟的8×8微带贴片天线阵列的远场增益模式。绘图的最小范围可能会改变主光束图案的视觉清晰度。
天线阵列仿真的后处理
COMSOL Multiphysics中的各种后处理选项使您能够有效地研究天线原型。在动画设置中为动画序列类型使用 全谐波动态数据扩展 是一种非常有用的方法,可以在不仿真每个角度扫描点的情况下,检查波束转向的可行性,而无需在每个角度扫描点都运行模拟。
 l
l
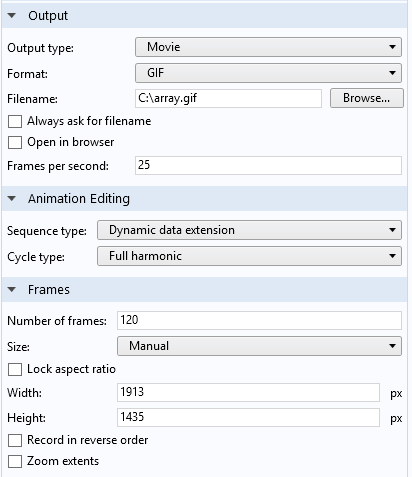
动画设置窗口。动态数据扩展用于扫描内部相位变量。
对于时谐频域仿真,可以在任意角度(相位)下求得因变量的解。全谐波动态数据扩展改变了内部定义的“ root.phase ” 变量从 0 更改为 2 pi,同时产生动画。
以下表达式生成 8×8 微带贴片天线阵列的动画,通过负 x 轴扫描 z 轴直到正 x 轴,总共 180 度范围内。
emw.gaindBEfar + 20*log10(emw.af3(8, 8, 1, 0.48, 0.48, 0, -2*pi*0.48*cos(phase+pi/2), 0, 0)) + 10*log10(1/64)
8×8 微带贴片天线阵列的远场增益模式。主波束沿一个轴移动。
扫描轨迹不必遵循直线或矩形栅格。可以使用以下表达式产生围绕 12×12 微带贴片天线阵列的,以 z 轴旋转的主波束方向图:
emw.gaindBEfar + 20*log10(emw.af3(12, 12, 1, 0.48, 0.48, 0, -2*pi*0.48*cos(pi/2-pi/8*cos(phase)), -2*pi*0.48*cos(pi/2-pi/8*sin(phase), 0)) + 10*log10(1/144)
12×12 微带贴片天线阵列的远场增益模式。主波束沿圆形轨道移动。
主波束与轴成 pi / 8 弧度的倾斜,在动画中绕轴旋转。
结束语
大型天线阵列系统的三维全波仿真需要占用大量内存,从而增加了计算时间和成本。通过使用前面讨论的渐近方法,将单个天线单元的远场后处理变量与均匀阵列因子相乘,可以快速估算天线阵列的辐射模式。然而,这种方法不能解决阵列单元之间的场耦合问题。因此,它仅适用于快速原型可行性研究。为了精确地检测增益和旁瓣电平,可能需要对整个阵列结构进行全波分析。
其他资源
查看以下模型案例可以通过仿真研究天线阵列:






评论 (0)