参数估计很少有醒目的插图,但往往对获得准确的材料数据,从而获得准确的模拟结果起着重要作用。它涉及最小化测量的实验结果与模型中的相应数据之间的差异。有时你可能需要结合几个实验的数据,就需要设置适当的权重,使所有的实验都能为估计的材料参数贡献信息。最大似然参数估计提供了一种根据客观标准自动选择权重的方法,以便从实验中提取最大数量的信息。
使用最小二乘法避免手动调整
最小二乘法是最大似然参数估计的一种特殊情况,它是基本参数估计的一个很好的起点,因此是一种很受欢迎的方法。COMSOL Multiphysics® 软件内置支持最小二乘法。
在这篇文章中,我们将演示如何利用最大似然参数估计来帮助避免为给定问题手动调整权重。

在这个示例中,两个参数的相对误差取决于为两组测量选择的权重。因此,准确地确定这两个参数需要在两个权重之间找到一个很好的折衷方案。
数据采样时的概率和统计
对于一个概率密度函数 f ,在一定范围内 [a, b] 对一个数据点进行采样的概率 P,以积分的形式给出
在这种情况下,我们只考虑测量点 x 周围的无穷小的范围 dx,所以概率变为
从这个意义上说,概率密度函数与由 dx 给出的概率之间存在直接关系。(为方便起见,dx 可以省略。)
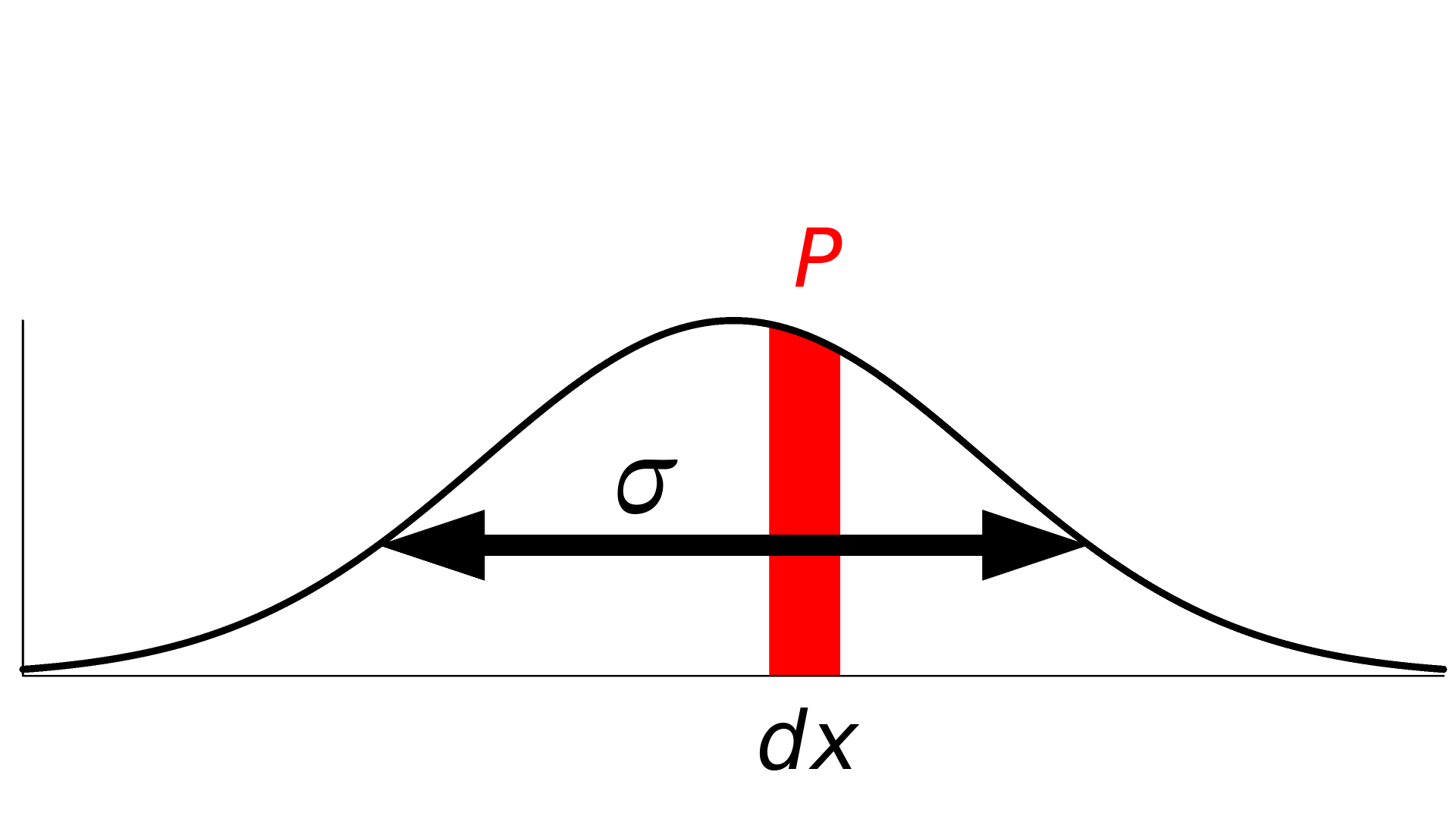
可以通过对概率密度函数进行积分来计算对某个值进行采样的概率。
最小二乘目标和最大似然参数估计
可以考虑模拟和实验之间的不同差异来源。在下面的例子中,我们将考虑来自实际测量的正态分布的不确定性,因此测量值 x^e 的概率变为
其中,\sigma 是测量误差的标准偏差,x 是平均值。对于n 次测量,我们可以将联合似然计算为乘积
我们可以取似然的对数来避免乘积和任何相关的数值计算困难。作为替代我们得到一个总和,类似于最小二乘目标:
在某种意义上,我们可以说 \sigma 在最小二乘目标中起到了权重的作用。因此,为了使可能性最大化,我们需要使方程的右边最小化,并且不用考虑\sigma 的取值,当平方差的和取最小值时,方程右边就会出现最小值。如果不同的测量结果集合中的 \sigma 值也不同,就不能得出同样的结论。接下来,我们来看这样一个例子。
拉伸试验的最大可能性
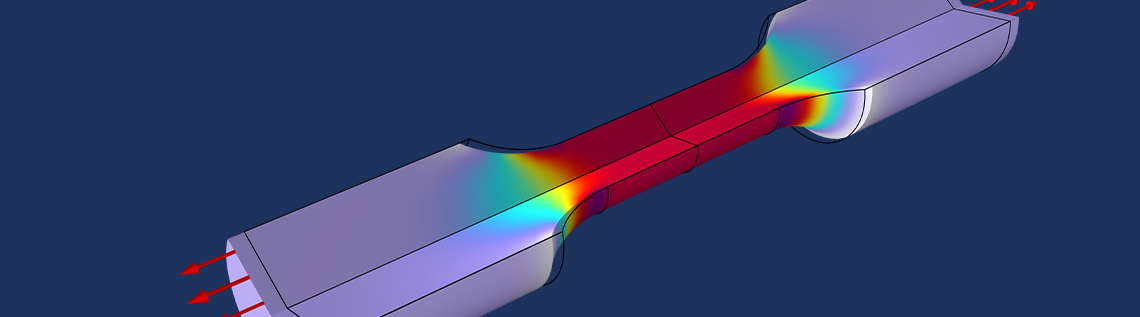
通常通过压缩试验来估计材料的泊松比,但为了便于演示,我们以一个使用拉伸试验来估计泊松比和杨氏模量的示例来说明。我们通过测量下图所示试样的拉伸力和径向收缩来实现。
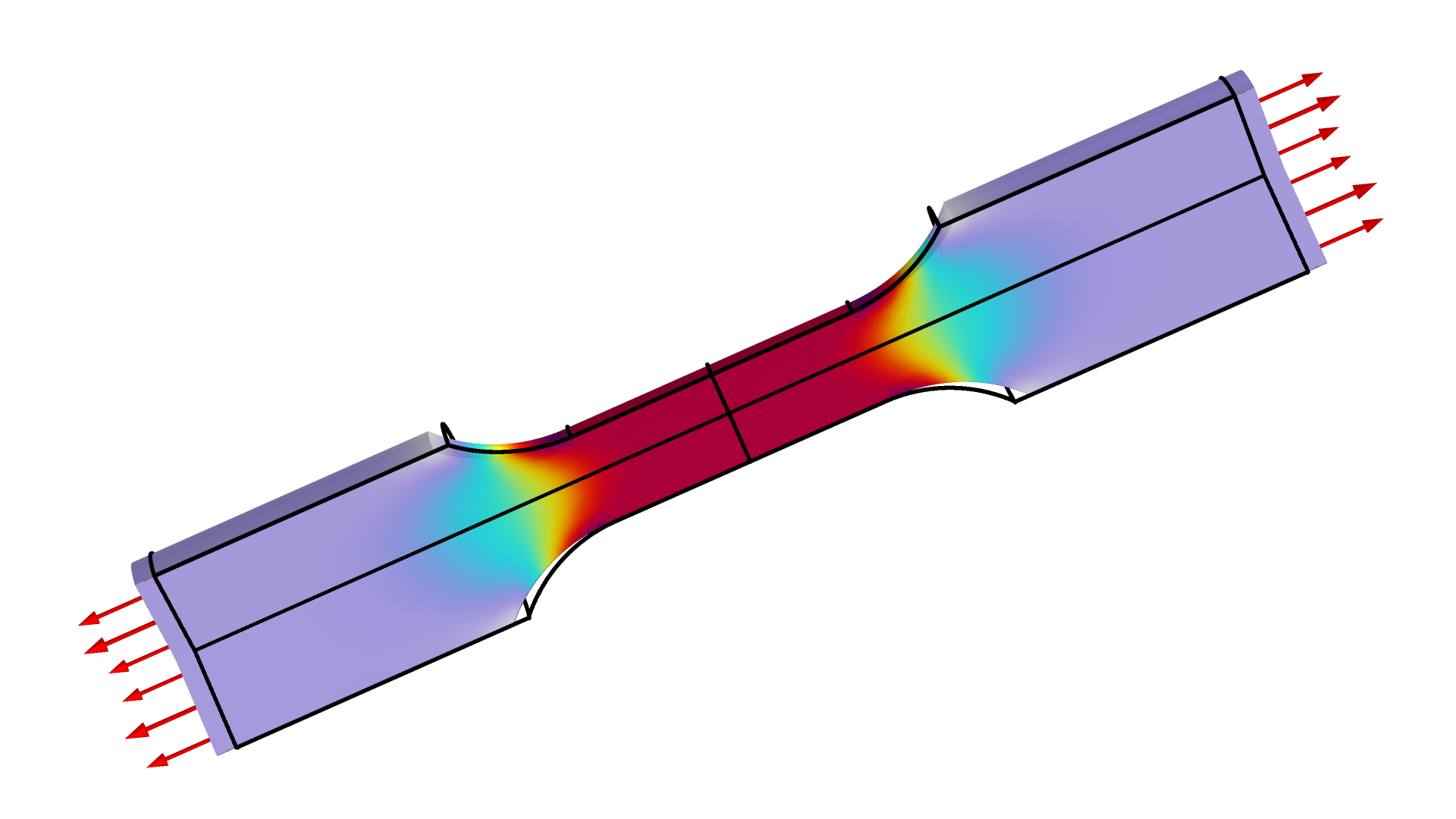
该图显示了拉伸试验的应力。力和中心径向位移被测量并表示为拉伸量的函数。
力和位移测量数据之间存在大约 10 个数量级的差异(SI 单位),所以使用常规的最小二乘法,我们需要调整最小二乘目标的权重来获得两个材料参数的准确结果。然而,我们可以通过两个测量误差 \sigma_F 和 \sigma_r 的标准差作为控制,使用最大似然法自动计算出最佳权重,即:
COMSOL Multiphysics 内置的最小二乘法目标法,让使用自定义目标来解决最大似然参数估计问题变得相当简单。COMSOL 案例库中提供的使用最大似然法进行参数估计模型,通过添加正态分布的噪点数据来生成合成数据。该模型在这些数据的基础上恢复材料参数和标准差,由此产生的力和径向位移如下图所示。
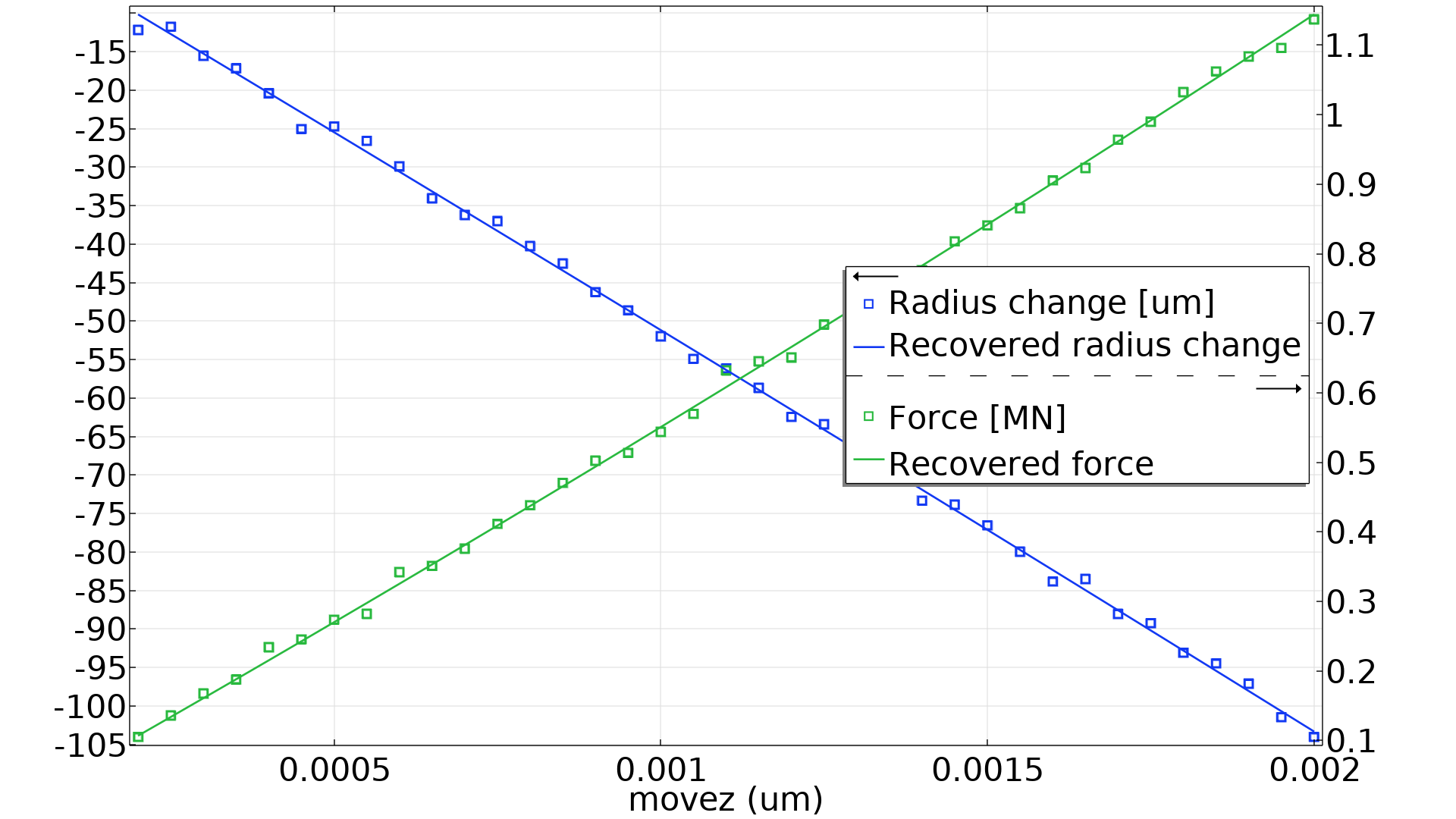
噪点数据和优化模型行为被绘制为拉伸量函数。两次测量都有 37 个数据点。
该模型能够将材料参数恢复到 0.1%-0.5% 的准确度和 6% 左右的标准差,预计准确度会随着测量次数的增加而增加。
在这篇博文中,我们只介绍了符合正态分布的噪点数据并且其标准差不变的情况,但最大似然参数估计还可以扩展到适合更多且更通用的情况,并且提取和估计信息时也能够保证数据的一致性和最优性。
自己尝试
单击下面的按钮,进入 COMSOL 案例库,自己尝试使用最大似然法进行参数估计模型。
更多资源
您还可以通过下面这些模型来探索更多参数估计的示例:
查看以下资源,了解有关参数估计的更多信息:



评论 (0)