在波动光学领域,很难用严格求解麦克斯韦方程的方法来模拟大型光学系统。这是因为在系统中出现的波需要通过足够精细的网格来分辨。COMSOL Multiphysics 软件中的波束包络法是解决这个问题的一种选择。在这篇博文中,我们讨论了如何使用 COMSOL 软件中的电磁波,波束包络 接口并处理一些限制。
比较求解大型光学模型的不同方法
在电磁仿真中,波长总是需要通过网格来解析以找到麦克斯韦方程的精确解。这一要求使得模拟比波长大的模型非常困难。对于光学简谐波问题,有几种方法可以处理大型模型。这些方法包括所谓的衍射公式,如夫琅禾费(Fraunhofer)、菲涅耳-基尔霍夫(Fresnel-Kirchhoff)和 瑞利-索末菲(Rayleigh-Sommerfeld)衍射公式,以及波束传播方法(beam propagation method ,BPM),如近轴BPM方法和角谱方法(参考资料1).
这些方法中大多数都使用亥姆霍兹方程的某些近似,并可以处理大型模型,因为它们是基于从一个平面中的已知场求解另一个平面中的场的传播方法。所以我们不必对整个域进行网格剖分,只需要为所需的平面使用二维(2D)网格即可。与这些方法相比,COMSOL Multiphysics 中的电磁波,波束包络 接口(文中简称“波束包络”接口) 在一个域中可以精确的求解亥姆霍兹方程。它可以处理大型模型,即如果满足一定的限制,可以大大放宽网格需求。

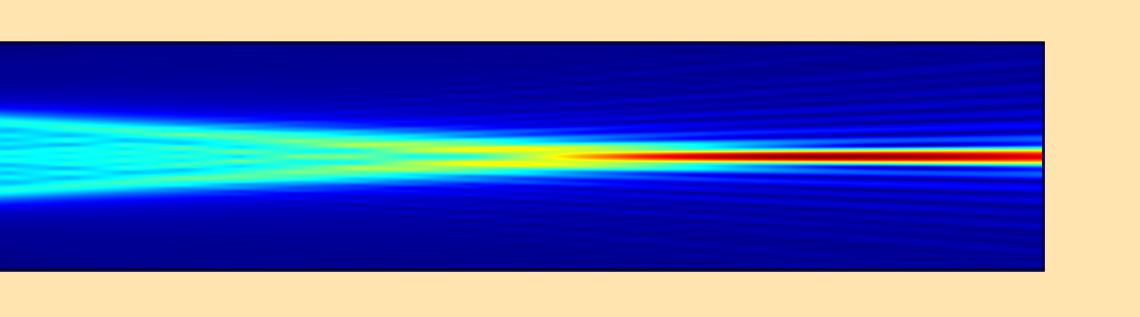
使用波束包络法模拟波长为1um的光经过透镜的聚焦效果。
下面,我们来讨论 波束包络 接口的更多细节。
波束包络的背景理论
我们来看看波束包络 接口背后的计算理论。如果将这个接口添加到模型中,单击 物理场接口 节点并将相位明细类型 变更为用户定义,我们将在方程 中看到以下内容:
其中,\bf E1 是求解的因变量,称为包络函数。
在场的相量表示中,\bf E1对应于振幅,\phi_1代表相,即
第一个方程是 波束包络 接口的控制方程,可以通过将第二个电场方程代入亥姆霍兹方程来导出。如果我们知道 \phi_1,唯一未知的是 \bf E1,那么我们可以就求解 \bf E1。为了解决这个问题,相 \phi_1 需要提前 给出。
对于第二个方程,我们先假设一种形式,可以将快速振荡部分(即相位)从场中分解出来。如果假设成立,那么包络 \bf E1 是“缓慢变化的”,所以我们不需要解析波长。相反,我们只需要求解包络的缓慢波动。这个过程使得我们在个人电脑上模拟大尺度波动光学问题成为可能。
这时,您可能就会问:“什么时候我们需要求解包络而不是场本身?透镜模拟就是一个例子。有时候你可能需要的是强度,而不是复杂的电场。实际上,强度由包络模的平方给出。在这种情况下,只要得到包络函数就足够了。
如果相函数未知会发生什么?
从光束包络法背后的数学原理又引入了更多的问题:
- 如果相 并不准确地 知道,怎么办?
- 这种情况下,我们可以用 束包络 接口吗?
- 结果正确吗?
要回答这些问题,我们需要多了解一点数学知识。
1D 示例
让我们举一个最简单的测试案例:一个平面波,Ez = \exp(-i k_0 x),其中 k_0 = 2\pi / \lambda_0 ,波长 \lambda_0=1um,它在 20um 长的矩形域中传播。(出于演示的目的,我们有意使用了一个较短的域。)
面外波从左边界进入,并无反射地穿过右边界。这可以在波束包络中 通过添加匹配 边界条件实现,其中左侧有激励,右侧无激励,同时在顶部和底部添加一个理想磁导体的边界条件(意味着我们不关心 y 方向)。
正确的相明细设置如下图所示。
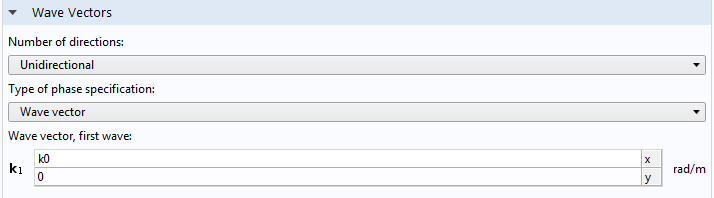
我们知道 Ez = \exp(-i k_0 x),其中相位函数 k_0 x 是或者波矢量是 (k_0,0) 已知的。把相位函数代入第二个方程,我们反过来得到 E1z = 1,常数方程。
求解一个常数方程需要多少个网格元素?只有一个!(见此前关于高频建模的博文。)
以下结果显示了包络函数 E1 的电场模 E, ewbe.normE,等于 |{\bf E1}|。在这里,我们可以看到,如果我们给定精确的相位函数,常数1,我们使用任意的网格数量均可以得到正确的包络函数,正如预期的那样。出于确认目的,E1z 的相位 arg(E1z),也在下图中进行了绘制。同样在意料之中,相位值为0。

正确相位函数 k 的电场 z 分量 (红色)、电场范数(蓝色)和包络函数的相位(绿色) 0x,针对不同的网格大小计算。
现在,让我们看看如果我们预先定义的相位函数有点偏离会发生什么——比如说,(0.95k_0,0) 而不是精确的 (k_0,0)。我们得到了什么样的结果?让我们来看看:

当相函数为错误的 0.95k0x 时,不同的网格数量下计算得到的电场 z 分量(红色)、电场模(蓝色)和包络函数的相位(绿色)
我们在这里看到的包络函数就是所谓的拍频。很明显,所有结果都取决于网格大小。为了理解发生了什么,我们需要一支铅笔、一张纸和耐心。
我们知道答案是 Ez = \exp(-i k_0 x),但我们在 COMSOL 软件中“有意”给出了一个不正确的估计。在第二个方程中代入错误的相位函数,我们得到 \exp(-i k_0 x)={\bf E1z} \exp(-0.95i k_0 x)。这导致 {\bf E1z}= \exp(-0.05i k_0 x),不再是常数1。这是一个波长为 \lambda_b= 2\pi/0.05k_0=20um 的波,称为拍频波长。
让我们看看上面六个网格时的结果图。我们得到正是期望的(红线),即 {\bf E1z}= \exp(-0.05i k_0 x)。绘图中自动取了实部,{\bf E1z}= \cos(-0.05 k_0 x) 。较低分辨率的图仍显示包络函数的近似解。这是有限元模拟的预期结果:更粗糙的网格给出更近似的结果。
这表明,如果我们对相位函数做出错误的猜测,我们将得到错误的包络函数。因为猜错了,包络函数加了一个拍的相位(绿线),就是 -0.05 k_0 x。
那电场模 \bf E, 呢?看上面图中的蓝线。看起来 COMSOL Multiphysics 得到了正确的ewbe.normE,仍然为常数 1。让我们计算一下:在第二个方程中代入错误的相位函数和错误的包络函数,我们得到 {\bf Ez}= \exp(-0.05i k_0 x) \times \exp(-0.95i k_0 x) = \exp(-i k_0 x),这是正确的结果!
如果我们考虑 \bf E的模,我们得到一个正确的解,常数1。这就是我们想要的。请注意,我们可能无法显示 \bf E,因为计算域可能太大,但我们可以通过粗糙的网格来分析和显示 \bf E 的模。
这并不是投机取巧。相反,我们看到,如果相位函数不正确,包络函数也将不正确,因为它变成复杂的拍频。然而,电场的模仍然是正确的。因此,为了获得正确的电场,正确计算包络函数是很重要的。以上情节清楚地表明。六网格情况给出了完全正确的电场范数,因为它完整解决了包络函数。其他网格根据网格大小给出包络函数的近似解。包括电场模。这是一个普遍的结论,适用于任意情况。
无论我们在 COMSOL Multiphysics 中使用什么相位函数,只要我们正确求解第一个方程,且相位函数在域上是连续的我们可以得到正确的 \bf E1,。当一个域中有多种材料时,相位函数的连续性对解的精度也很关键。我们可能会在未来的博客文章中讨论这个问题,但在之前的文章中也提到过关于高频建模的博文。
2D 示例
到目前为止,我们已经讨论了一个标量波数。更一般地,相位函数由波矢量指定。当波矢没有猜对时,就会产生向量值的后果。假设我们有与第一个例子相同的平面波,但是我们对相位做了错误的猜测,即,k_0(x \cos \theta + y \sin \theta) 而不是 k_0 x 。在这种情况下,波数是正确的,但波矢量是错误的。这一次,拍频发生在 2D。
让我们从执行与 1D 示例相同的计算开始。我们有 \exp(-i k_0 x)={\bf E1z}(x,y) \exp(-i k_0 (x \cos \theta+y \sin \theta) ) 包络函数现在被计算为 {\bf E1z}(x,y) = \exp(i k_0 (x (1\cos \theta) y \sin \theta) ) ,它是一种向 (1\cos \theta, -\sin \theta) 方向传播的倾斜波,k_b = 2 k_0/\sin (\theta/2) 波数,\lambda_b=\lambda_0/(2\sin (\theta/2))波长。
下图显示了不同的最大网格尺寸下, 入射角 θ=15° 时在 3.8637um x 29.348um 的域上的结果。使用了与前面 1D 例子相同的边界条件。唯一不同的是左边界的入射波是 {\bf E1z}(0,y) = \exp(i k_0 y \sin \theta) 。(注意我们要给出对应的错误边界条件,因为我们的相位假设是错误的。)
在最细网格(最右边)的结果中,我们可以确认 \bf E1z 就像我们在上面的计算中分析的那样计算被计算 \bf Ez 为常数1。这些结果与 1D 的例子一致。

错误相位函数的电场模(顶部)和包络函数(底部),针对不同的网格大小进行计算。颜色范围表示从 -1 到 1 的值。
使用波束包络接口模拟透镜
我们的最终目标是用波束包络接口模拟一束电磁波通过毫米量级光学透镜的结果。如何才能做到这一点?我们已经讨论了如何正确计算的方案。下面的例子是对曲率半径为 500um、折射率为 1.5 (焦距约为 1 毫米)的平凸透镜上入射光束的模拟。
在这里,我们使用 \phi_1 = k_0 x,这一点都不准确。在透镜之前的区域中,存在反射,这产生了干涉。在镜头里,有多次反射。在透镜之后,相位是球形的,因此光束聚焦成一个点。所以这个相位函数和镜头周围发生的情况相差甚远。

\bf E1z的结果图。插图显示了镜头内最细的拍波长。
从图中可以看出,镜头中出现了明显的波动(见插图)。
注意:从 5.5 版本开始过渡在透镜表面引入边界条件,以模拟抗反射涂层,从而消除由于反射而产生的拍频。(看到这个上一篇博文。还要注意,即使有抗反射涂层,网格细化也是必要的,因为它只适用于垂直入射。镜头边缘周围的场可能有一些跳动。
实际上,最好的拍波长是 \lambda_0/2 在镜头前。为了证明这一点,我们可以执行与前面示例相同的计算。最小的拍波长是由于入射光束和反射光束之间的干涉,但是我们可以忽略这一点,因为它对前向传播没有贡献。我们可以看到,网格没有解决镜头前的波动,但我们暂时忽略这一点。
在折射率 n= 1.5 的透镜中,反向光束的波长为 3\lambda_0/2,前向光束的波长为 2\lambda_0。这个我们也可以用和前面例子一样的方法证明。同样,我们忽略了反向光束。在结果图中,可以看到前向光束的拍频波长为 2\lambda_0。反向光束只是一小部分(大约 4%n=入射光束的 1.5 倍,因此不可见)。下图显示了用 10 个网格元素解析透镜内拍频的情况。
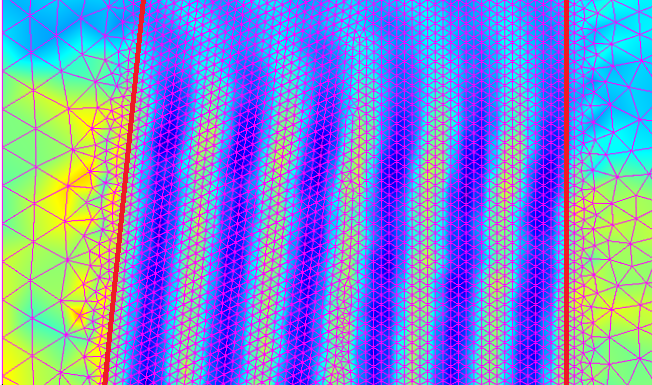
透镜内的拍波长。网格使用10个网格来解析拍频。
除了透镜中传播光束的拍频之外,后续空气域中的拍频相当大,因此我们可以在这里使用粗糙网格。这可能不适用于更快的透镜,它们具有更快的二次相位,并且可以具有非常短的拍频波长。在这个例子中,我们必须仅在透镜域中使用更精细的网格来解决最快的跳动。
计算出的电场模显示在这篇博文的顶部。为了验证这个结果,我们可以使用频域接口,然后使用菲涅耳衍射公式计算焦点处的场。电场模的结果非常一致。
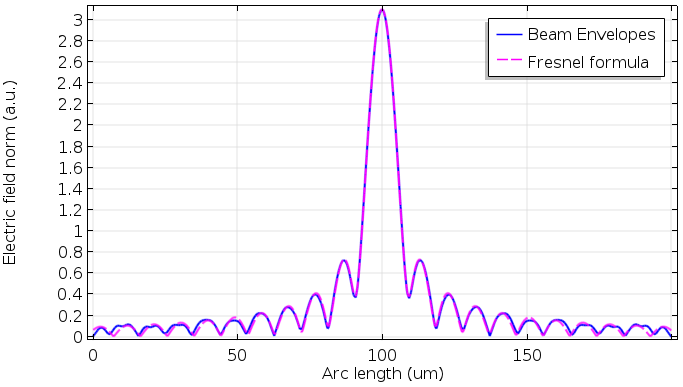
比较波束包络接口和菲涅耳衍射公式。该网格使用 10 个网格来解决透镜内的拍频。
下面的比较显示了网格大小的相关性。我们的使用 \lambda_b/6,等于 \lambda_0/3 得到了很好的结果。这使得更容易对透镜域进行网格划分。
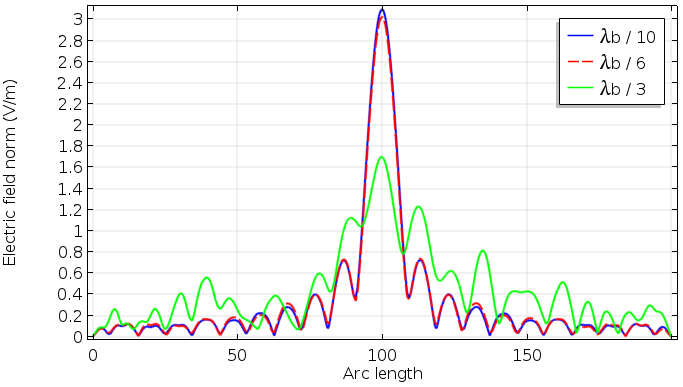
网格大小取决于焦点处的电场模。
从 COMSOL 软件的 5.3a 版本开始菲涅耳透镜教程模型包括使用波束包络接口。菲涅耳透镜通常非常薄(波长级)。即使在透镜内部或在表面不连续处及其周围存在衍射,透镜部分周围的细网格也不会显著影响网格元素的总数。
结束语
在这篇博文中,我们讨论了波束包络接口的背景知识,以及我们如何能获得波动光学问题的精确解。即使我们得到拍频,拍频波长也可以比波长长得多,这使得模拟大型光学系统成为可能。
虽然通过检查网格大小来解决拍品问题看起来很繁琐,但这并不仅是波束包络 接口需要的工作。当我们使用有限元方法时,我们总是需要检查精确计算的解与网格大小的相关性。
后续步骤
自己尝试:点击下面的按钮下载毫米波范围焦距透镜的模型文件。
参考资料
- J. Goodman, Fourier Optics, Roberts and Company Publishers, 2005.





评论 (2)
进哲 李
2022-10-23老师您好,请问如何设置自定义入射光束(例如平顶光束)。或者高斯光束如何转化设置为平顶光束呢
Min Yuan
2022-11-09 COMSOL 员工您可以将高斯分布表达式替换为一个if算子实现平顶光束的设置,即满足某范围时,场幅值为某定值,否则为原本高斯光分布。