强制约束中数值问题的处理方法

在本系列博客的第一部分，我们讨论了如何通过简单的边界条件解决变分问题。接下来，我们将进行更复杂的约束，并使用拉格朗日乘子建立等效无约束问题。今天，我们讨论约束执行的数值问题。拉格朗日乘子法在理论上是精确的，但是在数值解的应用却有一定的挑战性。为了应对这个挑战，我们提出了 2 种缓解策略：罚方法和增广拉格朗日法。

对全局约束使用拉格朗日乘子法

假设一条指定长度的均匀悬链线的形状为 u(x)，悬挂在其自身重量下的单位长度的密度均匀的悬链线使函数值最小

 
如果约束仅是边界条件，则可以自由调整悬链线的长度，以获得满足最终条件的最低势能。但是，如果我们要求悬链线具有指定的长度 l，于是就增加了全局约束

 
如本系列博客的第二部分中所讨论的，对于拉格朗日乘子，该约束最小化问题可以转化为具有新自由度的无约束最小化问题。

 
请记住，全局约束中每个约束都具有单个拉格朗日乘子，而不是分布式（逐点）约束那样的字段。我们使用下式对此进行概括。

 
通过将一阶变分导数 u(x) 和 \lambda 都设置为从 \mathcal{L}
[u(x),\lambda] 到0，来推导一阶最优条件。有关变分导数的更多信息，请参阅读本系列博客的第一部分。

 
现在，我们来求解悬链线的形状，该悬链线分别悬挂在两个高 10 m和 9 m，相距 10 m的杆上，悬链线长 10.5 m。

两端狄利克雷（Dirichlet）边界条件也可以使用自己的拉格朗日乘子作为约束添加。在本系列博客的第二部分中，我们演示了如何执行此操作。本文中，我们主要讨论全局约束，使用内置的狄利克雷边界条件 节点来固定端点。

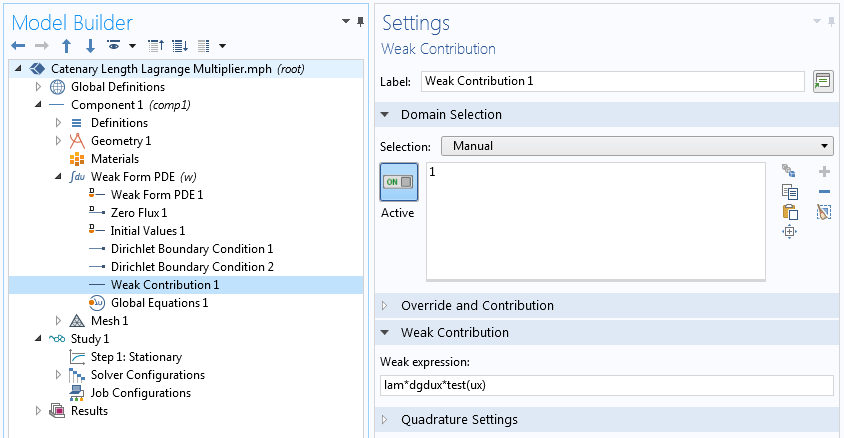
全局约束设置。

请注意，在上述弱贡献中，不包含 \frac{\partial g}{\partial u} 项，因为 g 只是 u^{\prime} 的函数并不是 u 的函数。

此时，尝试计算求解会生成错误消息。这是由当使用拉格朗日乘子法求解含全局约束或分布约束的非线性问题时一个常见数值问题引起的。对于一些试验解，有限元刚度矩阵（Hessian矩阵的优化）可以是单一的。因此，良好的初始值很重要。

应对该挑战的一种常用方法是将无约束问题的解用作约束解的初始估计。在 COMSOL Multiphysics® 软件中，这可以通过在同一研究中添加两个步骤并禁用第一个研究中的约束来实现。第一步的解将自动用作第二步的初始迭代。

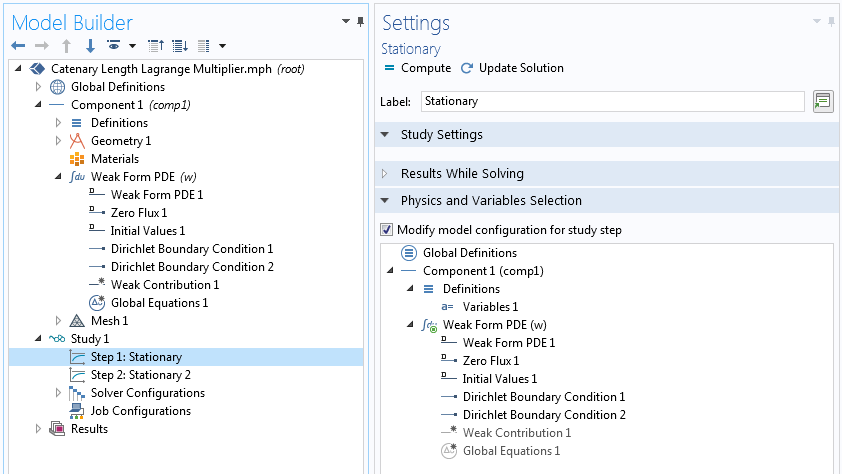
使用无约束解作为约束问题的初始估计。

限定长度以及无约束的悬链线。

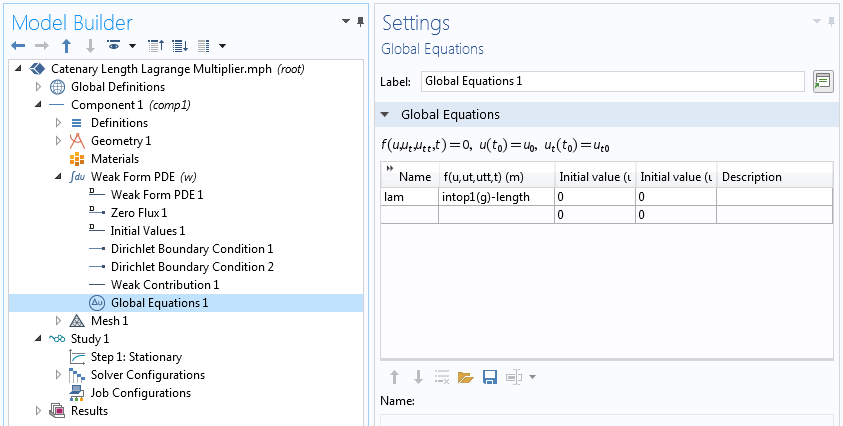
如果我们在结果 > 派生值>全局计算 中计算intop1（g），则该长度恰好为 10.5 m。拉格朗日乘子也可以在全局计算 中使用。原则上，此拉格朗日乘子与我们必须施加的张力有关，以使其维持所需的长度。

拉格朗日乘子的另一个常见数值问题是刚度矩阵中的正定损失。许多不受约束的变分问题都有正定刚度矩阵。此时，可以利用正定性的迭代线性求解器。使用拉格朗日乘子法执行约束会导致鞍点问题，并且相应的线性系统是不确定的。这个问题并不是不可以解决，我们可以使用直接求解器，但计算成本会很高。

我们已经设计出多种方法来避免在全局和分布式约束中拉格朗日乘子的数值缺点。在这里，我们只讨论 2 种使用最广泛的方法：罚方法和增广拉格朗日乘子法。

罚方法

约束最小化问题的惩罚性表述将拉格朗日乘子项替换为惩罚约束违反的项。在全局约束的情况下，罚目标函数为

 
如果罚因子太大，则上式中的第二项会使罚项太大，以至于对最小化总函数而言，满足约束条件非常必要。采用约束违反的平方，以便对长度的下冲和上冲都进行惩罚。因此，这是一个双向约束。相反，不平等约束是单向的。

在这里，罚因子是我们选择的，u(x) 是唯一未知的。因此，一阶最优条件变为

 
与拉格朗日乘子法相比，我们可以看到这种方法类似于用比例常数乘以约束违反来近似拉格朗日乘子。

 
如果我们将拉格朗日乘子视为维持约束所需的力，则罚方法提供了一种线性跳跃，当违反约束时会向后推，并确定跳跃常数。例如，如果我们的约束是温度，则罚方法将提供与试验温度和指定温度之差成比例的热通量，然后确定传热系数。

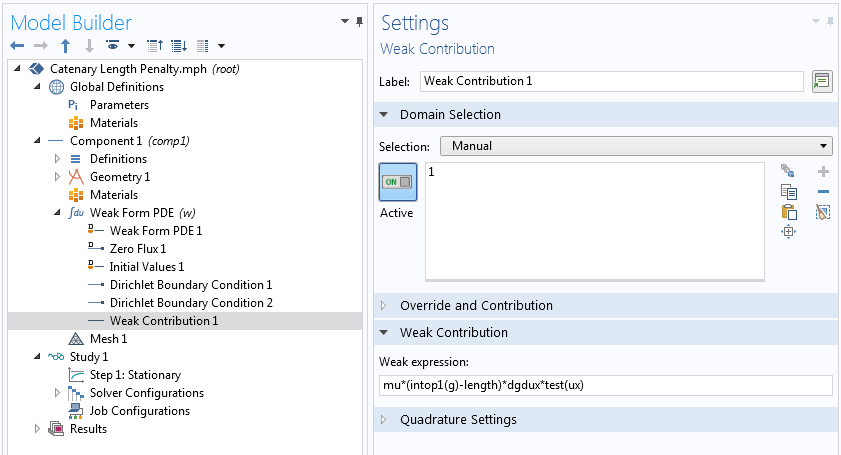
全局约束的罚执行示例。

罚方法易于实现，并且具有吸引人的数值特性。如果不受约束的刚度矩阵是正定的，那么它不会增加新的自由度并能保持刚度矩阵的正定性。但是，它也有缺点。例如，不能完全满足约束条件。为此，我们需要将罚参数设为无穷大，但是这无法在在数值上实现。实际上，一个有限但很大的罚项会使数值问题陷入困境。此外，非常大的罚参数使解过于关注可行性，而以最优性为代价。因此，诀窍是找到一个足够大的罚参数，以更好地近似约束条件，但又不要太大。

下面，我们看看罚参数的各种值对长度约束的满足程度。

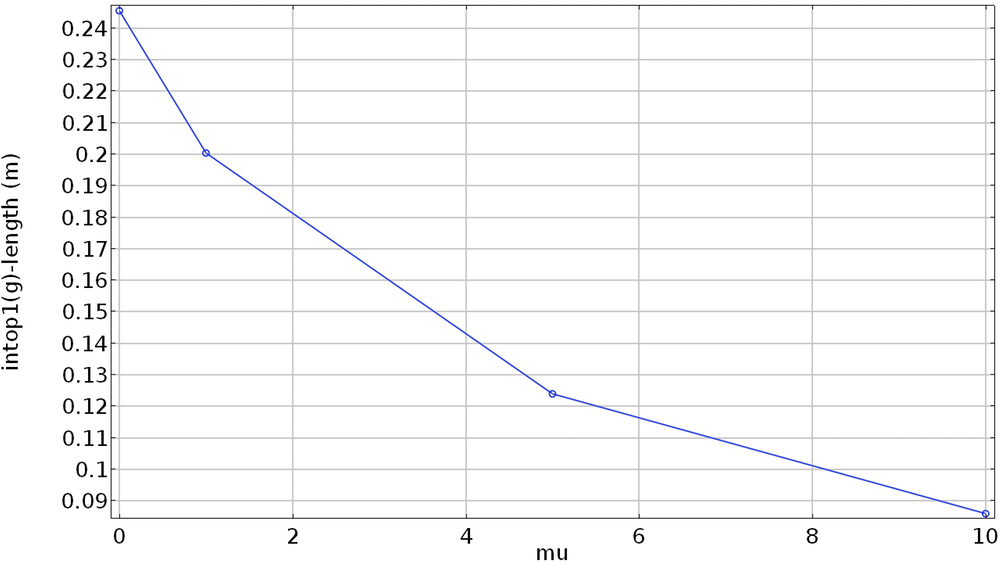
如果罚参数较高，则计算出的长度和指定长度之差将趋近于零。

从上图可以看出，罚因子越高，强制约束越好。但是，如果我们将罚因子设置为20，则会由于惩罚因子太高而出现收敛误差。

罚参数的辅助扫描

我们已经开发了一些算法来逐渐改善罚问题。一种简单的算法是逐渐增加罚因子，同时将之前罚参数的收敛解重新用作初始估计。

近似拉格朗日乘子包含约束违反和罚项的乘积。这样，当约束违反较小时，我们可以承受较大的罚参数，而不会使数值问题变得不适。因此，如果我们从其解近似满足约束条件的试验解开始，则可以使用更高的罚因子（与大量违反约束条件的试验解相比）。通过在罚参数上添加辅助扫描，可以轻松地在 COMSOL Multiphysics 中实施该策略。

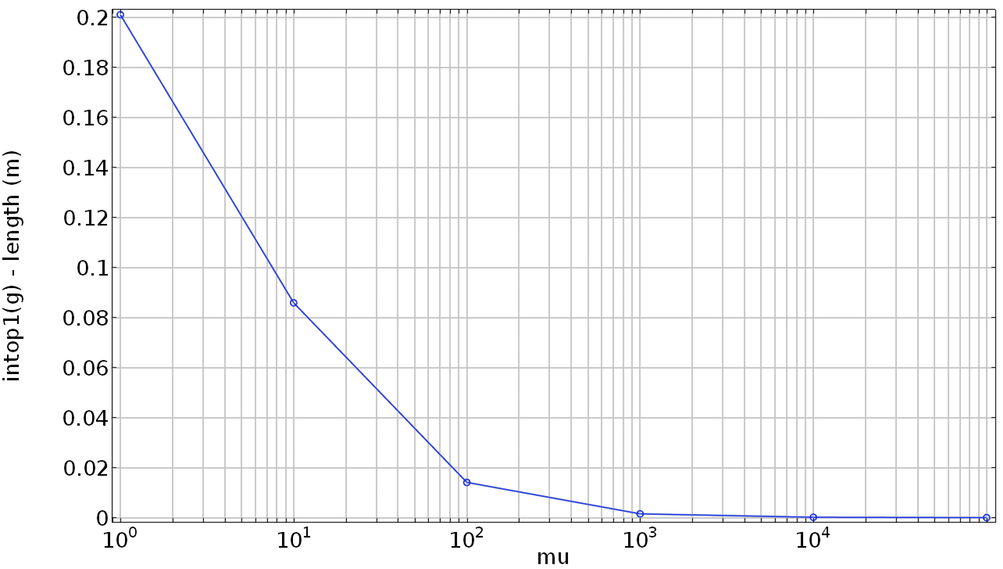
当使用辅助扫描罚因子时，计算长度与指定长度之差与罚因子之比。

如上图所示，对罚因子进行辅助扫描使我们能够使用更高的罚因子而不会产生不良情况，更重要的是，可以更好地执行约束。下图比较了这些连续解和拉格朗日乘子解的精确度。

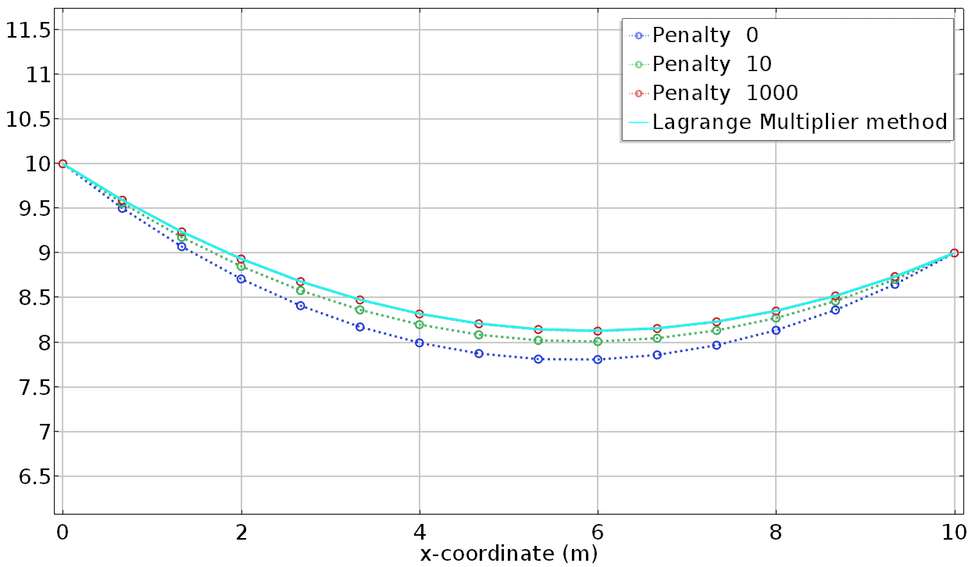
罚和拉格朗日乘子解的比较。

增广拉格朗日法

为了结合罚方法和拉格朗日乘子法的优点，同时避免它们的缺点，我们设计了增广拉格朗日法。为了清楚起见，我们从微积分问题开始。

对于问题

 
拉格朗日乘子法可求解无约束问题

 
而罚方法使用

 
增广拉格朗日法同时具有拉格朗日乘子和罚项。

 
在拉格朗日乘子法中，拉格朗日乘子为未知数；而在增广拉格朗日法中，从拉格朗日乘子的估计开始，对其进行迭代改进。

拉格朗日函数的一阶最优条件是

 
将其与拉格朗日乘子法的最佳条件进行比较，可以看出乘子的改进估计为

 
回到我们今天讨论的变分演算和全局约束，增广拉格朗日迭代为

 
该迭代将继续进行，直到约束违反足够小（或等效，直到乘子停止明显变化）为止。初始拉格朗日乘子通常为零。请记住，解也由指引。上述方程式忽略了该值，以将注意力集中在拉格朗日乘子更新上。

通过在拉格朗日乘子中逐步积累越来越多的力（通量），增广拉格朗日方法可以很好地实施约束，同时保持较小的罚参数。增广拉格朗日法对于分布式约束特别有吸引力，因为每个点都可以根据局部条件进行不同的更新。

罚方法（不按顺序增加）和增广拉格朗日法是 COMSOL Multiphysics 中用于接触约束的内置方法，但是接触力学涉及不等式约束。在本系列博客的下一篇博客文章中，我们将展示如何在相应物理场中没有内置功能的情况下添加用户定义的不等式约束。

故意违反约束

有时我们想故意违反约束。假设在上面的示例中我们将长度约束设置为 10.04 m。这在物理上是不可能的，因为支座之间的最短距离（直线距离）为 10.05 m。

拉格朗日乘子法想要精确地执行约束，因此，这将导致收敛问题。但是，我们可能仍想在某种程度上违反约束条件来获得不精确的解。在这种情况下，约束不一致或存在多余约束时，拉格朗日乘子法就无法收敛。但是，我们可以使用近似约束方法（例如罚方法和增广拉格朗日法）来放宽约束并获得近似解。例如，多体动力学模块为关节提供了一种内置的罚方法，以使模型对过度约束不那么敏感。

后续操作

今天，我们已经证明了拉格朗日乘子法可以有效的正常工作。但是，它对解的初始估计更敏感，并且可能使不确定的潜在问题变得不确定，因此必须使用直接求解器。罚方法和增广拉格朗日乘子法克服了这些困难，以换取一些对约束的违反。

我们希望可以精确地执行约束，但是在约束不一致或过多的问题中，我们可能希望不精确地强制执行约束以获得一些近似解。在下一篇博客文章中，我们将讨论不平等约束。拉格朗日乘子法还会产生不平等约束的缺点。

本系列博客，我们更多的介绍了罚方法，并集中讨论了一维和单个未知问题。在即将发布的另一篇博客文章中，我们将讨论多个维度、多个字段和高阶导数。

单击下面的按钮联系 COMSOL ，了解有关 COMSOL Multiphysics 中基于方程的建模功能的更多信息。

查看更多有关“变分问题和约束”问题的系列博客文章

• 第1部分：皂膜仿真和其他变分问题
• 第2部分：指定变分问题的边界条件和约束
• 第4部分：强制执行不等式约束的方法
• 第5部分：图像去噪及其他多维变分问题