使用 COMSOL Multiphysics 模拟直线电机或发电机

“AC/DC 模块”中的旋转机械，磁场物理场接口可用于模拟旋转机械，如电动机或发电机。利用磁场和移动网格这两个物理场接口模拟直线设备或管式设备时，定制的线性周期性边界条件是非常适合的。在本篇博客文章中，我们将探索如何定制线性周期性边界条件，并模拟用于波浪能的管式发电机。

直线电机或发电机

直线电机 (LEM) 是一种能进行直线运动的机电设备，无须使用任何机构它就能将旋转运动转换为直线运动。直线电机和旋转电机相似，定子和转子沿径向平面被切割并展开以提供线性推力。相同的电磁力在旋转电机中产生扭矩，在直线电机中则产生直接的线性力。

值得一提的是，“AC/DC 模块”中的旋转机械，磁场接口包含模拟旋转机器所需的所有功能部件。该接口结合了磁场接口；磁场，无电流接口和移动网格接口。经定制后此接口适用于模拟旋转机器，由此极大地简化了静态域和旋转域的定义，以及两者之间接口的处理。在模拟模型的扇形区域或某一部分以获得完整设备的仿真结果时，扇区对称和周期性边界条件这样的功能部件也极其有用。尽管该接口显著减少了建立旋转运动模型所需的工作，但直线运动中不能使用该接口。

下面，我们将演示如何对磁场和移动网格这两个物理场接口定制耦合来模拟管式发电机。另外，还会解释如何创建线性周期性边界条件，这是利用广义拉伸算子模拟直线/管式电机或发电机的一个重要元素。

用于波浪能转换系统的管式发电机

管式电机在许多应用中受到青睐，从车辆的主动悬架系统到潮汐能和波浪能转换系统都有涉及。管式电机的传输效率比传统的直线和旋转转换系统高出许多，因为推力直接作用于负载。管式电机的另一个优势是，没有定子端部绕组。因此，铜损相对较少，永磁材料的利用率很高。

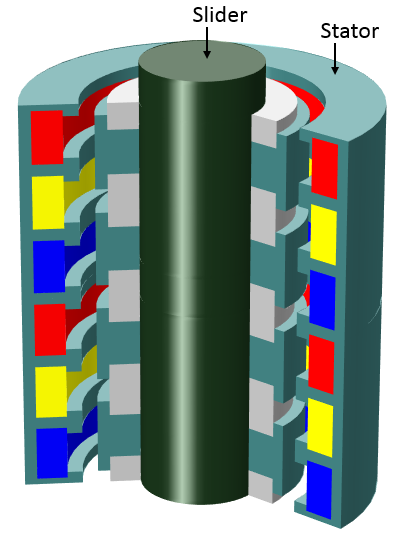
下面，我们将讨论对管式发电机进行模拟的技巧（如下图所示）。管式发电机包含两个主要零件：一个静态定子和一个作直线移动的滑块。定子由三相绕组和一个非线性磁芯构成。滑块由轴、永磁体及永磁体之间的非线性磁性材料构成。

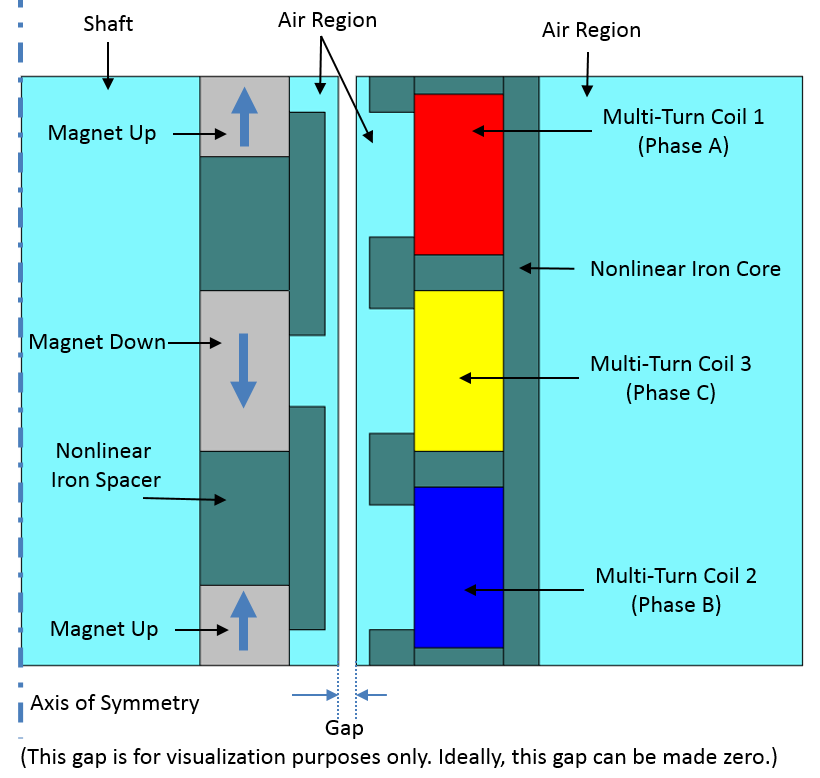
左图：管式发电机的三维视图。右图：管式发电机的二维轴对称视图。该视图详细展示了线圈、永磁体及非线性磁性材料的分布。

使用 COMSOL Multiphysics 模拟管式发电机

利用磁场和移动网格物理场接口，我们可以在 COMSOL Multiphysics 中模拟上方描述的管式发电机。该模型绕机器轴对称，因此在二维轴对称域建立模型。几何已完全参数化，因此如果需要，该模型可用于优化研究或参数化扫描研究。参数已定义在全局定义>参数下，如下方屏幕截图所示。可以从案例下载中下载这里描述的管式发电机示例。

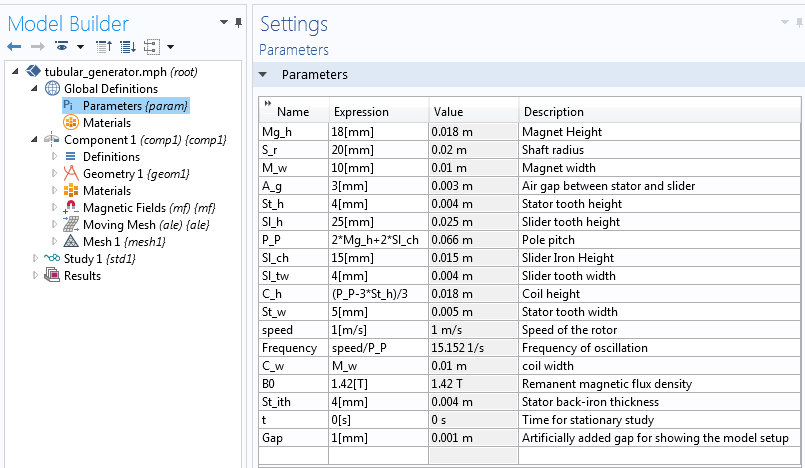
建立管式发电机模型所用的参数列表。

该模型几何旨在将定子零件和滑块零件创建为独立的几何体。随后这两个零件通过形成装配组装完成，由此在该接口中，定子和滑块间自动创建了一致对。同时添加移动网格，以模拟滑块的运动。

注：这里，我们在定子和滑块间添加了 1 毫米的额外间隙。由此重叠边界清晰可见，以应用定制的线性周期性边界条件。这条间隙纯粹为增强可视化效果而建，不会对结果（即电压输出或电磁力）产生任何影响。

物理场 I：磁场

磁场接口用于模拟管式发电机的电磁场。定子和滑块中的非线性材料使用“安培定律”节点进行模拟，同时“本构关系”设置为“H-B 曲线”。

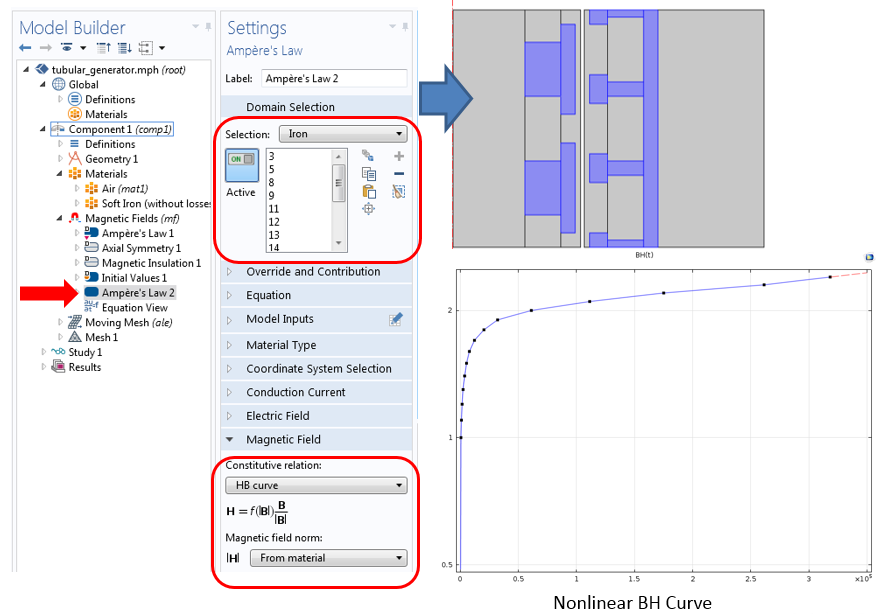
设置“安培定律”节点，描绘非线性磁性区域 “H-B 曲线”的实现。

三相绕组使用磁场接口中的多匝线圈功能部件进行模拟。三个相位的设置都相同。下方仅显示第三相的设置。每个相位的绕组包含 100 匝金属线，截面积为 1e-6[m^2]，电导率为 6e7 s/m。三个相位都设为开路（即零电流），以计算线圈中的感应电压。

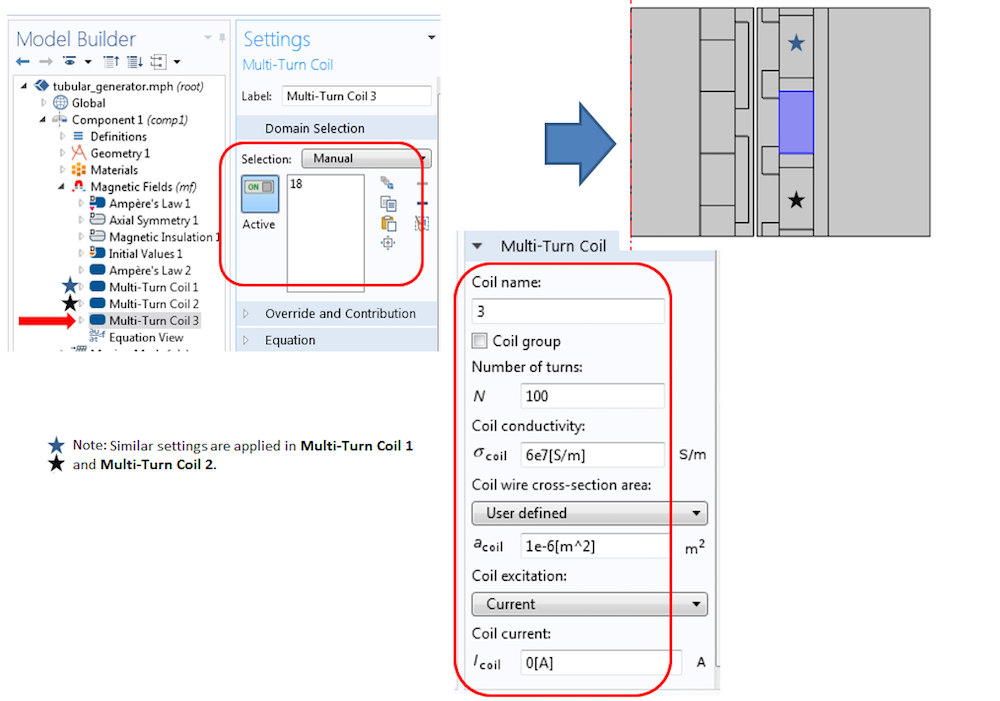
“多匝线圈”功能部件显示开路设置，以及匝数、电导率和横截面积。

滑块中的永磁体使用“安培定律”节点模拟，“本构关系”设为“剩余磁通密度”。添加了两个独立节点，一个表示磁体指向上方，一个表示磁体指向下方。下图仅描述磁体指向下方的设置。

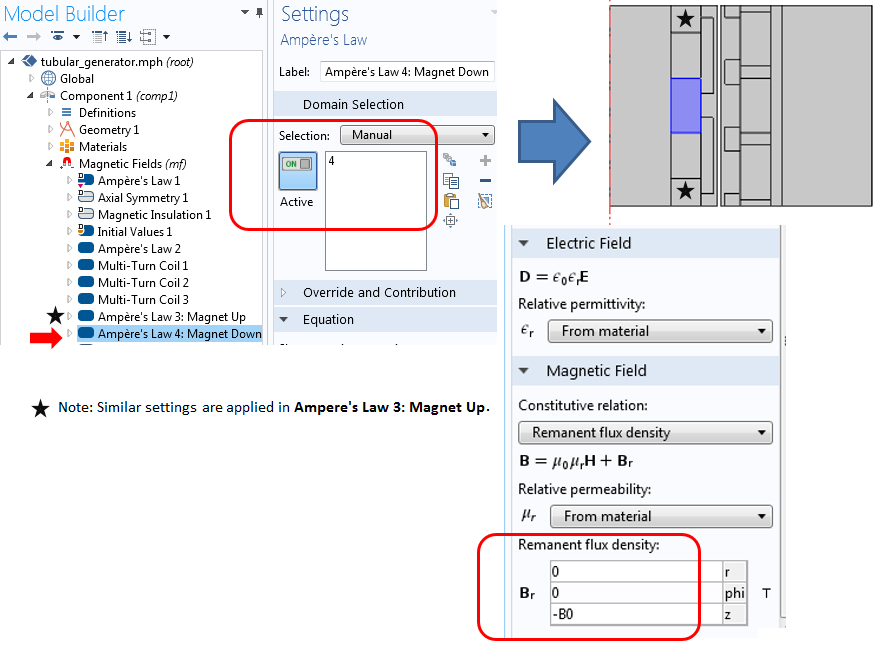
模拟永磁体的“安培定律”节点设置。

因为我们要求解的仅是管式发电机的一部分，所以必须在定子侧和滑块侧中的任一侧应用适当的周期性边界条件。在这里，适当的周期性条件指的是连续性条件。

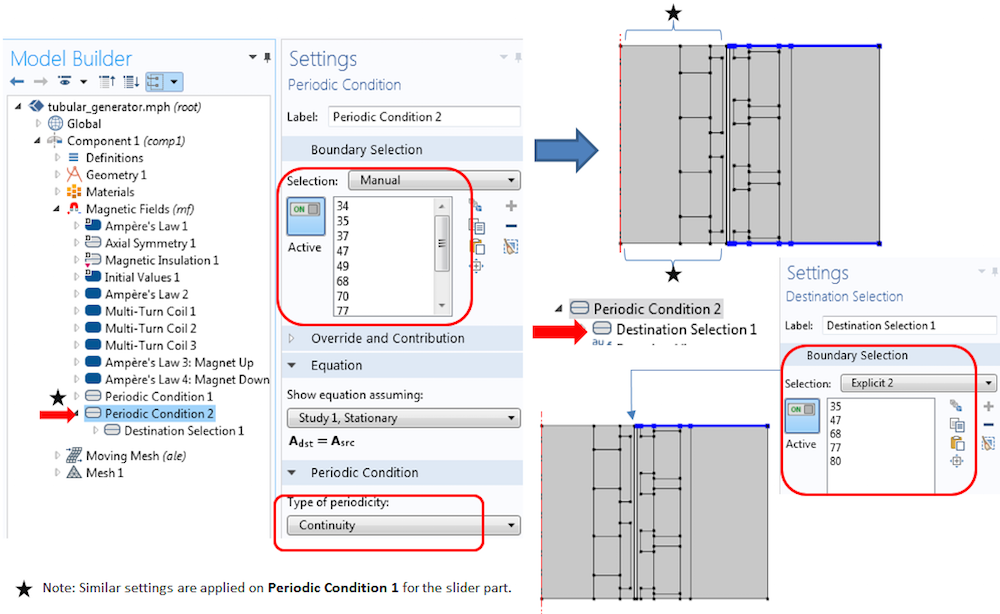
定子侧的连续周期性边界条件设置。相似的设置也适用于滑块侧。

定制线性周期性边界条件

旋转机械，磁场接口已包含扇区对称功能部件。使用此功能部件时，仅需模拟旋转机器的一个扇区就能获得整个设备的仿真结果。注意，“扇区对称”功能部件仅适用于旋转机器，不可用于作直线运动的电机或发电机。

要构建如上定制的线性周期性边界条件，需要再执行几个步骤。首先，必须创建角频率与发电机相同的锯齿波波形。在组件 1 > 定义 > 波形 1 下创建。下方屏幕截图显示锯齿波波形的其他设置。

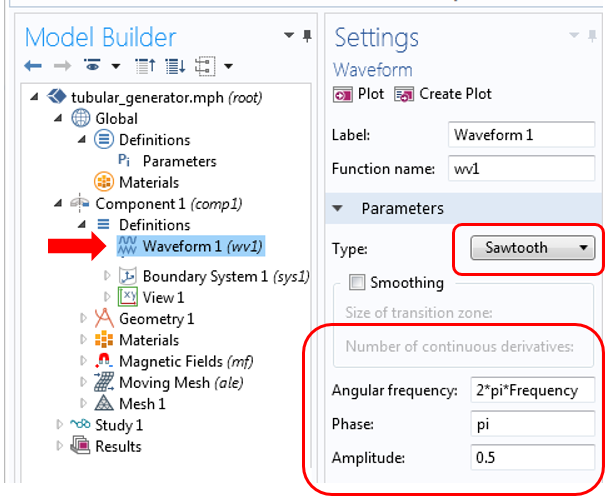
模拟发电机角频率时的锯齿波波形设置。

上方添加的锯齿波波形用于创建和锯齿波波形相似的解析函数，但偏移量大小为 0.5。解析函数添加在组件 1 > 定义 > 解析 1 下。

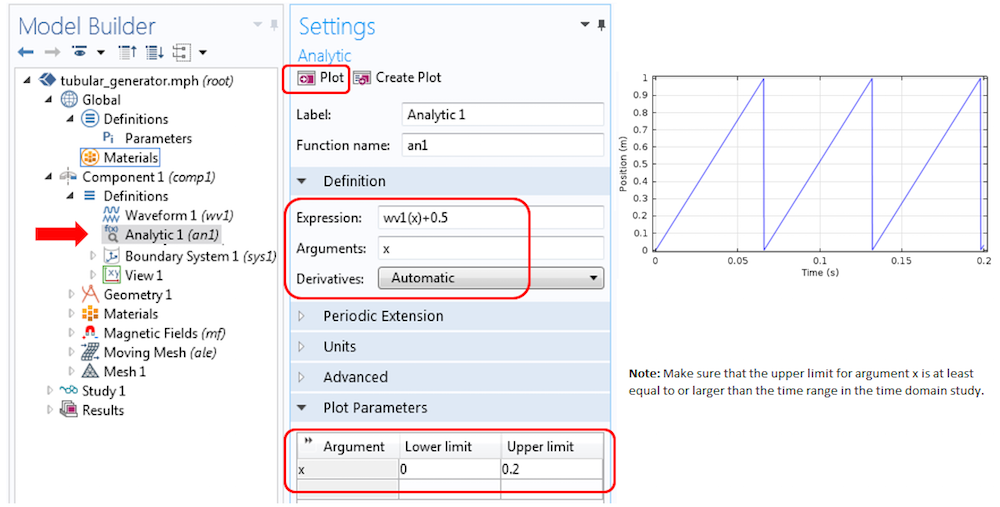
解析波形的设置和所得的波形绘图。

在一致对（定子和滑块间常见的一种边界）处，应当对因变量（矢量势，Az）添加连续性。因为定子是静止的而滑块按一定频率运动，所以需要定制此连续性条件以反映定子和滑块的线性周期。为此，使用“广义拉伸”算子映射定子到滑块的物理场。

定子边界 33 用作“广义拉伸”算子的源边界。其他设置如下所示。

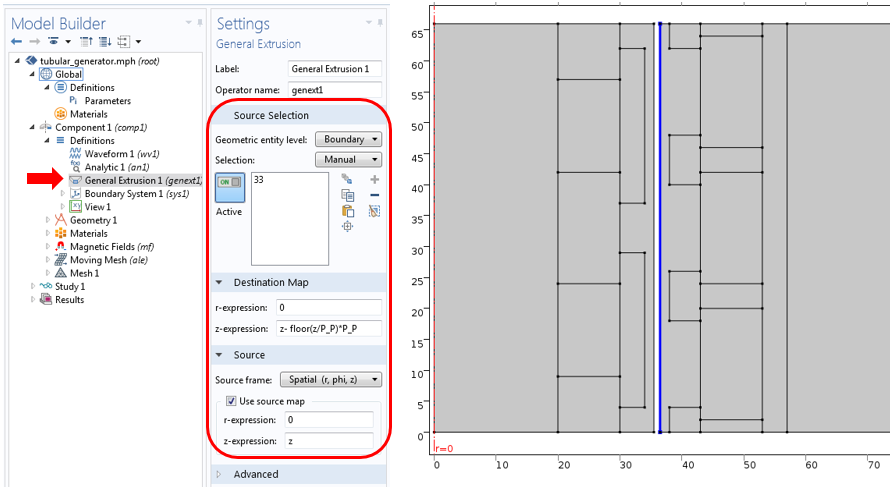
定子边界上定义的“广义拉伸”算子的设置。仅映射了 z-表达式的数据。

下面准备在常见边界上应用周期性连续性边界条件。为此，需要映射定子边界到滑块边界的矢量势。在边界 32 上添加“磁势”边界条件。

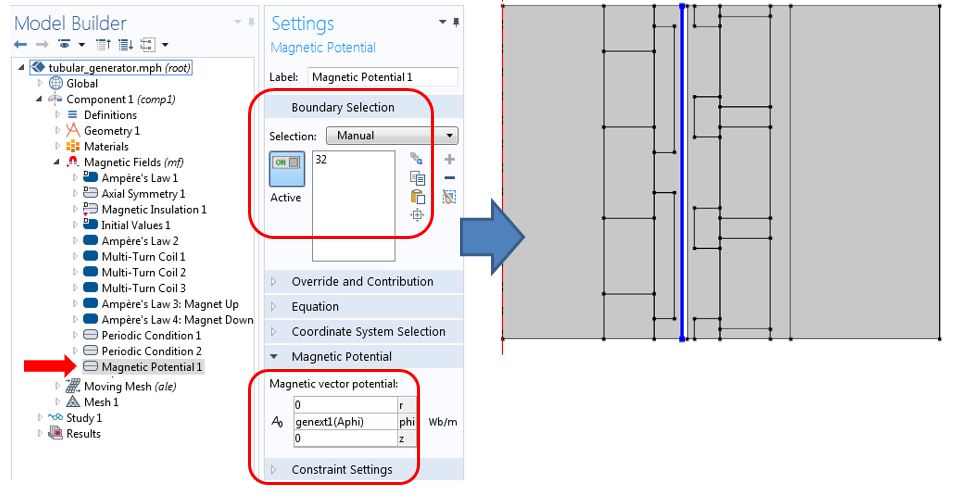
使用“广义拉伸”算子映射定子边界到滑块边界的矢量势。

为完成电磁场建模，需要在定子边界上添加“完美磁导体”边界条件。它表示电流的镜像对称平面。“完美磁导体”边界条件使磁场垂直于边界，并使边界上没有切向分量。

有兴趣学习“完美磁导体”边界条件以及磁场接口中其他相关边界条件的更多内容吗？请查看我们的博客文章“利用对称简化磁场模拟”。

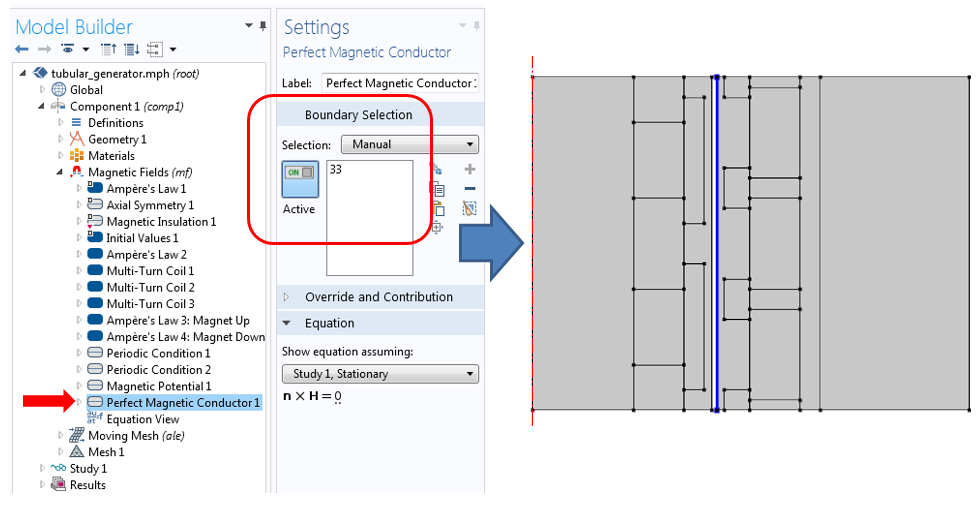
定子边界上“完美磁导体”边界条件的设置。

注：要模拟任何直线机器（即直线感应电机/发电机或同步电机/发电机），可以使用本文讨论的相同技巧来定制连续性边界条件，以施加线性周期性。尽管该方法同样适用于二维和三维轴对称几何，但对三维几何来说更复杂一些。在本篇博客文章中，我们不讨论定制的三维线性周期性边界条件。

物理场 II：移动网格

为模拟直线运动，先要添加移动网格接口。对定子域（及该侧的空气域）指派一个固定网格。同时使用 z-向的指定变形以及上一个解析函数定义的指定运动来模拟滑块部位。

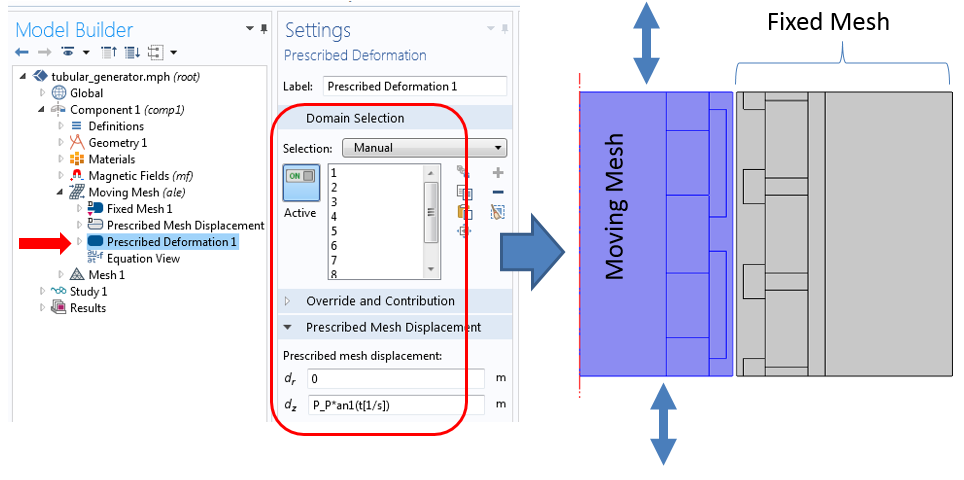
模拟管式发电机时使用的移动网格物理场接口及其关联功能部件设置。

网格剖分：在应用周期性边界条件的边上，源边和目标边所含网格数应当相同。为此，需要应用复制边功能部件。另外，对已设置了手动连续性边界条件的边界，“广义拉伸”算子可对其应用较细化的网格。

求解器设置和仿真结果

要设置正确的求解器以获得仿真结果，需要注意以下几点。首先，添加“稳态”研究步骤，以计算静态永磁体内部和周围的矢量势场。此静态解用作初始条件后，接下来求解“瞬态”研究步骤。这一步计算由作直线移动的滑块和三相线圈中的感应电压而产生的瞬态响应。因为该问题已在时域中求解，且模型中包含了非线性磁性材料，因此必须对非线性瞬态求解器作微调。非线性求解器的设置与这一技术支持知识库条目中建议的设置相似。

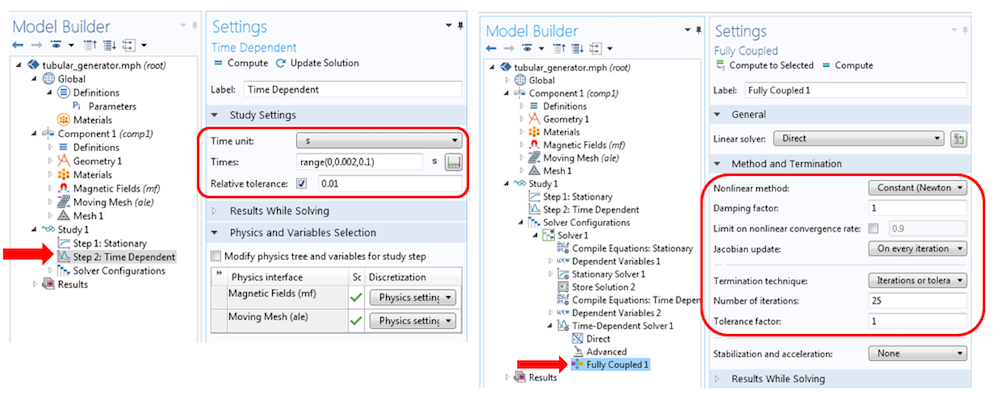
管式发电机的非线性求解器设置。该模型求解用时 0.1 s。

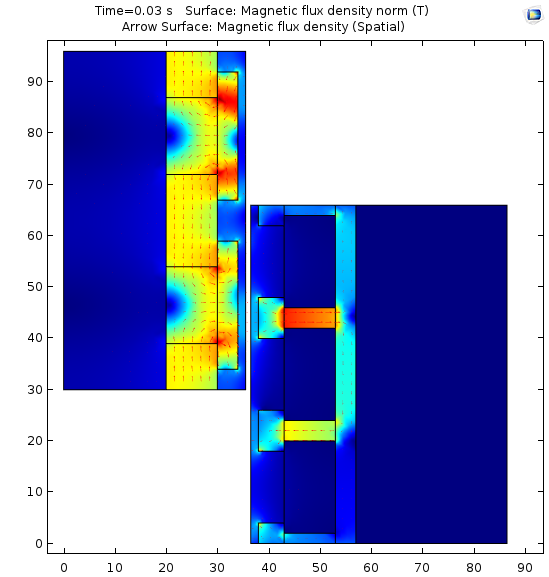
左图：t=0.03 s 时磁通密度的二维轴对称表面和面上箭头图。右图：t=0.1 s 时旋转三维几何上的磁通密度表面图。

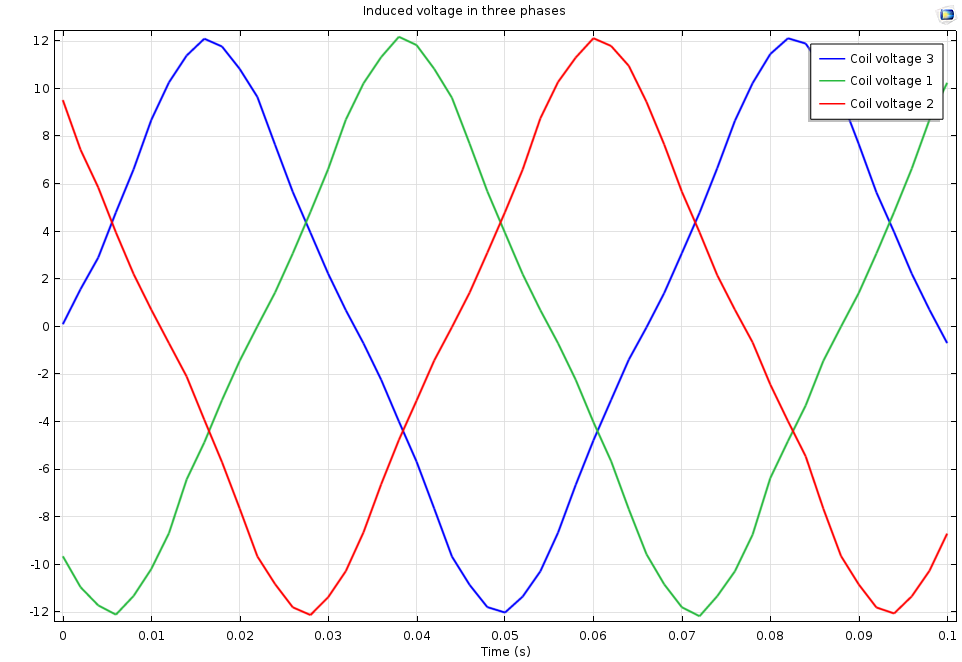
三相定子多匝绕组中开路感应电压随时间变化的图。

结束语

现有的旋转机械，磁场接口能求解对旋转机器的模拟。但在模拟直线电机或管式电机时，磁场和移动网格这两个物理场接口更适合。

今天，我们已经演示了如何使用“广义拉伸”算子定制线性周期性边界条件，以及如何模拟用于波浪能发电的管式发电机。上面展示的技巧同样适用于模拟各种直线电机。

自己动手尝试

• 下载教程模型：管式永磁发电机