使用 COMSOL Multiphysics® 模拟磁悬浮轴承

磁悬浮轴承广泛用在各种工业应用中，比如发电、石油提炼、涡轮机械、泵机和飞轮储能系统。和机械轴承不同的是，这类轴承是利用磁悬浮而非物理接触来支承移动载荷的。由于磁悬浮轴承运行时不产生摩擦且无需润滑，维护费用也低，因此正逐渐取代机械轴承，更何况这种轴承的使用寿命还更长。现在我们一起来了解如何使用 COMSOL Multiphysics® 软件计算磁力、扭矩和磁刚度等设计参数。

磁悬浮轴承的类型

根据工作方式的不同，磁悬浮轴承 可以分为两种类型：有源磁轴承（AMB）或无源磁轴承（PMB）。有源磁轴承依靠铁磁材料和电磁体（线圈和铁芯）之间的吸引力起作用。无源磁轴承依靠永磁体（PM）之间和/或传导面与永磁体之间的排斥力起作用。

有源磁轴承

有源磁轴承 由一个静止零件定子 和一个旋转零件转子 构成，定子包含电磁体和位置传感器，转子围绕轴旋转。在正常工作条件下，最理想的情况是，转子位于中心，与定子相隔一定的间隙，且间隙长度相等。不过，在遇到干扰时，转子的位置会受控于一个闭环反馈系统。传感器测量出转子的位置发生变化，随后将之传送到数字控制器。数字控制器处理好数据后，将信号传送给功率放大器。后者重新调整电磁体的电流，推动转子回到原来的位置。为了重新调整转子，设计人员必须要知道转子处于不同偏移位置时的磁力以及相应的电流，这一点很重要。

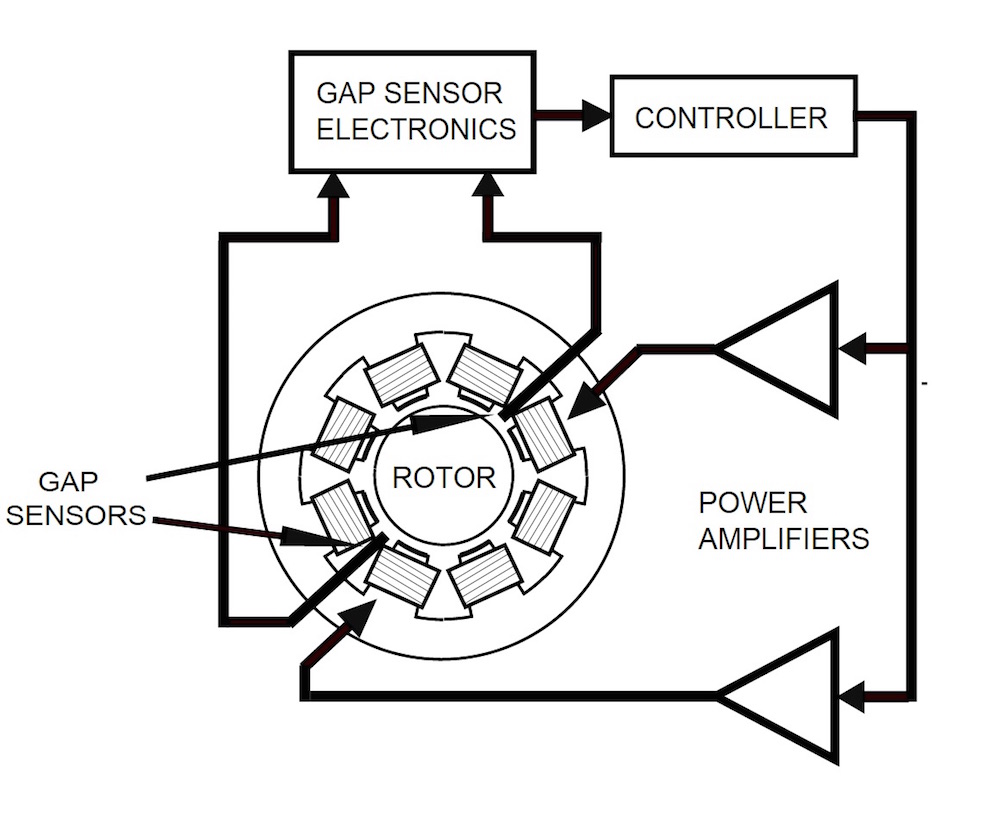
有源磁轴承组件的示意图。图片属于公有领域，通过 Wikimedia Commons 共享。

有源磁轴承的优点是能主动控制转子的位置，但与此同时，这也造成电子电路功耗较大，运行成本较高。当然，我们可以通过优化电磁体的设计，降低运行所需的功率，从而减少运行成本。COMSOL Multiphysics 便是这一优化过程中可以使用的有用工具。

在模拟包括定子和转子在内的有源磁轴承时，最佳途径是使用“AC/DC 模块”中的旋转机械，磁 接口。这个模拟过程与发电机或电动机的模拟非常相似，请查阅我们的二维发电机教程。要获取通用指南，请参考上一篇博客如何模拟三维旋转机械。

使用磁场 接口可以模拟永磁体和导电线圈（单匝或多匝线圈）。但是由于存在旋转，所以无法模拟感应电流。如果感应电流可以忽略不计，那么模型就可以建立在稳态域或频域，并对转子的各个位置添加参数化扫描研究，从而计算磁力或扭矩。

无源磁轴承

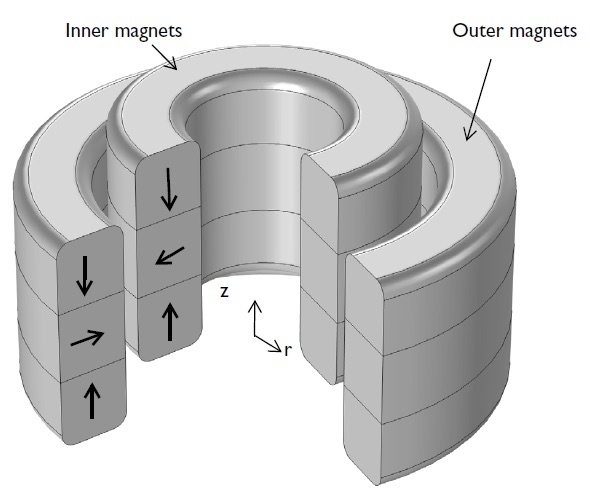
无源磁轴承 使用永磁体，不需要传感器和控制电路或输入功率。永磁体上两个磁极之间的磁斥力使空气间隙的长度保持不变，如永久磁轴承所示，或者依靠永磁体与旋转导电盘或轴之间的电动悬浮（EDS）也可以使这个长度保持不变，如电动轴承所示。 使用永磁体的无源磁轴承的几何与仿真结果显示如下。

左图：使用永磁体的轴向磁悬浮轴承的几何。黑色箭头表示永磁体的磁化方向。右图：显示磁通密度（箭头图）的结果图以及磁通密度模的曲面图。

电动轴承

当导电的转子在永磁体产生的磁场中旋转时，这个转子上会感应出涡流。这些涡流反过来会形成一个与永磁体产生的磁场方向相反的磁场，从而在旋转的转子导体与静态永磁体之间产生排斥力。转子的位移一直在这一磁斥力的作用下保持不变。因此，转子在中心旋转时，间隙的长度不变。

电动轴承可进一步分为径向电动轴承和轴向电动轴承。磁通量与转子轴平行时为径向电动轴承，磁通量与转子轴垂直时为轴向电动轴承。

径向电动轴承

径向电动轴承 由一个固定在旋转轴上的导电圆柱体构成。永磁体零件堆叠在铁环之间，定子和转子间的空气间隙中会产生沿半径方向（与轴线垂直）的朝内或朝外的磁通量。电动轴承教程是使用磁场和电场 接口求解的，可从“案例下载”中下载。还计算了不同偏移位置上的磁力。

左图：径向电动轴承的三维几何。右图：显示有定子（铁芯和磁体）的磁通密度（x 轴偏移位置为 1.5 毫米时）以及导电转子中涡流（灰度标）的径向电动轴承。

轴向电动轴承

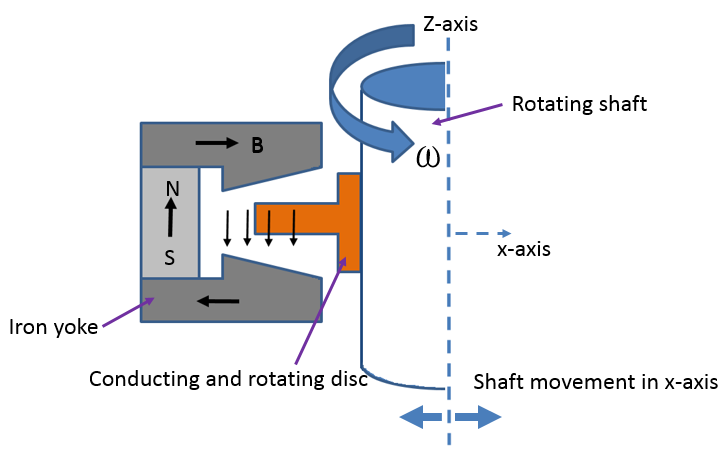
轴向电动轴承的截面剖视图配置如下所示。导电盘贴着转子，磁性材料（轭铁）用于引导永磁体的磁场，从而使磁通线平行于转子轴。这就是术语轴向电动轴承 的由来。

在这个设计中，空气间隙相对较小，磁通路径十分高效。相关的完整教程可以从“案例下载”中下载。

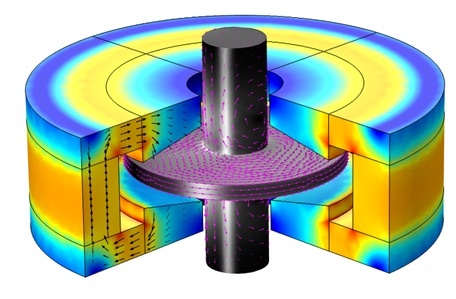
左图：轴向电动轴承的截面剖视图。右图：显示有定子磁通密度和导电转子涡流的轴向电动轴承。还显示了箭头图。

上述两个电动轴承示例在 COMSOL Multiphysics 中都是用磁场和电场 接口模拟的。在这两个示例中，速度（洛伦兹项） 特征都用于指定旋转速度。使用这个方法后，就无需利用移动网格 接口考虑转子的旋转了。

请注意，只有当移动域不包含随材料一起移动的指定磁源，如线圈或永磁体（固定或感应的）时，才可以使用“速度（洛伦兹项）”特征。移动域的运动方向必须保持不变。比如，“速度（洛伦兹项）”特征可以用于模拟导电的（非磁性的）均匀旋转盘。相关的例子有电磁制动器、电动轴承、单极发电机、无限均匀移动平面上的磁体（如磁铁在铜管中下落或磁悬浮列车）以及流经磁体的均匀导电流体的流动（如液态金属泵或霍尔发生器/霍尔推进器）。

注：洛伦兹项准确地描述了移动域中由稳态磁源引起的感应现象，前提是移动域（包括其材料属性）不会随运动方向而变化。此外，感应现象可能是由于稳态源的强度或不断改变的速度的短暂变化引起的。洛伦兹项不会考虑到此类短暂变化带来的影响。

磁力/扭矩

COMSOL Multiphysics 中有两种方法可用于计算电磁力和扭矩。最常见的方法是 Maxwell 应力张量 法，常用于以下接口中的计算力 特征：磁场 接口；磁场，无电流 接口；磁场和电场 接口；以及旋转机械，磁接口。

举例来说，添加了计算力 特征后，就可以在磁场接口中使用磁力的空间分量 (mf.Forcex_0, mf.Forcey_0, mf.Forcez_0) 和轴向扭矩 ( mf.Tax_0) 进行后处理。计算力 特征只对 Maxwell 应力进行积分，仅计算选定的一个域（或多个域）外侧以及可选择域的整个外部边界上的应力，这几个域应当是一起移动的一组域（一个机械体）。因为这种方法基于表面积分，所以计算的力易受网格大小的影响。使用这种方法时，往往需要执行网格细化研究，才能使计算得到的力或扭矩正确。

如果应用了“计算力”特征的域与外部边界、周期性边界和一致对相接触，则“计算力”得到的结果可能不正确。而且，要计算附加在铁磁表面的磁体的力，接触边界上必须指派一个薄低磁导率间隙（在静电边界则指派薄低介电常数间隙），因为要计算的是空气中的 Maxwell 应力，而不是铁磁（电介质）材料中的 Maxwell 应力。

第二种方法是洛伦兹力法，仅适用于计算非磁性导电域中的磁力这种特殊情况。洛伦兹力定义为 F = J × B，其中 J 表示电流密度，B 表示磁通密度。洛伦兹力能十分准确地计算导电域中的力，因为其计算依据的是体积而非边界。因此，尽可能优先使用洛伦兹力法，而非 Maxwell 应力张量法。

除了以上提到的内置方法之外，还可以使用虚功法或虚位移原理计算磁力和扭矩。在这一技巧中，力的计算也就是研究少量位移对电磁能的影响。在 COMSOL Multiphysics 中通过使用针对变形网格和灵敏度分析的特征，可以实现虚功法。

磁刚度

在固体力学中，刚度表示一个物体的硬度，即物体在受力时抵抗变形的程度。在磁悬浮轴承应用中，这个参数相应地定义为磁刚度，它是总磁力相对于位置的负导数。如果磁力为 F_z，那么磁刚度相对于位置 z 的计算公式为：

链接教程阐述了如何利用该方法计算轴向磁悬浮轴承的磁刚度。不过这个示例仅适用于二维轴对称的轴承，因此无法得到 x 向和 y 向的磁刚度。要计算所有方向上的磁刚度，需要在三维中模拟此问题。下面，我们将对上述轴向磁悬浮轴承创建一个三维模型，并确定其刚度 k_x 。可以从“案例下载”中下载这个示例教程。

这个方法主要涉及使用磁场，变形几何 接口以及灵敏度 接口。同二维模型一样，我们也会用到磁场 接口。磁体模拟时使用了安培定律 特征，其本构关系设置为 1[T] 的剩余磁通密度。计算力 只须添加到内部磁体，并将几何参数化，使内部磁体的位置在 x 方向上存在 X0 的偏移。参数 X0 随后会用于参数化扫描。另外，变形几何 接口将用于分析向 x 方向的附加（虚拟）网格位移 dX 所施加的力的灵敏度。计算 x 向的磁刚度时这里仅使用四分之一几何。

注意，此配置中仅正确计算了 x 轴上的力。根据对称性，y 向和 z 向的力应当为零。不过因为仅模拟了四分之一几何，所以计算出的力会相当大。同样地，还可以计算 y 向的刚度，即根据 yz 平面和 xy 平面分别对称地切割整个模型，获得四分之一模型并对其进行分析。

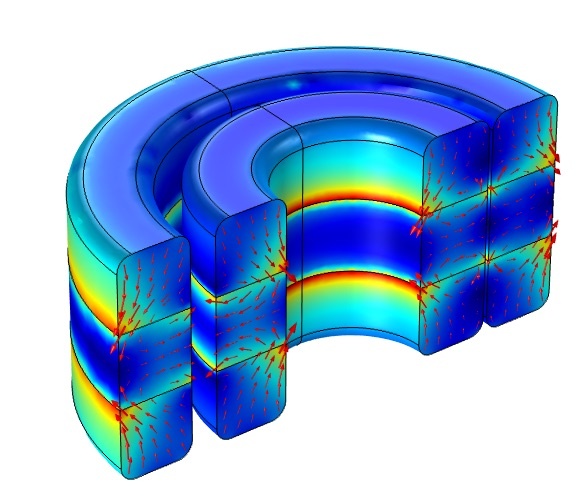
左图：用于计算刚度的轴向磁悬浮轴承的四分之一三维模型。右图：半个模型中的磁通密度模和磁通密度箭头图。结果是使用“三维镜像”数据集在 xy 平面绘制的。

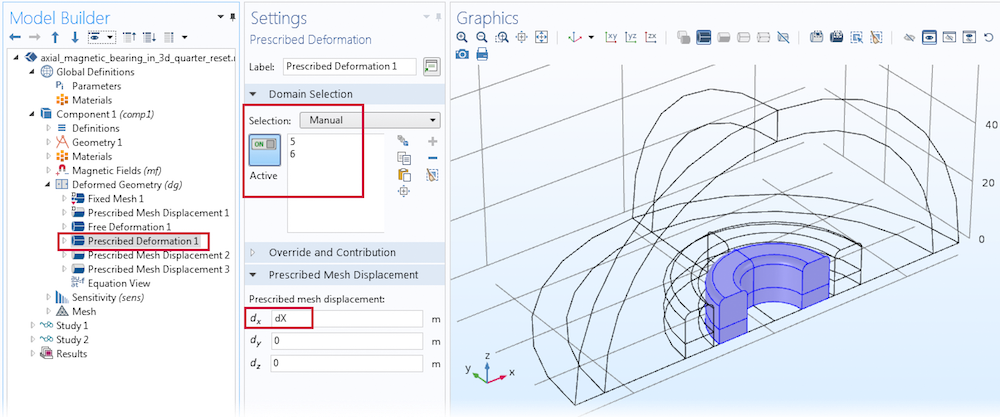
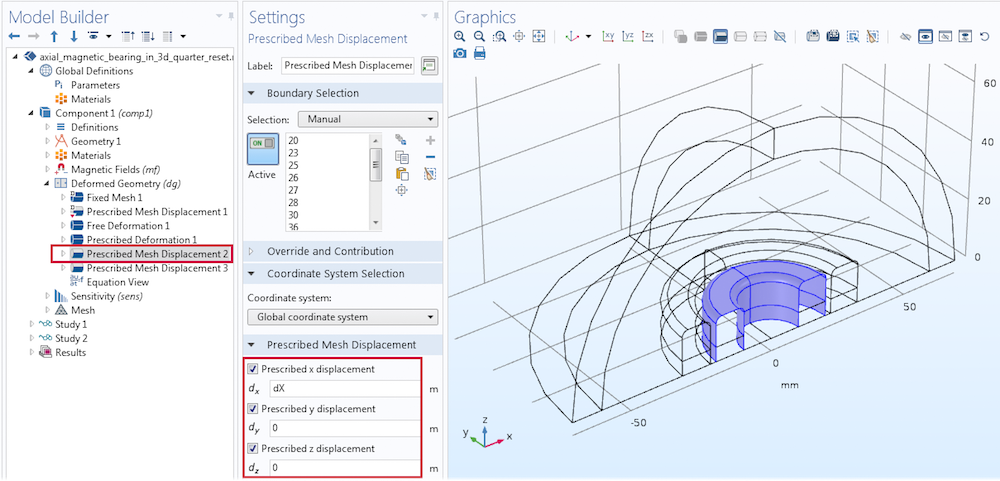
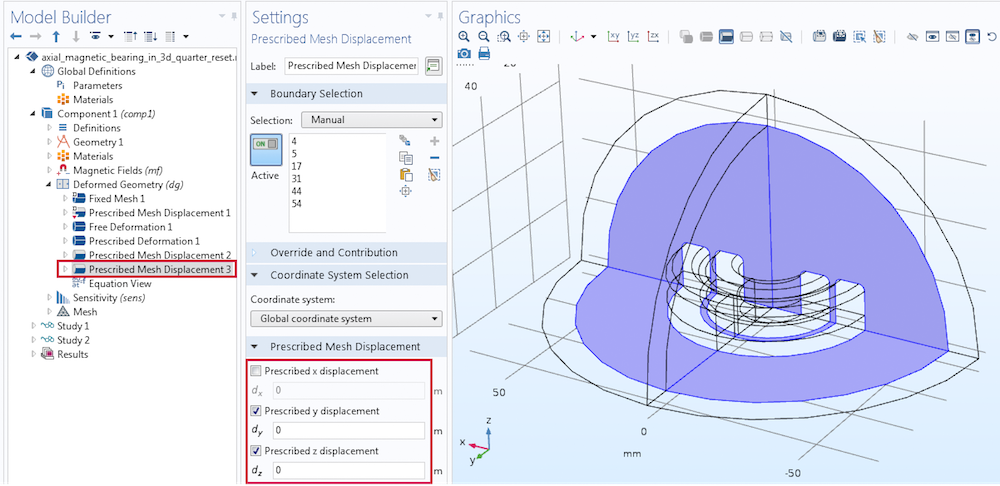
变形几何 接口对无限元域以外的所有其他域都进行了求解。要求解这个区域，首先在磁体附近的空气域添加一个自由变形 节点。同样地，可以向沿 x 轴的内部磁体域添加一个指定的变形 dX。最后，向内部磁体边界和对称的截平面边界添加两个指定网格位移 节点，如下图所示。

内部磁体域上设置的指定变形。

内部磁体边界上设置的指定网格位移。

对称截平面上设置的指定网格位移。

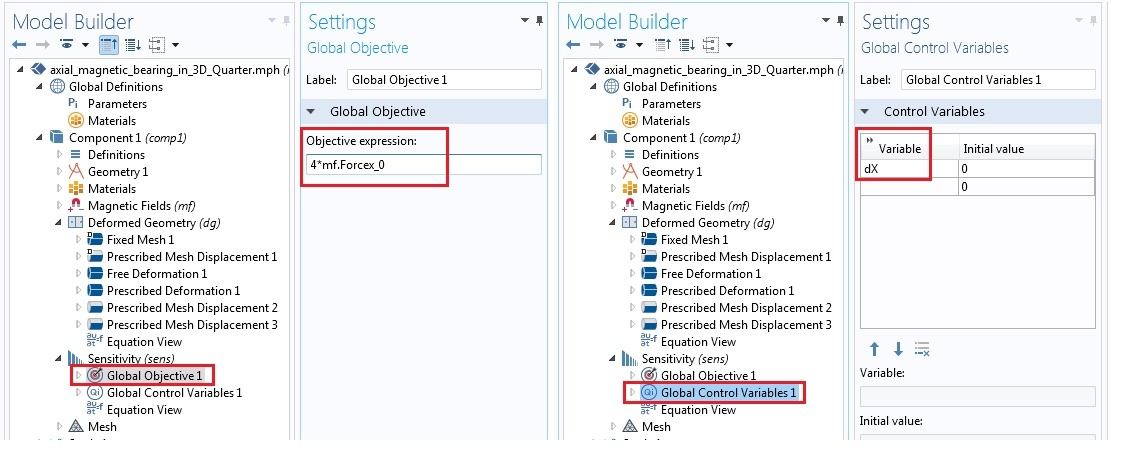
在灵敏度 接口中添加全局目标 特征，在“全局目标”设定下的目标表达式中指定 x 向的总力（即，4*mf.Forcex_0）。这里，mf.Forcex_0 指磁场 接口中“计算力”特征计算出的 Maxwell 应力张量力的 x 分量。同样地，添加全局控制变量 dX，如下图所示。

全局目标设置（左图）和全局控制变量设置（右图）。

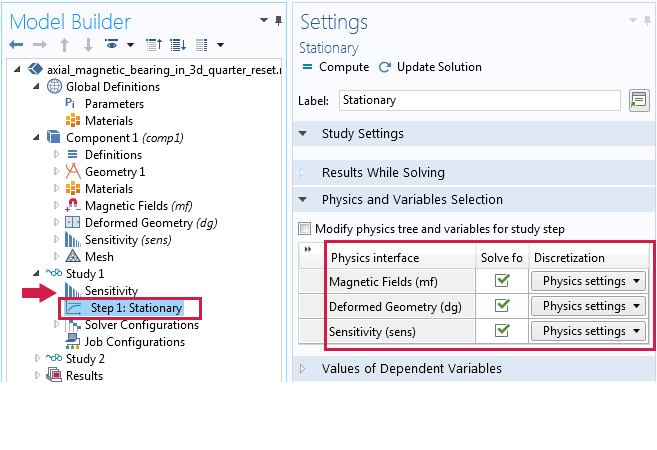
因为灵敏度（和优化）研究不能与参数化扫描 研究节点合并，所以模型必须在两个单独的研究中求解。第一个研究包含灵敏度求解器和稳态求解器。随后的第二个研究包含参数化扫描研究，但会使用研究 1 作为参考。对参数 X0 在 range(0,1.5/20,1.5) 区间内执行参数化扫描，其设置如下。

左图：灵敏度分析的稳态研究设置。右图：以研究 1 为参考的参数化扫描研究设置。

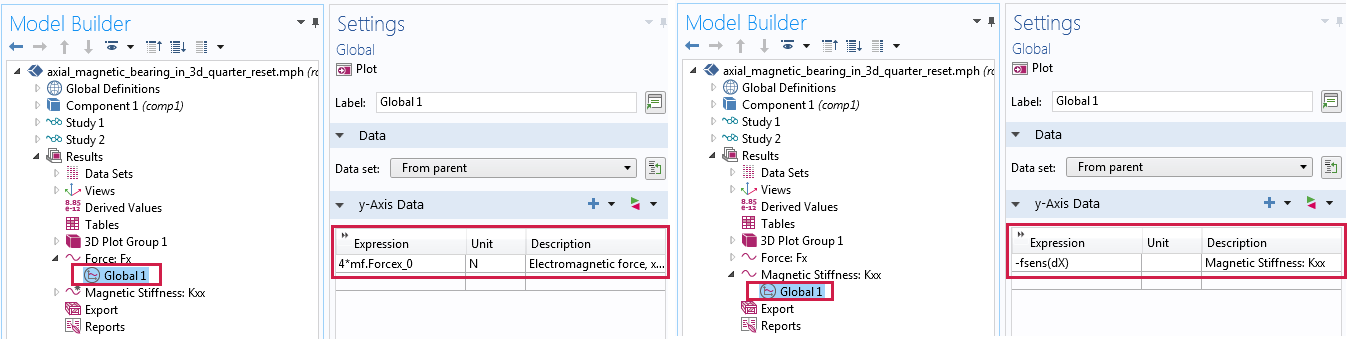
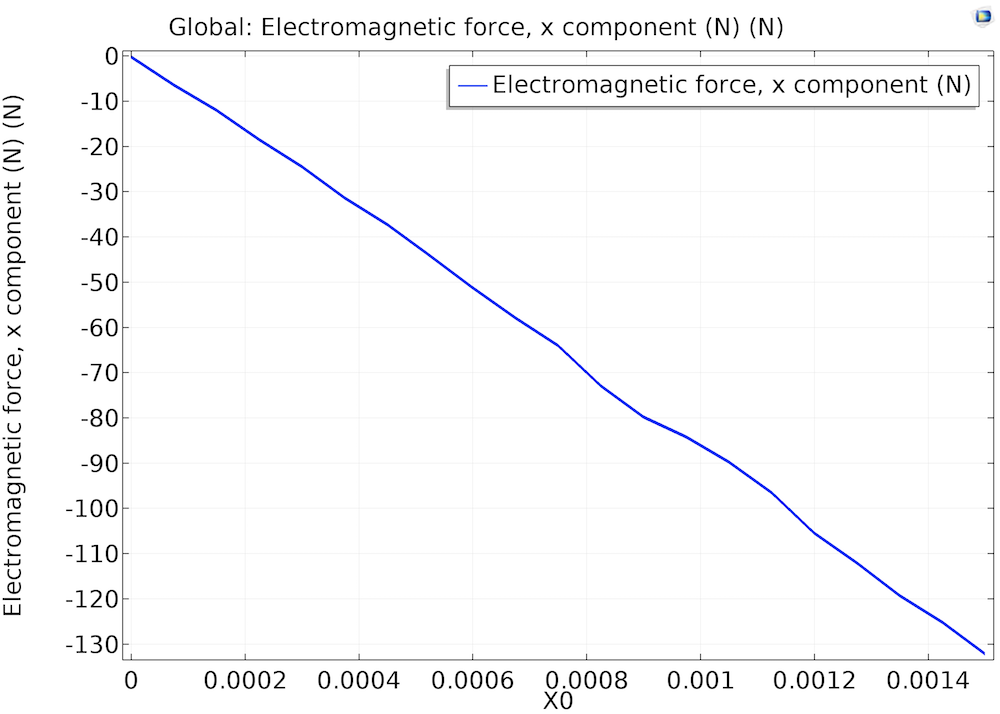
将 x 轴上的磁力和 x 向的磁刚度绘制为一维全局图。

磁力图的设置（左图）和磁刚度的设置（右图）。

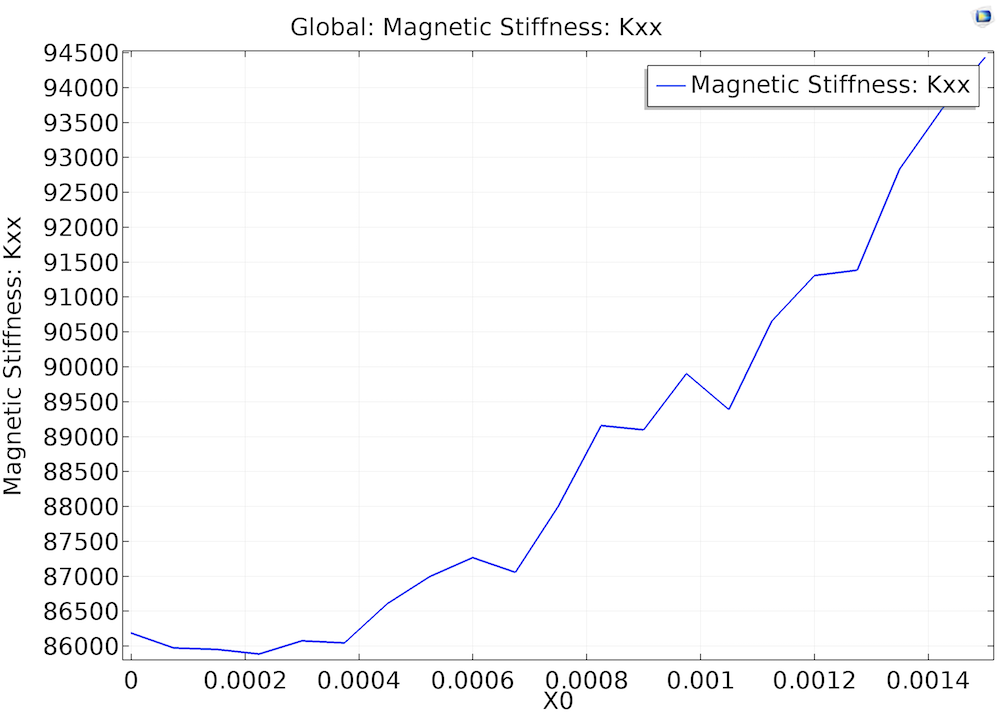
左图：电磁力的 x 分量是 x 轴上偏移的函数。右图：磁刚度 k_xx 是 x 轴上偏移的函数。

总结

在本文中，我们讨论了使用 COMSOL Multiphysics 的 “AC/DC 模块”的接口可以模拟的几类磁悬浮轴承。仿真简化了这几类轴承设计参数的计算方法，从而优化了轴承性能，延长了使用寿命。

在这一系列的下一篇博客中，我们将重点讨论如何使用 COMSOL Multiphysics 模拟磁齿轮。敬请关注！

编者注：本篇博客文章于 2017 年 9 月 5 日更新。