
当一滴水附着在金属表面时,一般是腐蚀的开始。在某些情况下,如果有足够的接触时间,这种腐蚀可能会导致金属表面形成一个非常小的腐蚀坑。在这种条件下,腐蚀坑会逐渐发展,最终导致腐蚀坑底部成为阳极,腐蚀坑周围成为阴极,这样就会加速腐蚀坑底部的腐蚀,并可能形成一个大凹坑。模拟点蚀的目的是了解在特定条件下哪种材料或设计更容易发生点蚀。本篇博客文章讨论了研究点蚀模型可能是什么样的。
腐蚀过程简介
电偶腐蚀是由对电子具有不同亲和力的两种金属的电子和离子接触引发的。如果将两种这样的金属与同一种电解质接触,会在固液界面形成双电层。这两种金属在双电层上的电压是不同的。这导致电子从较不贵重(注:化学性质较活泼)的金属传导到较贵重的金属,如图 1 所示。
在贵金属表面,这些电子可能参与电荷转移反应,其中在贵金属上发生净还原反应(阴极反应);在较不贵的金属上,电子被带走,并且这种电荷转移反应可能导致较不贵的金属在净阳极反应中溶解。
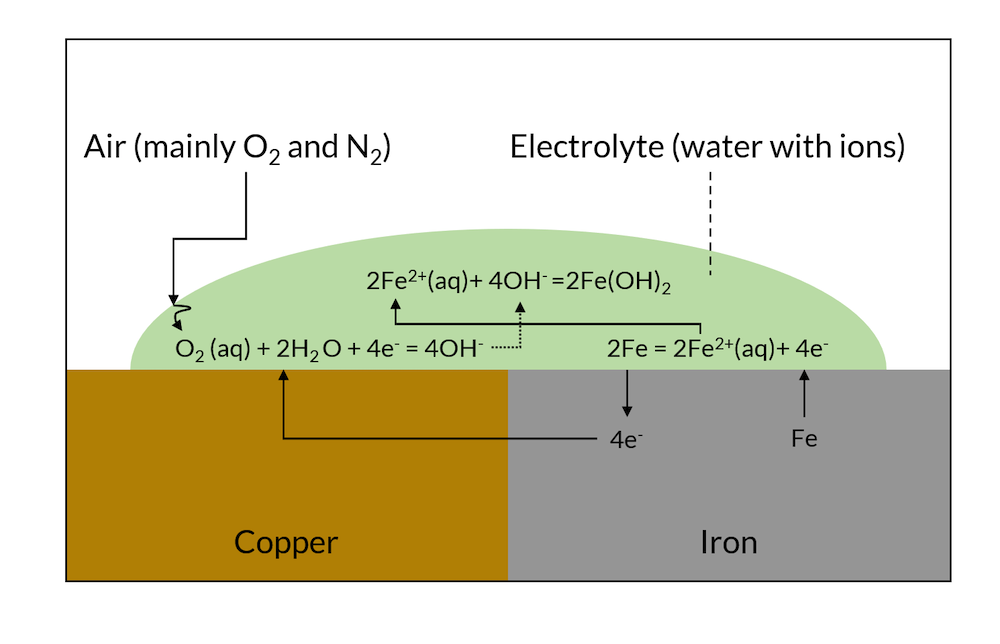
图1 电偶腐蚀示意图。
当图 1 中的反应进行一段时间后,较不贵重的金属(在这种情况下是铁)可能已经在较贵重金属的接触面附近溶解,如下图2所示。
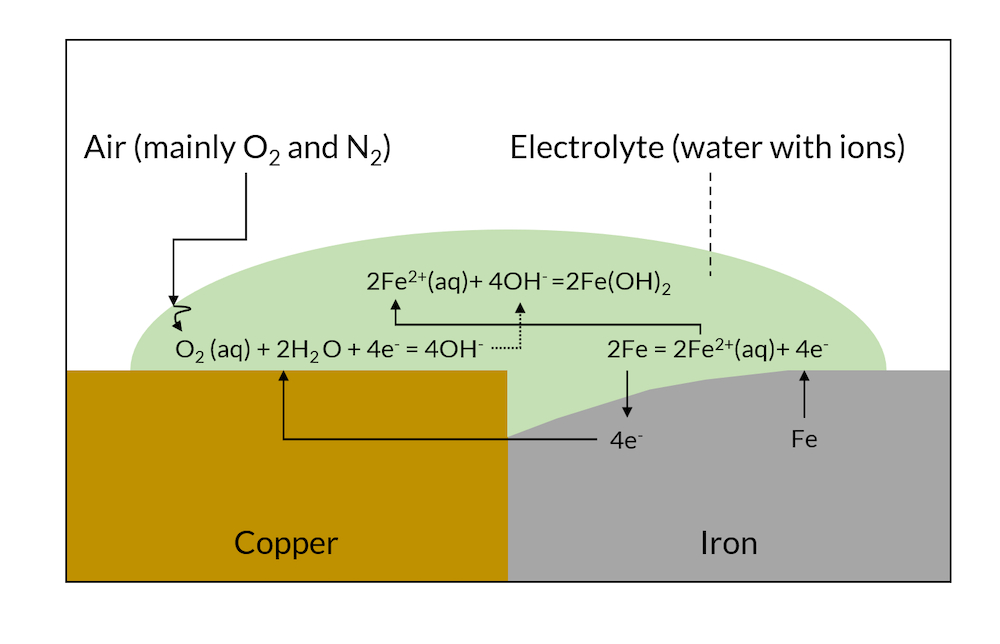
图2. 一段时间后,电偶腐蚀可能溶解了靠近铜接触区域的部分铁金属。
现在我们可以观察单个金属表面的一滴水,见图3。微观结构可能具有不同金相,这些区域的电子亲和力可能略有不同。这意味着,例如,阴极反应可能发生在金属微晶区域,而阳极反应可能发生在晶间区域。
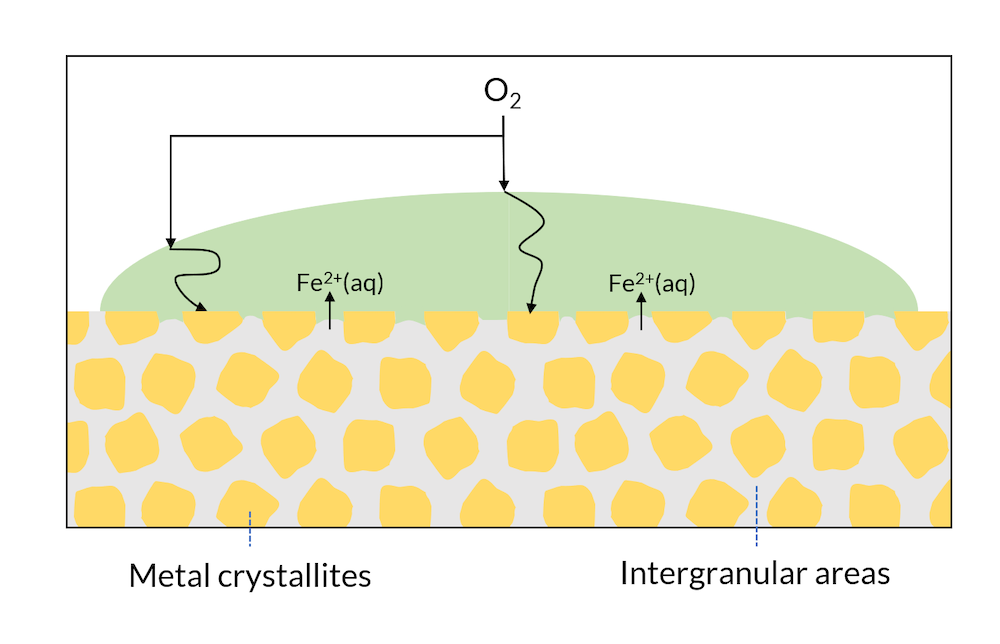
图3. 金属表面的区域可能由晶体和晶间区组成。
在图2 中,可能会在铁离子释放的表面附近形成氢氧化铁。这是铁生锈的一部分原因。在图3 中,由于晶间区分布均匀,所以整个表面都可能会生锈。这通常被称为全面腐蚀。
现在我们来看看图4,假设图3 中的反应正在继续。相比与氧扩散长度较小的边缘,氧在液滴中间向微晶表面的传输距离更长。液滴中间金属表面的氧气已耗尽,这使得该区域的电位相较于液滴边缘的区域有所降低。当电位被降低到铁的钝化电位以下,就可能会使氧化铁的保护层不稳定。最终,由于缺氧,表面中间的微晶可能充当净阳极。这导致液滴中间的铁溶解逐渐形成腐蚀坑。产生的铁离子还会与水发生反应,形成质子,从而降低坑内的 pH 值。pH 值降低会导致更快的腐蚀速率。这个过程在被第一次解释和重现之后被称为Evans drop实验(参考文献1)。
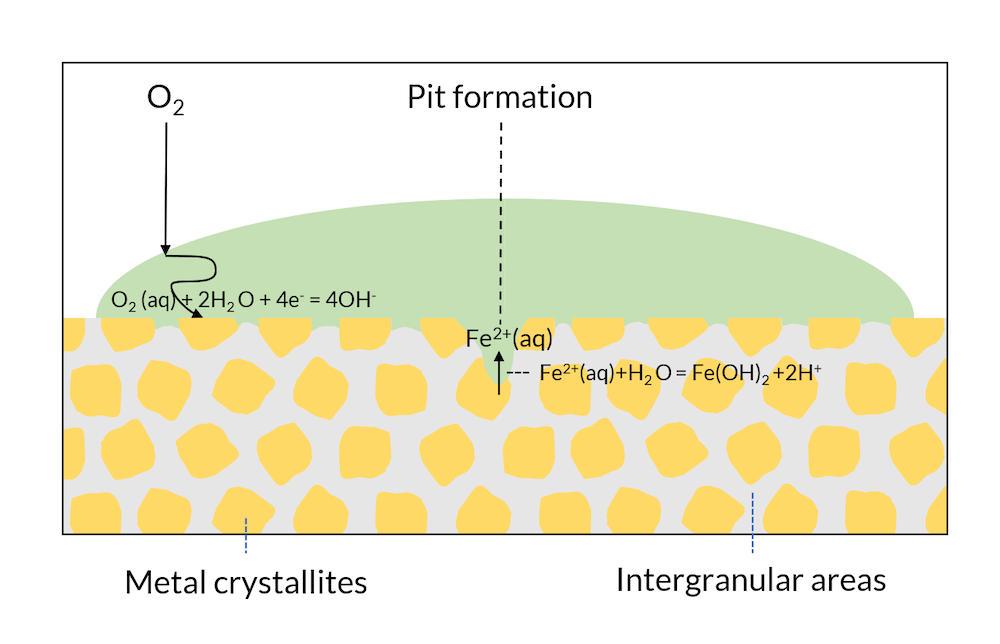
图4. Evans drop 实验。腐蚀坑坑的形成还会导致凹坑中的 pH 值降低,从而进一步加速阳极反应。
腐蚀坑的诱发也可以通过其他机制发生。例如,金属表面的机械压痕或杂质可能会削弱局部铁表面氧化层的保护作用。尤其是不锈钢表面具有一层保护性氧化层,可能会受到机械或化学损坏。
模拟点蚀
本文中模拟的模型从已经形成的腐蚀坑开始。我们还假设在建模域之外有一个非常大的区域,这提供了一个稳定的混合电势,在更大程度上不受局部电流的影响。同时提供了远离腐蚀坑的恒定电解质电势。
建模过程中所考虑的反应是:
- 铁在阳极极化表面溶解:\[2Fe = 2F{e^{2 + }}\left( {aq} \right) + 4{e^ – }\]
- 电解液中的沉积反应:\[F{e^{2 + }}\left( {aq} \right) + 2O{H^ – } = Fe{\left( {OH} \right)_2}\left( s \right)\]
- 电解液中水的电离:\[{H_2}O = {H^ + } + O{H^ – }\]
模拟的化学物质如下:
- \[F{e^{2 + }}\]
- \[{H^ + }\]
- \[O{H^ – }\]
- \[N{a^ + }\]
- \[C{l^ – }\]
假设水的电离处于平衡状态,可以消除氢氧根离子的浓度。其他离子,在这种情况下是质子,可以用电中性条件消除。在 COMSOL Multiphysics® 软件中可以通过在 三次电流分布,Nernst-Planck 接口选择水基电中性 选项自动处理这两种消除。请注意,所有离子的传输方程都包含在电解质电流密度表达式中的电流守恒。最后一个因变量是电解质电位。
对于初始状态,我们假设沉积反应在凹坑内部产生了沉积物,因此可以将凹坑视为多孔结构,其中电解质填充在孔隙中。这是一个合理的假设,因为沉积物很可能是由曾经位于腐蚀坑所在位置的金属形成的。此外,我们还假设模型域为轴对称,如图5 所示。
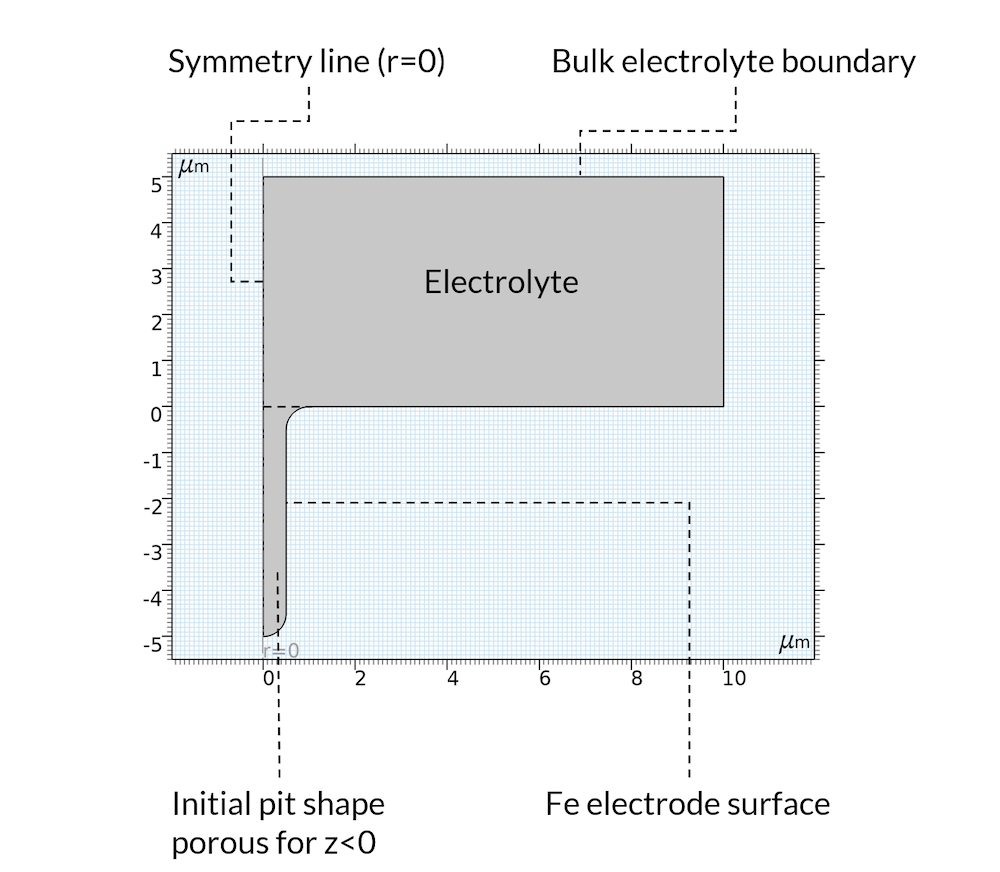
图5. 模型域的几何形状和边界。
金属溶解反应被定义在上图5 中所示的“Fe 电极表面”边界。假定阳极反应速率与质子浓度成正比。这适用于存在氯化物的酸性条件(参考文献2)。使用移动网格将铁溶解反应与边界位移耦合。
如上所述,我们没有模拟氧还原反应。相反,我们在远离凹坑的水平位置设置了一个恒定的电解质电位,我们称之为“整体电解质边界”。在此边界处,我们还设置了钠离子、氯离子和铁离子浓度。
在电解质领域,包括腐蚀坑,我们假设水的电离和氢氧化铁反应都发生。请注意,由于氢氧根在 Fe(OH)2(s) 的产生中被消耗,这也会导致 pH 值降低,这在前面的图4 中已经提到。
物质的初始浓度和初始电解质电位是通过求解初始几何形状来计算的,假设该过程处于准稳态。这意味着,对于一个固定几何图形,使用稳态求解器在上述边界条件下求解。这个结果是在 t=0 时物质的成分分布和电解质电位分布。该解是瞬态研究的初始条件。
结果
初始准稳态似乎是一个合理的假设,因为电解质成分和电位的变化在开始时相对较慢,约 0 ~1 天。
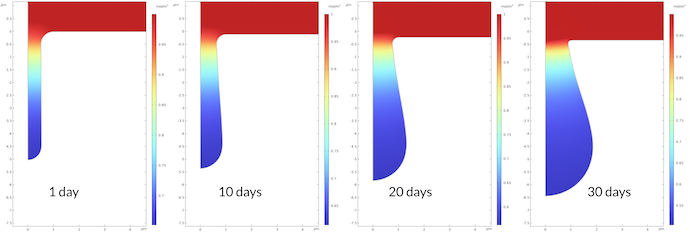
下图 6 显示了腐蚀坑在 30 天内的增长情况。凹坑内电解液电位梯度大。腐蚀坑内的电解质电位在 0.43mV 和 16.5mv 之间变化,而在 30 天后,腐蚀坑外的电势从 0mV 变化到 0.43mV。请注意,坑中的传质较慢,,我们假设与外部电解质相比多孔介质的有效传输效率较低。在整个模型计算时段内观察到相同的定性电位分布,观察到腐蚀坑的底部比坑口生长得更快。这导致坑口处电流的路径相对较窄,从而导致坑口中电解质电位的梯度更大。请注意,我们确实在平坦表面上受到了一些腐蚀。30 天之后,表面的位移约为 0.35 微米,而同样的坑底位移为 1.45μm。
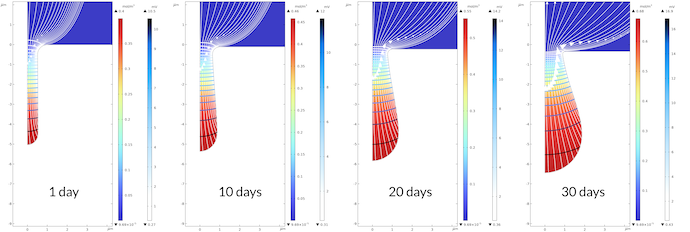
图6. 坑底比坑口长得快。这导致靠近坑口的电解质电位梯度更大。
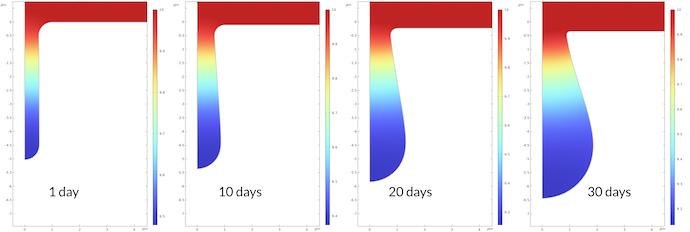
图7 显示了腐蚀过程中 pH 值的变化。1 天后坑底 pH 值为 9.48,30 天后为 9.14。这可能看起来不是一个很大的变化,但它对应的 30 天后质子浓度比 1 天后高 2.2 倍。腐蚀过程的速率常数与质子浓度成正比,这也意味着腐蚀速率相应加快。
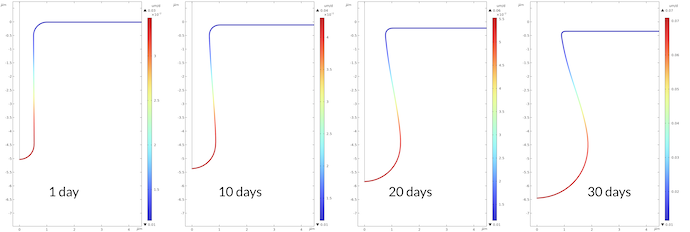
图8 显示的腐蚀速率是以四倍 μm/天绘制的。坑底部的最大腐蚀速率在 30 天后比 1天后的腐蚀速率高 2.3。这与质子浓度在 30 天后比 1 天高 2.2 一致。
钠离子的浓度分布与铁离子的分布相反。原因是电中性条件。当铁离子被推入电解质时,钠离子被推出坑外。与钠离子相反,氯离子被推入坑中以保持电中性(未显示)。
这个模型清楚地显示了点蚀的“恶性循环”特点。这个过程随着时间的推移而加速,直到凹坑足够深,从而使欧姆损失和腐蚀产物成为限制。
结束语
这个模型的一个简单可能的扩展是考虑沉淀腐蚀产物的物料平衡。这些产物的密度比铁金属低,因此会在腐蚀凹坑中形成,但也会被推到凹坑外。这可以通过引入孔隙率将其作为因变量建模,其中氧化物的传输可以用层流描述。
这个模型的另一个自然扩展是考虑完整的液滴几何形状,以包括氧扩散和氧还原。
这个模型的第三个扩展将包括更详细的化学过程,例如,通过包括更多的铁离子、更多可能的氧化还原反应以及金属表面的更多铁氧化物和氢氧化物。当然,我们也可以使用现有的模型,尽管建模过程相对简单,但它非常先进。
下一步
参考文献
1. U.R. Evans, “Corrosion and Oxidation of Metals”, Amolds, p. 118., 1960.
2. H.C. Kuo and K. Nobe, “Electrodissolution Kinetics of Iron in Chloride Solutions”, J. of Electrochem. Soc, vol. 125, no.6, 1978.





评论 (9)
Yuchen XI
2022-10-31请问该仿真有案例吗
Ed Fontes
2022-10-31 COMSOL 员工Dear Yuchen Xi,
You can download the files here:
https://www.comsol.com/model/pitting-corrosion-100101
Best regards,
Ed
Yuchen XI
2022-10-31找到了 谢谢
利刚 张
2022-11-10参考文献1和2在哪可以找到
Ed Fontes
2022-11-10 COMSOL 员工References
1. U.R. Evans, “Corrosion and Oxidation of Metals”, Amolds, p. 118., 1960.
2. H.C. Kuo and K. Nobe, “Electrodissolution Kinetics of Iron in Chloride Solutions”, J. of Electrochem. Soc, vol. 125, no.6, 1978.
Best regards,
Ed
利刚 张
2022-11-19谢谢
雨辰 辛
2024-06-19Dear Dr. Ed Fontes,
I have several questions regarding electrochemistry.
Why is it possible to accurately simulate the pitting corrosion of iron without modeling the oxygen reduction reaction?
What is the effect of setting a constant electrolyte potential at positions far from the pit?
Can I describe the oxygen reduction reaction, which occurs as a cathodic reaction on the iron surface, without setting a constant electrolyte potential, by using electrode kinetics equations instead?
I look forward to your answer, thank you!
yongchao wang
2024-06-21 COMSOL 员工1.模型中在远离腐蚀坑的边界上设置了“电解质电位”表示阴极反应的贡献,这个贡献可以是氧气还原反应的贡献,也可以是其它阴极反应(如:金属阴极或外加电流)的贡献;
2.可以在不设置“电解质电位”边界条件时,添加电极Fe表面氧的还原反应,实现大气环境中点蚀坑发展的仿真,可参考案例:https://cn.comsol.com/model/corrosion-under-an-evans-droplet-113981
Miles Hsin
2024-06-21感谢您的耐心回答,对我很有帮助!