
当提起珠串时,你会想到什么?也许是在美国路易斯安那州新奥尔良市狂欢节庆祝活动期间的繁忙街道,或是在夏令营中制作友谊手链。或者,如果你对研究聚合物感兴趣,你可能会想到:当对黏弹性流体施加一定的力时,流体如何开始看起来像绳子上的珠子。今天这篇博客,让我们来看一个使用 Oldroyd-B 聚合物的例子。
黏弹性流体
顾名思义,黏弹性流体是具有弹性的流体。当黏弹性流体变形时,一定的力试图使其恢复到未变形的状态。这类流体包括:
- 聚合物熔体
- 油漆
- 蛋白质悬浮液

油漆是一种黏弹性流体。
2020 年,聚合物流动模块随着 COMSOL Multiphysics® 软件 5.6 版本一起发布,包括黏弹性流体模型。我们可以使用这些模型来解释流体的弹性并预测其施加的力、涂层的均匀性和模具填充程度。
聚合物流动模块中包含以下黏弹性流体模型:
- Oldroyd-B 流体
- Gisekus
- FENE-P
- LPTT
这里,我们将重点介绍 Oldroyd-B 流体的长丝由于表面张力效应而拉伸时的模拟结果。如果你想逐步构建这个模型,请随时点击此处下载:“黏弹性细丝的串珠结构”案例模型。
模拟 Oldroyd-B 聚合物中的表面张力效应
我们的示例模型是从建立一条长的、未拉伸的 Oldroyd-B 流体细丝开始的。细丝被建模为一个初始半径有小幅扰动的液体圆柱体,流动被建模为轴对称。
Oldroyd-B 流体被建模为聚合物在牛顿液体中的稀溶液。聚合物本身由两个物理参数来表征:
- 黏度
- 弛豫时间
由于这个问题是无量纲的,为了模拟黏弹性细丝变细时的动力学,我们使用了两个无量纲参数:
- Deborah 数(无量纲聚合物溶液弛豫时间)
- Ohnesorge 数(惯性-毛细和黏性-毛细时间尺度之比)
模拟结果
我们可以确定黏弹性丝在不同时间步长的演变,如下图所示,这与文献中现有的实验和模拟结果非常吻合(参见教程模型文档中的参考文献 1)。

长丝在 0、20、30、100 和 300 s (从左到右)时的轮廓。
仿真结果还显示了作为时间函数的最小长丝半径。由此我们可以知道,在长丝迅速形成串珠结构后,有一个缓慢变细的过程。这种变细的速度可以通过表面张力效应和弹性力的平衡来确定。
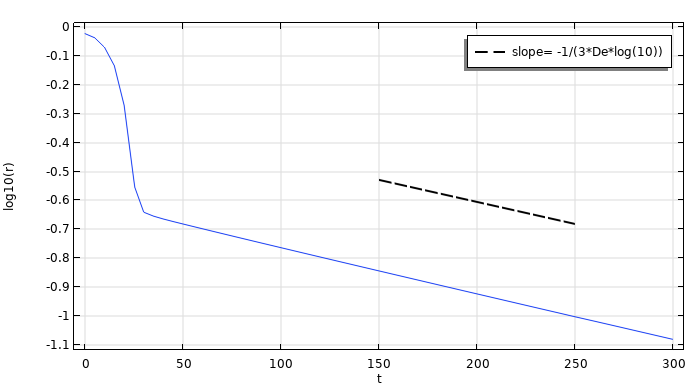
作为时间的函数的长丝最小半径。
当时间远大于弛豫时间时,黏弹性丝由几乎呈球形的液滴组成,这些液滴由指数级变细的线连接。

我们还可以看到,当黏度特别低或表面张力特别高时,会在串珠结构中形成卫星液滴(需要使用更细的网格运行模型才能看到它们)。
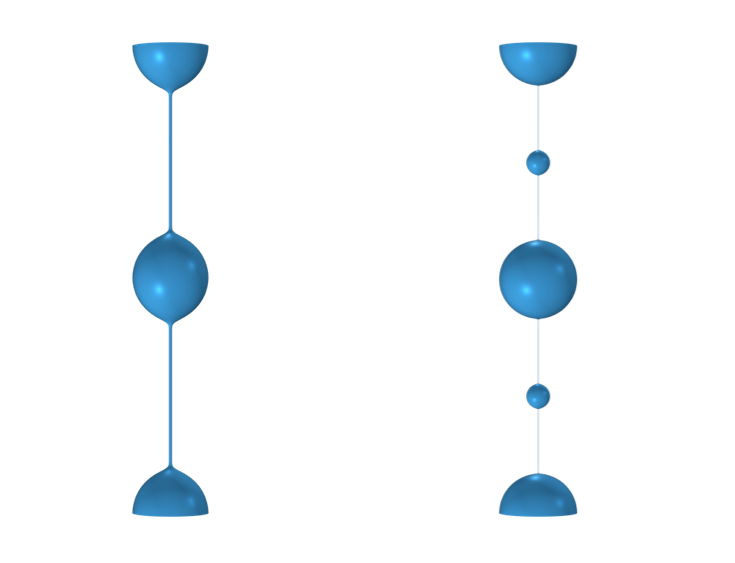
没有卫星液滴(右)和有卫星液滴(左)的黏弹性流体细丝。
自己尝试
文中我们省略了模拟过程直接跳到了结果,您可以在 COMSOL 案例库中下载文档和 MPH 文件,详细了解如何构建黏弹性细丝的串珠结构模型。



评论 (0)