模拟半透明材料的脉冲激光加热

使用聚焦激光快速加热材料常被用在在各种应用中，包括半导体加工行业。这篇博客，我们将研究具有周期性脉冲强度的高斯轮廓激光束，来加热沉积在硅衬底上的两种不同的半透明材料。为了建立此模型，我们将使用温度场和比尔-朗伯定律求解一个多物理场建模问题。接下来，让我们进一步探讨这个模型，看看如何设置它。

高斯轮廓激光束照亮硅晶圆

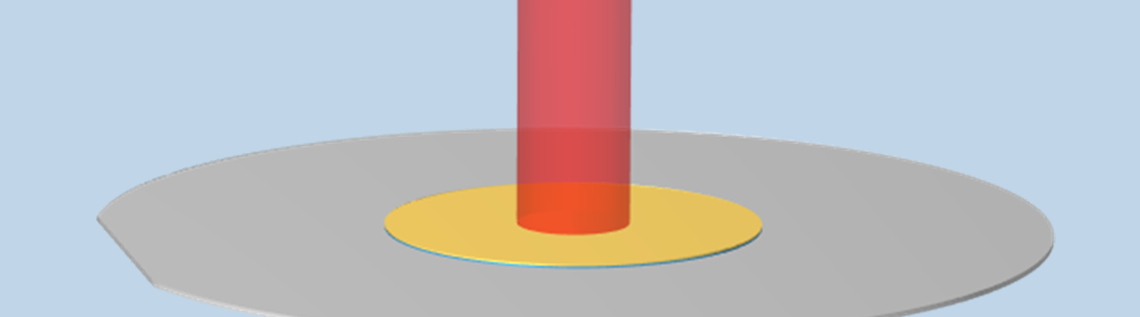
我们将以一个直径为 2 英寸（约 5cm）的硅晶圆为例，如下图所示，该晶圆的中心有两种不同的材料，每种材料厚度为 100μm，半径为 1cm。晶圆从顶部被一束高斯轮廓激光热源照射，该热源在时间上被快速脉冲化。这两种材料在 700nm 的激光波长下都是半透明的，但在更长波长的红外辐射下是不透明的。硅衬底是掺杂的并且在所有波长下都是高吸收性的。

脉冲激光在不透明晶圆上照亮了两层半透明材料。

由于所有材料都具有与入射光束垂直的平面边界，所有入射光都将沿平行于入射光束的均匀方向传播。材料之间的界面会有反射，但没有折射或衍射。两层材料的厚度都远大于波长，因此我们可以假设相干长度远小于层厚度。我们可以使用比尔-朗伯定律来解决这个问题，该定律描述了半透明介质中光的衰减。该方程使用 COMSOL Multiphysics^® 软件中的吸收介质中的辐射束 接口求解。但是，由于存在反射，我们需要仔细研究一些细微差别。

了解物理场并设置模型

由于沉积层是圆形的，并且由于激光聚焦在中心上，我们可以忽略晶圆平面并将模型视为完全轴对称的。这使我们能够将模型简化为 2D 轴对称建模平面。在这个平面中，我们简单地绘制三个矩形来定义晶圆和两个沉积层，并为这三个矩形分配不同的材料属性。这样，几何形状和材料就定义好了，我们可以专注于物理场的研究。

首先，沿着光束路径穿过自由空间，从晶圆上方的激光源沿着 z 轴向下。我们有一个 40W、700nm 波长的激光器，并且光束具有标准偏差为 1.5mm 的高斯轮廓。激光器开启 75ms，然后关闭 25ms，或者激光器使用占空比为 75%，周期为 100ms 的脉冲加热。这种时间上的阶梯式加载是通过事件 接口解决的，该接口用于引入一个 离散状态 变量 ONOFF，即时间为 0 或 1。

我们不会明确地模拟激光源或通过自由空间的光束路径;我们将只对与材料相互作用的光进行建模。在顶层的边界处，折射率为 n_{top}=2.4 的材料会因为折射率的差异而有一些反射，如菲涅耳方程所示：

 
虽然这个方程适用于复值折射率，但在我们的计算中只考虑折射率的实值分量是合理的，因为折射率的虚部非常小。在界面上没有任何吸收的附加假设下(例如由于吸收材料的非常薄的涂层)，透射率为 T=1-R。这样就完成了我们在吸收介质中辐射束 接口设置入射强度 功能所需的信息，如下面的屏幕截图所示。

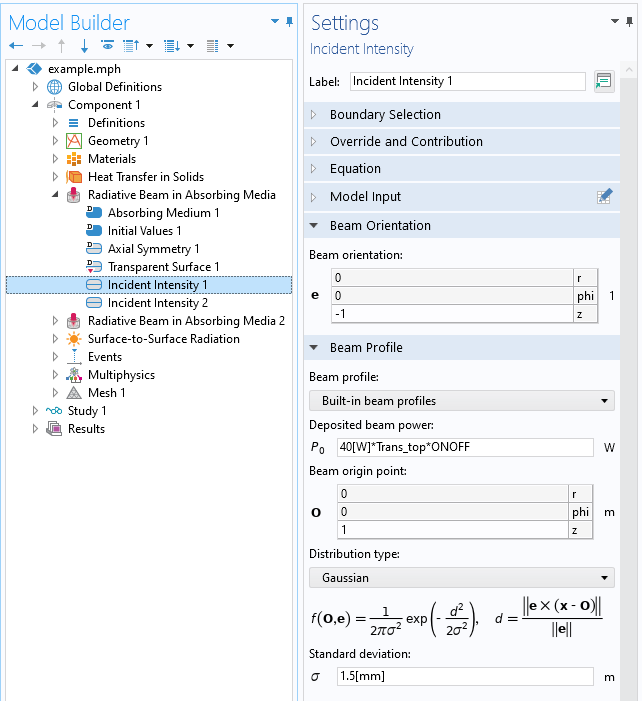
入射强度功能的设置。

当光束穿过材料的第一层时，其强度与吸收系数成比例减小，吸收系数 \kappa 由下式确定：

 
其中，k 是折射率的虚部，\lambda_0 是自由空间激光波长。吸收系数可能与温度有关，但我们将从它是一个常数开始。给定光束轮廓在顶面上的强度分布，剩下整个域的光束强度通过计算获得。

在沉积材料的顶层和底层之间的介电界面，将再次存在菲涅耳方程描述的反射和透射。光束的反射分量使用已有的 吸收介质中的辐射光束 接口进行处理，只需添加第二个入射强度 功能就可以了。可以向这个界面添加任意数量的入射强度 功能;每个都将引入一个额外的变量来求解，这些变量将被命名 rbam.I1, rbam.I2, …, 依此类推。在第二个入射强度 功能中，我们可以引入基于第一个光束强度和菲涅耳反射系数的用户定义的光束轮廓。通过改变光束方向的符号，可以完全考虑光在此接口上的部分反射，如下面的屏幕截图所示。从理论上讲，在顶部边界会有一个额外的光束反射，但是这个二次反射足够小，所以我们将忽略它。

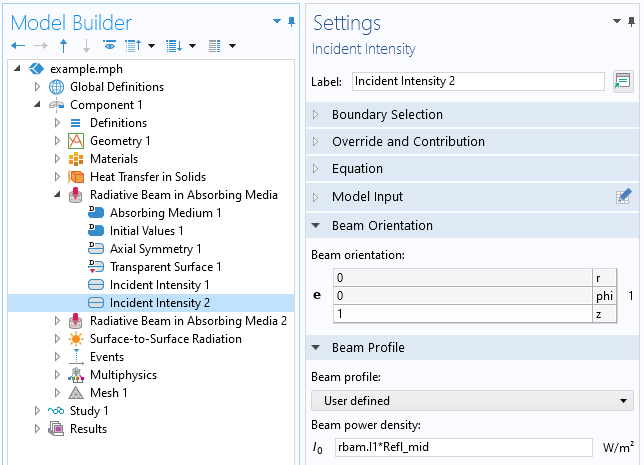
第二个 入射强度功能的屏幕截图，考虑了介电界面处的反射。

接下来，我们跟随光束穿过介电界面进入第二层半透明材料。由于跨越此边界的光强度发生了变化，因此必须添加第二个 吸收介质中的辐射束 接口，并根据菲涅耳透射率和来自第一个吸收介质中的辐射束 接口的第一束光束来定义入射强度。

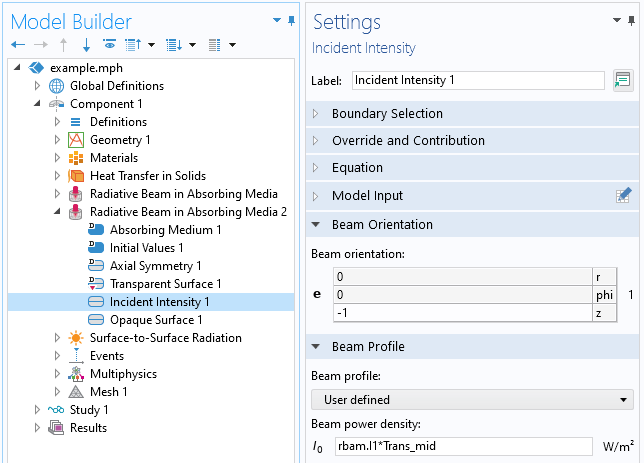
吸收介质中的辐射束接口中第二个辐射束的 入射强度特征的屏幕截图，用于底部域中的强度。

最后，让我们讨论当光线到达第二层底部并击中硅晶圆衬底时会发生什么。我们将假设硅晶片是掺杂的，因此它具有高度吸收性和非反射性。由于所有到达这个边界的光都将在足够小的距离内被吸收，因此可以说光在边界处被吸收。对于这种情况，不透明表面 边界条件将在所选边界处沉积所有能量，这就完成了激光在结构中传播时的建模。通过这些功能的组合，我们已经完全模拟了入射激光束穿过模型。现在我们可以将注意力转向热模型。

模拟温度随时间的变化

晶圆最初处于 300K 的均匀温度。所有域都有传导传热，我们假设材料之间的界面没有明显的热阻，即材料界面之间没有温差，磁通量是连续的。这种情况是软件的默认假设，但如果我们确实希望覆盖它，可以添加薄层 或热接触 功能。

在 100μm 处，层厚已经足够适用经典的傅里叶传热定律，值得一提的是，纳米级传热是 COMSOL 用户研究的一个活跃领域;例如，请参阅我们的特邀博客“动力学集体模型中的流体动力热输送”。

至于热边界条件，我们将假设晶圆位于完全绝缘的底座上，并且位于一个近真空的工艺室内。这意味着不会有传导或对流传热冷却，但会向腔室壁进行辐射传热，假设保持在 300K。接着，我们假设晶圆温度只会上升几百K，因此与入射激光相比，辐射发射将处于一个更长的波长带。这意味着，从概念上讲，我们可以使用双波段模型进行辐射传热。来自激光的入射辐射已经通过吸收介质中的辐射束 接口完全处理。较长波段的发射辐射（由于晶圆相对于工艺室壁的温度升高）可以使用单波段表面对表面辐射 接口与固体传热 接口进行建模。表面到表面辐射  接口计算所有暴露表面与周围空间之间的角系数。

值得一提的是，在这种情况下，只有在晶圆上方的小内角附近存在表面对表面辐射;其他地方对环境的角系数都是统一的。如果我们想稍微简化一下，可以不使用表面对表面辐射 接口，而是在固体传热 接口中使用表面到环境辐射 边界条件。计算时间和结果的差异可以忽略不计，因此这里我们使用更准确的方法，即使用表面对表面辐射 接口计算角系数。

我们还需要特别注意这个装置的网格划分。吸收介质中的辐射束 接口求解的是一阶偏微分方程，默认情况下使用场的线性离散化。根据吸收系数，我们知道强度会随着两层的厚度发生明显变化。我们还知道，激光束轮廓在表面上的强度变化是相当渐进的。这证明了层内具有高纵横比矩形单元的映射网格是合理的。当然，随着建模复杂性的提高，我们总是希望研究网格和求解器的相对公差细化，就像我们之前的博客文章“在 COMSOL Multiphysics® 中模拟固体瞬态加热简介“所讨论的那样。

设置完成后，我们将使用随时间变化的求解器解决这个问题，并按照求解器采取的步骤保存数据。然后，我们可以绘制出温度曲线和吸收的热量，以及一段时间内中上部点的温度，如下图所示。

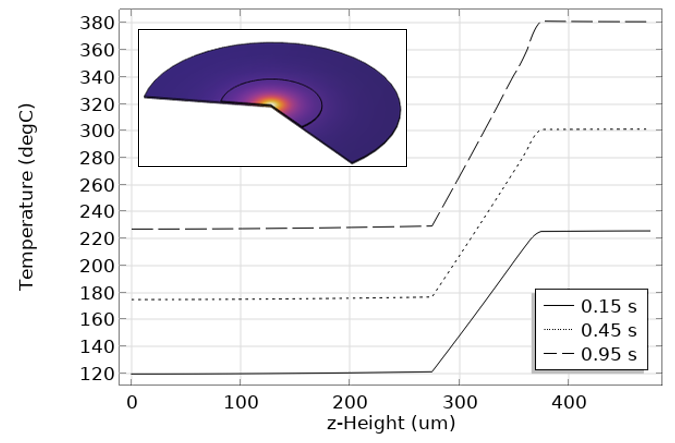
沿 z 轴的高度与温度的关系。

最后，为了说明，我们将介绍一种非线性材料，使底层的吸收系数随着温度的升高而上升。两种半透明材料的吸收系数比较如下图所示。随着非线性吸收系数的升高，材料的加热更大。由于这种材料的非线性，我们还需要细化具有非线性属性的层中的网格。

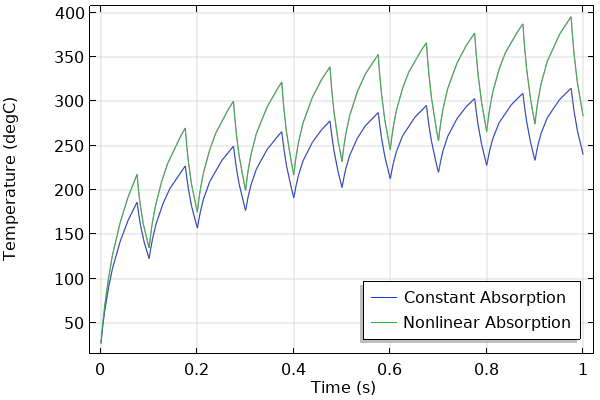
使用两种不同的材料模型比较温度随时间的变化。

结束语

我们介绍了一种解决半透明材料的加热问题的建模方法。准直辐射热源(激光)通过一组吸收介质中的辐射束 接口进行建模，该接口可以处理材料在激光波长下的半透明性质以及介电界面处的反射。脉冲热源通过事件 接口处理，较长波长的红外再辐射通过表面对表面辐射 接口处理。这种建模方法适用于半导体加工领域或准直光入射到半透明材料上的任何情况。

如果你对这些类型的模拟感兴趣，请随时单击下面的按钮下载文中讨论的示例模型：