使用 COMSOL Multiphysics® 模拟 COVID-19 的传播

地球上的所有生命都通过两个密切相关的大分子进行编码：核糖核酸（RNA）或脱氧核糖核酸（DNA）。某种意义上，我们可以说地球上只有一种生命形式。

病毒介于生命体和非生命体之间。它们具有 RNA 或 DNA，但不能自我复制，也不能在另一个活细胞外繁殖。

为了繁殖，病毒必须与活细胞接触，它必须适合宿主细胞的受体，并且必须打开宿主细胞的膜。然后，病毒可以注入其 RNA 或 DNA 并劫持宿主细胞的新陈代谢，以产生新的病毒粒子。

由于病毒粒子在活细胞外存活的能力非常有限，因此其传播的主要机制是通过活生物体之间的接触。如 SARS-CoV-2（导致新型冠状肺炎爆发的病毒，COVID-19），它必须在人与人之间直接或间接传播。世界卫生组织（WHO）已将 COVID-19 列为大流行病。

我们有可能了解大流行的进程吗？有多少人会被感染？有多少人会死亡？下面，让我们看看预测 COVID-19 传播的数学模型是什么样的。

COVID-19 的数学模型

所谓的 SEIR 模型是可以合理预测传染病在人与人之间传播的一种简单模型，该模型于 1920 左右首次公开发表（参考文献1 ）。此模型将受传染病影响的人群分为四类，分别用相应变量来描述每类人群的数目。

S =易感者

E =潜伏者

I =感染者

R =康复并具有免疫力的人

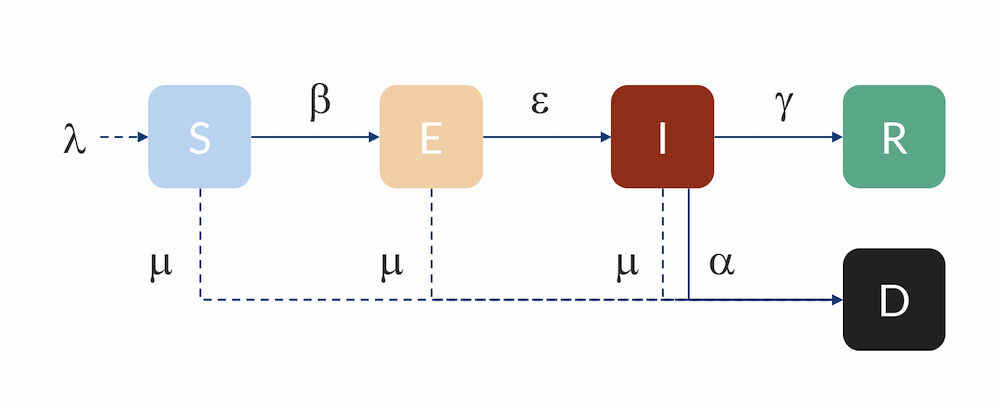
区间模型：个体以速率 β 从 S 流向区间 E ，以速率 ε 从 E 流向 I，以速率 γ 从 I 流向 R，还可以速率 α 从 I 流向 D（死亡）。这里假定 R 中的个体是免疫的，并且在模型计算时不会返回 S 。新生儿的流入量用 λ 表示，自然死亡率用 μ 表示。

变量 S，E，I 和 R 的单位为个体的数量。当易感者以某种形式接触了感染者，可能会成为潜伏者。成为潜伏者的概率，与人群中感染者的占比与易感者总数的乘积相关。经过简单的推导，易感人群被传染的速率为：

(1)

其中 β 是传染率。

β（单位：1人 /天）与基本传染数 R ₀和感染者具有传染性的平均天数（在被隔离或自我隔离之前）有关，n_id：

(2)

R ₀  称为基本传染数（无量纲），它描述了感染者在康复之前与易感人的每次接触（当人群中完全没有免疫力时）的疾病传播。任何缓解或隔离措施都旨在通过减少传染率 β 或及时隔离感染者，来降低传染数。

对于较短的（非季节性）流行病模拟，我们可以假设自然死亡和出生处于平衡的恒定人口。然后，随着新暴露病例的增加，易感个体的数量减少，其中 N 表示人口规模：

(3)

相应地，上述方程式右侧的项是方程式中潜伏者 E 的源项。但是，为描述从潜伏者转变为感染者的过程 E ，该方程式也具有负项。

(4)

此处，ε 表示一旦暴露就发展成传染性的速率，以 1 人/天为单位。该速率与潜伏期的长短成反比。

感染者的数量 I ，每天随着 ε  Ë 的增加而增加，但随着个体被隔离，康复个体或死亡个体的速度逐渐减少。系数 γ 表示人们被隔离或康复的比率。感染率与感染的天数成反比：

(5)

对于因感染病毒而死亡的比率 α I 的比率和感染变量 I ，还可以用以下方程表示：

(6)

对于变量R，可以用下列方程表示不再受感染的个体：

(7)

对于死亡人数 D ，可以用下列方程表示：

(8)

展平曲线

我们可以从一个简单的模型开始，其中不考虑潜伏者。即，易感者遇到感染者，不经过潜伏者，直接被感染。在我们的模型中，这将对应于非常大的 ε 值。然后，我们可以将其与 Michael Höhle 的博客文章进行比较，因为他已经求解了相同的数学模型（参考文献2）。输入数据如下：

N = 100 万个人

R ₀ = 2.25，基本传染数

Ñ _ID =5 天

最后，我们需要初始条件：

S ₀  = N –  I ₀，易感人群

I ₀  = 10 个感染者

在第一种情况下，Höhle 进行了模拟。在该模拟中，流行病得以继续发展而不采取社交限制措施。在第二种情况下，Höhle 假设在有 100 万人的城市中，当局采取了减少有效传染数的行动，例如，不允许进行大型人群聚会（举办体育赛事、音乐会等）。第一步是在疾病流行 28 天后，通过限制社交互动，将有效传染数减少到 1.35。当限制措施持续 5 周后，放松限制，有效传染数升高到1.8。下图显示了两种情况：情况1（不限制社交）和情况2（R ₀ 减少））。我们可以看到模拟结果与Höhle的结果非常吻合。

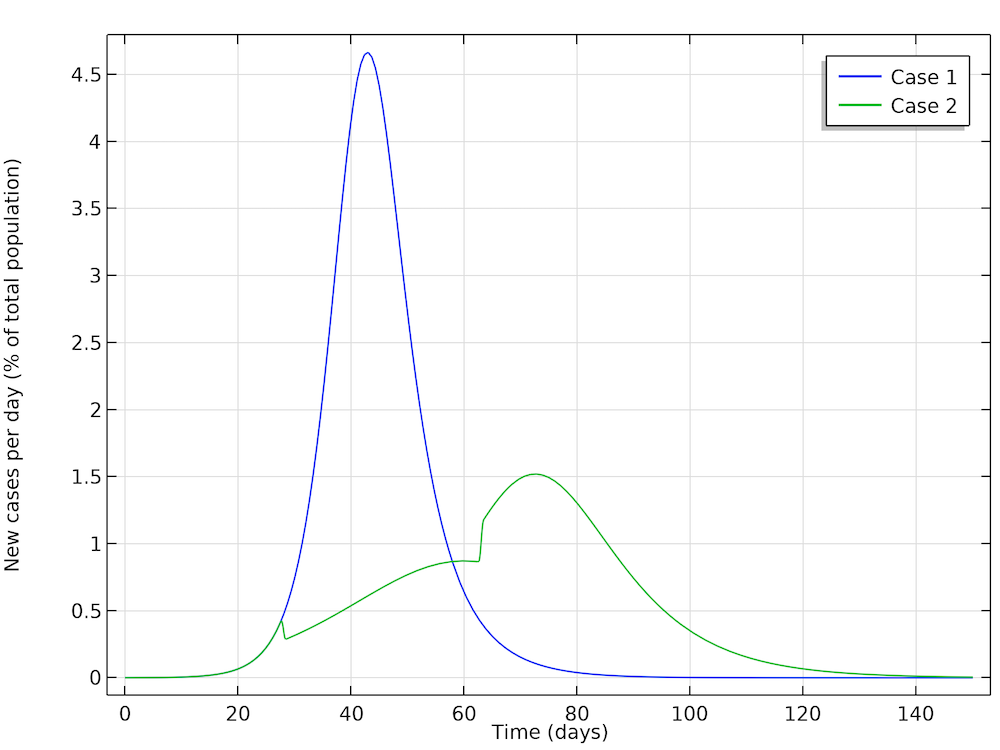
此处获得的结果与 Höhle 的结果非常吻合。在第 28 天采取社交限制措施后，新病例（绿色曲线）突然减少，当限制措施放松后，绿色曲线突然跃升。

根据第二种情况，Höhle 得出一个有趣的结论，为减少新增病例而采取的社交限制措施不仅减少了传染病流行期间新增病例的数量，而且还减少了整个流行病期间的感染者总数。 结果如下图所示。在第一种情况下，整个流行病期间被感染的人口比例为 85％，而在第二种情况下，这一比例仅为 68％。因此，采取社交限制措施不仅​​可以暂时减轻医疗保健系统的负担，而且还可以减少流行病患者的总数。

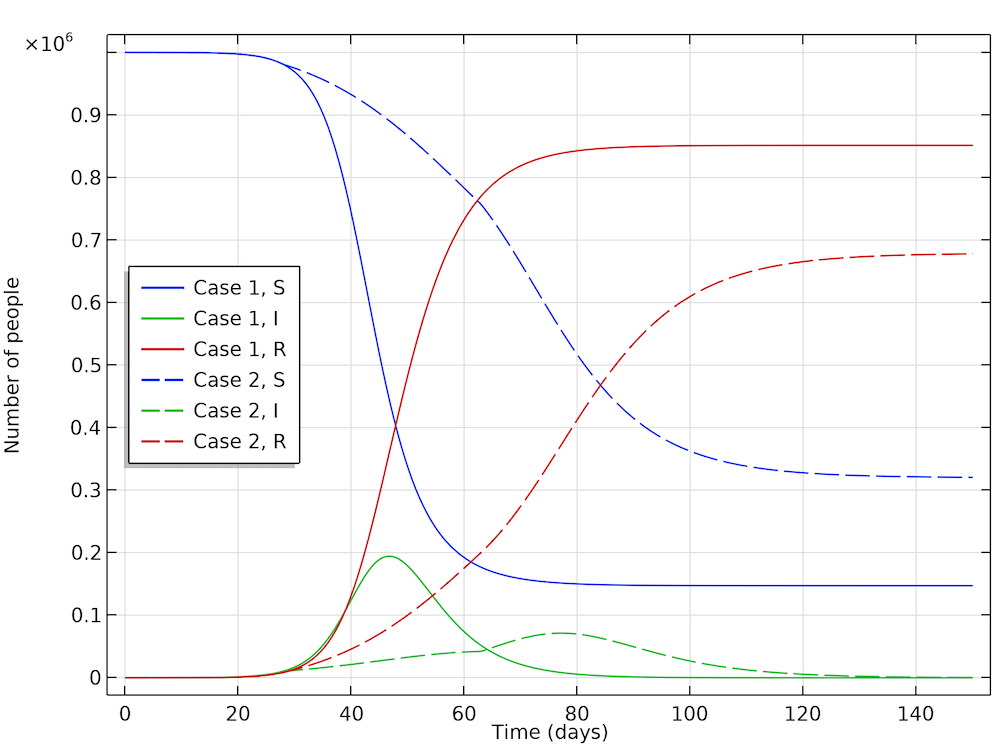
如果不采取任何措施，则被感染的人群比例为85％，这可以从恢复曲线中看到（红色，实心）。在采取措施的情况下，有68％被感染（红色，虚线）。

考虑不同人群分布的流行病发展过程计算

对于湖北，瑞典和美国，我们可以使用稍微更高级的模型，即所谓的Erlang–SEIR模型（参考文献3）。通过将 E 和 I 人群划分为子类，每个子类中个体的停留时间假设遵循 Erlang 分布，并且指定的平均停留时间与子隔间数 k ^E和k ^I 成正比，与子隔间 ε 和 γ 的传输速率成反比。该模型可以说明以下事实：不同子类之间的流量存在特定分布，例如，由于潜伏者在该国不同地区的不同时间进入，增加子类的数量会使分布集中在均值周围，实际上延缓了从 E到I 以及从 I到 R 和 D 的进程。

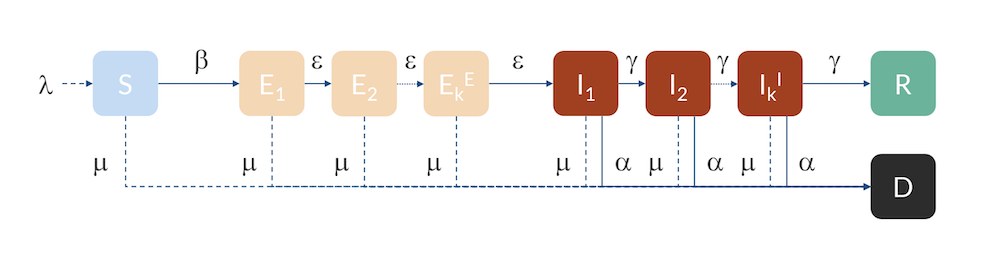
具有 E 和 I 子隔间的 Erlang–SEIR 模型。

COVID-19在中国湖北的传播模拟

假设死亡率为0.66％（参考文献4），感染者平均在第3天被隔离，从症状发作到死亡的平均时间为18天，我们就可以适应流行病的开始、传播，以及在Erlang分布中暴露状态下从湖北报告的数据的平均时间。

2019年1月22日，当局实施了封锁措施，并在该月底进行了测量，结果显示基本传染数明显下降（参考文献5） 。

如果我们实施这样的封锁措施，并且如果我们将该限制措施的影响在1月23日开始生效，我们将获得以下结果。

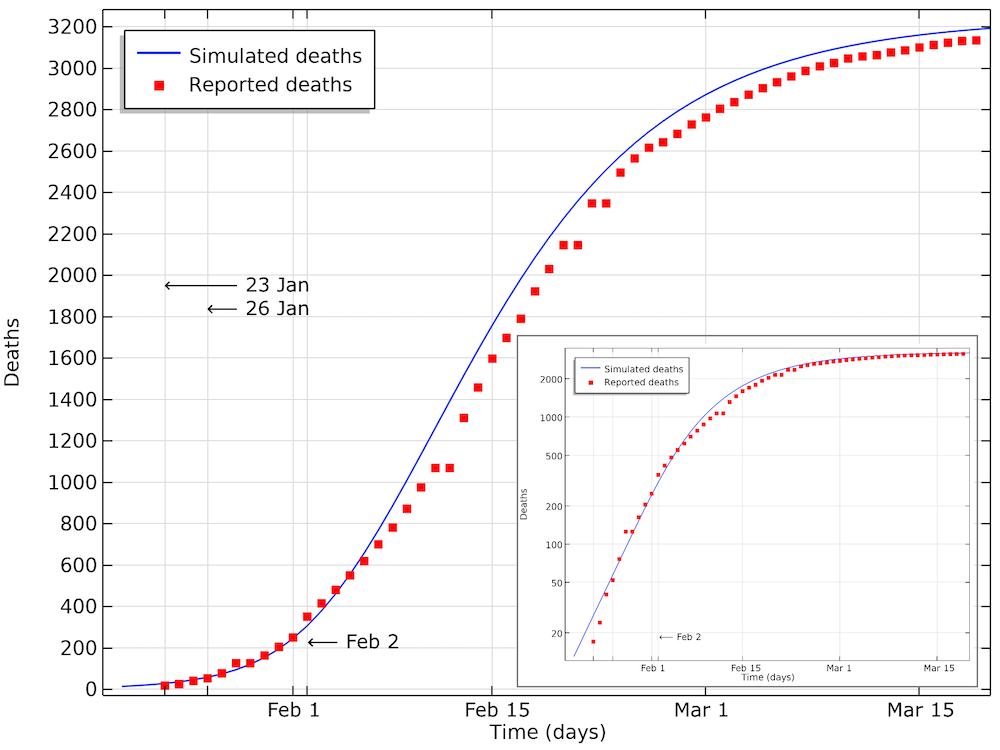
该图为 COVID-19 死亡人数建模数据与湖北报道数据的比较。我们可以看到该模型与数据非常吻合，仅有 0.5~1 天的微小偏移。这个偏移可能来自于数据是以每日来统计的。小图以对数标度显示 y 轴的相同数据。

从上面的图表中可以看出，到2月2日，累积死亡人数呈对数图中的线性增长，直到大约400人死亡。2月3日之后，死亡人数的增长速度下降，因此增长不再是指数级的。这主要源于社交限制的措施。在这一阶段尚未发现具有免疫力病例的影响，这也将降低 COVID-19 的有效传染数。

下图显示了疫情进程中，潜伏者、传染者、康复者和死亡的人数情况。我们在如下几个时间点插入了额外的网格线：（1）在实施社交限制措施的1月23日；（2）1月26日中午，当感染人数达到上限时；和（3）2月3日，即死亡人数最多时。请注意，康复病例数是指不再具有传染性并且正在恢复的病例。在医院，此类患者要等一到两周后才能出院。

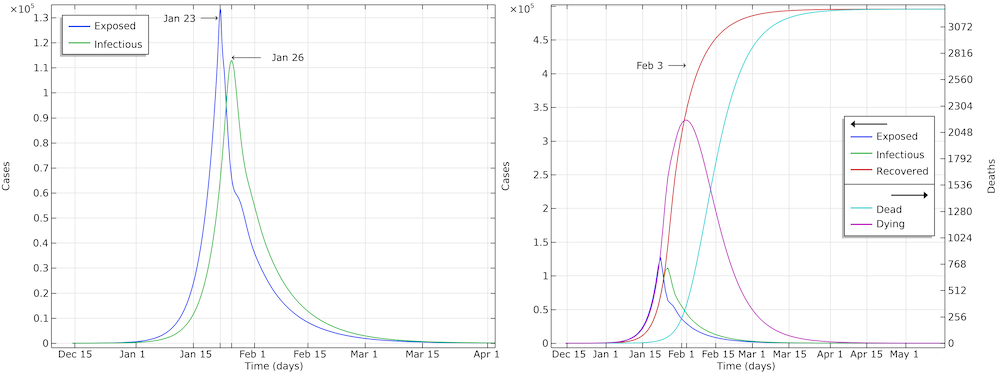
湖北疫情的发展。随着时间的推移，预计受感染的人数将接近 500,000 人。

通过参数估计得出的湖北数据的基本传染数为 3.03，高于 WHO 的报告，但仍在其他研究报告的范围内（参考文献6,7 ）。社交限制使有效传染数降低到约 0.56，这是我们通过拟合死亡曲线获得的。这个数字低于其他地方的报告，但与当地流行病的迅速结束相一致。

瑞典：保持社交距离

瑞典选择了与湖北和大多数其他国家不同的策略：限制社交互动，但与湖北实施的完全封锁相比，还相距甚远。建模过程与湖北也略有不同，主要是因为其最早的感染和潜伏病例均来自于意大利和奥地利的输入。我们使用了与冬季假期相关的输入案件的分布，这些案件在全国不同地区分布了三周。但是，在2月17日至3月1日的两周内，斯德哥尔摩地区的居民返回家园时，大多数旅行者很可能已受呈指数级增长的意大利爆发疫情感染。

以下是模拟死亡人数与报告的死亡人数比较。4月2日的病例数仍呈指数增长（对数图中呈线性）。

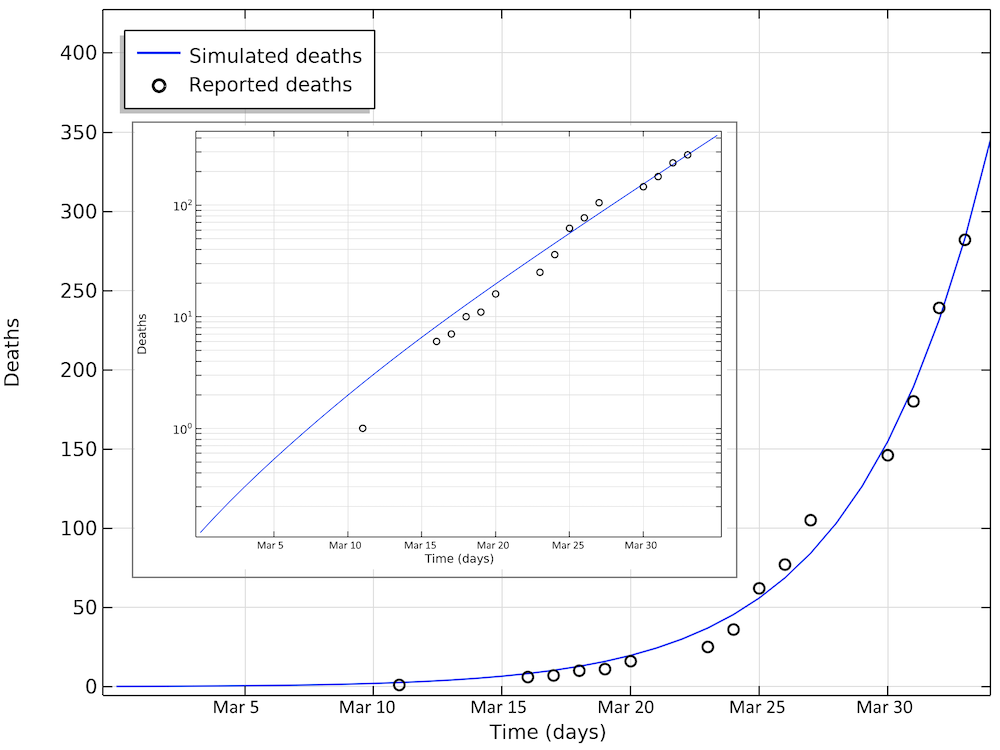
瑞典死于 COVID-19 的人数。第 33 天最新报告的值对应于 4月2日。小图为以对数刻度显示 y 轴的相同数据。

通过参数估计得到的瑞典数据，有效传染数为2.95，接近从湖北获得的数据（3.03）。输入病例总数约为500。

自3月16日左右以来，瑞典一直实施社交互动的限制，但主要是以建议的形式出现，可能没有立即产生效果，因此死亡人数尚未降低。我们在此模型中假设这些限制已于3月20日全面生效。

让我们假设两种情况：第一种情况，社交互动限制将有效传染数减少到基本传染数的0.35倍；第二种情况，有效传染数减少到基本传染数的0.30倍。第一种情况将有效传染数降低到1.03；也就是说，每个受感染的人平均感染1.03个人。第二种情况将有效传染数降低到0.88（低于1），这意味着十个受感染者中，只有九个（几乎）可以在恢复之前“替代”自己（平均）。

两种情况的限制措施幅度均不及湖北的限制幅度大，这是合理的假设，因为瑞典尚未实施全面封锁。

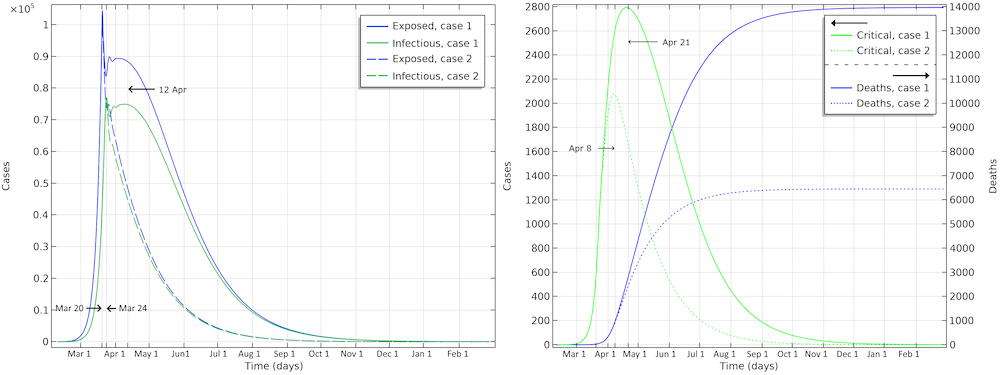
在第一种情况下，约有210万人被感染，约占人口的20％（请参见下图）。截至4月2日，已感染或已感染的人数将为280,000人，几乎是确诊病例的60倍。第二种情况导致截至4月2日，约有260,000人被感染，但是该流行病的进展速度大大减慢并受阻，导致在流行病消亡之前的某个时候，只有不到一百万的人被病毒感染。

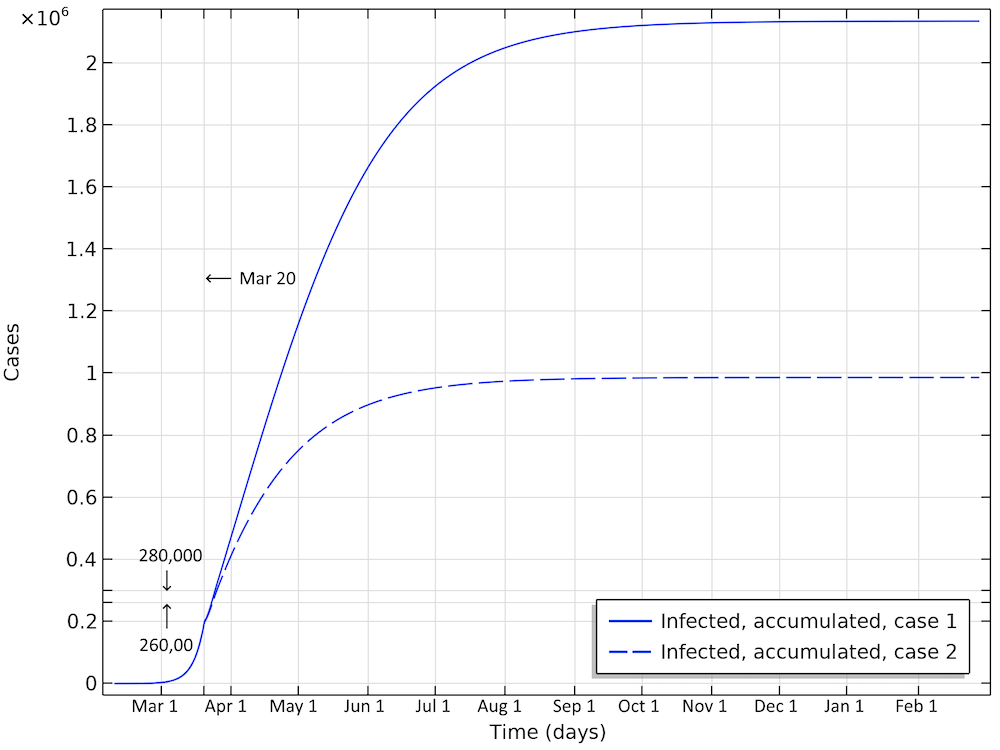
两种情况下，瑞典累计感染总人数。这是在整个流行过程中将被感染的所有个人数的总和。

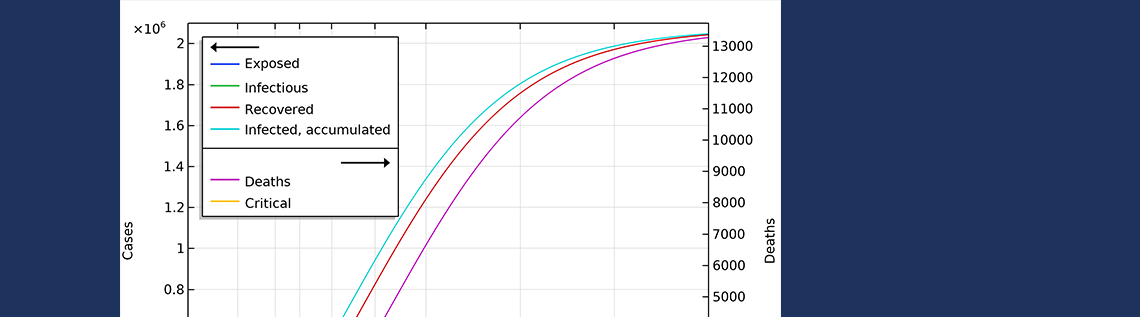
第一种情况下，最终死亡人数超过13,000。另外，严重疾病和每日死亡人数的峰值在4月21日达到峰值。如下图所示，每天的死亡人数将达到155例/天。第二种情况下，最终约有6500人死亡，并且死亡人数在4月15日左右达到峰值，每天约有115人死亡。

假设3月12日至3月16日左右采取的行动，瑞典的流行病预计发展情况。假设瑞典当局采取行动的效果不及湖北采取的行动有效。

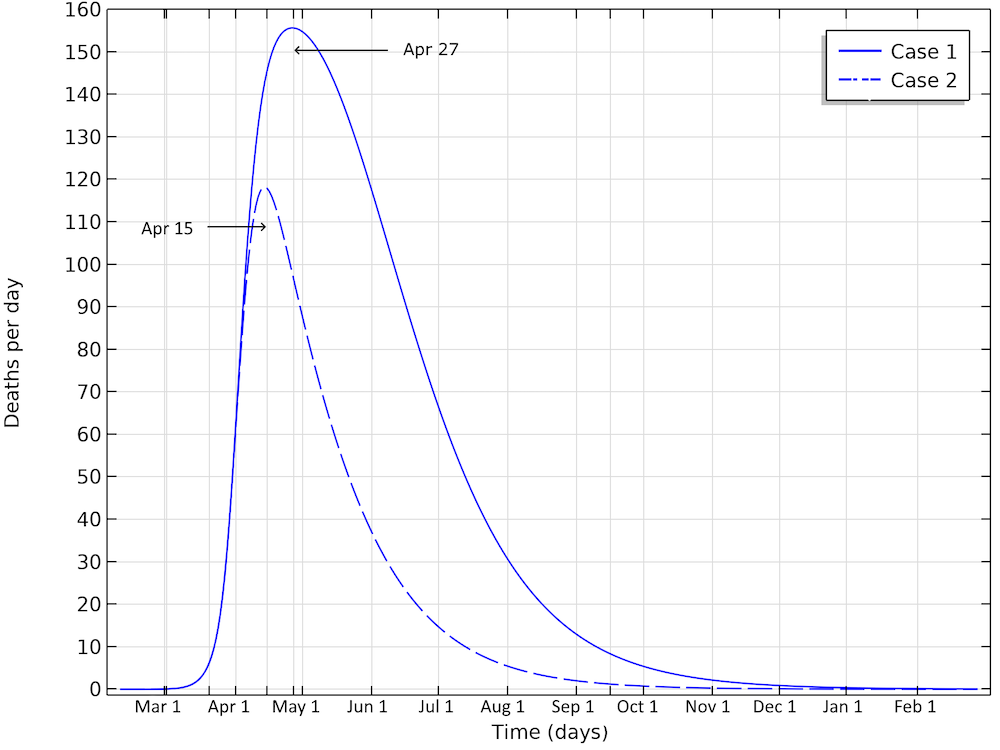
在第一种情况下，瑞典的死亡人数将在4月27日左右达到峰值，在第二种情况下，死亡人数将在4月15日左右达到峰值。

只要略微加强“社交距离”，将有效传染数从1.03降低到0.88时，就可产生巨大变化。这意味着在整个流行病期间，将会减少6500人死亡。

美国：大规模隔离

在我们的研究中，假设美国的所有感染病例均来自国外，则感染个体的数量及其流入美国的数量是可根据当时美国境外感染者的分布情况进行参数估计。我们使用了截至3月31日的死亡人数来进行参数估计。与瑞典和湖北相比，美国的一个特殊问题是该流行病的区域差异更大，而且不同的州在不同时间，采取了不同的行动。

下图显示了截至3月31日（图表31天）的模拟死亡和报告死亡。同样，在这种情况下，我们看到死亡人数呈指数增长，与对数图上的线性增长相对应。

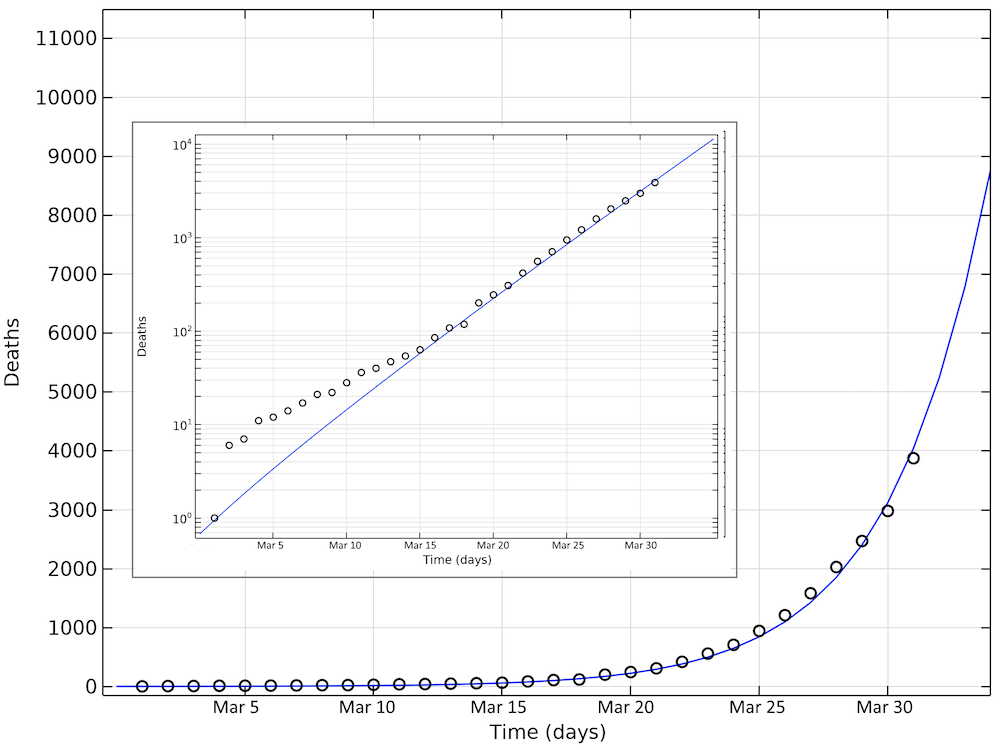
截至3月31日美国的模拟死亡人数和报告死亡人数。请注意，在对数图中，当死亡人数较小时，模型与报告的病例之间的偏差看起来较大数目下的更大。内嵌图为以对数标度显示 y 轴的相同数据。

通过参数估算得出的美国数据的基本传染数为 2.97，与瑞典（2.95）和中国湖北（3.03）的拟合值一致。那么，输入案件的总数将约为 8000 例。

同样在美国，我们可以假设两种情况：一种与瑞典的情况类似，社交限制措施将有效传染数减少到基本传染数的0.3倍（瑞典的数值），另一种情况将有效传染数减少到基本传染数的0.185倍（中国湖北的数值）。这也是合理的，因为美国实施了介于瑞典和湖北之间的限制措施。不是完全封锁，而是实施了比瑞典更严格的大规模隔离。这样得出的有效传染数分别为 0.89 和 0.55 。

第一种情况预测，在流行病消亡之前将有近2000万美国人受到感染（请参见下图）。到4月1日，受感染人数将达到600万。在第二种情况下，大约有500万人受到感染。这大约是所报告的确诊病例的25倍，这听起来还是很高，但并非不可能，因为仅对一小部分人群进行了检测。

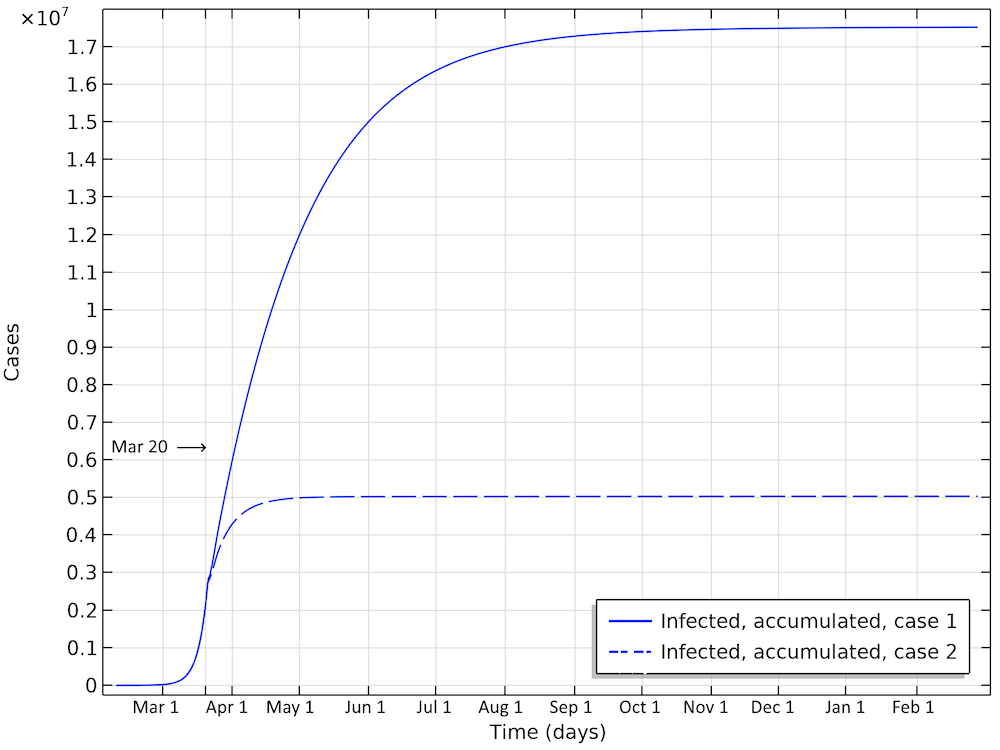
两种情况下，美国累计的感染总数，这是在整个流行过程中将被感染的所有个人的总数。

在第一种情况下，美国的死亡人数为115,000（请参见下图）。感染人数最多的应该是3月24日左右。重症监护中的危重病例数将在4月9日。在第二个病例中，与湖北的限制相同，重症监护患者数将在4月1日左右达到峰值。流行病结束前的死亡人数约为33,000。

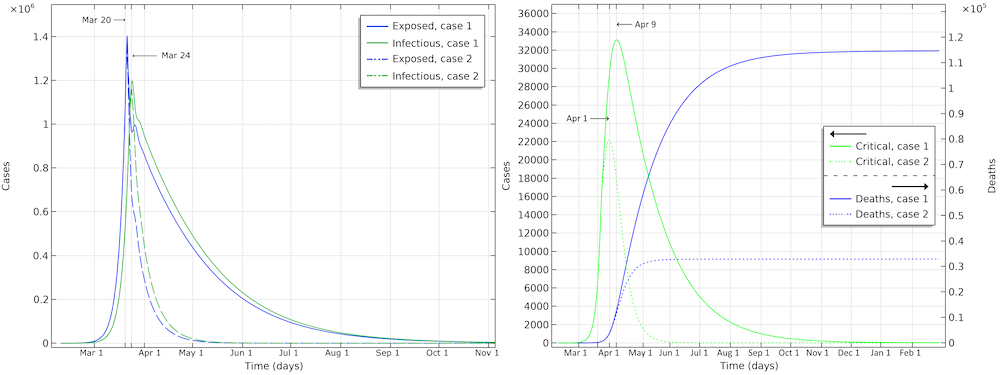
两种情况下的潜伏者、传染者，峰值人数和死亡病例，有效传染数降低至 0.89（第一种情况），有效传染数降低至 0.55（第二种情况）。

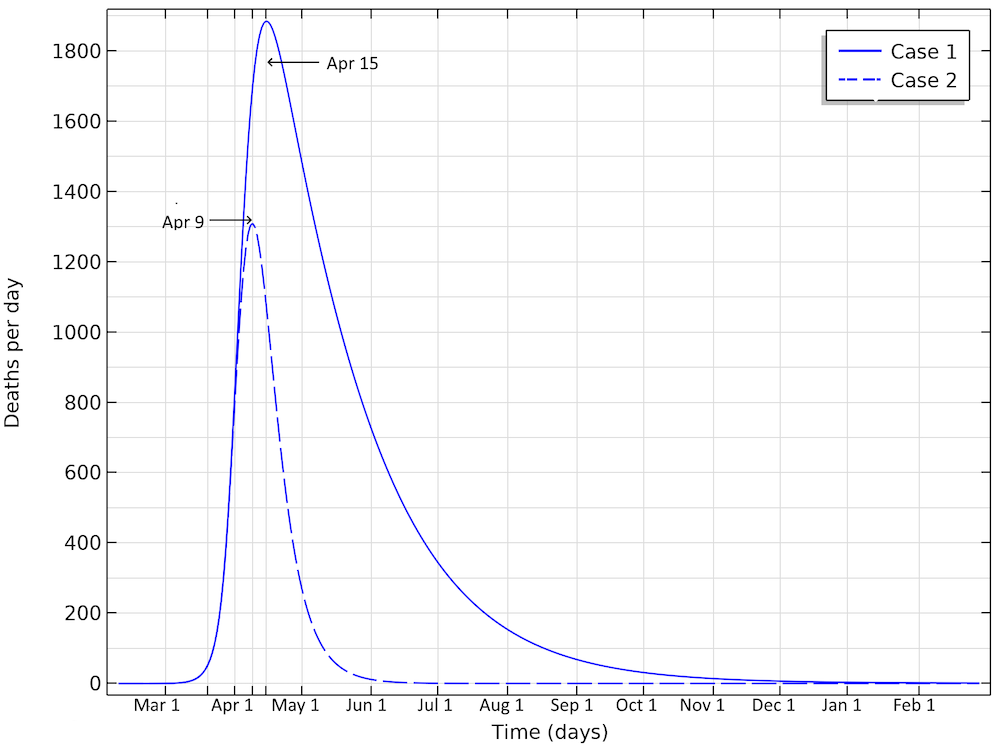
根据我们的模型，第一种情况下，美国的死亡人数将在4月15日左右达到峰值；第二种情况下，将在4月9日左右达到峰值。

在第一种情况下，每天的死亡人数将在 4 月 15 日左右达到高峰；在第二种情况下，每天的死亡人数在4月9日左右达到峰值。这分别对应于两种情况下每天的死亡人数分别低于1900或1300。我们可以看到，第二种情况下，每天的死亡人数更高。而且这个数字还会增加。如果我们将有效传染数减少到 1.04（减少 0.35 倍），即仅在上述案例1之上，那么在流行病结束之前，我们可能会有350,000 例死亡人数。该模型清楚地显示了社会限制措施的巨大影响，不仅减少了峰值死亡人数，而且在流行病结束之前，受感染个体的总数也大大减少。

如何使用模型

此处给出的结果不应解释为预测。它们是来自简化现实模型的结果。我们不考虑人口统计。例如，人口中的年龄分布对疾病的死亡率有很大的影响。

疫情进展处于不同阶段的被研究国家的地理差异也无法得到准确的解释。人们在一个国家不同地区之间的旅行方式也会影响这一流行病的进展。

此外，我们很难预测中国，瑞典和美国民众采取的行动对模型输入的影响。政府组织，例如中国疾病预防控制中心，瑞典公共卫生局和美国疾病控制中心（CDC），拥有更复杂的模型来说明年龄分布，流行病的发生地点，城市之间迁移的数据，国家之间迁移的数据以及其他人口统计数据。他们还拥有有关病毒和疾病本身的更好数据，例如在不同条件和年龄分布下的潜伏时间和繁殖数量。

但是，使用此处介绍的模型仍然有一定的借鉴意义。他们了解这种流行病的发展趋势。这些模型还直观地表明了保持社交距离和避免不必要的社交互动，可以降低 COVID-19 的有效传染数，减少重症监护患者的高峰期并减少总体流行影响。此外，各国和国际性组织的公共卫生相关部门，可将 Erlang–SEIR 模型作为重要的研究工具，并在此基础上开发更为细致和专业的数学模型，为各个国家和城市服务。

下载模型和应用文件

通过下面的按钮下载用于 COVID-19 流行模型的SEIR模型和演示应用程序。请注意，要访问MPH文件，您必须登录到 COMSOL Access 帐户并具有有效的软件许可证。

参考文献

1. H. Weiss, “The SIR model and the Foundations of Public Health”, MATerials MATemàtics, vol. 2013, no. 3, pp. 1–17, 2013.
2. M. Höhle, “Flatten the COVID-19 curve”, Theory meets practice…, 2020.
3. W.M. Getz and E.R. Dougherty, “Discrete Stochastic Analogs of Erlang Epidemic Models”, Journal of Biological Dynamics, vol. 12, pp.16–38, 2018.
4. R. Verity, L.C. Okell, I. Dorigatti, P. Winskill, C. Whittaker, et al., “Estimates of the severity of coronavirus disease 2019: a model-based analysis”, The Lancet Infectious Diseases, 2020.
5. A.J. Kucharski, T.W. Russell, C. Diamond, Y. Liu, J. Edmunds, S. Funk, R.M. Eggo, “Early dynamics of transmission and control of COVID-19: a mathematical modelling study”, The Lancet Infectious Diseases, 2020.
6. R. Li, S. Pei, B. Chen, et at., “Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2)”, Science, 2020.
7. Y. Liu, A.A. Gayle, A. Wilder-Smith, and J. Rocklöv, “The reproductive number of COVID-19 is higher compared to SARS coronavirus”, Journal of Travel Medicine, vol. 27, no. 2, 2020.

请注意，这不是同行评审的出版物，也没有由任何流行病学家准备或与任何流行病学家商量或未根据任何流行病学标准进行准备。此外，未知的各种各样的情况可能会影响所讨论模型的准确性，尤其是关于将来的进展。