对流-固耦合问题进行拓扑优化的新方法

工程师在开发涉及流-固耦合的系统（例如，桥梁、飞机和生物医学应用）时，可能会希望在设计的早期就使用拓扑优化。然而，许多拓扑优化方法仅适用于学术范围内的流-固耦合问题。本文，研究人员开发了一种新的方法来帮助解决这个问题…

流固耦合和拓扑优化

流固耦合

流固耦合描述了流体动力学定律和结构力学定律之间多物理场的相互作用。在设计各种系统（例如汽车、飞机和航天器）时，考虑 流固耦合尤为重要。如果忽视这些影响，可能会导致灾难。

1940 年 11 月，在华盛顿州塔科马市发生了一起悲剧，Tacoma Narrows 大桥在开通仅四个月后就倒塌了。它在被摧毁时是世界上第三长的吊桥，连接着 Tacoma 和 Kitsap Peninsula 岛。

刚开始，许多人认为该桥梁倒塌是由于共振，但后来人们了解到这是由于气动弹性颤振导致的。这种大规模的结构设计失败证明了研究流固耦合的重要性，尤其是在设计大跨度桥梁时。（Tacoma Narrows 大桥后来被重建成一对双悬索桥）。

流固耦合在血液流动建模中也发挥着重要作用。例如，生物医学工程师可以通过模拟流固耦合来准确预测人类心脏瓣膜的行为，并解决各种心脏健康问题。

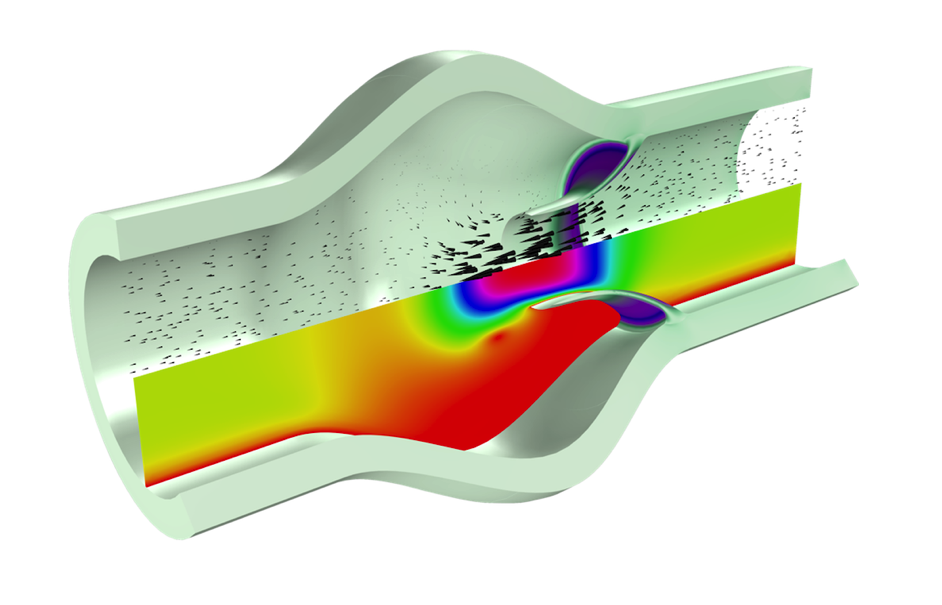
模拟心脏瓣膜打开的流固耦合模型，图中显示了速度大小和表面结构应力。红色表示低速（阀门下游）和高速（中心孔口），紫色表示高应力值。

拓扑优化

拓扑优化是三个主要优化类别之一（另外两个是参数优化和形状优化）。

拓扑优化是一个非常强大的工具，它可以帮助我们为给定目标和约束条件的工程结构生成新的拓扑。但是，它的用途通常仅限于单物理场设计（参考文献 1）。

为了解决这个问题，来自圣保罗大学（University of São Paulo）和加州大学圣地亚哥分校（University of California San Diego）的研究人员着手开发了一种新方法，将拓扑优化方法应用在结构的流固耦合分析中。

将新的拓扑优化方法集成到 LiveLink™ for MATLAB^®

在圣保罗大学，研究人员正在努力推进天然气的可持续利用。由于他们的大部分工作都涉及流固耦合问题，因此圣保罗大学多物理场系统优化实验室开发了一种新方法，即通过 LiveLink™ for MATLAB^® 接口产品将拓扑优化方法——二元结构拓扑优化法（Topology Optimization of Binary Structures，TOBS）集成到有限元软件包 COMSOL Multiphysics^® 软件中。

二元结构拓扑优化方法（参考文献2）最近由 Renato Picelli（曾是英国卡迪夫大学的博士后助理）和来自加州大学圣地亚哥分校的 Raghavendra Sivapuram 独立开发。该方法使用了顺序近似问题、敏感性过滤、整数线性规划，以及在处理与设计与多物理场问题时非常有用的二进制设计变量。圣保罗大学的多物理场系统优化实验室团队开发了一个基于几何修整（geometry trimming，GT）的框架，创建了用于流体结构设计的 TOBS-GT 方法。（您可以在参考文献1 中了解有关此方法实施的更多信息。）

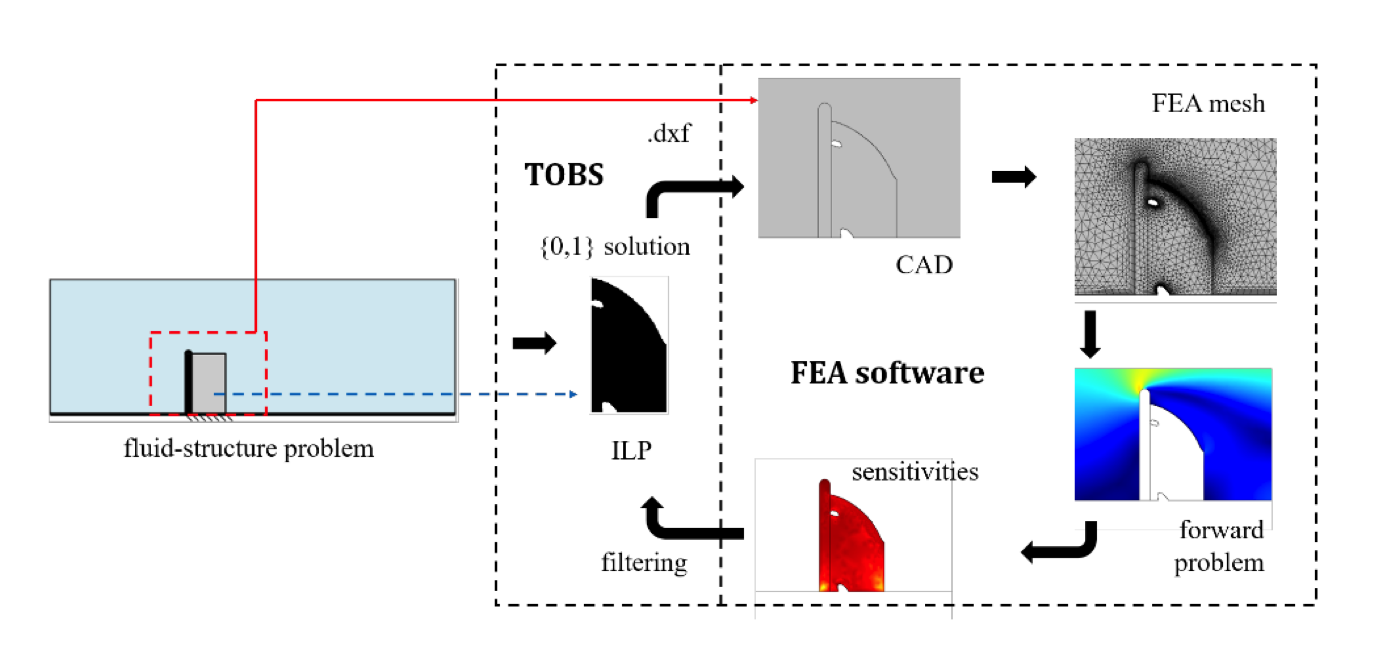
用于流体和结构设计的 TOBS-GT 算法。

Shahin Ranjbarzadeh是圣保罗大学的博士后，同时也是圣保罗大学多物理场系统优化实验室团队成员，他表示：“一开始，二元结构拓扑优化方法只是应用于结构的拓扑优化。通过开发 TOBS-GT方法，我们将这一想法应用在涉及层流、湍流和非牛顿流的流固耦合问题。”这项工作代表了在流固耦合问题中考虑整数线性规划的第一次尝试。

将二元结构拓扑优化方法与 LiveLink™ for MATLAB^® 结合使用的主要好处是结果中没有灰度，因为二元结构拓扑优化方法基于二元设计变量 (0,1)。“二元结构拓扑优化方法基于 0 和 1，所以在拓扑优化结果中没有任何中间值，” Ranjbarzadeh 解释道。此外，使用 TOBS-GT 方法，我们可以根据物理场要求调整网格。

为了让您更好地了解所提方法的特点，研究人员分享了他们 2020 年发表在 Springer Nature 上的论文中使用的示例，这是他们首次发表该方法的文献。

气动装置

“当我们写第一篇论文时，我们正在寻找一个真正的应用。最终，研究人员选择展示该方法在流固耦合载荷下降低线弹性系统柔度的能力，所有这些载荷都受到体积限制。”Ranjbarzadeh 说道。所有的示例显示了仿真结果的平稳收敛。

研究论文中的一些示例是基于气动装置的。

Ranjbarzadeh 说：“我认为这种方法将有助于预测气动设备的故障，例如压缩机或旋转机械中的故障。”

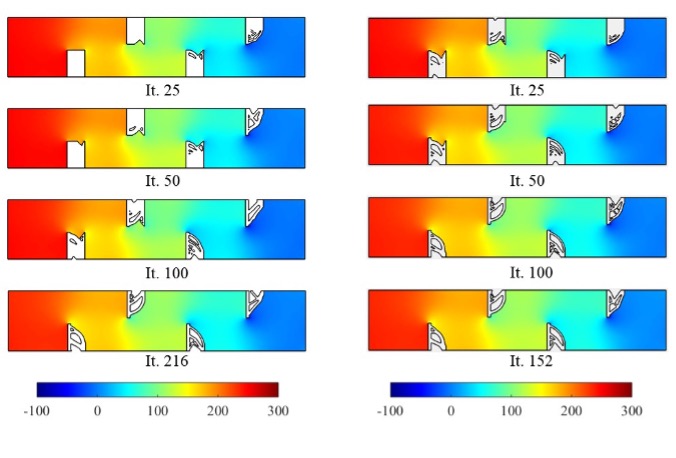
流固耦合拓扑结构优化解决方案可实现最小结构柔度，受单一全局体积约束（左）。密封拓扑优化解决方案可实现最小结构柔度，受四个独立的体积约束，每个壁一个约束（右）。两幅彩色图都突出显示了流体压力场（单位：Pa）。

3D流固耦合拓扑优化

除了已发表论文中展示的结果之外，他们还对流固耦合拓扑优化进行了 3D 模拟，如下示例所示。

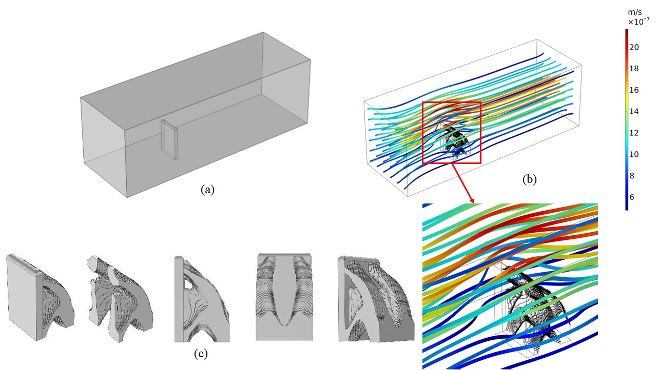
3D 流固耦合 拓扑优化域 (a)、与流体速度流线 (b) 的最小结构柔度的 3D 解决方案，以及层流载荷下 3D 优化结构的不同视图 (c)。

未来研究

文中介绍的方法也可用于对其他的多物理场耦合执行拓扑优化。

目前，研究人员正在开展一个新项目，以使用相同的方法开发流体拓扑优化。“我们正在做的事情非常简单。该程序分为两部分，” Ranjbarzadeh 说。首先，他们正在使用 COMSOL Multiphysics 解决 CFD 问题。通过定义几何形状、网格划分并计算灵敏度分析接下来，他们将灵敏度提供给 MATLAB^® 中的优化点网格（TOBS 方法是在 MATLAB^® 环境中编写的），从这里开始，该团队开始计算和分析拓扑优化。重复这个过程，直到优化问题得到解决。

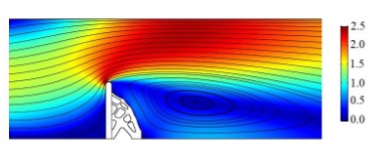
正在进行的研究涉及流固耦合拓扑优化解决方案，具有最小结构柔度的结构在湍流载荷下流体的速度流线（注：该论文正在修订中）。

参考文献

1. S. Ranjbarzadeh, R. Picelli, R. Sivapuram, R. S. Gioria, E. C. N. Silva, “Topology optimization of binary structures under design-dependent FSI loads“, Structural and Multidisciplinary Optimization, vol. 62, pp. 2101–2116, 2020.
2. Sivapuram, R. Picelli, “Topology optimization of binary structures using Integer Linear Programming”, Finite Elements in Analysis and Design, vol. 139, pp. 49–61, 2018.

MATLAB 是 The MathWorks, Inc.的注册商标。