
你有没有遇到过这种情况:你想为一个物理问题添加某个边界或域条件,但是找不到 COMSOL 软件中内置的功能?今天,我们将向您展示如何使用弱贡献特征来实现非标准约束。实际上,弱贡献是 COMSOL 软件内部用于施加内置域和边界条件的功能。它提供了一种灵活且不依赖物理场的方式,来扩展 COMSOL Multiphysics® 软件的适用性。
弱贡献简介
在 COMSOL Multiphysics 中解决的许多问题都可以看作是寻找能使某些量最小化的函数。例如,在弹性平衡问题中,我们要寻找的是使总应变能最小的位移。在关于变分问题和约束系列博客中,我们介绍了如何使用弱形式偏微分方程 接口来解决有约束和无约束的变分问题。我们使用了一个广义的约束框架来处理对解的各种限制。在该系列文章中,我们向您展示了如何实现无约束和有约束的问题。
通常,要最小化某个量是很好理解的,而在具体的问题中,我们要指定的是约束设置。理想情况下,我们不应该在无约束问题上浪费时间做无用功。通常,约束是边界条件,但有时它们可能是在每个点或通过解的积分来满足的要求。虽然 COMSOL Multiphysics 中内置了多个边界条件和其他约束选项,但您可能时不时的需要添加一两个新约束。今天,我们将介绍如何使用弱贡献实现这一点。
在这篇博文中,我们将:
- 快速回顾一下为变分问题添加约束的情况
- 使用弱贡献将非标准约束添加到一些著名的方程中
- 将这个数学思想与一些更具有物理实际意义的实现场景进行比较
为极值问题添加约束
在关于变分问题和约束的系列博客中,我们详细讨论了该主题的分析和数值模拟以及如何在 COMSOL® 软件中实现。不熟悉该主题的读者可以先阅读该系列文章,获得一些理解。本节,我们从今天的示例中总结了所需的主要思想。
拉格朗日乘子法用于将约束的变分问题转变为等效的无约束问题。考虑约束变分问题
(1)
(2)
该约束问题的可行临界点是增广泛函的驻点
(3)
{\prime})dx+\int_a^b\lambda(x)g(x,u,u^{\prime}
)dx.
取这个泛函的变分导数
(4)
\delta E = \delta \int_a^b F(x,u,u^
{\prime})dx+\delta \int_a^b\lambda(x)g(x,u,u^{\prime}
)dx.
假设问题不受约束的部分已经得到处理,我们只想添加必需的强制约束。那么我们的关注对象就只是上述方程中的第二项部分。在 COMSOL Multiphysics 中,当添加一个物理场接口时,可以将其视为添加无约束的变分问题。之后,可以通过一个或多个内置标准边界条件添加对边界和域的约束。如果我们有一个软件未内置的非标准约束怎么办?我们可以使用弱贡献灵活地添加此类条件。
回到上面的函数,让我们关注来自约束的贡献。
\delta E = \framebox
{其他项}+\delta \int_a^b\lambda(x)g(x,u,u^{\prime})dx = \framebox{其他项}
+ \int_a^b\left[\lambda \delta g+g\delta \lambda\right]dx .
对于上述的分布式约束,拉格朗日乘数 \lambda (x) 是一个在受约束的几何实体上定义的函数。另一方面,对于全局约束,例如积分或平均约束之类,拉格朗日乘数是一个数字。假设我们要施加全局积分约束
\int_a^bg(x,u,u^
{\prime})dx-G = 0.
增广泛函是
它的变体是
)dx + \delta \lambda\left[\int_a^bg(x,u,u’)dx – G\right] ,
(5)
\delta E=\framebox
{其他项} + \lambda\int_a^b\left[\frac{\partial g}{\partial u}\delta u + \frac{\partial g}{\partial u’}\delta u’\right]dx + \delta \lambda\left[\int_a^bg(x,u,u’)dx – G\right].
因此,如果您想要对解强制执行的边界条件或其他约束不是内置的,但有一个内置的物理场接口,您需要做的就是使用 弱贡献 节点在上述方程中添加最后两项。下面,我们用一个例子来演示。
约束弹簧的平均垂直位移
在这个示例中,一个弹簧被刚性固定在底端,我们希望顶端(下图中的边界 4)有 2 cm 的平均垂直位移。这是一个线性弹性问题,这个物理场是内置的。此外,刚性固定一个面是一个标准的边界条件。另一方面,没有指定面的平均位移。
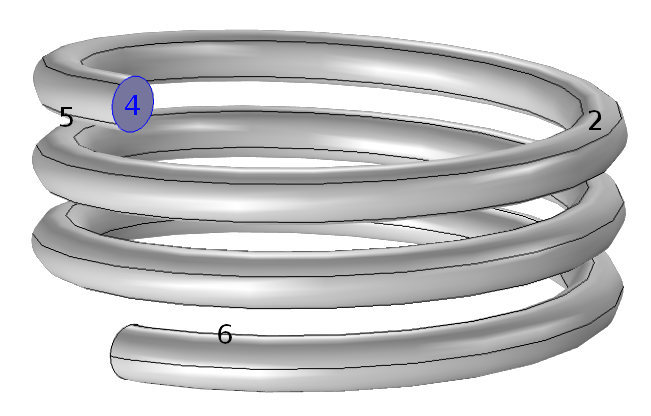
请注意,我们并不是要求面上每个点的垂直位移为 2 cm。这可以使用软件内置的指定位移 节点来指定。全局约束
(6)
其中,A 是有问题问题中的面,dh 是所需的平均垂直位移(在我们的例子中为 2 cm)。这里,dh 不是任何量的微分。它只是面上的平均垂直位移的参数名称。我们可以直接写为 2 cm。
除了使用标准特征实现这个约束之外,这个变分问题就变成了寻找增广泛函的驻点
+ \lambda\left[\frac{1}{A}\int_A wdA – dh\right].
对应的稳态条件是
(7)
\int_A wdA – dh\right] = 0, \quad \forall \quad \delta u, \delta v, \delta w, \delta \lambda.
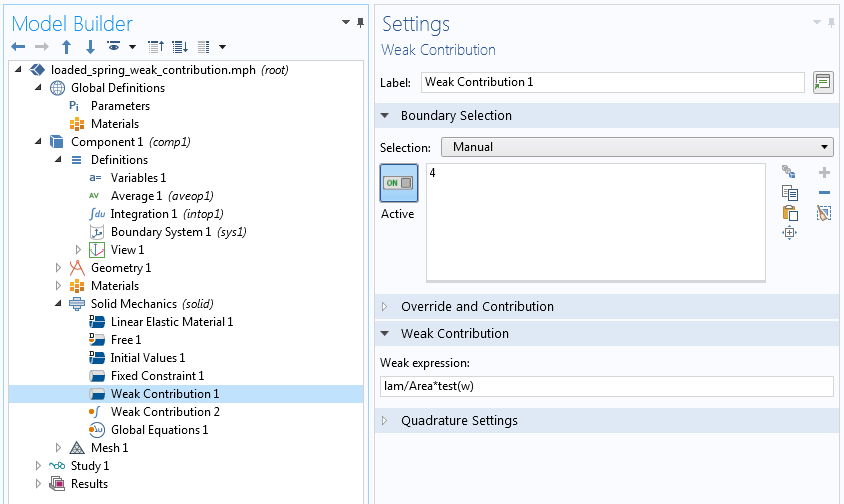
我们使用边界弱贡献和全局弱贡献来添加这两个贡献。在模型开发器中,我们可以通过图标区分边界和全局弱贡献。边界贡献与边界条件具有相同的图标,而全局贡献的图标有一个积分符号(\int)。此外,边界贡献的设置窗口包含一个边界选择部分,而全局贡献没有几何实体选择。
对面上的平均位移施加约束边界和全局弱贡献。
最后,变量 \lambda 是我们在拉格朗日乘法中定义的辅助全局变量。任何与约束相关的新变量都必须根据约束的性质在弱贡献节点的辅助变量 子节点或全局方程 节点中定义。
在我们的示例中,有一个全局约束,因此,我们必须使用全局方程 节点来定义它。通常,在全局方程 设置窗口中也会输入一个方程。这里没有必要,因为我们在弱贡献中包含了一个包含拉格朗日乘数变化的项。稍后将讨论另一种选择——使用全局方程 节点来定义全局自由度及其方程。全局方程为我们的问题增加了一个自由度。
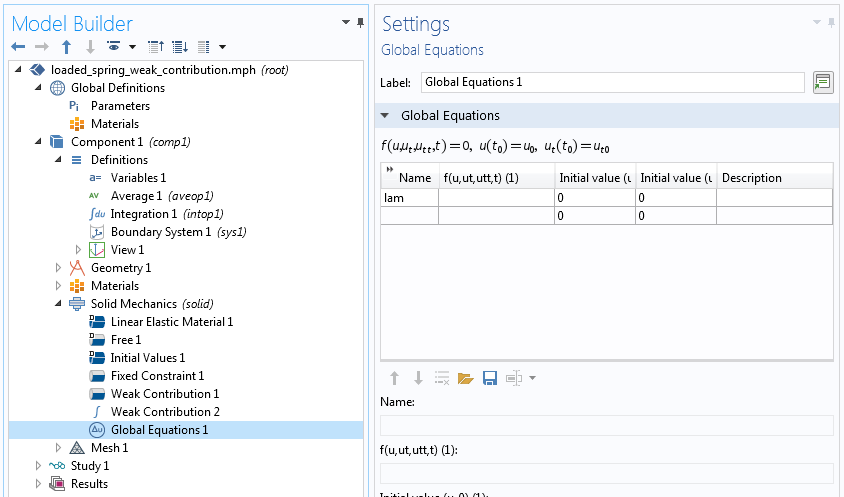
定义一个辅助全局未知数。
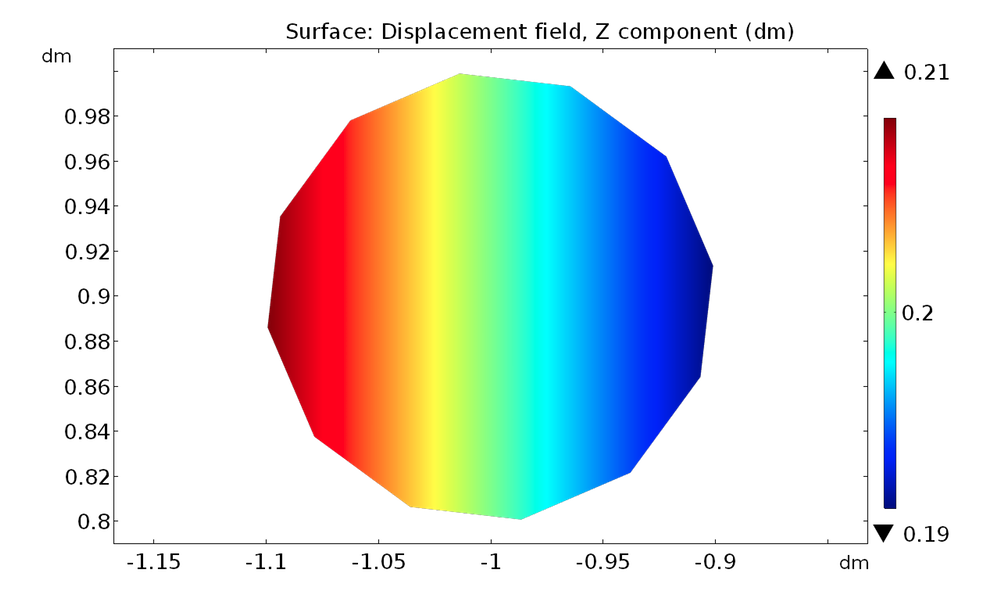
如果求解这个问题,我们会得到如下所示的解。我们可以在结果 > 派生值中看到拉格朗日乘数和平均位移。如果我们查看约束面上的垂直位移,可以发现它是不均匀的;它只是根据约束的要求平均为 2 cm。
关于上述实施的两个项目,我们想澄清两点:
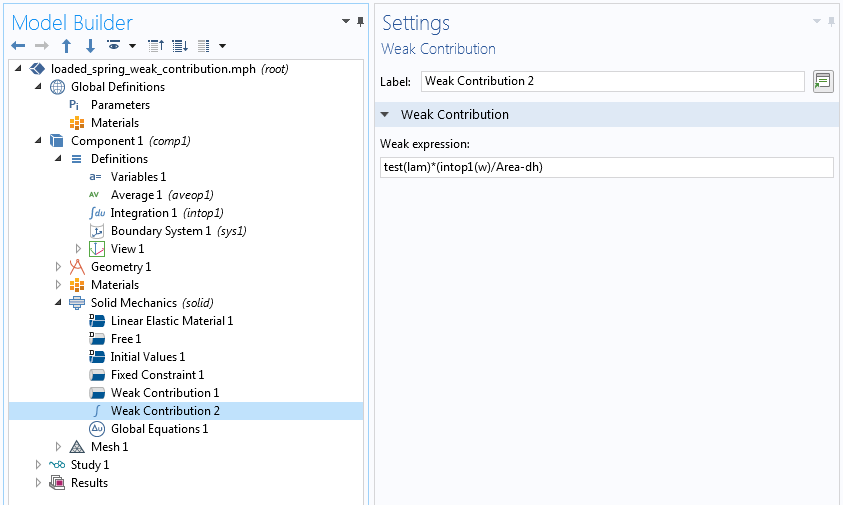
- (方程.7)中的第二项和第三项都包含积分。在边界弱贡献,弱贡献 1)中,我们只添加了被积函数。另一方面,全局弱贡献中的积分需要显式调用积分算子。或者,我们可以将被积函数
test(lam)*w/Area添加到弱贡献1 并在弱贡献2 中仅保留-test(lam)*dh。 - 这个示例中的约束是全局的。对于一个分布约束,拉格朗日乘数是一个位置函数,必须被定义为边界弱贡献下的辅助变量。有关这种区别的更多信息,请参阅我们关于变分约束的博客文章。
替代实现方法
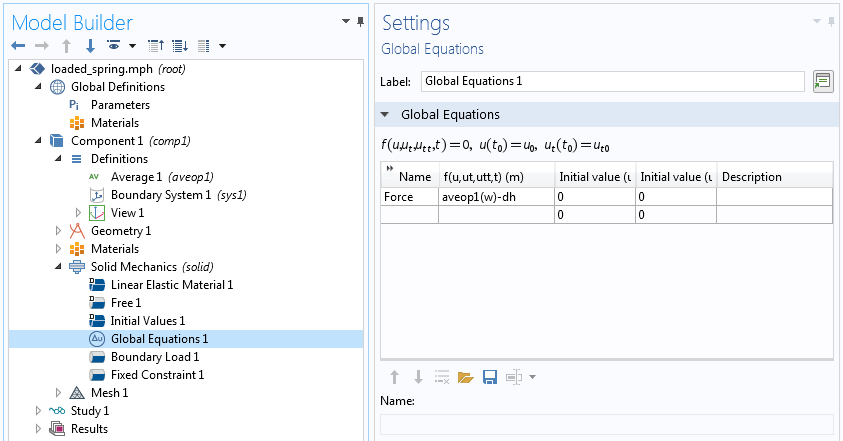
乘以拉格朗日乘数的变化项 \delta \lambda,可以在全局方程 节点中指定,该节点中定义了拉格朗日乘子。下面的屏幕截图显示了如何执行此操作。仅替换了(方程7)中的第三项。该项不包含\delta \lambda,仍然必须指定为边界弱贡献。请注意,intop1() 是定义在边界 4 上的积分算子,Area 是由 intop1(1) 给出的边界的面积。
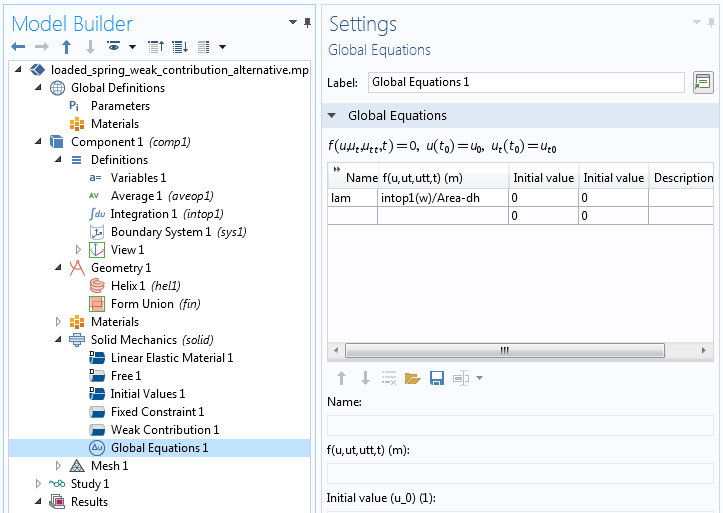
包含全局拉格朗日乘数变化的弱项的替代说明。
拉格朗日乘数的物理解释
上述解决方案为我们提供了由移动边界 4 引起的位移和应力,平均垂直位移 2 cm。问题是:我们如何在物理上强制结构符合我们的愿望?你猜对了。我们施加了一个力。拉格朗日乘数与强制执行约束所需的力(通量)有关。这里的关键词是相关 的。接下来,让我们详细了解它的含义。首先,让我们尝试约束的另一种表达式。
(方程6) 中的约束在数学上等效于
(8)
对应于这种形式的约束的增广泛函是
\framebox
{其他项} + \lambda\left[\int_A wdA – Adh\right],
对应的稳态条件是
(9)
+ \lambda\left[\int_A \delta wdA\right] + \delta \lambda\left[\int_A wdA – Adh\right] = 0, \quad \forall \quad \delta u, \delta v, \delta w, \delta \lambda.
如果我们把这个方程中的最后两项作为弱贡献并求解,会得到一个拉格朗日乘数,这与我们在第一个操作中获得的结果大不相同。尽管如此,位移和应力仍是相同的。因此,我们可以怀疑,拉格朗日乘数本身并不是一个物理量,因此它不能告诉我们如何在物理上执行所需的约束。要找出我们应该在物理上做什么的一种可靠方法是,对结果进行后处理并查看反作用力(通量)。
为了严格确定拉格朗日乘数在物理上是什么,我们必须查看一下迄今为止一直隐藏的方程的无约束部分。在今天的这个例子中,就是查看固体力学方程的弱形式。对于处于平衡状态的可变形固体的弱形式,也称为虚功方程,由下式给出
(10)
-\int_V\sigma:\delta \varepsilon dV +\int_V\mathbf
{b}\cdot\delta\mathbf{u} dV+\int_A\mathbf{\Gamma}\cdot\delta\mathbf{u}dA =0 \quad \forall \delta\mathbf{u},
式中,\mathbf{u} = (u,v,w) 是位移矢量和\sigma, \varepsilon, \mathbf{b}, 和 \mathbf{\Gamma} 分别是应力、应变、单位体积的体载荷和边界载荷。启用方程视图 可以查看任何 COMSOL Multiphysics 物理场接口的弱形式。
如果我们将(方程 10)、(方程 9) 和 (方程 7) 进行比较,会看到今天示例中的拉格朗日乘子与约束面上的边界载荷出现在同一位置。一个区别是拉格朗日乘数出现在表面积分外,而边界载荷在积分内部。这源于我们约束的全局性。另一个区别是我们示例中的拉格朗日乘数与垂直位移 w 一起出现,而固体力学方程中的表面载荷是点乘以位移矢量的变化量。让我们逐一地来协调这些项目。
\cdot\delta\mathbf{u}dA = \int_A\left[\Gamma_x\delta u + \Gamma_y\delta v + \Gamma_z\delta w\right]dA.
现在,我们看到拉格朗日乘数与边界载荷的垂直分量有关。最后,如果边界载荷是恒定的,有
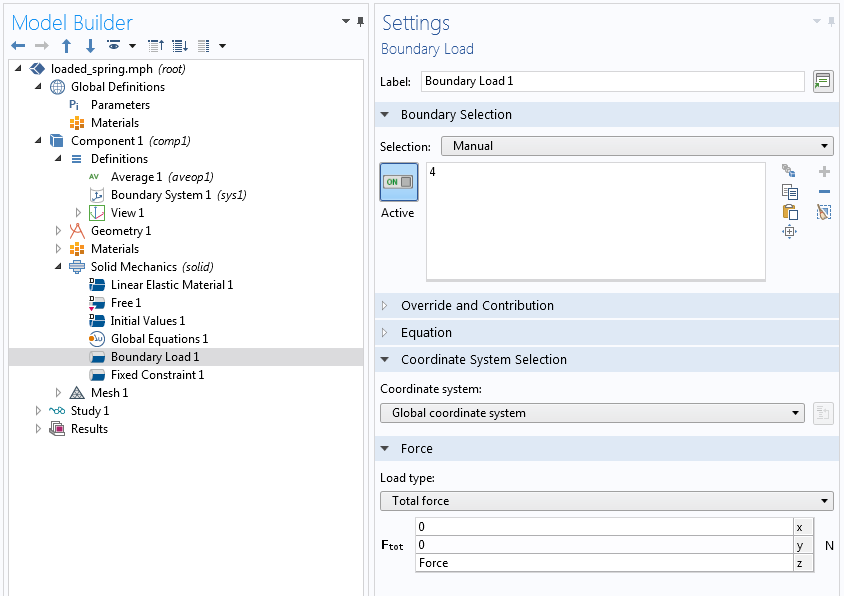
将其与(方程7)进行比较,可以看到在我们的第一个操作中,拉格朗日乘数对应于总垂直边界载荷。现在我们知道对于特定物理场和特定形式的约束方程,拉格朗日乘数是面上的总垂直载荷,我们可以使用内置的边界载荷 节点来强制约束而不是弱贡献。这一过程可以在 COMSOL 案例库中负载弹簧案例教程中详细查看。
当我们知道拉格朗日乘数的对应物理意义的替代实现方案。
最后一个实现可以看作是要求软件施加所需的任何垂直总力来强制平均垂直位移。我们可以这样做,是因为通过查看固体力学方程的弱形式,我们确定了拉格朗日乘数和总力之间的对应关系。我们并不总是可以用标准力(通量)项建立这种联系。请注意,我们可以使用默认的分布式边界载荷,这只会改变内部使用的额外自由度的数量。
一般来说,对于维度一致性,在(方程3)中,拉格朗日乘数与约束的乘积 g 应该给出每单位体积、面积或长度“能量” E 的密度,这取决于约束所应用的几何实体。在许多工程问题中,E 字面上代表能量,因此,我们说拉格朗日乘数与约束在能量上共轭。这意味着,例如如果我们缩放、平方或进行任何数学上改变约束方程单位的操作,那么拉格朗日乘数的单位和物理意义就会改变。然而,\lambda \frac{\partial g}{\partial u} 是不变的,因为它总是与u(方程 5)能量共轭。拉格朗日乘数和雅可比约束的乘积在广义上是一个力(通量)密度。如果 \frac{\partial g} {\partial u}
=1,这通常是线性约束的情况,拉格朗日乘数确实是广义力(通量)。
弱贡献的美妙之处在于,您可以强制执行约束,而无需通过内置物理场的弱形式。您可以对结果进行后处理以找出实际的物理过程。该实现与物理场无关。
关于弱贡献的总结性思考
今天,我们讨论了 COMSOL Multiphysics 软件如何帮助非标准边界条件的实施。使用弱贡献,我们可以用一个灵活的且与物理场无关的策略来添加不常用到成为软件标准功能的约束。该方法的数学本质是求解某个量的最小极值问题,但这种思想可用于由没有相应变分解的偏微分方程给出的问题。有关此主题的更多背景知识,我们推荐您阅读关于弱形式和变分问题的系列博客。
下一步
如果您对弱贡献或其他主题有任何疑问,或者想详细了解 COMSOL Multiphysics 的特性和功能如何满足您的建模需求,欢迎您与我们联系。
查看以下 COMSOL 案例库中示例和博客文章,了解在各种物理领域中使用弱贡献和额外方程的更多演示:







评论 (8)
稳军 赵
2022-10-25很好,学习了
James Z
2023-01-31请问有分布式边界条件,如位移、速度和加速度分布的例子么?
hao huang
2023-02-06 COMSOL 员工您好,可以考虑直接使用固体力学物理场进行设置。如果一定要采用 PDE 形式建模,对于分布式边界可以考虑使用逐点约束或弱贡献进行添加。
译彬 王
2024-03-19请问comsol帮助文件中已经有的弱形式方程还需要自己设定吗
正清 韦
2023-04-21请问如何用弱贡献实现floquet周期性边界条件呢?在模拟磁子晶体遇到了困难
Qihang Lin
2023-04-25 COMSOL 员工这部分如果自定义建模则需要您自己查阅相关公式后自己推导公式,软件内置的磁场接口则已经内置周期性边界功能。
Yichen Li
2025-03-13comsol边界条件设置弱贡献为什么不会显示”已代替”默认的边界条件(如零通量边界),难道说弱贡献会默认抵消原有的边界条件?
Jun Leng
2025-03-14 COMSOL 员工弱贡献和默认边界条件是相互补充的关系,它们共同作用于模型的求解,因此在设置弱贡献时不会显示 “已代替” 默认边界条件。