最新内容
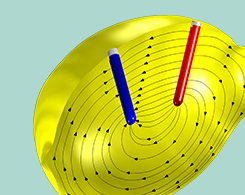
如何建立电化学模型——以柠檬电池为例
2020年 5月 5日
在本篇博客文章中,我们将讨论如何从头开始建立电化学和电池模型的一般过程,并以柠檬电池为示例来演示建模过程。

如何创建包含 CAD 导入和选择的仿真 App
2020年 4月 30日
在使用 COMSOL 软件二次开发的过程中,你可能会遇到这样的问题:如何使用 App 开发器创建可以处理 CAD 导入并能让用户交互式选择边界条件的仿真 App?我需要了解编程吗?

通过仿真优化多工件电镀工艺
2020年 4月 28日
从日常的厨房用具到标志性的颁奖礼小雕像,架子电镀是一个有用的制造过程,确保组件电镀都统一和有效。
仿真助力环境保护的 6 种行业应用
2020年 4月 22日
节能建筑和电器,安全的核废料储存,保存完好的淡水湖泊。 这些都是模拟如何保护环境的几个例子。

Wi-Fi 天线附近人体头部的比吸收率测量
2020年 4月 16日
如今,人们经常暴露在手机(或其他无线设备)等移动电子设备的射频(RF)辐射中。人体吸收的射频暴露量用比吸收率(SAR)来衡量,比吸收率代表射频能率。
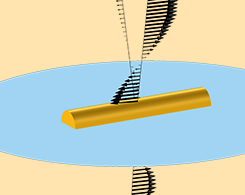
模拟物体在基板上的光散射
2020年 4月 14日
电磁波中的一个常见建模场景:计算光在均匀介电基板顶部图案化的结构上的散射。
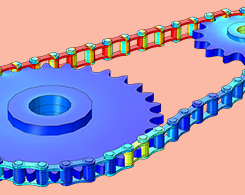
如何在 COMSOL Multiphysics® 中模拟链传动系统
2020年 4月 9日
在之前的博客文章中,我们讨论了如何使用 COMSOL Multiphysics® 零件库中的内置参数化几何零件,轻松创建滚子链轮组件的几何模型。
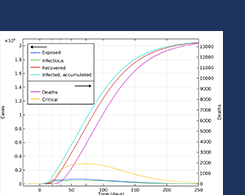
使用 COMSOL Multiphysics® 模拟 COVID-19 的传播
2020年 4月 7日
从易感者,暴露者,感染者到恢复者:了解数值模型如何帮助我们了解COVID-19大流行的动态及其传播方式。



