最新内容

光声光谱腔拓扑优化分析
2019年 5月 24日
在气体光声光谱学中,光和声用于检测周围环境中有害化合物的浓度。与其他光谱技术相比,光声学由于其检测方案而显示出最高的信噪比——但由于产生的声波通常太弱而不能被麦克风检测到,因此我们使用声学单元来放大信号。
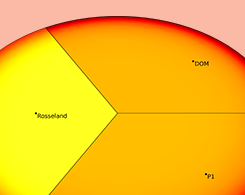
参与介质中辐射传热的 4 种计算方法
2019年 5月 22日
离散坐标法,P1 近似,Rosseland 近似,或者比尔-朗伯定律:你应该用哪一个来分析参与介质的传热?
仿真助力设计药物输送系统
2019年 5月 17日
你有没有紧张过,感觉就像被一个小小的闪电击中一样?但是值得庆幸的是,这种疼痛通常会在几天之内消失。不过,遭受严重伤害的人并不是那么幸运,这种痛苦可能会持续数月之久。
使用 COMSOL® 软件仿真锂离子电池中的电极平衡
2019年 5月 16日
如果锂离子电池的电极平衡不正确,则电池开路电压将不会准确。在本篇博客文章中,我们将介绍电极中的物质守衡以及其是如何产生的,并使用 COMSOL Multiphysics® 软件演示了一个简易电池模型。

评估轴承不对中对转子振动的影响
2019年 5月 14日
从 MEMS、涡轮机到电动机,甚至船舶,各种设备中都有轴承。我们如何解释轴承的不对中(以及由此产生的转子振动)取决于其用途。
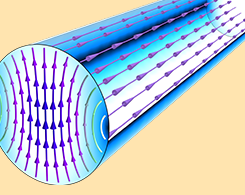
如何在 RF 模块中使用圆形端口
2019年 5月 10日
RF 模块中的 端口 边界条件是 COMSOL Multiphysics® 软件的附加功能,可用于发射和吸收电磁能。在本篇博客中,我们将介绍如何设置一个圆形波导端口,并检查定义端口模场的解析解。
熵捕获中的 DNA 快速分离过程模拟
2019年 5月 9日
在调查犯罪时,法医专家有时会使用DNA证据来识别犯罪嫌疑人。然而,DNA不仅包含识别信息,还有我们基因构成的线索。DNA 分离可以用来深入研究 DNA 链,但是传统方法很耗时。

参与介质中的辐射传热和离散坐标法
2019年 5月 8日
这里一份关于离散纵坐标法,正交集,以及如何模拟辐射和参与或吸收介质之间的相互作用的完整指南。



