最新内容
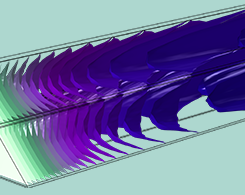
模拟多孔介质和活性颗粒床中的表面反应
在之前的博客文章中,我们讨论了表面在化学反应器中的特殊性。在本篇博客文章中,我们将讨论如何将反应器结构(如颗粒床)的表面积最大化,以及在固定床反应器具有局部几何复杂性且微观扩散很重要的前提下,我们如何简单而准确地进行模拟。
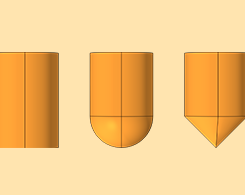
用 COMSOL Multiphysics® 分析开尔文探针设计
开尔文探针提供了一种无损、无触点的方法来测量各种材料组合的功函数差。这些探针可具有多种设计,包括不同的尖端形状、长度和半径。为了确定最佳设计,同时最大限度地减少测试,研究人员使用 COMSOL Multiphysics® 软件做了相关研究……

评估壳厚度对消声器性能的影响
来自 Lightness by Design 公司的客座博主 Linus Fagerberg 将继续上一篇博客文章的话题,讨论辐射声音与消声器壳厚度的关系。 在本文中,我们将讨论用于测量消声器性能的各种实体。其中一个很重要的参数是消声器壳厚度,我们将研究该参数对消声器性能的影响。通过执行声-结构相互作用仿真,我们能够看到壳厚度如何影响消声器的性能。
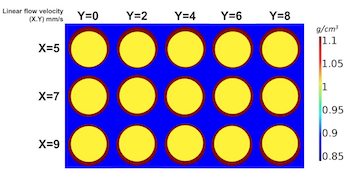
利用液滴微流控技术改进惯性聚变能靶制备工艺
人们经常会开玩笑说:核聚变能源将在30年后出现,而且永远如此。研究人员正在利用放着呢技术解决惯性聚变能靶制备所面临的挑战。

使用子模型计算多孔介质中的孔隙率和渗透率
多孔材料具有复杂的几何形状,因此可能难以建模。 建立微尺度子模型是寻找介质孔隙度和渗透率的有用方法。

通过仿真分析磁力开关的电动力学
磁力开关是一种重型断路器,可防止在高压情况下出现问题。参见一个用模拟研究他们设计的例子。

硅光子学:硅波导的设计和原型制作
1870 年,人们观看了一场水桶表演,舞台上的两个水桶一上一下套在一起。上面的桶开了一个小孔,水可以从中流入下面的桶中,并在这个过程中发生弯曲。令观众惊讶的是,太阳光也随着水一起发生弯曲——这种现象后来被称为“全内反射”。舞台上的表演者是约翰·丁达尔,他是尝试控制光这种最明显能量形式的众多科学家之一。

研究相变材料的热性能
在炎热的气候下,使建筑物保持均匀的温度是很耗费能源的。研究人员研究了相变材料作为一种解决方案的有效性。



