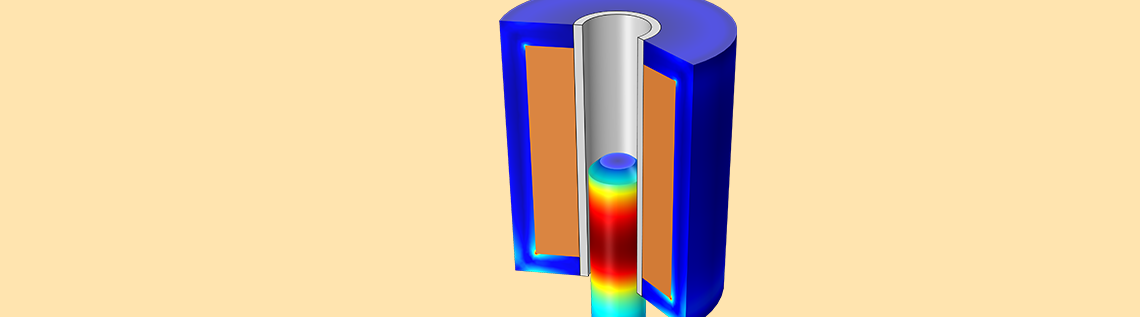
电磁柱塞是一种可将电能转换为线性机械运动的机电装置,它产生的机械运动可用于移动外部载荷,例如关闭电磁阀、关闭/打开电磁继电器等。电磁柱塞由多匝线圈、磁芯、非磁导向机构和磁性柱塞构成,在本篇博客文章中,我们将为您介绍如何模拟电磁柱塞的性能表现和动力学特征。
电磁执行器的广泛工业应用
部分工业应用离不开线性运动,线性电磁执行器在其中起到了不可或缺的作用,其用途包括打开或关闭、推动或拉动载荷等,常见的应用装置包括电磁继电器、电磁阀、断路器及接触器。此外,农业、建筑业、汽车工业和机器人产业中也常能看到此项技术。

一个由机械弹簧、线圈、电枢及磁轭构成的简易电磁继电器。
借助 COMSOL Multiphysics 的仿真功能,我们能够将线性电磁执行器的多项性能(例如驱动力和冲程、载荷曲线、效率和工作频率)作为尺寸、材料、输入电压和电流等设计参数的函数,并对其进行评估。在下文中,我们将通过一个案例来探讨具体的操作方式。
在 COMSOL Multiphysics 中模拟线性电磁柱塞
在本篇博客文章中,我们选用了一个由多匝线圈、磁芯、非磁导向机构及磁性柱塞构成的简易电磁柱塞。如下图所示,这些零件固定在弹簧和阻尼器上。瞬态(方波脉冲)电流经过螺线管线圈,在磁芯和柱塞周围形成了磁场。此磁场在磁芯和柱塞之间产生了吸引力,使柱塞加速并背向弹簧向上运动。当吸引力达到最大时,柱塞完全置于磁芯之中,此时形成了最低磁阻的磁通量路径。
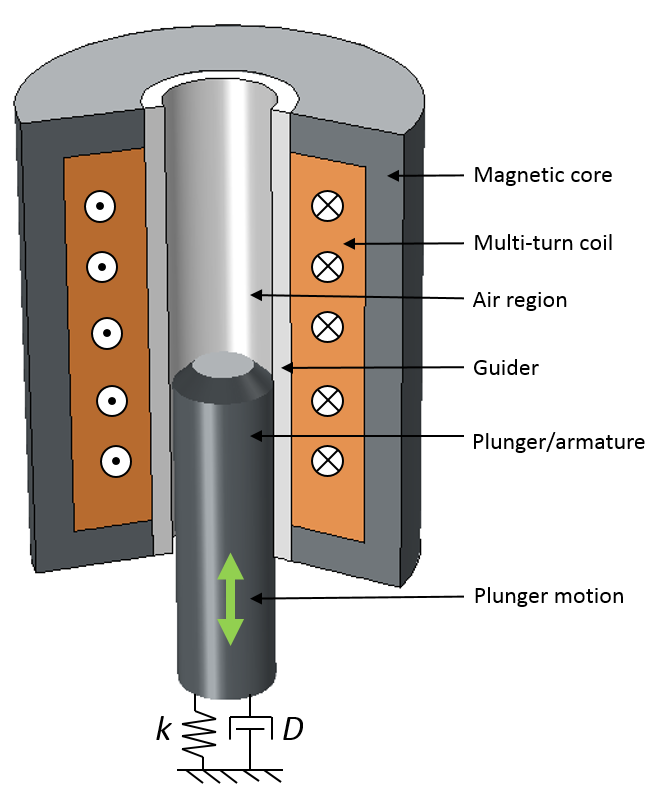
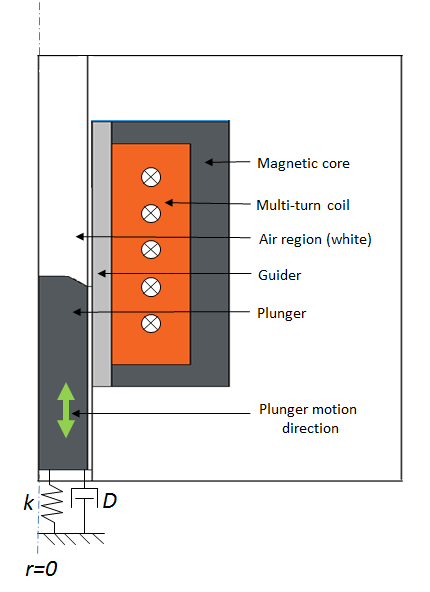
电磁柱塞的三维截面图(左)和二维轴对称图(右)。
我们在电磁柱塞教学模型中使用了一个二维轴对称几何几何,并添加了磁场,移动网格 接口、全局常微分和微分代数方程 接口以及瞬态 研究。接着,我们在全局定义 > 参数 中定义了模型参数,如下方的屏幕截图所示。
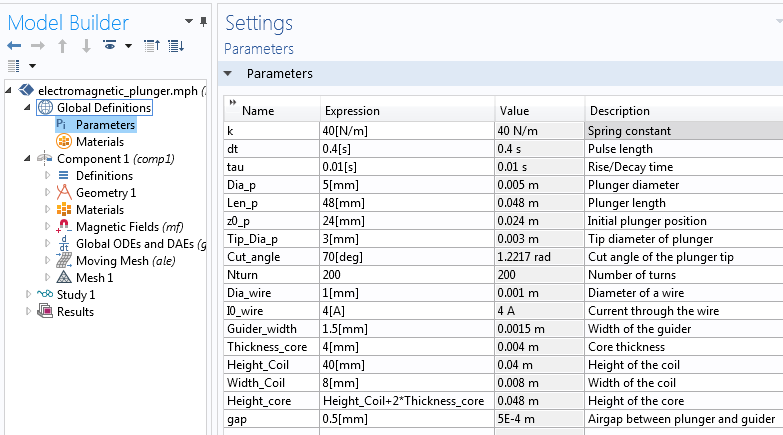
电磁柱塞模型的设计参数列表。
由于柱塞会进行大幅度的平移运动,因此我们需要使用滑动网格对其进行模拟。首先,为静态部件和移动部件分别创建一个单独的并集。然后,执行“形成装配”操作以定型几何,确保在界面自动创建“一致对”。为了更方便地进行建模,还可以为导向机构、磁芯、线圈、柱塞、源边界、目标边界和计算力边界创建多个选择,如下图中的彩色方框所示。
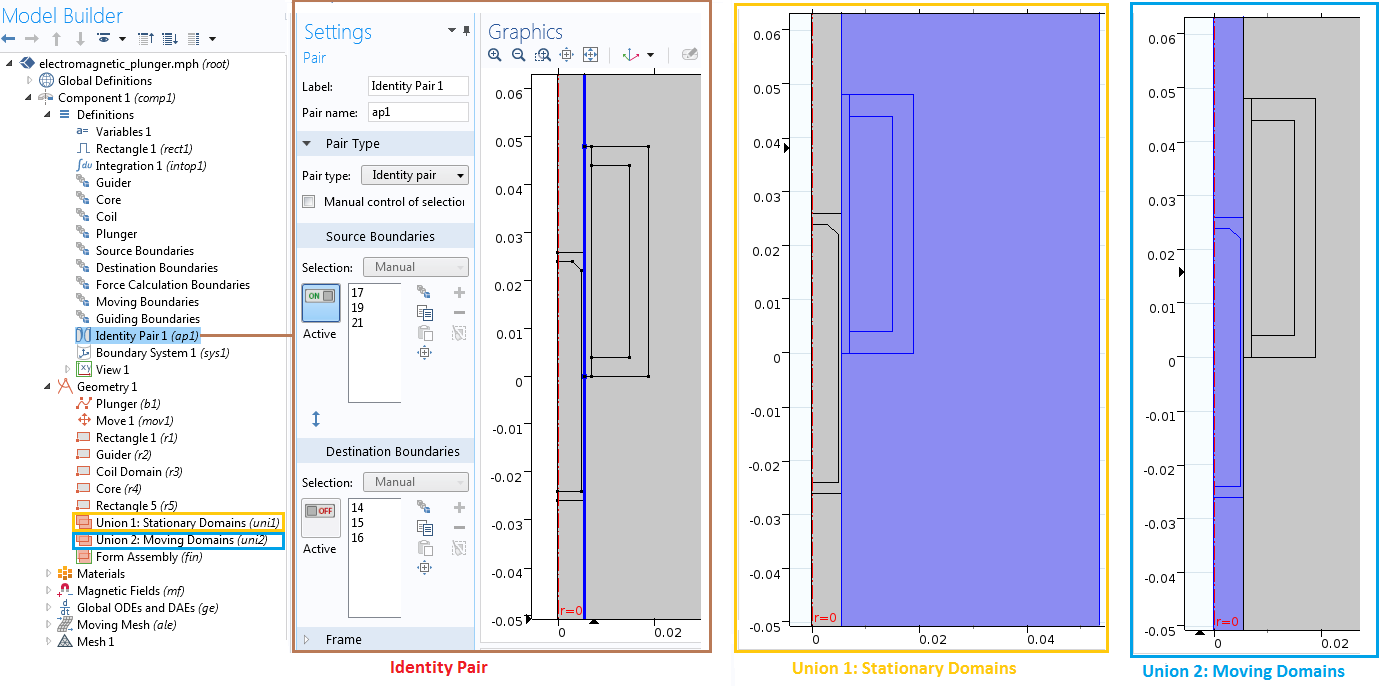
“模型开发器”中静态域、移动域和一致对选项。
执行动态研究需要计算出柱塞质量 M,故我们定义了一个积分算子 Integration 1 (intop1),用于计算柱塞的体积,并将它与指定的材料密度相乘。在本案例中,我们将柱塞的材料设为 Low Carbon Steel 1002(mat 3),即低碳钢。此外,我们还定义了电磁力的变量 F_z,并通过它来计算柱塞的 Maxwell 应力张量。记住,在执行计算之前,首先需要将计算力 功能添加到力名称为 force 的磁场 接口中。我们将在下一节中介绍具体的操作步骤。
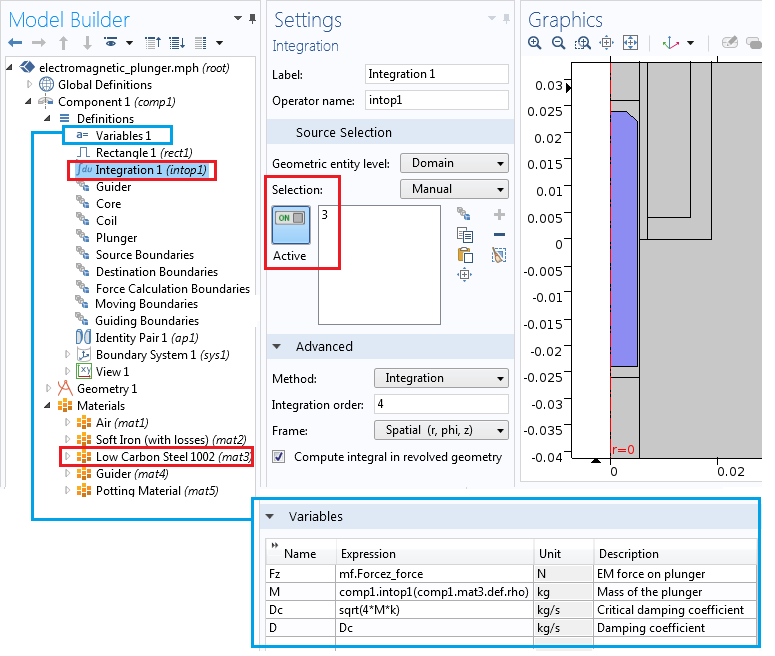
积分耦合算子与变量。
模拟电磁场
磁场 接口可用于模拟设备中的电磁场。首先,我们使用安培定律 节点来模拟构成柱塞和磁芯的非线性材料,并将两个节点的“本构关系”都设为“H-B 曲线”。通过相似的方式,我们在“软铁”制成的磁芯区域添加了非线性 H-B 曲线。请注意,虽然我们可以使用同一个安培定律 节点来模拟柱塞和磁芯,但是使用两个单独的安培定律 节点会让我们可以更加方便地根据具体需求采用不同的本构关系。
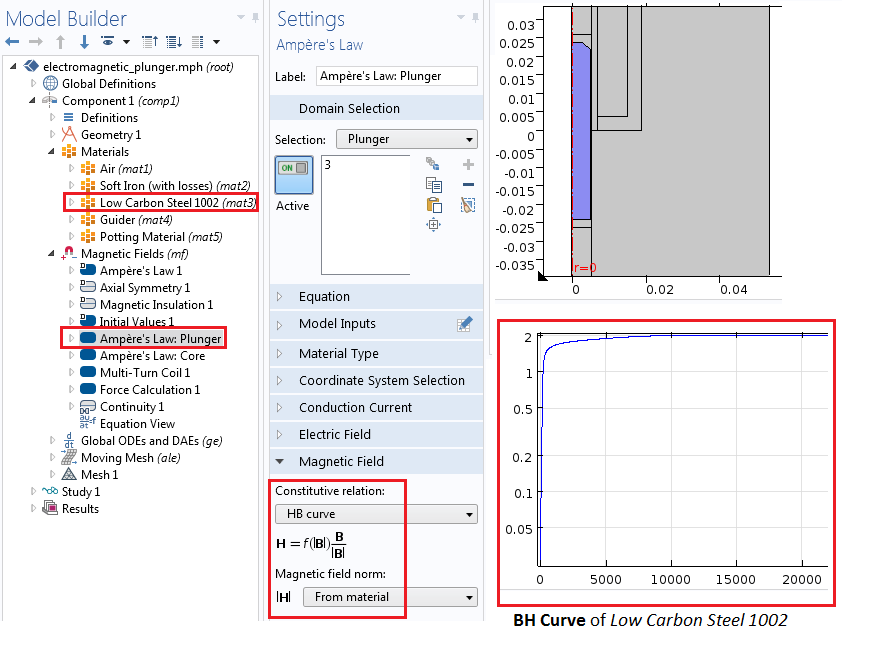
安培定律节点的设置,图象显示了在非线性磁性柱塞区域中应用 H-B 曲线。
接下来,借助磁场 接口中的多匝线圈 功能,我们可以创建螺线管绕组,它是由200 匝 (Nturns = 200) 直径为 1 mm (Dia_wire = 1 mm)、电导率为 6e7 s/m 的线圈构成。通过线圈的电流是被定义为 I_coil = I0_wire*rect1(t[1/s]) 的方波脉冲,其中 rect1() 是定义 > 方波 1 节点中定义的方波函数,最大电流为 I0_wire = 4 A。
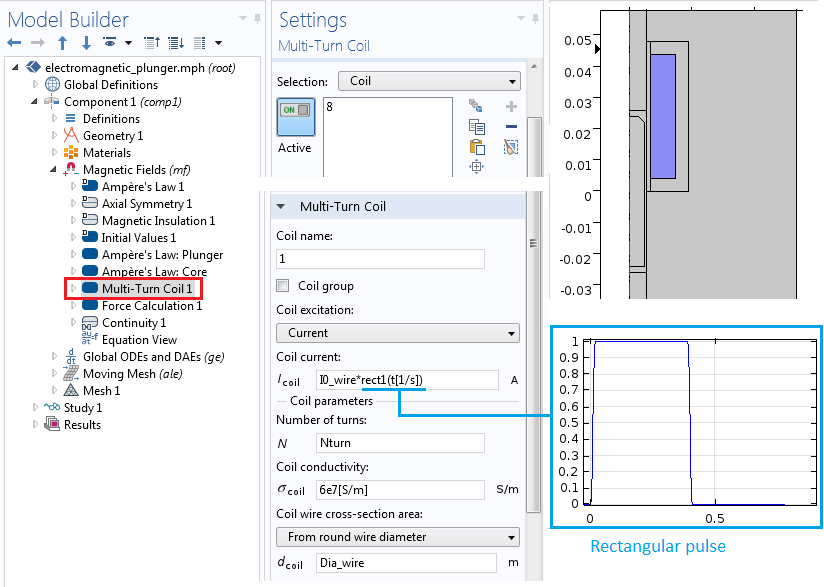
“多匝线圈”特征包含了开路、匝数、电导率及横截面积等内容的设置。
接下来,通过将“计算力”特征添加到柱塞域对柱塞的电磁力进行计算,计算结果包括柱塞上由于内部瞬态电流引起的 Maxwell 应力张量。由于柱塞是磁性材料,而 Lorentz 力仅支持导电非磁性材料,因此我们不能使用计算 Lorentz 力的方法。此外,Maxwell 应力张量方法对网格非常敏感,它要求添加了“计算力”功能的表面的网格剖分更加精细。为了获得更精准的计算力,您可以执行网格细化研究。
接下来,我们将在“一致对”物理场中添加“连续性”边界条件,以便耦合固定域和移动域之间的磁场。
添加全局常微分和微分代数方程
借助 COMSOL Multiphysics 的全局常微分和微分代数方程 接口,我们可以对电磁柱塞的刚体动力学进行模拟。固定在弹簧(弹簧常数为k)和阻尼器(阻尼系数为 D)上的电磁柱塞的运动方程如下:
(1)
{d^2p} {dt^2}
+D\frac
{dp}{dt}+kp-F_z(p,v,t)=0
其中,p 表示柱塞在 z 方向上的位置,v 表示速度,M 表示柱塞质量,F_z(p,v,t) 表示抵抗弹簧的电磁力。
上述方程可改写成两个独立的微分方程,分别描述柱塞的位置和速度:
(2)
以及
(3)
-v=0
我们可以使用全局常微分和微分代数方程 接口求解上述方程,并添加两个单独的全局方程,如下所示。
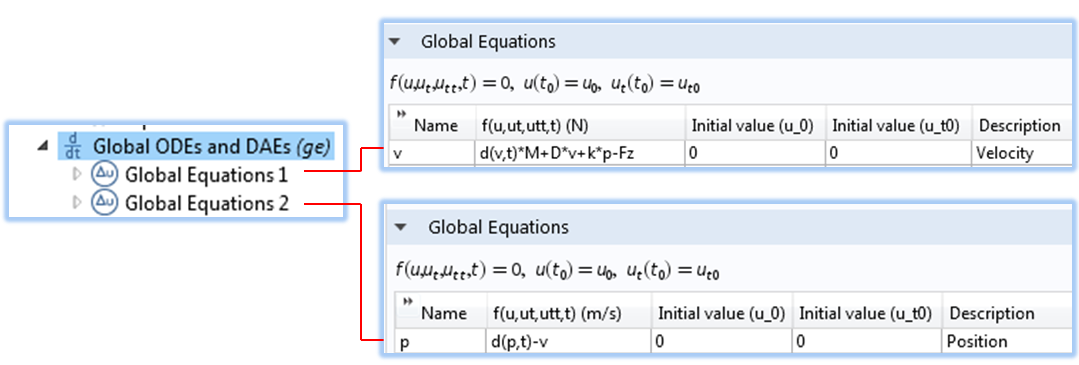
使用 全局常微分和微分代数方程接口指定用于描述速度和位置的微分方程组。
模拟平移运动
为了模拟电磁柱塞的平移运动,我们特意添加了移动网格 接口。与振动磁体教学模型中的建模技术相似,我们可以仅在移动域(柱塞和空气域位于一致对的左侧)内应用移动网格 接口。为了简化移动网格的设置,空气域被划分到了一致对的左侧。顶部和底部空气域的网格被设置成收缩或膨胀网格,中间空气域的固定网格则会根据指定边界位移的设置而移动。
为了彻底封闭柱塞,我们设置中间空气域的边界为指定网格位移 特征,并使特征中的变形等于位置变量 p。每一个变形空气域内的两条垂直边界(位于选择列表中“指导边界”下)仅在 r 方向上受到约束。下图显示了移动网格 接口的设置。
请注意:柱塞连同其周围的小型空气域都在移动。事实上,这有利于简化移动网格 接口的网格剖分设置,因为这一设置允许我们将网格映射到其他两个空气域。我们将在本系列博客的第二部分中处理更具挑战性的网格设置问题。
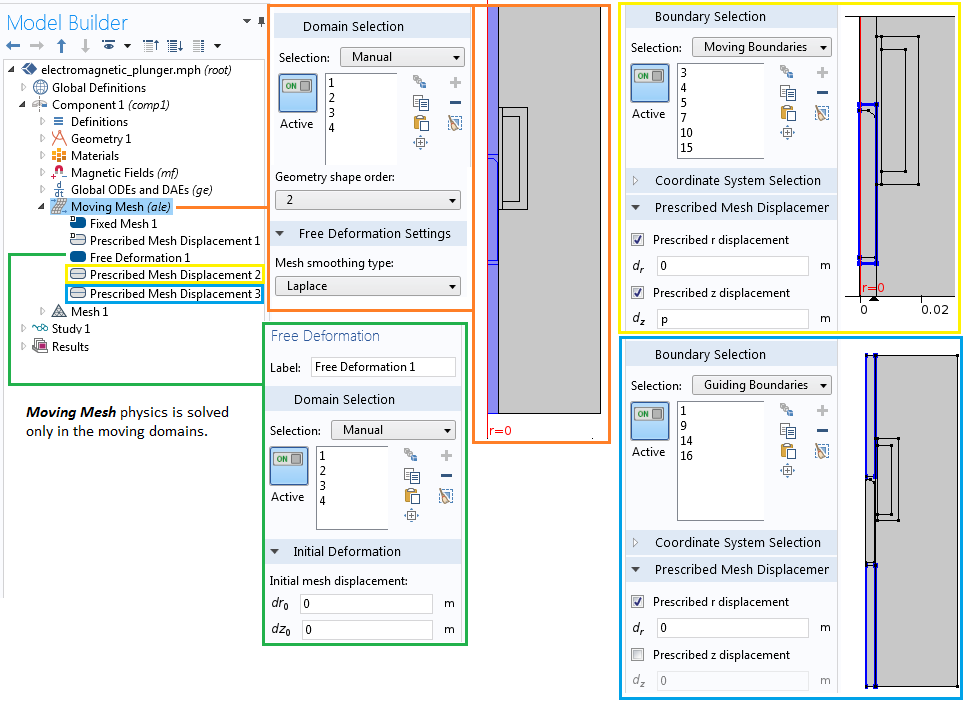
移动网格接口的设置窗口。
紧接着,我们向静态域指定了固定网格,并指定了移动组件在 z 方向上的变形。此外还使用了来自全局常微分和微分代数方程 接口的位置变量 p 对指定的运动进行了定义。
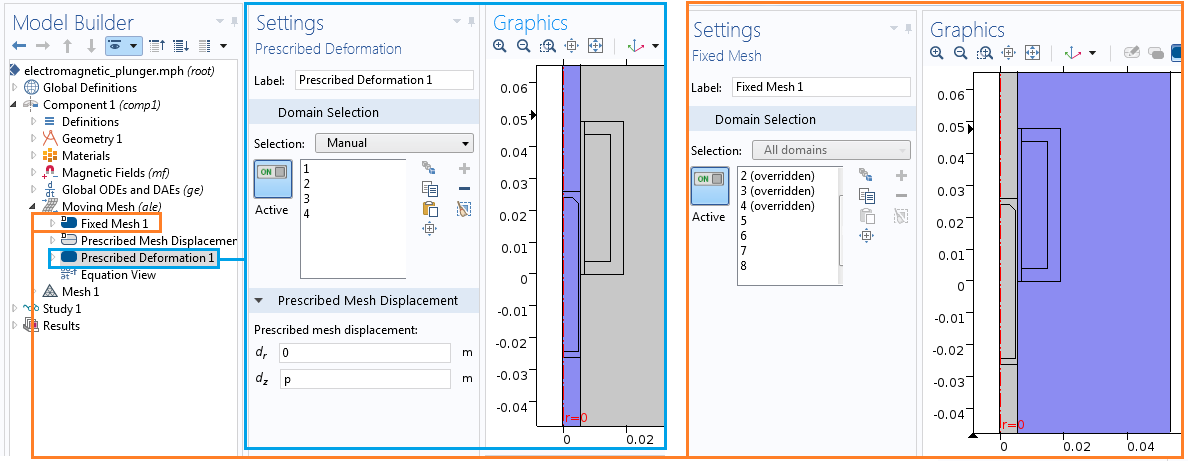
设置 移动网格接口的另一种方法。
评估仿真结果
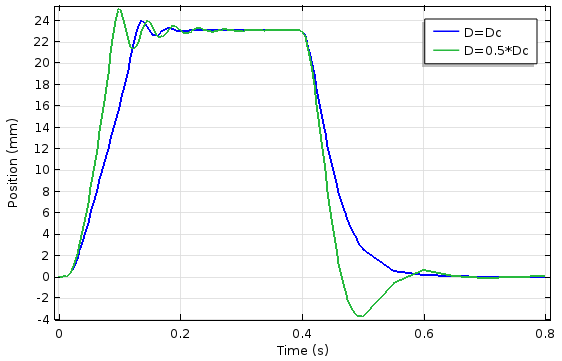
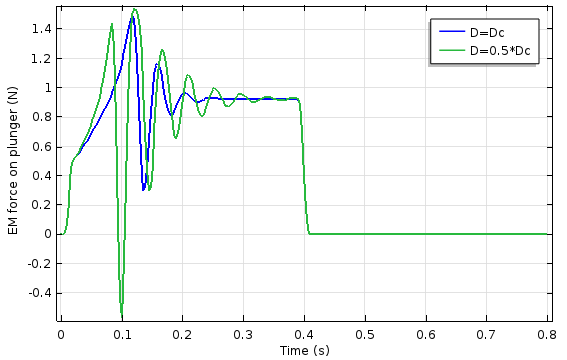
电磁柱塞的瞬态研究结果如下图所示。我们分别对两个不同的阻尼系数值运行了仿真。正如预期,当阻尼系数小于临界阻尼系数时,系统将表现出更强的振荡性,然而其过冲的上升时间也变得更短。
柱塞位置(左图)和柱塞承受的电磁力(右图)随阻尼系数和时间变化的曲线。
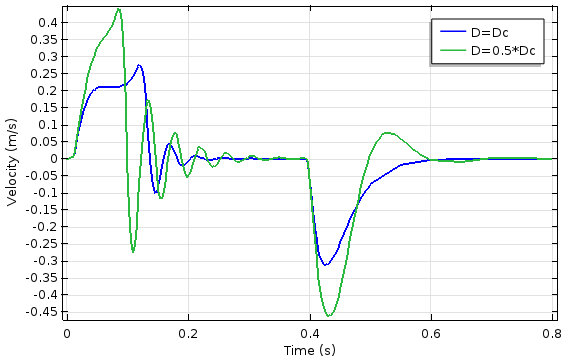
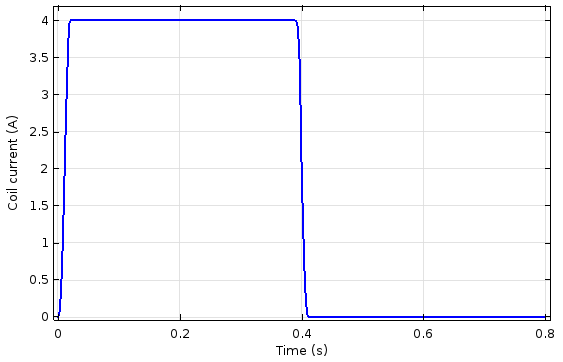
柱塞速度随阻尼系数和时间变化的曲线(左图),以及流经线圈的电流随时间变化的曲线(右图)。
下方动画演示了对线圈施加瞬态电流时,柱塞的动力学特征。左侧图像为电磁柱塞模型及其磁通密度的三维可视化绘图,右侧的两张绘图分别描述了柱塞的位置和通过螺线管线圈的电流。
关于模拟电磁柱塞和执行器的结语
在本篇博客文章中,我们介绍了如何使用三个不同的物理场接口对线性/平动电磁执行器进行建模,这三个接口分别是磁场,移动网格 接口和全局常微分和微分代数方程 接口。我们将磁场 接口与移动网格 接口及描述柱塞动力学的微分方程进行了充分的耦合,从而计算出了电磁力、柱塞位置以及柱塞速度。
随后我们还将发表另一篇博客文章,进一步介绍如何模拟振荡受限的柱塞的动力学特征,同时还将演示如何使用事件 接口来模拟电磁柱塞的接触和释放操作。敬请期待!



评论 (27)
聪 郑
2020-06-07请问能不能系统的说一说求解电磁力的具体方法有哪几种,适用情况各是什么情况?
Haili Wang
2020-06-11 COMSOL 员工郑聪,您好!
感谢您的留言。
电磁力计算主要包括三种方法,分别是:“洛伦兹力”,“Maxwell-应力张量”和“虚功原理”。
1) “洛伦兹力”用于有电流流过的时候,也是比较常用的一种方法,如果和“固体力学”耦合的话,直接在固体力学中添加“体载荷”然后在下拉菜单中选择“洛伦兹力贡献”即可。如果想要得到总力的话,可以在受力对象所在的域对“洛伦兹力”进行体积分即可。
2)如果利用“Maxwell-应力张量”法来计算的话,需要用空气域将受力对象包裹,同时在COMSOL中添加“计算力”域条件,Maxwell-应力张量计算得到的是总力,而且同时考虑“磁力”和“电力”。
3)虚功原理的计算原理是在力的方向上给一个微小几何位移,从而计算磁能/电场能的变化。关于虚功原理的计算方法,可以参考下述链接中的案例:
http://cn.comsol.com/model/electromagnetic-force-calculation-using-virtual-work-and-maxwell-stress-tensor-20681
祝好!
王海莉
COMSOL 中国
yangji zeng
2021-02-06请问一下,对于线圈的激励,可以使用电压激励吗?
hao huang
2021-02-24 COMSOL 员工您好,可以使用电压激励线圈。
Liwang Ai
2021-07-25您好,请问在模拟较大位移的直线运动时,移动网格中的自动对解重新划分网格,主要适用于什么情况?为什么自动重新划分网格后的,得出的力数据出现跳跃,不连续?期待您的回复。谢谢
Huangjun Xie
2022-01-02这个case中考虑了线圈的电磁感应么?就像“涡流制动器”和“动磁生电”的caes那样,与这个case中衔铁(armature)在线圈产生的磁场作用下运动时会改变线圈内的磁场,此时照理说应该会在线圈内激发一个感生电动式,从而使线圈电流出现一个陡降再上升的趋势,但是在这里却没有看到这个,是在这种情况下COMSOL的瞬态磁模块不能考虑感生电动势的影响么?
张 衍林
2024-03-14老师您好,我想请教一下我使用永磁体提供稳态的磁场,然后频域的50Hz交流电来计算电场,用着两部分给液态金属提供安培力,我看最终液态金属的流动速度从0增大趋于稳定。我想请问像我这种当磁场方向不改变,这个频域的交流电他在计算的时候有考虑电流方向的周期性变化么?因为电流的方向变化会导致液态金属手里的方向变化,请问我使用频域的交流电来计算是否合理呢?
没延 韩
2024-03-15 COMSOL 员工频域里会把直流量也变成频域物理量。所以这里建议使用“小信号分析”,即稳态(计算永磁体)+频域扰动(计算频域项),参考案例
https://cn.comsol.com/model/small-signal-analysis-of-an-inductor-2128;
https://cn.comsol.com/model/loudspeaker-driver-in-3d-8212-frequency-domain-analysis-92351;
后者是电声器件,考虑永磁体、铁芯、交变电流的线圈三者相互影响。
同时要注意,所谓“小信号分析”要求交流分量不能大于直流分量。
张 衍林
2024-03-16抱歉,您发送的网址点击进去并没有显示内容,请问这是怎样一回事呢?
“Sorry, the page you requested was not found
You may have selected an outdated link or may have typed the page address (URL) incorrectly.
You might find what you’re looking for by using the following search tool.”
没延 韩
2024-03-26 COMSOL 员工请将网址后面的标点符号删除。
张 衍林
2024-03-26请问有添加交流电电流终端的案例么?我看您推荐的这两个案例并不是添加电流的
张 衍林
2024-03-16请问有没有分析三维瞬态交流电的案例呢?我单纯对一个三维圆柱体施加交流电的时候会发生不收敛的情况,在最初的时候就会不收敛,
报错是“重复误差测试失败,可能已达到奇点。
时间:0。
最后一个时步不收敛。”
不知道是不是我的边界条件哪里设置的有问题。
没延 韩
2024-03-26 COMSOL 员工可参考案例库→AC/DC→设备,电感→E磁芯变压器。收敛性差可能是时间步长设置问题。
张 衍林
2024-03-26请问一下,添加瞬态的交流电终端的时候,正弦信号需要在最开始的时候添加一个斜坡函数来让信号添加平滑的时间么?我看到“扬声器驱动器 – 瞬态分析”这个案例里面是这样子说的。https://cn.comsol.com/model/loudspeaker-driver-in-3d-8212-frequency-domain-analysis-92351;
没延 韩
2024-04-25 COMSOL 员工这里是为了提高收敛性,如果初相为0,那么0时刻过零,所以sin函数加与不加斜坡函数均可。
张 衍林
2024-03-30我想请教一下如果说我使用永磁体提供给磁场,在用交流电提供电流,然后想计算从磁流体动力学,那我的交流电使用瞬态还是频域呢?用频域的交流电来计算安培力是否可以呢?
没延 韩
2024-04-25 COMSOL 员工如果使用频域,那么永磁体的磁场也变成了交变磁场,单纯的频域研究不会识别直流偏置。对这种交直流叠加的电磁场景,我们一般用两种方法,当直流偏置很大,交流信号很小时采用小信号分析的研究方法;当直流信号和交流信号大小相近或者交流信号很大时,采用瞬态。
程 王
2024-05-18如何改变电磁铁运动时间呢,案例中设置的0.01但是我改了一下没有变化
Kai Zhang
2024-05-24 COMSOL 员工在博客案例中如果是修改触发时间 tau, 可以看到不同的启动差异,建议适当增大该数值进行对比。
如泽 柳
2024-06-07你好最近在做电磁力计算相关的研究,在按照上述步骤添加条件后没有产生电磁力大概是什么原因造成的, 单独对用永磁铁或线圈进行仿真都可以仿真。方便给下邮件交流一下吗
没延 韩
2024-06-14 COMSOL 员工有可能是“连续性”里没把“一致边界对”加进来。所以装配体两侧磁场不连续没有电磁力。
Zexia He
2024-06-15您好,该案例现在有适用于6.0版本的 模型和文档教程可供下载学习吗?
hao huang
2024-06-17 COMSOL 员工您好
感谢您的评论
目前案例为最新版本,6.0版本暂时无法提供。
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
志伟 张
2024-07-03你好,我希望将案例中线圈的激励从方波电流源改为直流电压源,但是直接调整后仿真无法运行,请问我应该如何正确设置呢
Alex Zhang
2024-07-09 COMSOL 员工有可能是由于直流电压源电压过大,建议尝试“辅助扫描”的功能,由小到大逐步增大直流电压。
居敏 包
2024-07-24电磁阀回路是一个典型的电感电路,线圈激励采用电压,在考虑铁心引起的反电动势的情况下,可以求出线圈电流的变化波形吗?
Alex Zhang
2024-08-01 COMSOL 员工可以的。您可以尝试修改相关设置。