在使用旋转零件时,稳定性分析至关重要,因为不稳定性会导致灾难性故障。旋转系统会因为圆盘的不对称惯性、轴的不对称刚度或轴承引起的交叉耦合效应而导致不稳定的响应。从设计者的角度来看,重要的是要确保潜在的不稳定模式不在机器的工作范围内。本篇博文,让我们来探索如何使用 COMSOL Multiphysics® 软件预测转子系统的不稳定性。
什么是稳定性?
稳定性 可以定义为系统移回其初始平衡位置的趋势。稳定性可分为:
- 静态
- 动态的
下面,我们分别讨论这两种类型的稳定性。
静稳定性 是基于系统从平衡状态受到干扰时的初始响应,可进一步分为以下几种情况:
- 静态稳定:扰动后,物体趋向于回到平衡位置
- 静态不稳定:物体倾向于沿着扰动的方向继续运动,而不是回到平衡位置
- 中性稳定:受扰动后,物体在扰动方向保持平衡
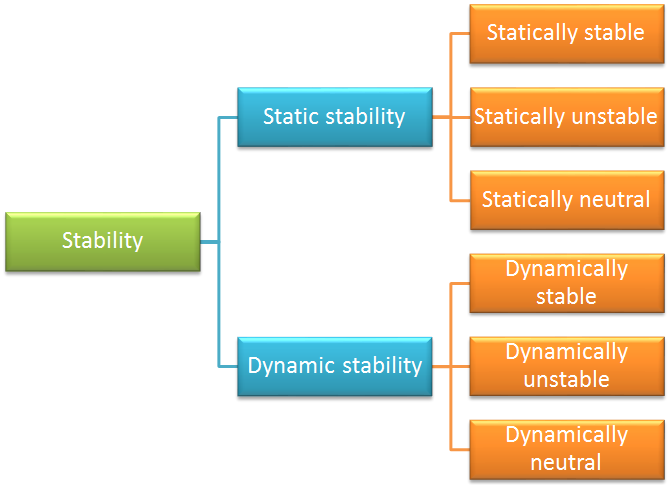
稳定性分类。
动态稳定性 是基于系统从其平衡位置受到干扰后的运动时间历程,可进一步分为以下几种情况:
- 动态稳定:系统的运动随时间而减少
- 动态不稳定:系统的运动随着时间而增加
- 动态中性:系统的运动随着时间保持不变
这些运动也大致分为两类:振荡和非振荡。
不同阻尼系数值的振荡运动(左)和非振荡运动(右)的响应。
现在我们已经熟悉了基本术语,接下来我们来了解稳定性的数学定义和系统变得不稳定的条件。
定义稳定性条件
惯性运动的一般动力学方程如下:
其中,[\textbf M],[\textbf C],[\textbf K] 分别表示质量、阻尼和刚度矩阵;\{\textbf u\},\{\textbf F\} 表示位移和力矢量。
动力学方程的解可以分为以下四类之一:
- 无阻尼
- 过阻尼
- 欠阻尼
- 临界阻尼
如果所有的系数都是正的,那么控制方程的解也是有界限的并且表现良好。然而,在某些情况下,系数变为负值,解变得无界限。为了理解这个问题,让我们来看看弹簧-质量-阻尼器系统在各种情况下的响应,如下图所示。
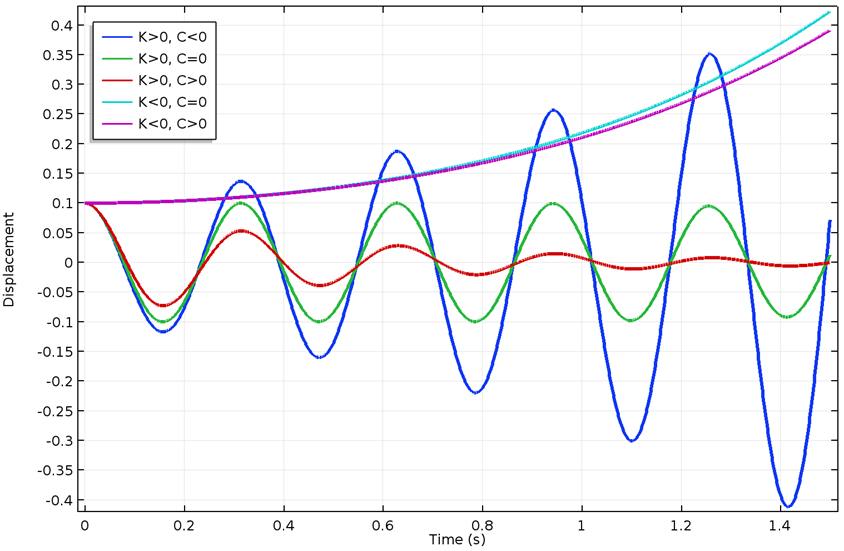
不同刚度和阻尼系数的响应。
从系统的预测响应中,我们可以说,当系统的刚度为负值时,系统是静态不稳定的;如果阻尼为负值,则系统是动态不稳定的。我们也可以从上图中发现,系统静态稳定才能实现动态稳定。然而,情况并非总是如此,尤其是当陀螺效应出现时。一个常见的例子是自行车,它是静态不稳定,但在一定速度范围内动态稳定。
线性稳定性分析可以用来预测系统的不稳定性。线性稳定性分析框架包括以下步骤:

典型线性稳定性分析的工作流程。
一旦特征值可用,稳定性可以根据特征值的系数值来决定。
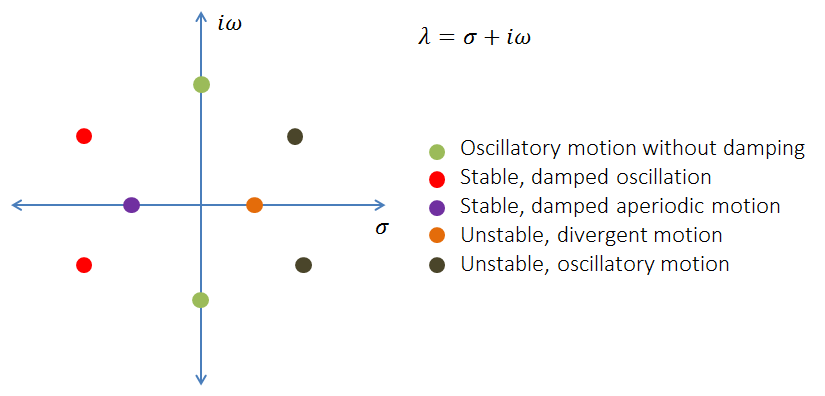
更好的方法不是比较系数,而是跟踪对数衰减,对数衰减被定义为 \delta= -2\cdot\pi\cdot\frac{\sigma}{\omega}。我们可以使用对数衰减量将系统的稳定性分类为:
| 值 | 行为类型 |
|---|---|
| \delta < 0 | 不稳定的 |
| \delta > 0 | 稳定的 |
不稳定的条件。
为了计算对数衰减量,我们可以将特征值写成 \delta= -2\cdot\pi\cdot\frac{\Re(\lambda)}{\Im(\lambda)},如果是本征频率,那么应该被写成 \delta= 2\cdot\pi\cdot\frac{\Im(\omega)}{\Re(\omega)}。
转子动力学问题的运动方程
转子动力学问题不同于传统的振动分析。附加项的出现是因为运动方程中存在附加的加速力项,这取决于所选的物理性质。
在转子动力学模块有两种方法可以解决这个问题。实心转子在旋转坐标系中形成,而梁转子在固定坐标系中形成。基于所选的物理场,运动方程中出现的附加项和效应如下所示:
| 固定坐标系(梁转子) | 旋转坐标系(实心转子) |
|---|---|
| 陀螺力矩 | 科里奥利力 |
| 无离心软化;用线表示的几何图形 | 离心软化 |
| 无离心硬化 | 离心硬化 |
| 内部阻尼贡献 | 外部阻尼贡献 |
现在,让我们看看这些项如何影响刚度和阻尼矩阵。
实心转子
实心转子在旋转坐标系中建模,因此在该坐标系中不会观察到转子的物理旋转。在动量平衡方程中,旋转的影响被解释为坐标系加速力。因为这个运动方程包含附加的项,所以旋转坐标系中的运动方程是:
其中,\textbf M 是质量矩阵;\textbf C_c 是科里奥利力效应的贡献(取决于转子的速度);\textbf C 是外部(固定)和内部(旋转)阻尼的贡献;\textbf K_c 是旋转坐标系中外部阻尼的贡献(取决于转子的速度);\textbf K是由内部刚度、外部刚度、离心软化和应力硬化引起的刚度矩阵;\textbf F 是旋转坐标系中的力。
对于实心转子,没有陀螺项;相反,会得到离心力(与刚度矩阵的对称部分结合在一起)、科里奥利力(作为阻尼矩阵的反对称部分出现)、欧拉力(作为反对称刚度矩阵出现),以及作为刚度矩阵反对称项中的外部阻尼的贡献。
梁转子
梁转子在固定坐标系中建模。旋转坐标系的运动方程为:
其中,\textbf M 是质量矩阵;\textbf C_g 是陀螺效应的贡献(取决于转子的速度);\textbf C 是外部(静止)和内部(旋转)阻尼的贡献;\textbf K_c 是固定坐标系中内部阻尼的贡献(取决于转子的速度);\textbf K 是刚度矩阵;\textbf F 是力矢量,包含力和力矩(梁上的弯矩和扭矩)。
在梁转子中,陀螺项构成了阻尼矩阵的反对称部分,内部阻尼在刚度矩阵中表现为反对称项。
刚度和阻尼系数如何影响转子系统
考虑一个与全局x-轴对齐的轴。转子上的局部y和z方向与全局y和z方向相同方向。
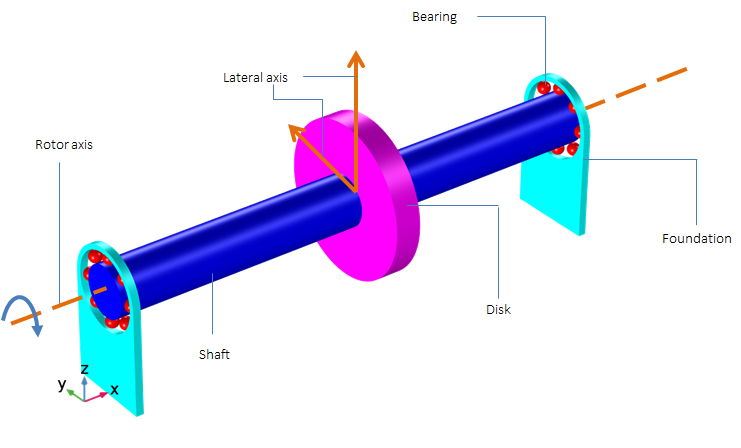
显示转子系统组件的示意图。
对于转子动力学问题,横向运动方程是耦合的;因此,它们比轴向和扭转振动的方程更复杂。在本节中,我们将讨论直接刚度和交叉耦合刚度对转子横向运动的影响。考虑一个对称的转子,两边都有对称的轴承。轴承包含直接和交叉耦合项。
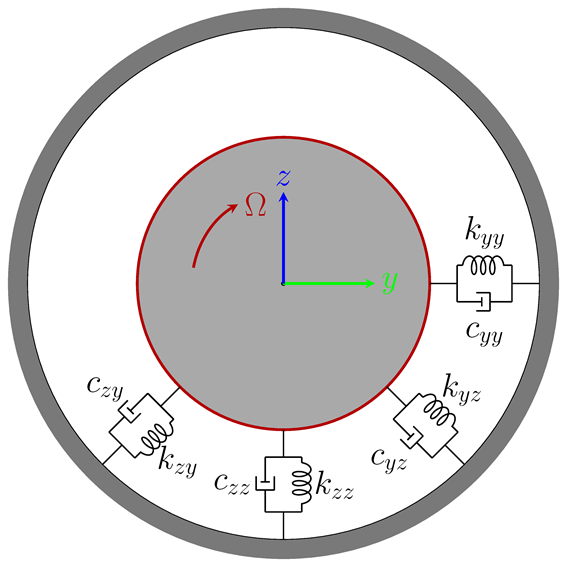
带有直接和交叉耦合项的轴承示意图。
如果我们把各个方向的力写成矩阵形式,可以写成:
\textbf F_y \\
\textbf F_z
\end{Bmatrix}=-
\begin{bmatrix}
\textbf K_{yy} & \textbf K_{yz}\\
\textbf K_{zy} & \textbf K_{zz}
\end{bmatrix}
\begin{Bmatrix}
\textbf y \\
\textbf z
\end{Bmatrix}-
\begin{bmatrix}
\textbf C_{yy} & \textbf C_{yz}\\
\textbf C_{zy} & \textbf C_{zz}
\end{bmatrix}
\begin{Bmatrix}
\mathbf{\dot{y}} \\
\mathbf{\dot{z}}
\end{Bmatrix}
所以,y 和 z 方向的力可以写成:
\textbf F_y = -K_{yy}\cdot\textbf y -K_{yz}\cdot\textbf z -C_{yy}\cdot \dot{\textbf y}- C_{yz}\cdot \dot{\textbf z}\\
\textbf F_z = -K_{zy}\cdot\textbf y -K_{zz}\cdot\textbf z -C_{zy}\cdot \dot{\textbf y}- C_{zz}\cdot \dot{\textbf z}
\end{matrix}
让我们讨论每个项对转子系统横向运动的单独影响。根据输入,有两种类型的旋转模式:向前和向后。在向前旋转的情况下,转子的轨道运动和旋转方向是相同的,而向后旋转则相反。
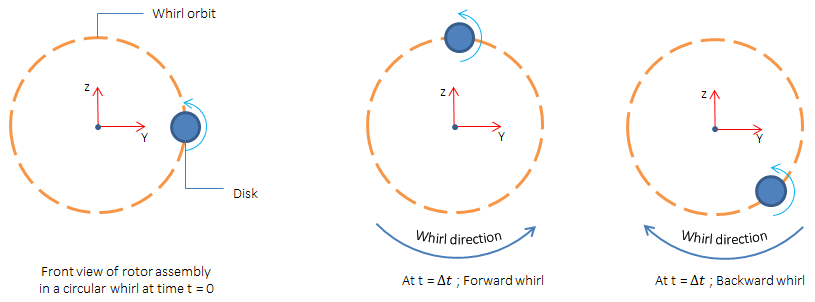
显示前后旋转的示意图。
直接系数
直接刚度项(\textbf K_{yy}, \textbf K_{zz})影响偏转矢量方向的力。如果系数为正,那么力的方向与偏转方向相反。如果系数值为负,则力与挠度方向相同。
正直接阻尼项(\textbf C_{yy}, \textbf C_{zz})产生一个垂直于偏转矢量的力,方向与涡旋速度方向相反。如果数值为负,力的方向是旋转速度方向。
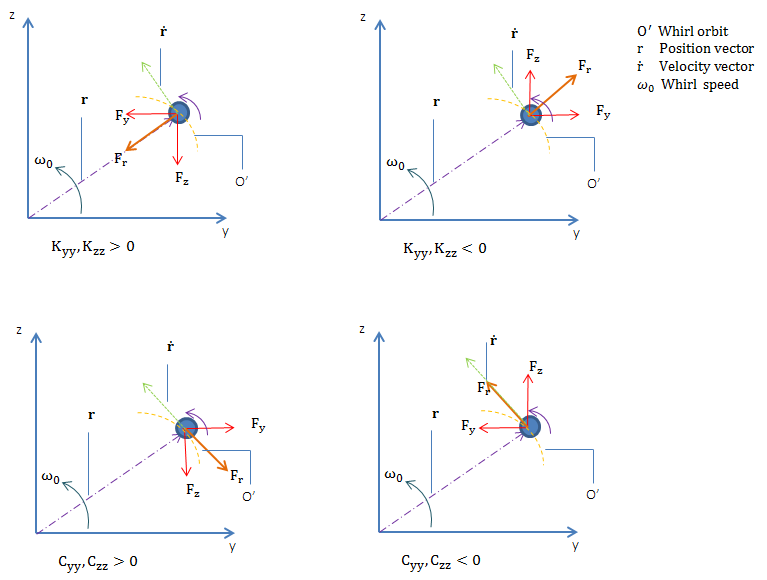
直接刚度和阻尼系数的力图(前旋)。
交叉耦合系数
如果 \textbf K_{yz}, \textbf K_{zy} 同号,根据系数的符号,它们会产生一个与偏转向量方向相同或相反的力。如果 \textbf K_{yz}, \textbf K_{zy} 的值不一样,就会使旋转变成椭圆形。
如果 \textbf K_{yz}, \textbf K_{zy} 有相反的符号,则它们会产生一个垂直于偏转向量的力。方向取决于系数的符号。
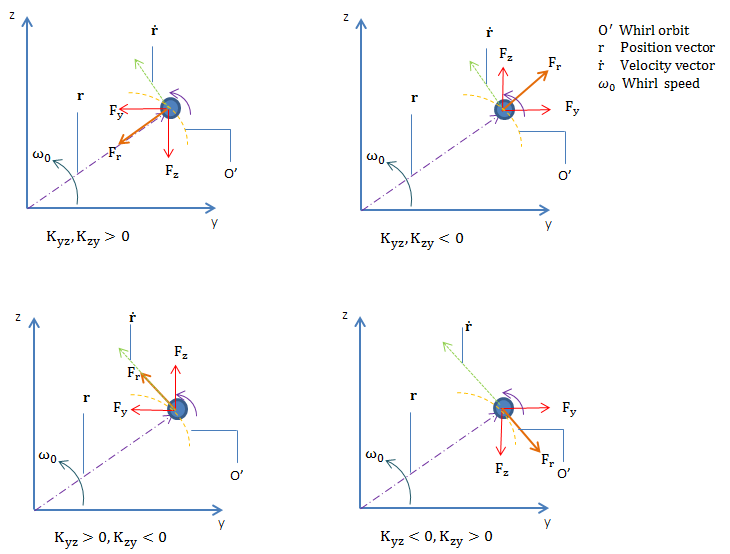
交叉耦合刚度系数的力图(正向涡动)。
如果 \textbf C_{yz}, \textbf C_{zy} 同号,它们产生一个垂直于偏转向量的力。方向取决于系数的符号。如果 \textbf C_{yz}, \textbf C_{zy} 不同号,它产生一个与偏转向量共线的力,符号取决于系数。这会产生硬化或去硬化效应。例如,如果 \textbf C_{yz}>0, \textbf C_{zy}<0,力的方向与偏转矢量相反,会产生硬化效应。
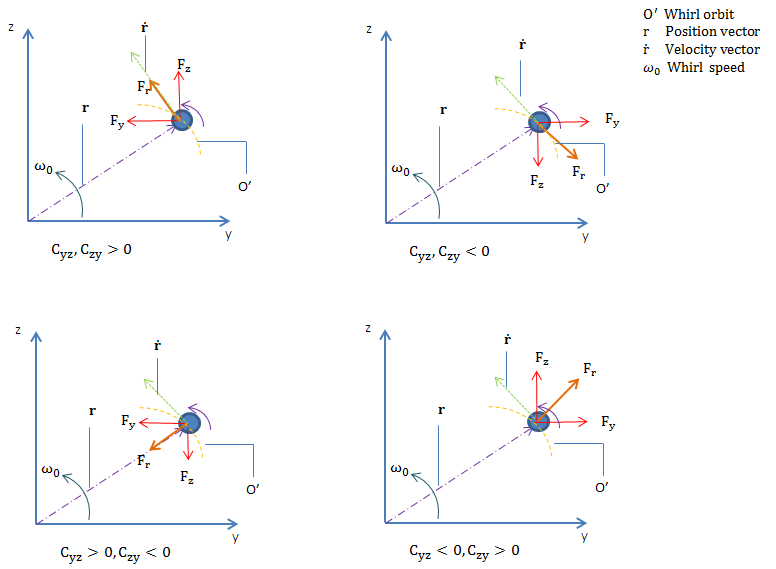
交叉耦合阻尼系数的力图(正向涡动)。
简而言之,产生径向力的项(直接刚度和交叉耦合阻尼)不会导致系统不稳定,而产生与涡旋轨道相切的力的项会导致系统不稳定。该系数的影响也根据涡动模式而变化。例如,如果 \textbf K_{yz}(+ve), \textbf K_{zy}(-ve),它会产生一个与涡动轨道相切的力,这个力会使前向涡动不稳定,使后向涡动稳定。基于旋转模式的效果总结如下:
| 系数 | 向前旋转 | 反向旋转 | 力的方向 |
|---|---|---|---|
| \textbf K_{yy}, \textbf K_{zz} >0 | 稳定性处理 | 稳定性处理 | 径向 |
| \textbf K_{yy}, \textbf K_{zz} <0 | 使不稳定 | 使不稳定 | 径向 |
| \textbf K_{yz}, \textbf K_{zy} >0 | 稳定性处理 | 稳定性处理 | 径向 |
| \textbf K_{yz}, \textbf K_{zy} <0 | 稳定性处理 | 稳定性处理 | 径向 |
| \textbf K_{yz}>0, \textbf K_{zy}<0 | 使不稳定 | 稳定性处理 | 与旋转轨道相切 |
| \textbf K_{yz}0 | 稳定性处理 | 使不稳定 | 与旋转轨道相切 |
| \textbf C_{yz}, \textbf C_{zy} >0 | 使不稳定 | 使不稳定 | 与旋转轨道相切 |
| \textbf C_{yz}, \textbf C_{zy} <0 | 稳定性处理 | 稳定化处理 | 与旋转轨道相切 |
| \textbf C_{yy}, \textbf C_{zz} >0 | 稳定性处理 | 稳定性处理 | 与旋转轨道相切 |
| \textbf C_{yy}, \textbf C_{zz} <0 | 使不稳定 | 使不稳定 | 与旋转轨道相切 |
| \textbf C_{yz}>0, \textbf C_{zy}<0 | 稳定性处理 | 稳定性处理 | 径向 |
| \textbf C_{yz}0 | 稳定性处理 | 稳定性处理 | 径向 |
转子系统稳定性分析
作为一名设计师,几乎不可能创造出完美的转子,因为模型中总是存在一些不对称。不对称可能是由于质量分布,也可能是由于形状造成的刚度。此外,转子可能会受到交叉耦合力、内部摩擦、转子摩擦和汽流涡旋的影响。这些条件的存在会影响转子系统的稳定性。我们来看几个这样的案例…
轴承引起的不稳定性分析
在轴承中,交叉耦合力是不稳定的关键原因。交叉耦合力导致系统阻尼的快速损失,并导致转子次同步振动。在某些情况下,这可能导致零阻尼或负阻尼,从而使系统不稳定。
如果轴沿着 x-轴,然后按照惯例,交叉耦合力以矩阵形式书写,如下所示:
\textbf F_y\\
\textbf F_z
\end{Bmatrix}=-
\begin{bmatrix}
0 &\textbf K_{yz}) \\
-\textbf K_{yz}& 0
\end{bmatrix}
\begin{Bmatrix}
\textbf y\\
\textbf z
\end{Bmatrix}
通常,在液体动压轴承中,交叉耦合力在转子中起到负阻尼的作用。当接近临界速度时,这些力会导致不受控制的振动,甚至导致轴承故障。
COMSOL案例库中的模型讨论了交叉耦合力引起的稳定性。该模型包括一个涡轮增压器转子,由两个轴承支撑:一个靠近压缩机,另一个靠近涡轮机,使压缩机和涡轮机都悬挂在轴上。
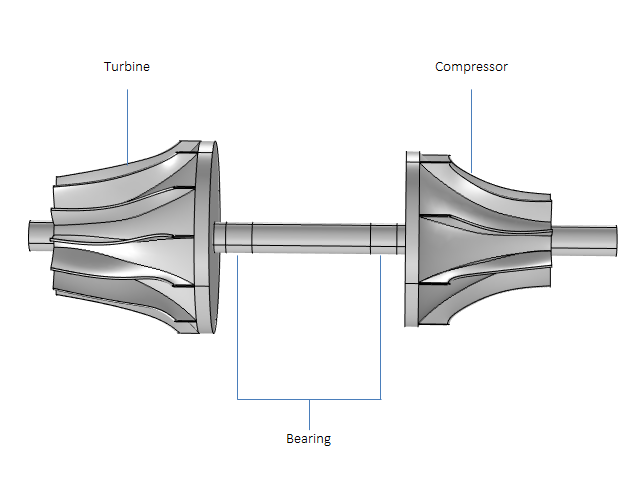
带轴承的涡轮增压器。
针对两种情况进行分析,一种是没有交叉耦合力,另一种是有交叉耦合力。在 COMSOL Multiphysics 中,有三种不同的方式来包含轴承的交叉耦合效应:
- 如果交叉耦合刚度已知,它可以直接被指定为 轴承节点下的非对角项
- 如果力是已知的,可以在轴承 节点 使用 力和力矩 选项
- 为了捕捉轴承的完全非线性效应,可以直接将转子模拟与流体动力轴承模拟耦合起来
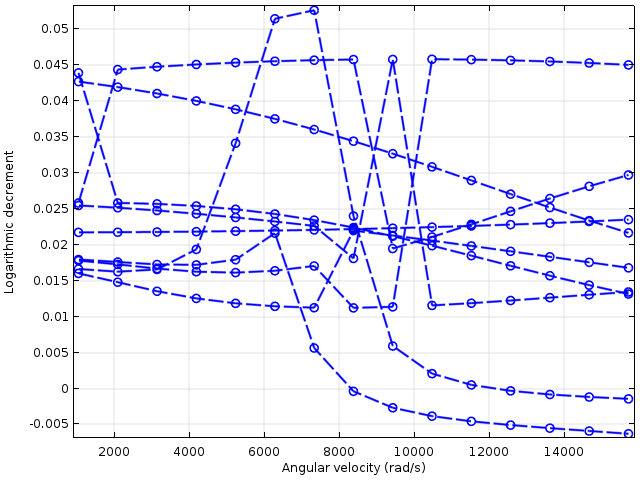
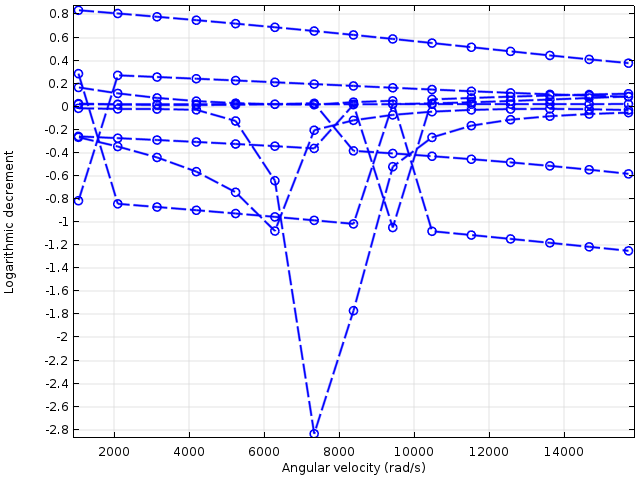
不带(左)和带(右)交叉耦合项的对数衰减量。
在上面的图中,在没有交叉耦合刚度的情况下,对数衰减大部分是正的,表明固有模式是稳定的。只有在高转速下,才会有一些模式变得不稳定。在存在交叉耦合刚度的情况下,许多模态具有负对数衰减,即使在低转子速度下也是如此。
结果表明,交叉耦合刚度的存在使振动模式不稳定,因此在这些速度下运行涡轮增压器转子是危险的。
旋转阻尼引起的不稳定性
机械耗散的元素会导致不稳定,这听起来很奇怪,但在旋转组件的情况下,这是真的。由于旋转阻尼附着在物体上,所以它位于旋转坐标系中。在静止坐标系中进行坐标变换后,它不再仅仅依赖于速度。这种转变导致耗散项和循环项,它们取决于转子速度和位移。循环项是一个不稳定的原因。
\mathbf{F_y}\\
\mathbf{F_z}
\end{Bmatrix}=
\begin{bmatrix}
\mathbf{C_i}&\mathbf{0} \\
\mathbf{0}& \mathbf{C_i}
\end{bmatrix}
\begin{Bmatrix}
\mathbf{\dot{y}}\\
\mathbf{\dot{z}}
\end{Bmatrix}
+
\begin{bmatrix}
\mathbf{0}&\mathbf{(C_i\cdot\omega)} \\
\mathbf{-(C_i\cdot\omega)}& 0
\end{bmatrix}
\begin{Bmatrix}
\mathbf{y}\\
\mathbf{z}
\end{Bmatrix}
其中,\omega 是转子旋转速度。
考虑一个 Laval-Jeffcott 转子,它由一个无质量的轴和一个由两端具有对称阻尼和刚度的两个相同轴承支撑的圆盘组成。现在,如果旋转阻尼效应也包含在系统中,循环项出现在控制方程中会导致不稳定。
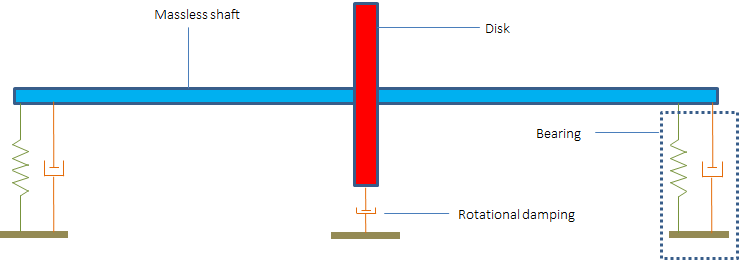
有内部阻尼的 Laval-Jeffcott 转子示意图。
为了进一步研究这种影响,我们来画一个系统的力图。从力图中可以清楚地看出,循环项在向前旋转的运动方向上产生力。这意味着循环项是在给系统增加能量,由于外部阻尼而产生的耗散项是在不断地从系统中移除能量。
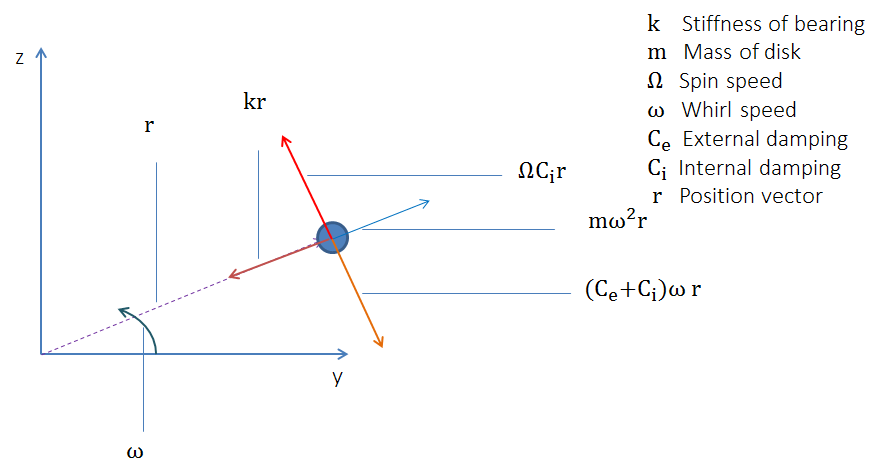
有内部阻尼的 Laval-Jeffcott 旋子的力图。
从力图中,我们可以说条件 \Omega = \omega \frac{C_e+C_i}{C_i} 在异步涡动条件下触发不稳定性。当旋转速度和旋转频率不同时,就会发生异步旋转。转子的内部阻尼是由材料的滞后阻尼或冷缩配合零件界面摩擦产生的库仑阻尼产生的。
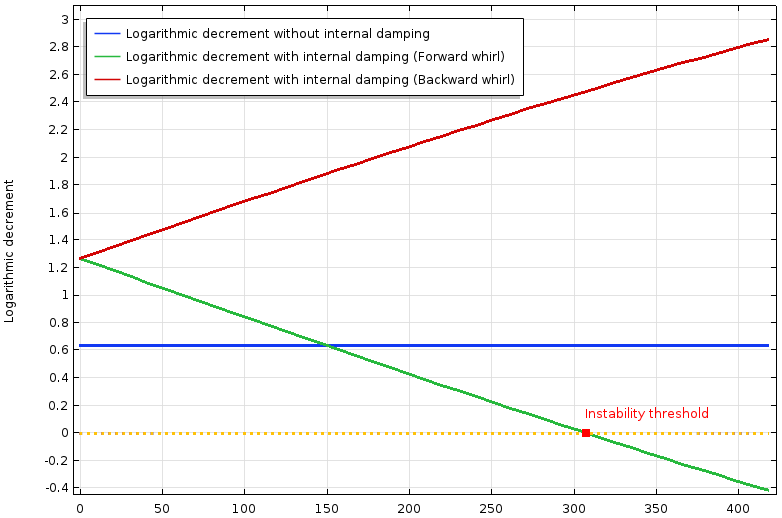
无内部阻尼(蓝色)和有内部阻尼(红色和绿色)的 Laval-Jeffcott 转子的对数衰减。
上图比较了有内部阻尼和没有内部阻尼的转子模型。交叉耦合项产生的力本质上是非保守的。内部阻尼作为交叉耦合项对刚度矩阵有贡献,它取决于速度,所以对数衰减不是常数,随速度而变化。对数衰减是针对两种初始模式(向前和向后模式)绘制的。在零自旋时,两种模式具有相同的对数衰减。随着速度的增加,后向涡动的对数衰减增加,前向涡动的对数衰减减小,最终变为负值。这证实了交叉耦合项使后向涡动稳定,并使前向涡动不稳定。
如果我们进行频域分析,结果与没有阻尼的情况相同,并且涡动是圆形的。这意味着模型中只有向前的涡动。
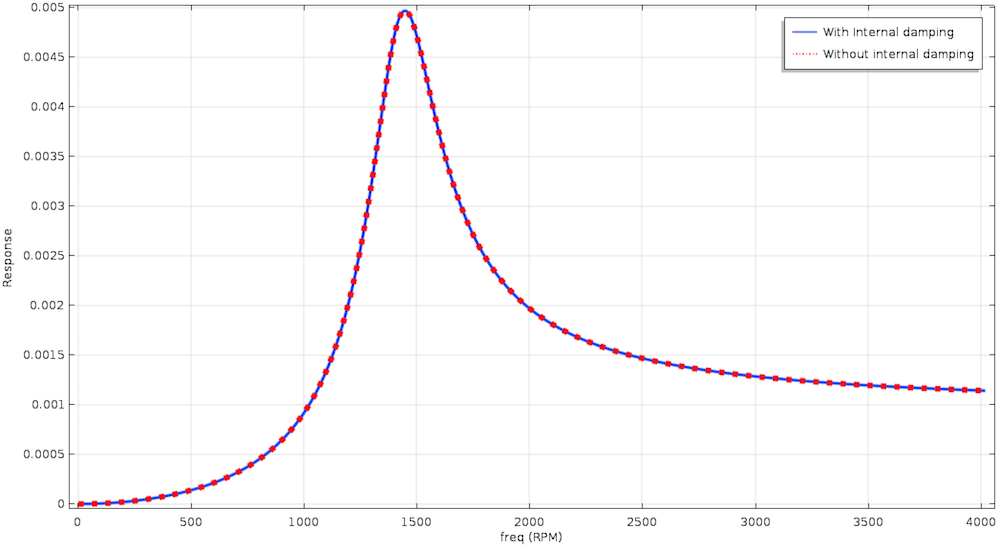
有和没有内部阻尼的 Laval-Jeffcott 转子的频率响应。
由于旋转阻尼引起的交叉耦合项仅影响阻尼特性,而不改变系统的响应。现在,如果我们看坎贝尔(Campbell)图,自然频率不再是一个恒定值,或者如果有内部阻尼,它会随着速度而增加。在内部阻尼的情况下,或者如果我们想用坎贝尔图找到不稳定性阈值,这种效应会增加阻尼临界速度。然后,我们可以画一条线 \omega=\Omega(\frac{C_i}{C_i+C_e})\,线与自然频率的交点给出了阈值。
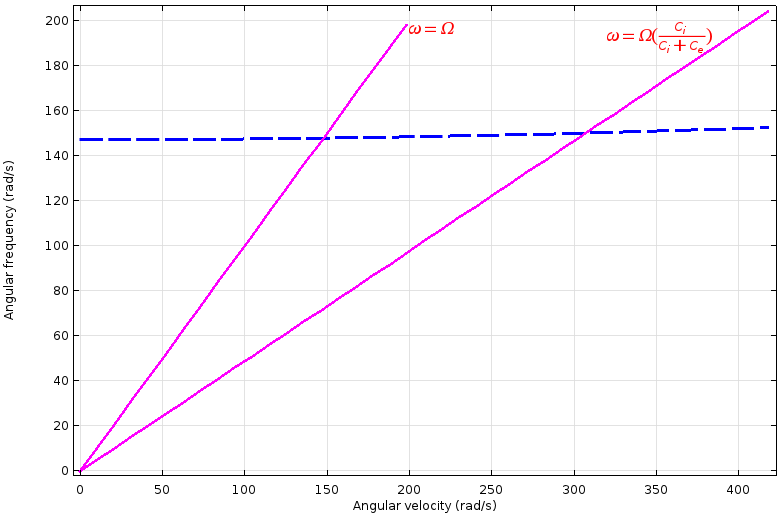
初始模式下有内部阻尼的 Laval-Jeffcott转子的坎贝尔图。
蒸汽涡动引起的不稳定性
当沿圆周发生渗漏导致径向位移时,在轴流式机器(如燃气轮机)中会产生蒸汽涡动。这会产生一个垂直于位移的合力。激发出来的力在某些工况下产生不稳定性,在另一些工况下产生稳定性。蒸汽旋转力以反对称的方式增加了刚度项,就像内部阻尼一样,但不依赖于旋转速度。
\mathbf{F_y}\\
\mathbf{F_z}
\end{Bmatrix}=
\begin{bmatrix}
\mathbf{0}&\mathbf{(K_{sw})} \\
-\mathbf{(K_{sw})}& 0
\end{bmatrix}
\begin{Bmatrix}
\mathbf{y}\\
\mathbf{z}
\end{Bmatrix}
为了更容易理解这种影响,我们来讨论在蒸汽涡动作用下,具有外部阻尼和刚度的Laval-Jeffcott转子的力图。
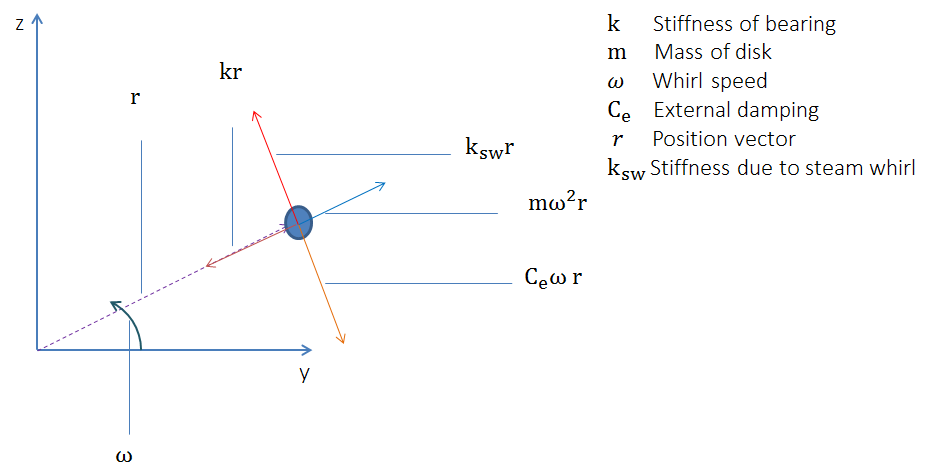
有蒸汽涡动的 Laval-Jeffcott 转子的力图。
从力图中,我们可以看到什么时候达到稳定阈值 K_{sw}=C_e\cdot\omega_n,其中 \text{\math{\omega_n}$} 是自然频率。这意味着可以通过增加外部阻尼或固有频率来提高稳定性阈值。
让考虑拉 Laval-Jeffcott 转子,由于反对称项,系统最初是不稳定的。如果我们在系统中引入外部阻尼,对数衰减将趋近于零,最终变为正值。通过增加外部阻尼的值,可以增加系统不稳定阈值的频率值。
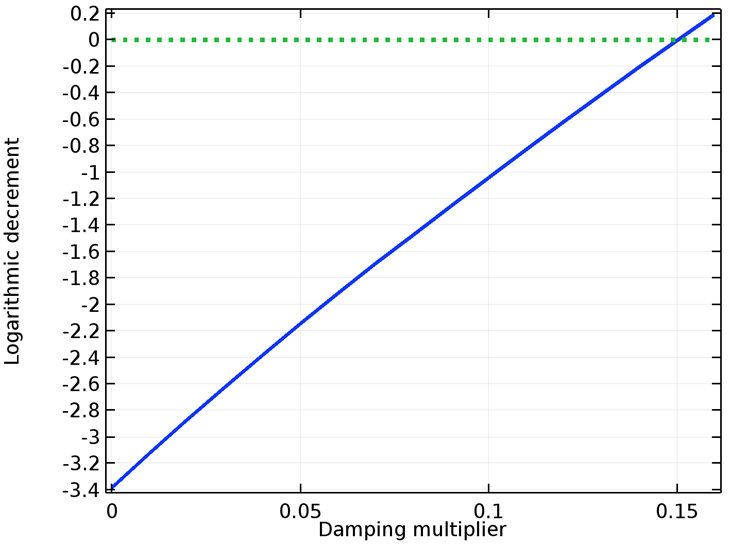
具有固定端和蒸汽涡动的Laval-Jeffcott转子的对数衰减。
结束语
在这篇博客文章中,我们讨论了稳定性的类型、阻尼和刚度矩阵系数对系统响应的影响、实心转子和梁转子物理场的控制方程、使用特征频率分析预测系统不稳定性的方法以及导致转子系统不稳定性的一些应用。
后续步骤
单击下面的按钮,了解更多关于旋转动力学模块(COMSOL Multiphysics 和结构力学模块的附加模块)中旋转系统建模的专门功能。



评论 (0)