
压电现象被广泛应用在各种工程应用上,包括传感器、喷墨打印头、自适应光学器件、开关设备、手机组件和吉他拾音器,等等。今天我们将为您介绍压电理论和基本模拟的一些基础要素,以及改善压电驱动器运动范围的新颍设计,提供一些模拟“技巧”,为压电学的初学者和专家提供一些参考。
压电理论的数学惯例
在开始讨论压电物理之前,让我们先来复习几个数学惯例。压电材料具有应变极化的特性,反之亦然。前者被称为正压电效应,后者被称为逆压电效应。在数学中,通常用一组矩阵方程的两种形式来描述这些效应:应变–电荷型 (也称为 d 形)和应力-电荷型 (或 e 形)。这两种形式可以相互导出。
注:这两种形式是可以相互转换的,因此你可以选择你喜欢的形式。在 COMSOL Multiphysics 中,将应变-电荷型转换为应力-电荷型。
在这里,我们将选择d形,其中的关系可以表示为
\varepsilon & = s_E S + d^T \bf{E}\\
\bf{D} & = d\,S+\varepsilon_0 \varepsilon_{r} \bf{E}
其中,场量 \varepsilon,D,S 和 \bf{E} 分别是应变、电位移、应力和电场。
材料参数 s_E,d 和 \varepsilon_{r} 分别是柔度、耦合矩阵和相对介电常数。上标 T 代表转置。第一个方程表示应力场和电场产生应变的关系。同时,第二个方程显示了应力场和电场产生的极化。第一个方程的第二项说明了电场对应变的贡献。
在固体力学中,我们通常考虑一个虚构的小微分体积来理解施加在体积上的力。考虑这样一个小六面体,其表面与全局笛卡尔坐标系的每个轴对齐(xyz-轴)。
用6个不同的量描述虚构体积表面上单位面积上的力。其中3个垂直于每个表面,通常用\sigma_{xx},\sigma_{yy}和\sigma_{yy} 表示。另外 3 个平行于每个表面\tau_{yz}, 用\tau_{xz}和 \tau_{xy}表示(\tau_{zy}, \tau_{zx} 和 \tau_{yx} 因为对称而被省略。)
下角标第一个字母表示所在表面的法向。第二个字母表示力的方向。比如,\sigma_{xx} 是施加在 yz 平面(垂直于 x 轴)上沿着 x 轴方向的力;\tau_{yz} 是在 xz 平面上沿着 z 轴的力;诸如此类。
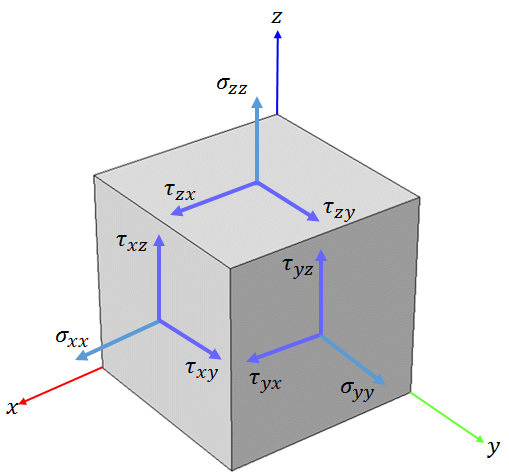
小微分立方体积中的力分量。
这 6 个量通常用一个列向量表示。在 COMSOL Multiphysics 中,量的顺序有两种约定: 一种是标准符号,另一种是 Voigt 符号。在 COMSOL Multiphysics 中的压电器件 接口中一定要使用 Voigt 符号,这非常重要。(在固体力学 接口默认使用标准符号。)
在 Voigt 符号中,应力被写成 6×1 列向量(应特别注意 yz-,xz- 和 xy- 分量的顺序):
\begin{array}{c}
\sigma_{xx} \\
\sigma_{yy} \\
\sigma_{zz} \\
\tau_{yz} \\
\tau_{xz} \\
\tau_{xy}
\end{array}
\right )
同样,应变可以写成
\begin{array}{c}
\varepsilon_{xx} \\
\varepsilon_{yy} \\
\varepsilon_{zz} \\
2 \varepsilon_{yz} \\
2 \varepsilon_{xz} \\
2 \varepsilon_{xy}
\end{array}
\right )
在 COMSOL Multiphysics 中,耦合矩阵 d 由下式定义
=
\left (
\begin{array}{cccccc}
d_{xxx} & d_{xyy} & d_{xzz} & d_{xyz} & d_{xxz} & d_{xxy} \\
d_{yxx} & d_{yyy} & d_{yzz} & d_{yyz} & d_{yxz} & d_{yxy} \\
d_{zxx} & d_{zyy} & d_{zzz} & d_{zyz} & d_{zxz} & d_{zxy}
\end{array}
\right )
这里,符号 d_{xyz} 为由电场分量 E_x 引起的应变分量的耦合系数 \varepsilon_{yz} 。现在,在 Voigt 符号中,所有下标都是数字,规则是:
因此,耦合系数矩阵可以表示为
=
\left (
\begin{array}{cccccc}
d_{11} & d_{12} & d_{13} & d_{14} & d_{15} & d_{16} \\
d_{21} & d_{22} & d_{23} & d_{24} & d_{25} & d_{26} \\
d_{31} & d_{32} & d_{33} & d_{34} & d_{35} & d_{36}
\end{array}
\right )
同样,电贡献可以改写为
\begin{array}{c}
\varepsilon_1 \\
\varepsilon_2 \\
\varepsilon_3 \\
\varepsilon_4 \\
\varepsilon_5 \\
\varepsilon_6
\end{array}
\right )
=
\left (
\begin{array}{ccc}
d_{11} & d_{21} & d_{31} \\
d_{12} & d_{22} & d_{32} \\
d_{13} & d_{23} & d_{33} \\
d_{14} & d_{24} & d_{34} \\
d_{15} & d_{25} & d_{35} \\
d_{16} & d_{26} & d_{36}
\end{array}
\right )
\left (
\begin{array}{c}
E_1 \\
E_2 \\
E_3
\end{array}
\right ).
在 COMSOL Multiphysics 中的材料属性设置中,为了简洁起见,矩阵 d 被展平成一个1×18的行向量,如下所示:
,d_{22},d_{23},d_{24},d_{25},d_{26},d_{31},d_{32},d_{33},d_{34},d_{35},d_{36})
我们始终可以选择以矩阵形式查看表达式,可以通过点击“输出属性”中的 编辑 按钮实现,如下所示:
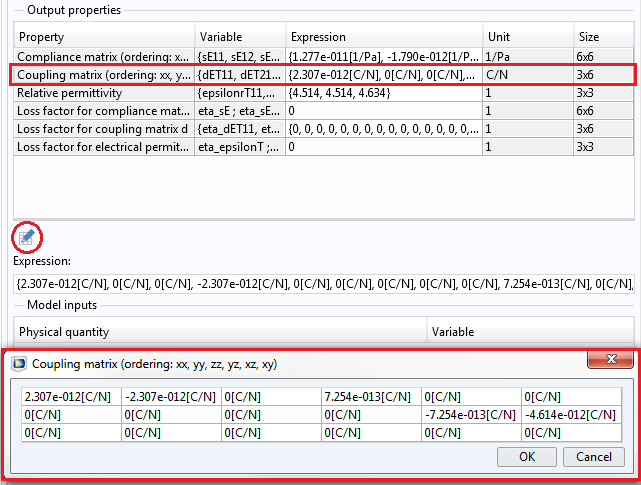
COMSOL 桌面截图,以矩阵形式显示的 d 系数。
基本压电模拟
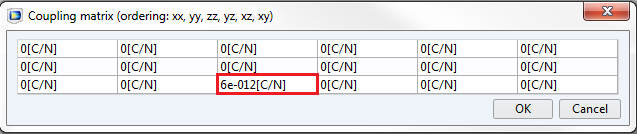
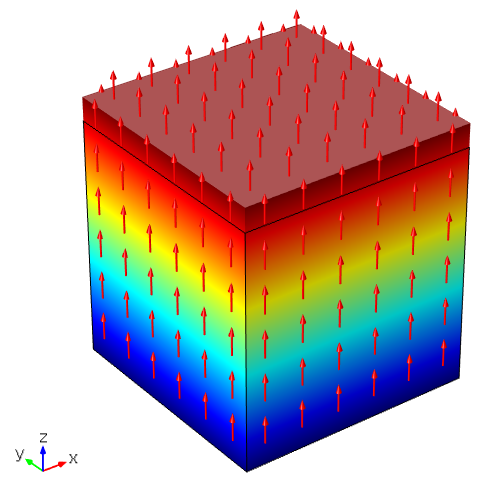
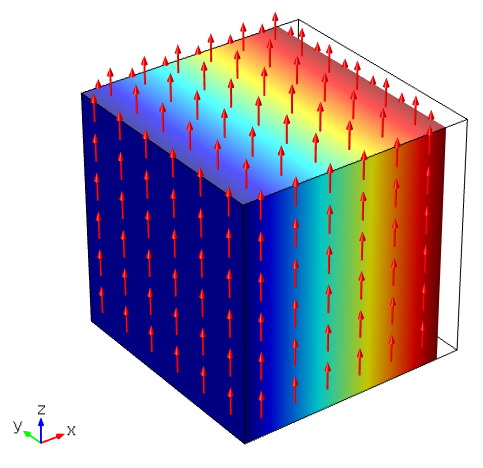
现在,我们已经复习了压电理论的一些基础知识。接下来,我们进行模拟。在这里,我们仅在以下位置输入一个非零数字 d_{33}。这意味着压电材料通过电场的 z-分量 E_{z} 产生一个沿 z 轴的力。同时,假设底面是机械固定的。
我们可以得到如下所示的结果,表面颜色表示总位移,箭头表示电场。电场对应变的贡献由 E_3d_{33} 给出。黑色轮廓表示最初未变形的形状。如图所示,体积在z-轴方向上拉伸。
d 系数只包含 d_{33}。在沿 z 轴的电场作用下,体积沿 z 轴拉伸。
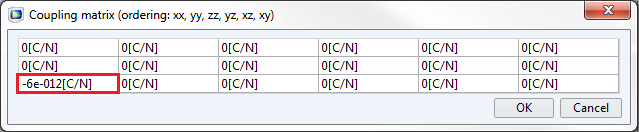
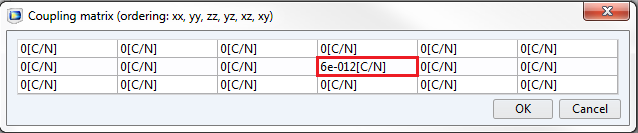
保持相同的电场,我们现在只输入一个负数 d_{31}。在 yz-平面机械固定的情况下,体积沿 x-轴方向缩小。
d 系数唯一非零负值 d_{23} 的示例,在沿 z 轴的电场作用下,体积在 x 轴缩小。
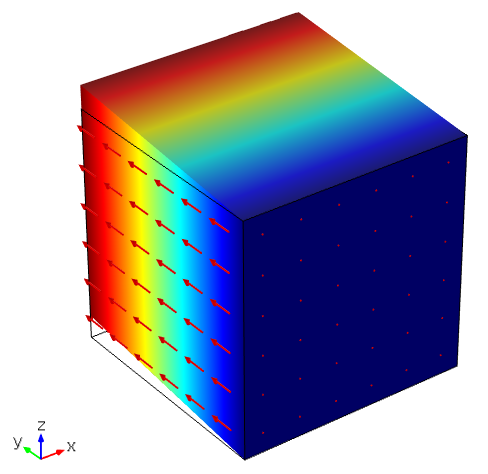
最后一个初步示例显示了一个剪切力,其中仅输入了一个非零数字 d_{24}
。XZ-平面是机械固定的,沿着 y-轴施加了一个电场。
d 系数中的唯一非零值的示例,。在沿 y 轴的电场作用下,体积沿 yz 平面有一个剪切力。
基于上述的基本要素介绍,我们将向您介绍一个设计压电执行器的有用技巧——压电“技巧”。
提高压电驱动器运动范围:一种新颍的设计
模拟压电悬臂梁,一种简单的MEMS器件
压电材料本身并不是 MEMS 器件。要成为这样的设备,必须将其连接到其他弹性材料上。悬臂是最简单的 MEMS 示例之一,并且有两种不同的压电类型。第一种是单晶 类型,它通常是通过将单层压电材料连接到弹性材料上而制成的薄片。另一个是双压电晶片 类型,它由两个压电层和其他弹性材料组成。用于连接的材料几乎可以是任何东西,只要能够在它们的表面上放置电极层。在这里,为了简单起见,我们将考虑单晶类型的 MEMS 器件。
值得一提的是,COMSOL Multiphysics 提供的所有压电材料特性都假定在局部坐标系的 z-轴上极化。如果材料沿另一个方向极化,您需要定义一个坐标系,使其第三个方向与极化方向对齐。
COMSOL Multiphysics 有设置局部坐标系的便捷功能。要了解更多信息,您可以参考《结构力学模块用户指南》第 106 页。您也可以在 MEMS 模块的压电器件 案例库以及我们的网站上的案例库中查看压电剪切驱动梁和厚度剪切模式石英振荡器模型。
在上面提到的假设下,我们模拟了一端固定的单压电晶片悬臂。在材料库中选择钛酸钡(BaTiO3)作为压电材料,二氧化硅(SiO2)作为基底。
MEMS 器件的原理很简单。在 z 方向上施加一个电场,由于d_{31} (=-7.8e-11 [C/N]),导致在 x 方向收缩。请注意,电极的弹性特性在这里没有模拟。为了获得 z-向电场,在钛酸钡的一侧施加电势,而另一侧接地。在左端固定的情况下,MEMS 悬臂的自由端移动约 9um。顶部材料(钛酸钡)收缩的同时会拉动底部材料(二氧化硅),导致整个器件向上弯曲。
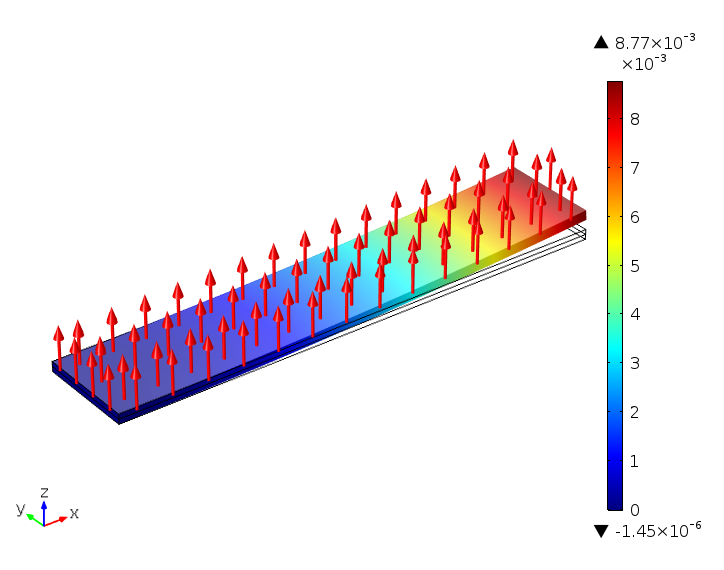
一端固定的单晶形态悬臂显示了总位移。
但是,如果出于某种原因——也许是机械强度——我们不得不固定设备的两端呢?结果是显而易见的:几乎没有位移,因为顶部材料无法沿着 x-轴收缩。更准确地说,唯一的位移 d_{32} 是由于产生的效果,这不是有意的。
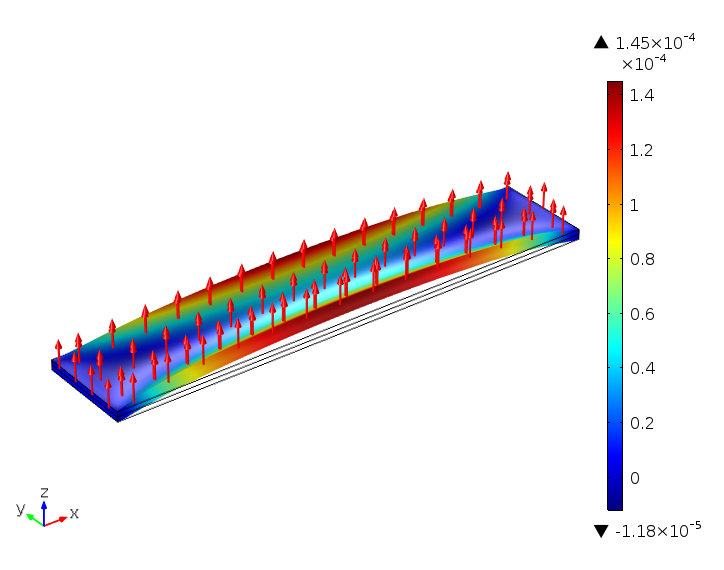
两端固定的单晶悬臂几乎没有位移。
然而,扭转这种情况是可能的。我们可以通过一个小小的“技巧”来修改压电器件。如下图所示,位移现在回到相同的数量级。如果你查看电场方向,可以发现我们为得到这个结果所做的工作是显而易见的。电场在梁的中心部分是反向的。你可以通过将电极分成三个部分来实现这个技巧:一个中心和两个边部,交替地将它们接地,并以相反的顺序交替地施加电压,如下面两个图形中的第一幅图所示。
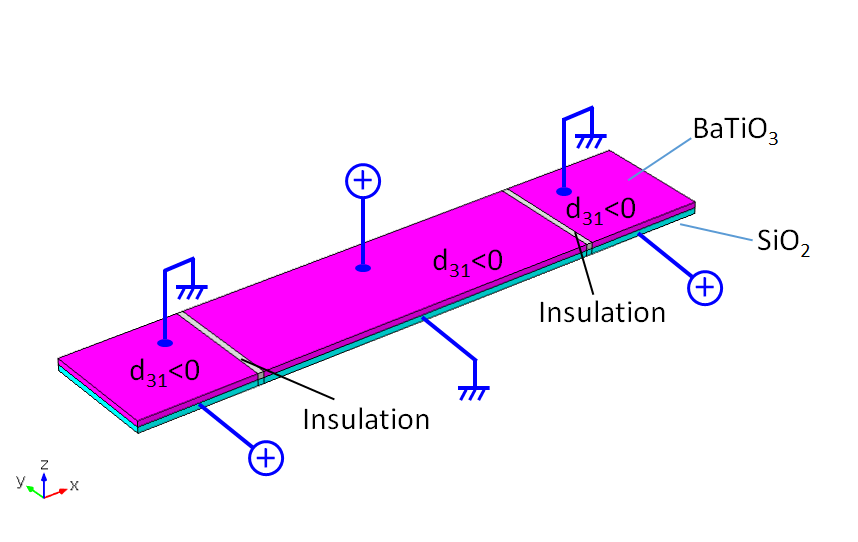
在交变电场下,两端固定的单晶悬臂的材料和电压配置。
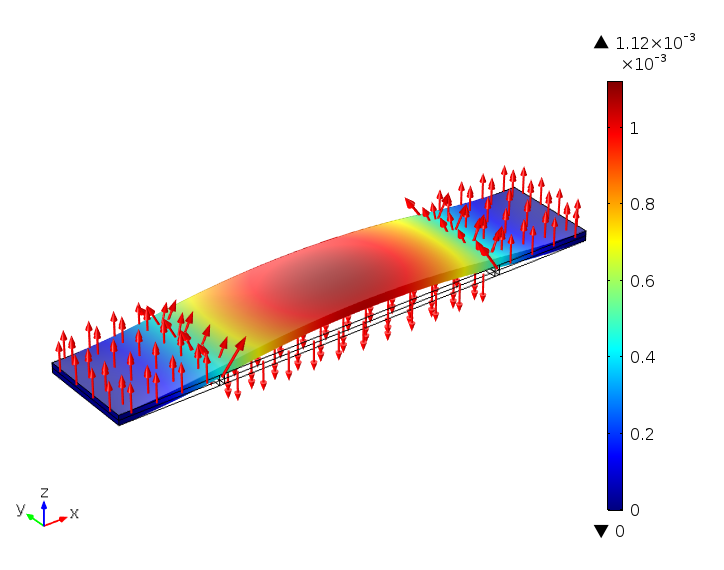
两端固定的单晶悬臂。施加交变电场可以提高总位移。
我们再来看一个例子。乍一看,这似乎有点神秘,因为整个电场都在同一个方向上。尽管如此,在不改变电场的情况下,我们仍能得到与前面结果相同的性能。相反,我们交替使用压电材料,将它分成三个部分(同样,一个中心和两个边部),并翻转中心部分。
我们可以通过使用不同的局部坐标系来完成模拟,或者在类似的简单情况下,可以通过改变耦合系数的符号d_{31}来完成。实际上,我们真的可以把压电材料分开,把翻转的部分放在中间。一种更简单、更实用的方法是以与前面示例相同的方式对电极进行构图,但在相反的方向上对中心部分进行极化。在这种情况下,无需拆分材料。
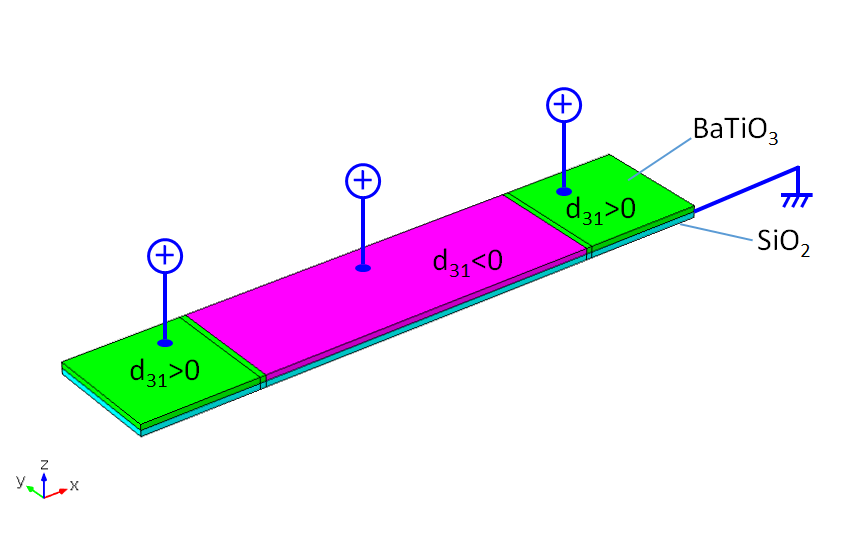
对于两端固定的单晶悬臂,材料和电压交替配置。
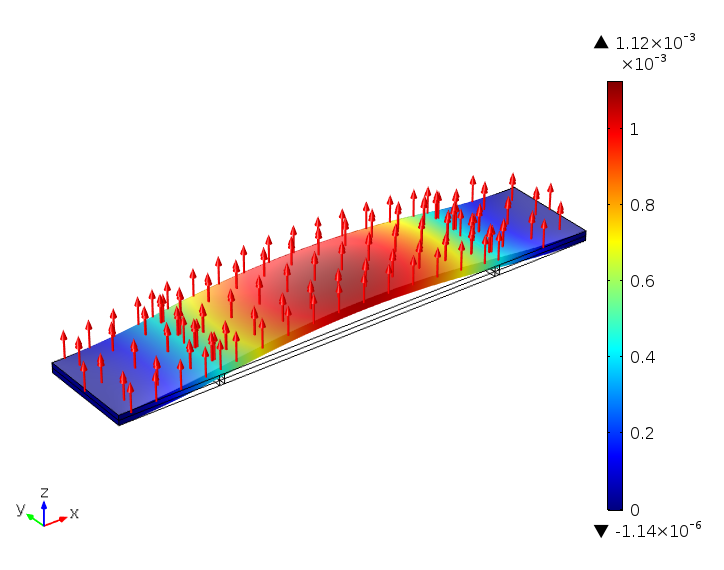
对于两端固定的单晶悬臂,改变极化方向也能改善总位移。
模拟压电薄膜 MEMS 器件
我们最后一个例子特别有意思。不使用技巧,但实际上不会有任何位移,因为整个周长是固定的,因此,没有任何空间让组件发挥作用。应用与前面例子中的相同技巧,整个周边固定的薄膜可以产生极大的位移。这里所示的模拟可以用作 MEMS 器件,例如补偿光学像差(特别是球面像差和像散)。
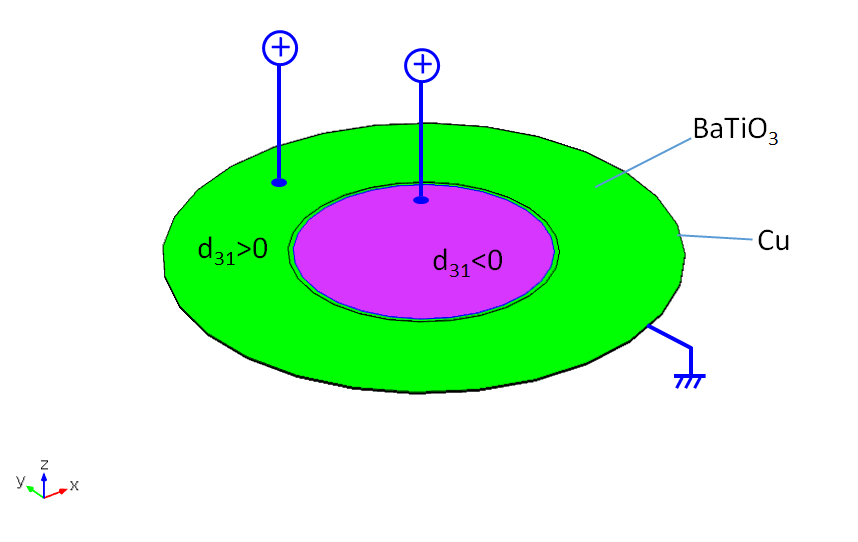
整个周长固定的薄膜 MEMS 器件中的替代材料和电压配置。
整个周边固定的薄膜MEMS器件。施加交变电场或极化方向可改善总位移。
从基本模拟到有用的设计技巧
综上,我们复习了一些基本的数学公式和惯例,这对模拟压电材料是有必要的。此外,我们已经向您介绍了进行基本仿真的步骤,您可以使用文中介绍的压电“技巧”模拟更多有趣的应用。
说到诀窍,显著改善位移的秘密是“拐点区”,它是通过改变电场或材料特性产生的。(参考美国专利 7,369,482 获得更多细节和其他例子。) COMSOL Multiphysics 的局部坐标系功能使得为这种具有交替材料取向的系统建立仿真变得非常容易。
如果你喜欢今天的博客文章,一定要看看其他相关的博文,它们可能会激发你的研究兴趣:



评论 (0)