在之前的博客文章中，我们讨论了在 COMSOL Multiphysics 中求解稳态问题的合并解特征。本篇博文，我们将介绍参数化扫描、特征频率、频域和瞬态问题的合并解。此外，我们还将合并解与内置的 with 算子和 at 算子进行了对比。特别的，我们介绍了一个如何使用合并解进行网格收敛性研究示例，用于评估收敛的模是因变量差的平方。
合并参数化扫描的稳态解
假设这样一种情况：我们已经使用 COMSOL Multiphysics 中的“参数化扫描”功能求解了一系列参数问题，并希望比较不同参数的结果与参数基准值的差异。例如，网格收敛性研究，其中单元大小是扫描参数，并将每个网格大小的解与最细化网格的解进行比较。你会怎么做？
为了评估一些模的差异，我们首先需要建立一个合并数据集。如前所述，当“合并”或比较解时，要求我们选择要合并的两个基本数据集：数据1 和数据2。对于参数研究，每个基础数据集包含多个解。因此，我们必须决定是否只将一个或所有参数值与基准解进行比较。例如，在网格细化研究中，我们可以为 data1 选择“全部”，为 data2 选择“一个”。选择“一个”时，COMSOL Multiphysics 将显示一个下拉菜单，我们可以在其中选择基准值。
在下图中，最细化网格的单元大小参数 hn 的值为 16。
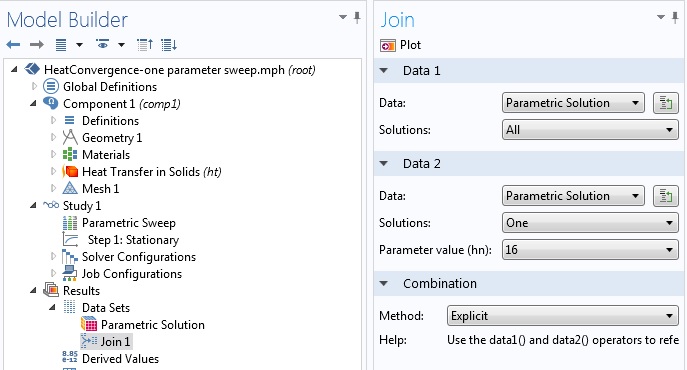
合并一个参数解，将所有参数解与最细化网格中的基准解进行比较。
创建合并数据集后，下一步就是在后处理中使用它。对于上述二维稳态传热问题，考虑温差平方的积分，即温差的 L2-模。要执行空间积分，请至“模型树”中的“结果”栏，右键单击“派生值”，然后选择“表面积分”以获取以下设置窗口：
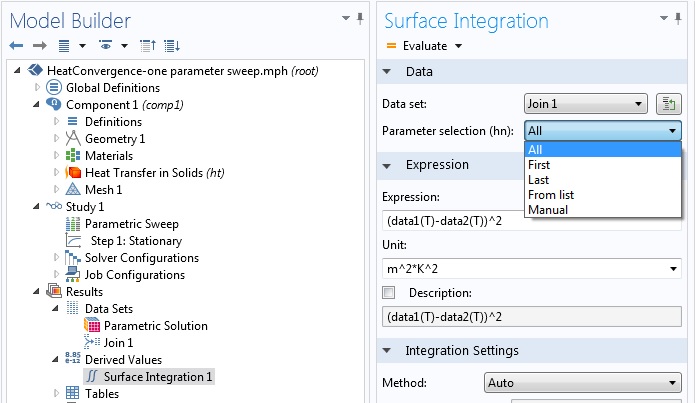
用于计算温差的 L2-模的设置窗口。
如上图所示，我们可以选择在后处理步骤中使用一个，多个或所有参数值。因为在创建合并数据集时，第一个数据集使用了“全部”选项，所以这是可能实现的。通过在“表面积分”设置窗口中选择“全部”，然后单击“计算”，将对最细化网格上的解与所有其他网格之间的 L2 差异进行评估并制成表格。为此，COMSOL 软件将扫描参数的每个值都用作解，并将其用于 data1，而将 hn=16 的解用于 data2。使用“表图”功能，可以获取差异与网格大小的关系图。
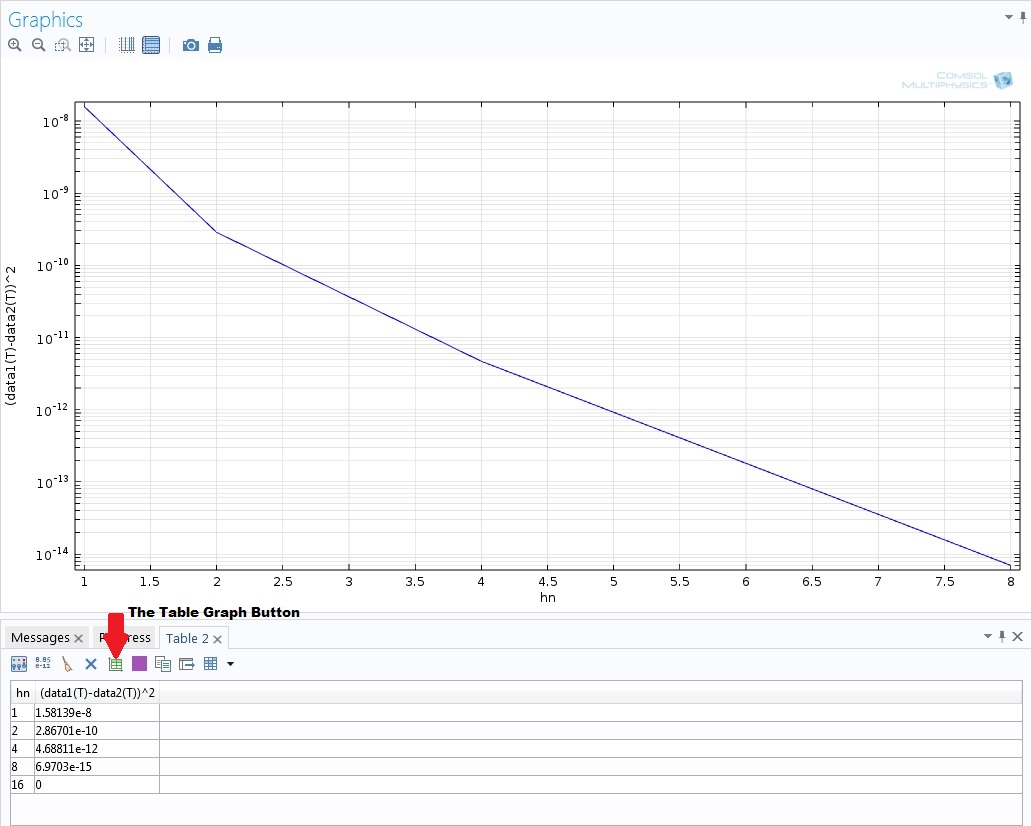
使用指定的合并数据集进行绘图，该数据集将温差的 L2-模与网格大小进行比较。可以使用“表图”按钮立即绘制图形。
多参数扫描
COMSOL Multiphysics 允许我们使用多个参数执行参数化扫描。在多参数扫描中，“扫描”类型有两个选项：“所有组合”和“指定组合”。在第一种情况下，COMSOL 软件执行嵌套型的参数化扫描，其中使用了每种参数组合。在第二种情况下，将构造具有相同索引的参数值的组合，其中所有参数的参数值列表必须具有相同的长度。就合并解而言，该情况与单参数扫描相同。因此，在本示例中，我们将假定扫描类型被设置为“所有组合”，其中参数列表的长度不必相同。
在上述网格收敛性研究中，以传热系数为 5W/(m2K) 的对流热通量作为边界条件。我们使用参数名称 hflux 对该系数进行参数化扫描，以便求解传热系数和网格大小的所有组合。如下图所示：
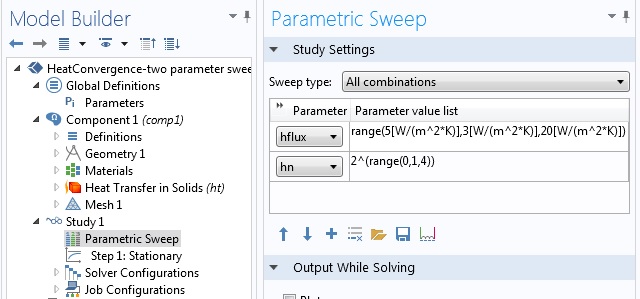
设置多参数扫描。传热系数的参数设置为 5W/(m2K)到 20W/(m2K)，步长为 3W/(m2K)，而网格的参数化方式与前面的情况相同。
创建合并数据集时，COMSOL Multiphysics 会提供参数的矢量化列表，以识别基础解或基准解。在此示例中，我们应选择 hn=16 的组合之一，本例中 hflux=8W/(m2K)：
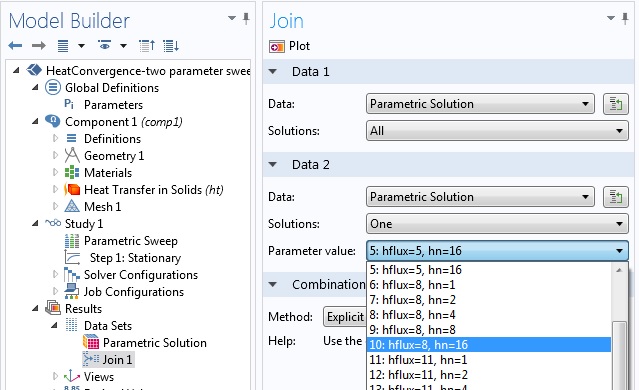
用多参数扫描合并数据集。最细化网格 hn=16 和传热系数 8W/(m2K) 作为基准解。
最后，为了评估 L2 模差异，我们像使用单参数扫描一样使用表面积分。此处的区别在于，我们仅使用 hflux=8W/(m2K) 和网格大小的全部值，而不是使用全部解。出于某些原因，必须考虑所有组合，但是对于网格细化研究，具有相同问题参数（材料属性，边界条件等）的解仅需要比较不同的网格大小。
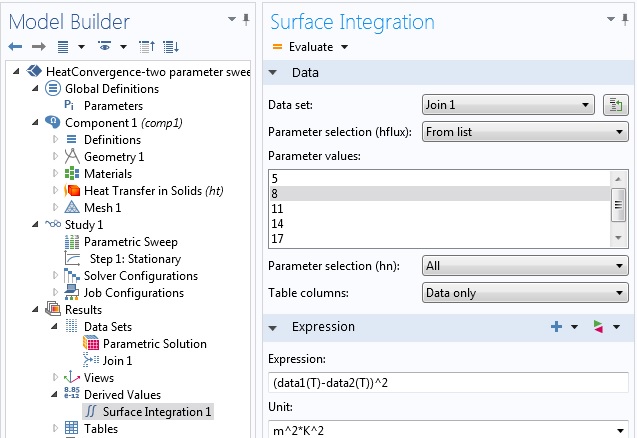
在传热系数值等于 8W/(m2K) 的情况下，为所有网格细化参数指定温差的 L2 模。
如果要为下一个传热系数的值（11W/(m2K)）重复收敛性研究，我们可以返回合并设置窗口，并为 hflux 值和 hn=16 选择参数组合作为第二个基本解。
不同域的解
有时，我们可能在不同的域上定义了基本解。例如，如果在参数化扫描中扫描参数应用到了几何图形的创建过程，则会出现这种情况。在这种情况下，软件仅在用于基本解的域的交集上实现合并数据集。
特征频率、频域和瞬态研究
上述稳态参数研究的方法与在其他研究类型中的工作原理类似。对于特征频率、频域和瞬态研究，参数集将分别由特征频率、频率和时间步形成。
With 算子和 at 算子
对于特征频率、频域和瞬态研究，COMSOL Multiphysics 具有默认算子，可用于处理多个数据集：with 算子适用于上述三种情况，at 算子仅适用于瞬态研究。
with 算子可用于在结果计算时访问解。算子采用两个输入变元，第一个是正整数，它是标识解的索引。值1标识解具有最低特征值、频率或时间值。值2 用于第二最低值，依此类推。第二个输入变元是我们想使用此解计算的表达式。
现在，我们将展示如何在使用 with 算子的同时模拟对合并数据集的操作。主要思路是：当在该操作的“设置”窗口的“数据集”选项中选择的解计算非索引数量时，可以通过使用 with 算子索引来覆盖该选择。例如，我们将使用它来说明如何在特征频率研究中验证振型的正交性。
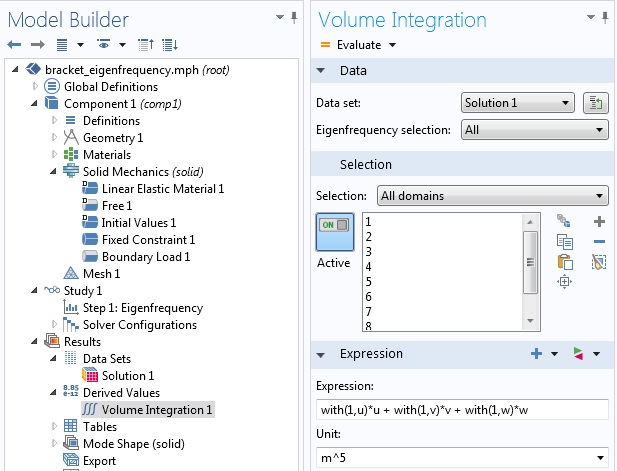
使用 with 算子验证振型的正交性。
上图来自三维固体力学问题的特征频率研究，其中我们评估了六个最低特征值。由于我们在 体积分 设置窗口的“特征频率”选择 中选择了“全部”，因此 COMSOL Multiphysics 会在所有六个特征值下对被积函数“表达式”进行计算。
在每种情况下，当分别在所考虑的当前特征频率值处计算 x-、y- 和 z- 方向上的位移 u、v 和 w 时，在第一特征频率处计算使用 with 算子的索引值。因此，我们希望除了该计算的第一个值以外的所有值都接近于 0。如下表所示：
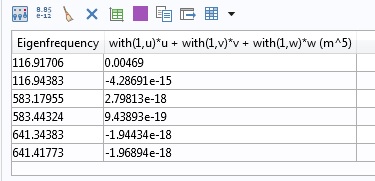
使用 with 算子计算振型的点积。
例如，如果要绘制解中的差异，则同样的思路也适用。在固体力学问题中，我们可以在绘图设置窗口的“表达式”下键入 with（1，v）-with（2，v），以绘制两个最低特征值的 y 位移的差。在有固体力学问题的模型中，如果我们在图上添加了“变形”节点，则 COMSOL 软件允许在变形构型上绘制解。如果想知道使用哪些位移值来获取变形的形状，默认情况下，使用对应于图数据集的解。对于特征频率、频域和瞬态研究，我们可以在“变形设置”窗口中使用 with 算子覆盖该选项。
对于瞬态问题，结果计算时的 at 算子提供了附加功能。与with 算子一样，at 算子采用两个变元，第二个变元与要计算的表达式类似。第一个变元是表示实际时间的正实数。例如，如果在第一个变元中使用1，则表示 t=1（以相关的时间单位），而不是求解的最短时间。如果已经为指定的时间值计算了解，则 COMSOL Multiphysics 将使用计算出的解。否则，它会在求解时使用插值提供的解。
with 和 at 算子能否替代一个合并数据集 来进行特征频率和瞬态分析？答案是，尽管我们可以使用这两个算子对合并数据集重现某些操作，但解合并还具有其他优势。with 和 at 算子只有在相同的数据集当中才有权访问解。考虑这样一种情况：在两种不同的初始条件下，我们已经求解了一个瞬态问题。我们将有两个数据集，分别是解1和解2，每个都包含对应初始条件的所有时间步的解。如果我们想比较基于第一个初始条件的解与基于第二个初始条件的解，则只能使用合并数据集 来执行此操作。此外，合并解提供了一个新的数据集，现在我们可以将其用作另一个合并操作中的基础解。
在某些情况下，使用 with 或 at 算子比创建合并数据集更容易。例如，如果我们要同时使用来自瞬态研究中两个以上时间步的解，则必须形成多个合并数据集。但是，通过使用 with 算子，我们只需键入，例如，with（1，u）+with（2，u）–with（3，u），其中 u 是我们感兴趣的数量，而无需创建多个合并数据集。
结语
在此博客文章中，我们对单个稳态解的合并解的讨论扩展到了参数化扫描、特征频率、频域和瞬态解。对于最后三种类型的研究，我们还展示了如何使用 with 算子和 at 算子进行类似于合并解提供的操作。
如果您对本文内容有任何疑问，欢迎在评论区留言，我们将为您提供专业的技术解答。
评论 (0)