COMSOL 博客

在变分问题中指定边界条件和约束

作者 Temesgen Kindo

2018年 9月 7日

在本博客系列的第一部分中，我们讨论了变分问题，并演示了如何在 COMSOL Multiphysics^® 软件中使用简单的内置边界条件解决它们。今天，我们将讨论更通用的边界条件和约束,并展示如何使用第一部分（皂膜）中的相同变分问题以及同样的数学方法，在 COMSOL^® 软件中实现这些边界条件和约束。

约束分类

对约束进行分类有多种方案。在这里，我们将考虑对计算实现影响最大的那些。

基于相关的几何实体，可以有点（孤立）、分布和全局的约束。例如，一方面，一维问题中的边界条件是在孤立点处的约束。另一方面，应该在每个点都满足的条件是分布式约束。全局约束指定了解的一些标准（通常是一个积分）。例如，指定悬链线的长度或肥皂膜的表面积来提供全局约束。

有些人将术语“逐点约束”用于分布式约束。这里，我们将其与“点约束”做一个明显的区分。点约束在单个点或有限数量的孤立点处执行点约束，这组点没有长度、面积或体积。但是，分布约束在域的每个点上都有效，可以是三维对象的边、面或域的每个点。

另一种分类是等式约束与不等式约束。接触力学中出现了结构力学中常见的不等式约束。装配体中接触对象之间的间隙必须为非负。在化学反应工程中，物质浓度的下界也是不等式。

这些分类也会重叠。例如，我们可以具有分布式的不等式约束和分布式的等式约束，等等。不等式约束在数学上更具挑战性，因此，我们先讨论等式约束，然后在本系列的后面部分中继续讨论前者。

等式约束理论简介

对于微积分问题

\textrm{最小化}\qquad f(\bf{x}), \qquad \textrm{使}\quad g(\mathbf{x})=0

我们可以通过找到关于坐标 \bf{x} 和拉格朗日乘子 \lambda 的扩展目标函数的驻点来求解

\mathcal{L}(x,\lambda) = f(\bf{x}) + \lambda g(\bf{x})

尽管有适当的扩展, 在变分演算中也使用了相同的方法。对于以下问题

\textrm{求函数} u(x) \textrm {的最小值}
E[u(x)] = \int_a^b F(x,u,u^{\prime})dx,

\textrm{ 对于所有 x 满足} g(x,u,u^{\prime})=0 \textrm.

分布式约束 g(x,u,u^{\prime})=0 必须满足域当中的所有点，而不仅仅是某一点。因此，每个点都将会有自己的拉格朗日乘子，使 \lambda 成为一个函数，而不仅仅是一个数字。因此，增广函数如下

(1)

E[u(x),\lambda(x)] = \int_a^b [F(x,u,u’)+\lambda(x)g(x,u,u’)]dx.

在将约束变分问题从一个场 u(x) 转换成不受约束问题的两个场 u(x) 和 \lambda(x) 之后，我们将寻找最优准则。我们可以通过在求解场和拉格朗日乘子场中都做独立的变分，来找到一阶最优准则

\frac{d}{d\epsilon_1}E[u+\epsilon_1 \hat u,\lambda+\epsilon_2 \hat{\lambda}]\bigg|_{(\epsilon_1=0,\epsilon_2=0)} = 0, \quad
\frac{d}{d\epsilon_2}E[u+\epsilon_1 \hat u,\lambda+\epsilon_2 \hat{\lambda}]\bigg|_{(\epsilon_1=0,\epsilon_2=0)} = 0.

对于 F 和 g ，有

\int_a^b \left[\frac{\partial F}{\partial u}\hat{u} + \frac{\partial F}{\partial u’}\hat{u’} + \lambda(\frac{\partial g}{\partial u}\hat{u} + \frac{\partial g}{\partial u’}\hat{u’})\right]dx=0,

\int_a^b \left[\hat{\lambda}(x)g(x,u,u’)\right]dx=0.

这些是我们需要在“弱形式偏微分方程”接口中输入的方程式。首先，我们推导出全局（积分）约束和点（孤立）约束的相应条件。

当有全局约束时

\int_a^bg(x,u,u^{\prime})dx=G,

增广函数是

E[u(x),\lambda] = \int_a^b F(x,u,u^{\prime})dx+\lambda\left[\int_a^b g(x,u,u^{\prime})dx-G\right],

这里， \lambda 是一个数字而不是场。

一阶最优条件是

\int_a^b \left[\frac{\partial F}{\partial u}\hat{u} + \frac{\partial F} {\partial u’}\hat{u’}\right]dx + \lambda\int_a^b \left[\frac{\partial g}{\partial u}\hat{u} + \frac{\partial g}{\partial u’}
\hat{u’}\right]dx=0,

\hat{\lambda}\left[\int_a^b g(x,u,u’)dx-G\right]=0.

最后，使用费米-狄拉克函数的属性，点（孤立）约束 g(x,u,u^{\prime})=0, x=x_o 可以看作全局约束

\int g(x,u,u^{\prime})\delta(x-x_o)dx=0.

同样，我们可以类似地利用费米-狄拉克函数来推导二维和三维中的边以及三维中曲面的约束。

将上述结果插入到全局约束的公式中，得到一阶最优条件

(2)

\int_a^b \left[\frac{\partial F}{\partial u}\hat{u} + \frac{\partial F}{\partial u’}\hat{u’}
\right]dx + \lambda\left[\frac{\partial g}{\partial u}\hat{u} + \frac{\partial g} {\partial u’}
\hat{u’}\right]_{x=x_o}=0,

(3)

\hat{\lambda}g(x_o,u,u^{\prime})=0.

如果我们有多个孤立点约束，则每个点都有一个拉格朗日乘子。拉格朗日乘子将不是一个场，而是一组有限的标量，在每个孤立点上都有一个有效标量。如果我们的分布约束不是施加在整个域上，而是施加在部分域上，则只能在那部分上定义拉格朗日乘子。最后，我们将有一个拉格朗日乘子场。

在 COMSOL Multiphysics^® 中施加约束

现在让我们看看如何在 COMSOL Multiphysics 中施加约束。仍以之前博客文章的皂膜问题为例，但施加了以下边界条件。

u(a) = 2, \quad u^{\prime}(b)=0.

第一个边界条件是可以使用“狄利克雷边界条件”节点指定，但是出于教学原因，我们将使用更通用的约束框架。上面的两个边界条件可以重写为

g(a,u,u^{\prime})=u-2 =0, \quad g(b,u,u^{\prime})=u^{\prime} =0.

我们需要约束方程对 u 和 u^{\prime} 求偏导。

\textrm{At } x=a, \frac{\partial g}{\partial u}=1, \frac{\partial g}{\partial u^{\prime}}=0,

\textrm{At } x=b, \frac{\partial g}{\partial u}=0, \frac{\partial g}{\partial u^{\prime}}=1

最后，我们将在相应的点上将这些作为弱贡献插入。来自的贡献 F 保持与以前相同。

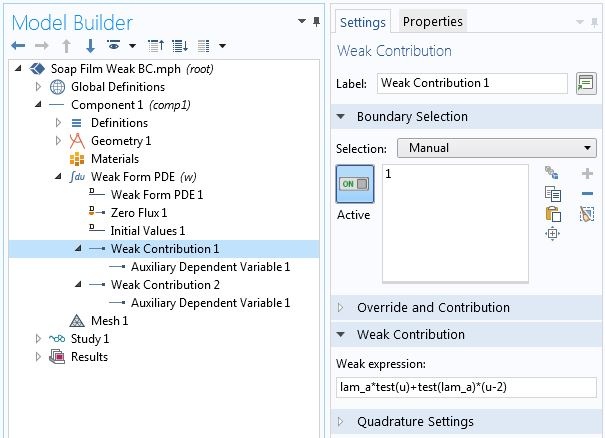
COMSOL软件中的弱贡献设置。

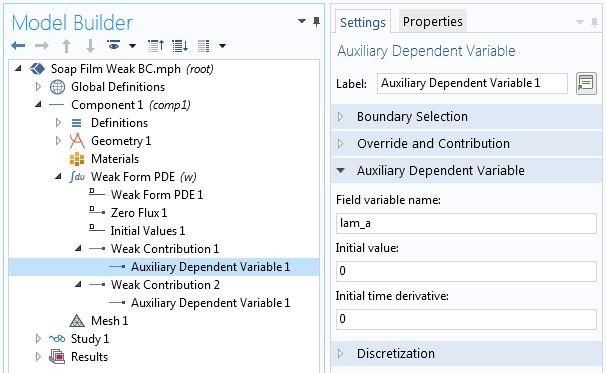
COMSOL软件中的辅助变量设置。

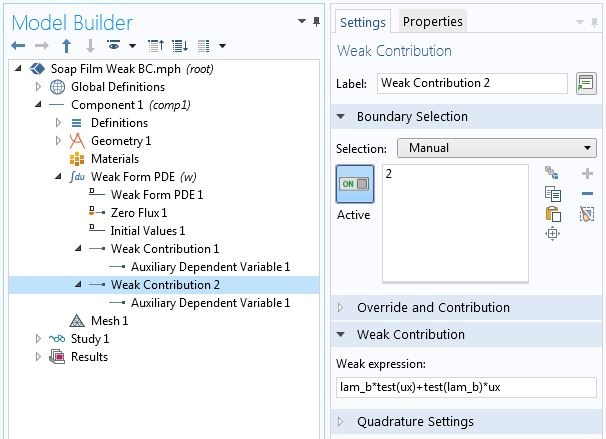
COMSOL软件中的第二个弱贡献设置。
使用点弱贡献指定点约束。

注意，等式3 和等式2 的第二项当中的点贡献都已经被加到“弱贡献”1当中。这里的逻辑是，因为 \hat{u} 和 \hat{\lambda}_a 是独立变分，将包含这些变分的项之和设置为零等同于将包含每个变分的项设置为零。下图显示了具有上述约束的变分问题的数值解。

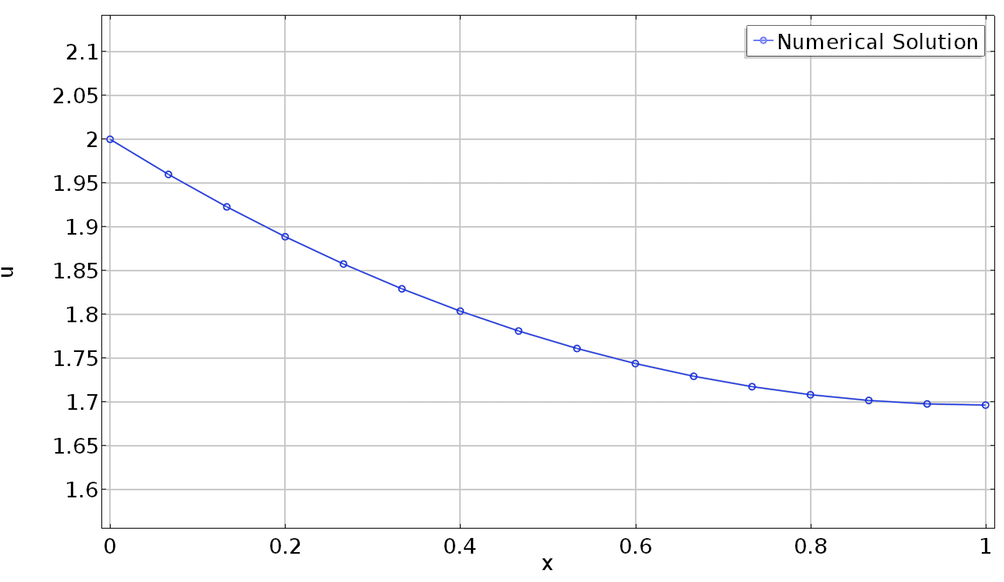
在COMSOL 中执行约束后的结果。
左端半径为 2，右端半径为零的解。

在理论部分，我们讨论了不同类型的约束。下表总结了软件中的推荐位置，这些位置指定了约束的贡献，并根据约束的类型定义了未知数（拉格朗日乘子）。

约束类型	例子	约束贡献包含 \hat{\lambda}	约束贡献包含 \lambda	在哪里定义 \lambda
分布式约束	对材料行为的约束解的上限或下限二维和三维问题中的边界条件	弱贡献	弱贡献	辅助因变量弱贡献下的属性
全局（积分）约束	边长物体重量表面平均位移（温度）	弱贡献	“全局方程”节点	“全局方程”节点
孤立点约束	一维边界条件约束在孤立的内部点上	弱贡献	弱贡献	辅助因变量弱贡献下的属性

指定通量（力）

接下来，我们讨论指定约束条件。为此，我们引入了未知的拉格朗日乘子。在许多物理问题中，拉格朗日乘子是增强约束所必需的反作用力或通量。如果知道作用力或通量而不是约束，如何指定呢？

我们需要回到要最小化的函数并重新计算，包括力（通量）。例如，对于结构力学中的边界载荷，会由于载荷而增加虚拟功。在COMSOL Multiphysics接口中输入的表达式类似于我们对约束所做的事情。用已知的力（通量）代替了拉格朗日乘子，我们不需要拉格朗日乘子作为辅助变量。结果是，包含拉格朗日乘子变化的项消失了。

阅读之前的博客文章，了解有关如何使用弱贡献>添加点载荷（源）的更多信息。

将约束添加到不在几何序列中的点

有时，我们希望向域中未在几何序列中显式插入（或通过曲线的交点创建）的点添加约束。如上例所示，我们无法选择点并将其与点弱贡献关联。但是，我们可以添加全局弱贡献，并使用域探针来引用解及其变体。

例如，对于两端支撑的悬链线。每单位长度重量均匀的电缆的变分问题与轴对称皂膜问题相同。因此，我们将使用相同的 COMSOL 模型。另外，我们希望限制中心高度 u 为 1.95，而无需在几何序列中添加点节点。首先，我们为增加了一个域点探针。探针的名称命名为 ppb1 。对应于(等式1) 的弱贡献为 lam_c * test（comp1.ppb1)，其中 lam_c 是新的拉格朗日乘子。如下面截图所示，我们在全局“弱贡献”节点中输入此贡献。与显式定义的几何实体上的弱贡献相反，此节点不允许创建辅助变量。但是，我们可以添加一个全局方程 节点，在其中可以定义拉格朗日乘子并指定约束。

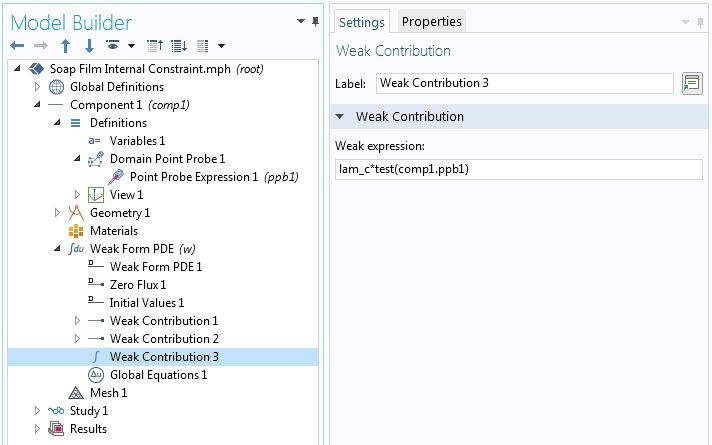
COMSOL软件中的第三个弱贡献设置。

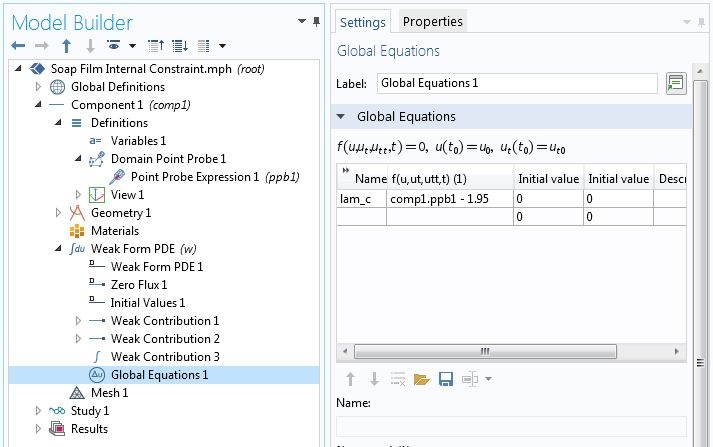
使用COMSOL Multiphysics对不在几何中的点添加约束的演示。
为不在几何图形中的点添加约束。

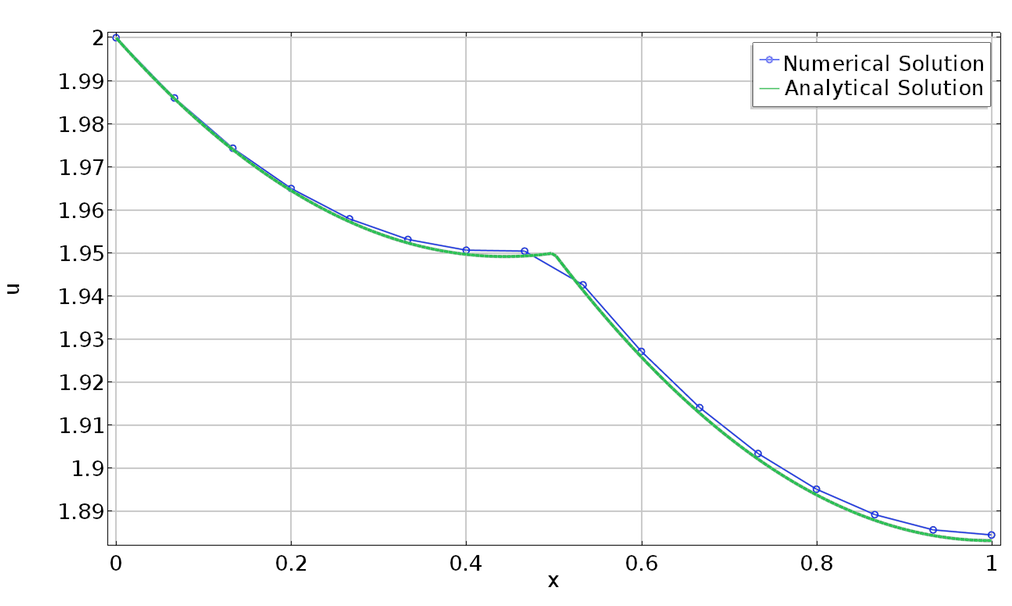
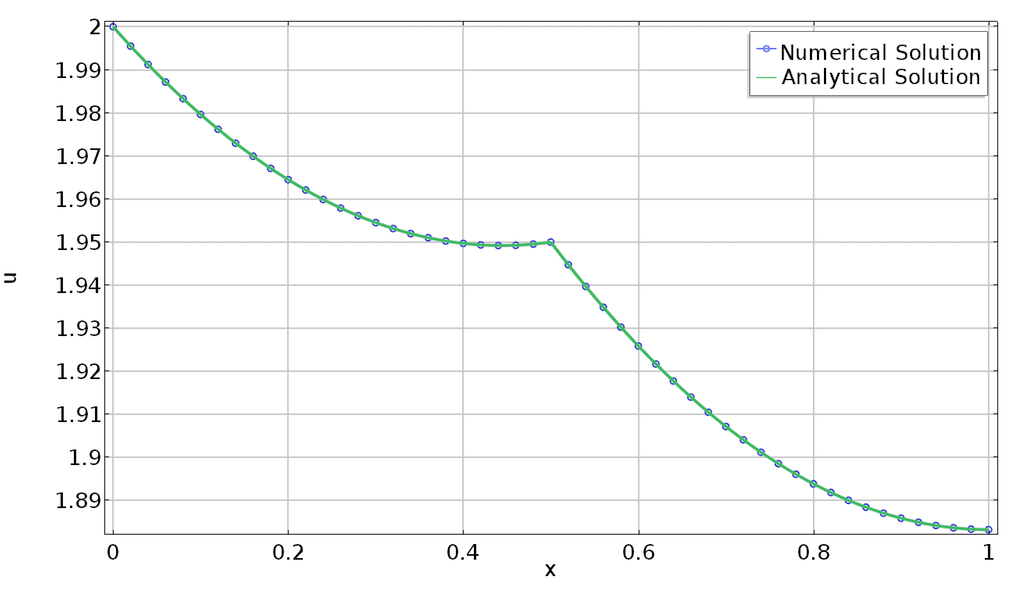
下图显示了包含该约束的解。在网格节点处添加了圆。左图显示了中心点没有与之关联的网格节点的情况。这样，仅近似满足该约束。在右图中，我们可以看到在更细的网格上解的情况，网格剖分器在想要施加约束的地方添加了节点。在此，严格满足约束条件。

验证不在几何序列中的点的内部约束。绘图中未保留纵横比。

我们还可以使用类似的策略来增加点载荷（源），以解决诸如结构力学、传热或化学传递等问题。如前所述，这些负载在数学上对应于拉格朗日乘子。如果我们知道拉格朗日乘子，则不添加全局方程式。相反，我们只有弱贡献，并且代替上面的 lam_c，我们键入了施加的机械、热、化学或其他类型的载荷。

敬请关注！

到目前为止，在本博客系列文章中，我们已经展示了如何使用“弱形式偏微分方程”接口解决变分问题以及如何包含等式约束。

约束在数值解中引入了额外的复杂性，最主要的是，它们导致了鞍点问题，并且拉格朗日乘子实施破坏了刚度矩阵的正定性。对于非线性约束，在非线性迭代期间会出现存在奇异矩阵的危险，尤其是在全局和分布式约束中。

在本系列博客的下一部分内容中，我们将介绍求解这些问题的数值策略。在使用等式约束讨论了这些策略之后，将在后续中讨论不等式约束。

查看“变分问题和约束”系列博客的更多博客文章

博客分类

Yanbin He

2021-02-21

This should be helpful for understanding the Dirichlet BCs. Can you show some examples about imposing continuity BCs?

浏览 COMSOL 博客

在变分问题中指定边界条件和约束