
1961 年,R. Fitzhugh (参考文献1) 和 J. Nagumo 提出了一个模型,用于模拟在生物体的可兴奋细胞中观察到的电流信号。这个被称为数学神经科学的 FitzHugh-Nagumo (FN) 模型,是 Hodgkin-Huxley (HH) 模型(参考文献2)的简化版本,该模型显示了神经元中的尖峰电流。在今天的博客文章中,我们将通过在 COMSOL Multiphysics® 软件中构建交互式 App 来检查 FN 模型的动力学。
神经细胞的动作电位
神经细胞通过脂质双层膜与细胞外区域分开。当细胞不传导信号时,跨膜的电位差约为 -70mV。这种差异被称为细胞的静息电位。细胞内部的矿物质离子,如钠和钾,以及带负电的蛋白质离子,维持静息电位。当细胞受到外部刺激时,它的电位会急剧上升到一个正值,这个过程被称为去极化。然后再次下降到静息电位,称为复极化。
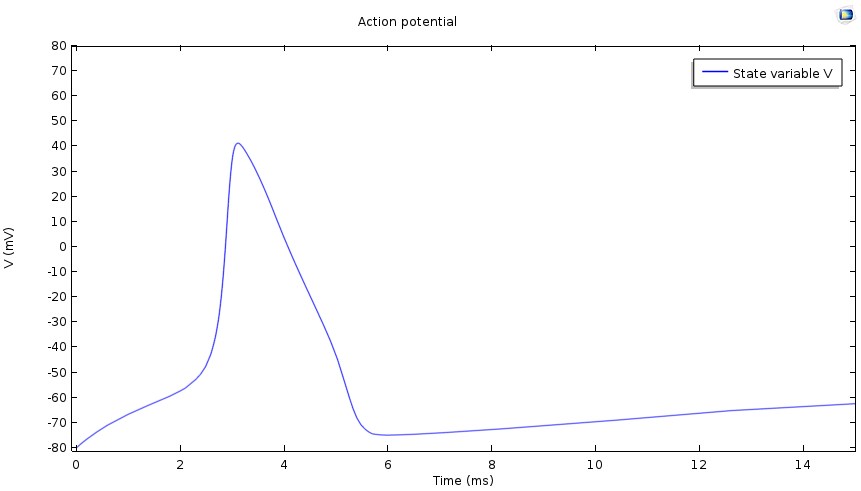
细胞的动作电位图。
在一个示例中,细胞外区域的静止钠离子浓度比细胞内的高得多。这种膜包含有选择性地允许离子通过它们的门控通道。当细胞受到刺激时,钠通道打开,钠离子涌入细胞。这种钠“电流”提高了细胞的电位,导致去极化。然而,由于通道门是电压驱动的,钠通道门会在一段时间后关闭。然后钾通道打开,钾离子流出,导致细胞复极化。
Hodgkin 和 Huxley 通过数学方程解释了产生这种动作电位的机理 (参考文献 2)。虽然这在生物现象的数学建模方面取得了巨大的成功,但完整的 Hodgkin-Huxley 模型却相当复杂。另一方面,FitzHugh-Nagumo 模型相对简单,参数较少,只有两个方程。一个是模拟动作电位的量 V,另一个是调制 V 的变量 W。
今天,我们将重点讨论 FN 模型,以后将讨论 HH 模型。
定义 FitzHugh-Nagumo 模型
FN 模型中的两个方程是
和
参数 I 相当于一个激励,a 和 b 是模型的控制参数。由于参数 ε 乘以第二个方程右边的所有项,W 的演化比 V 的演化要慢。FN 模型方程的平衡点是以下方程组的解:
和
零斜率线 V 和零斜率线 W 分别是 V-V^3/3-W + I 和 V+a-bW, 在 V-W 平面的曲线。请注意,零斜率线 V 是 VW 平面上的一条三次曲线,而零斜率线W是一条直线。控制直线 V+a-bW 的斜率的方式是使零线相交于一个点,使它成为系统唯一的平衡点。
参数 I 简单地向上或向下移动零斜率线 V 。因此,改变 I 值调整平衡点的位置,这样不同的 I 值可以使平衡点位于曲线 V-V^3/3-W + I 的左侧、中间或右侧。
FN 模型的动力学机制
为了模拟平衡点位于每个区域时发生的情况,我们可以使用 COMSOL Multiphysics® 基础模块中的全局微分代数方程 接口。
零斜率线 V 在下图中用绿色表示。在该零线上方 \frac{dV} {dt}<0,而在其下方 dV/dt 为正值。零斜率线 W 用红色表示,在这条直线右边区域,\frac{dW}{dt}>0,在左边区域,\frac{dW}{dt}<0。
如果平衡点在零斜率线 V 的右侧区域 3,让我们看看会发生什么。当表示时间的t等于零时,V 和 W 也都是零。在这种情况下,\frac{dV} {dt} 和 \frac{dW}{dt} 在起始点和附近都是正的,因此它们都随着时间的推移而变化。但由于 V 的演化速度比 W 快,因此 V 迅速增长,而 W 几乎保持不变。在图中,我们可以看到这导致了 V-W 曲线的近水平部分。
随着曲线接近零斜率线 V,V 的变化速率变慢,W 变得更加突出。由于 \frac{dW}{dt} 仍然为正,W 必须增加,曲线向上移动。然后,平衡点吸引这条曲线,演化在平衡点处结束。
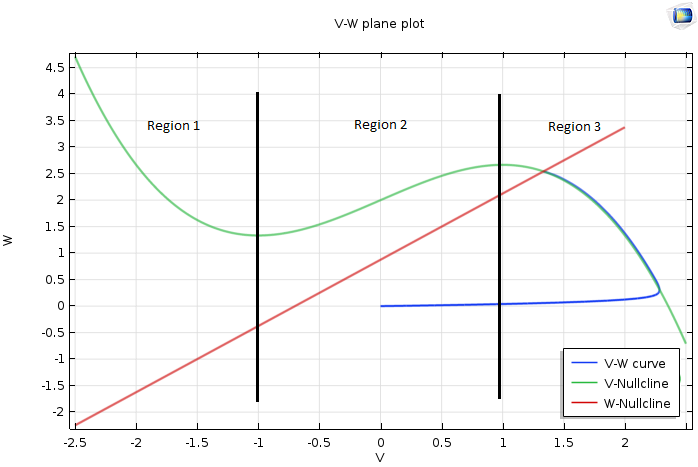
当固定点在零率线 V 的右侧时,VW 平面的绘图。
如果平衡点在中间,即区域 2,那么我们到目前为止讨论的内容都适用。不同之处在于,一旦曲线超出零斜率线 V 的右拐点,\frac{dV}{dt} 变为负值,V 迅速衰减。向左移动时,曲线从右向左穿过红色零斜率线。从这一点开始,当 V 和 W 都减小时,V 的演变占主导地位,曲线再次变为水平。
这一直持续到曲线碰到 V 零斜率线的左侧部分。曲线开始环绕零斜率线 V 并开始缓慢下降。当它接触到零斜率线 V 的左膝时,它会迅速向零斜率线 V 的右侧移动。请注意,这种运动永远不会到达平衡点,因此会不断重复,我们可以在下图中看到。
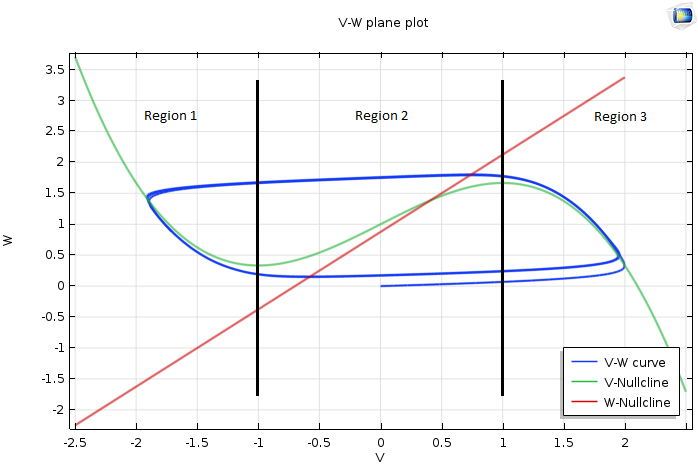
当不动点在零斜 率线 V 的中间区域时 VW 平面 的绘图。
下面,就剩下最后一种情况需要讨论了——当平衡点在零斜率线 V 的左侧区域1时。结果应该如下图所示。请注意,我们前面进行的分析将继续进行。
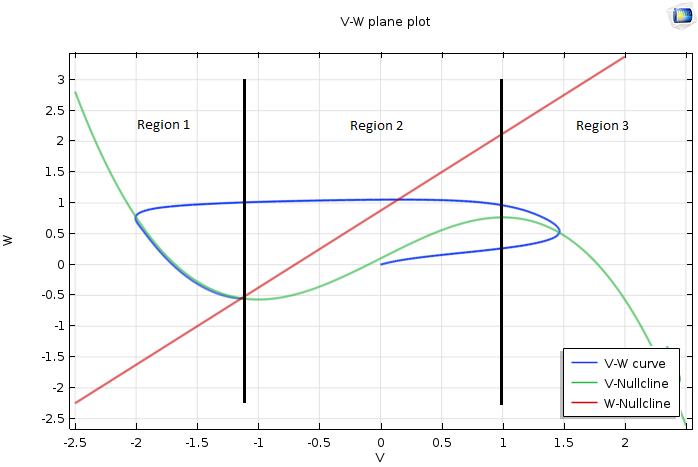
当平衡点在零斜 率线 V 的左侧时,VW 平面的 绘图。
使用 App 开发器模拟 FN 模型
为了探索上述 FN 模型的丰富动态,我们需要在不改变底层模型的情况下反复更改各种输入。因此,需要一个允许我们轻松更改模型参数、执行仿真和分析新结果的用户界面,而不需要导航模型开发器的树结构来执行这些不同的操作。
要完成这一点,我们可以求助于 App 开发器。这个平台允许我们创建一个易于使用的仿真 App,来显示模型的基本参数,而将其他复杂的程序隐藏在后台。有了这个 App,我们可以通过友好的用户界面快速改变参数,并使用静态图形和动画研究结果。这个 App 也可以在教学时使学生很容易的理解 FN 模型的动态,而不必创建模型。
App 的模型参数 部分显示了 FN 模型的重要参数,a、b、 ε 和 I。图形面板显示了各种用户感兴趣的量,例如 V 和 W 的波形。右上角显示了相平面图以及 V-和 W-零斜率线。从这个图中很容易识别平衡点的位置。模拟完成后,我们可以通过从功能区工具栏中选择动画选项来为时间轨迹绘制动画。选择“仿真报告” 按钮,可以需要获得仿真参数和结果的摘要。
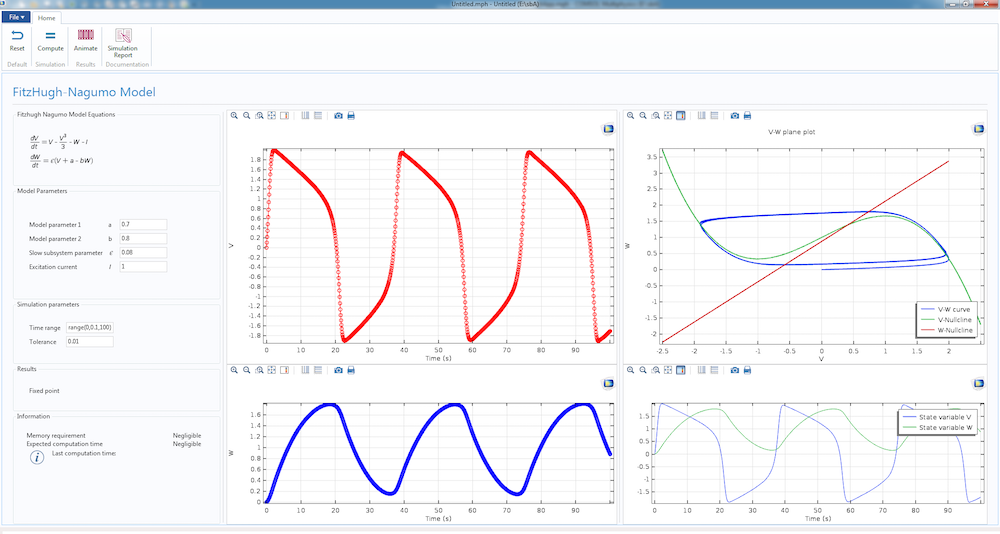
此仿真 App 显示了当不动点位于区域 2 时,FitzHugh-Nagumo 模型的动态。
我们可以很容易地用我们的 App 重现上一节描述的案例。例如,上面的图像显示了平衡点位于区域2 时的情况。我们可以轻松地将平衡点移动到区域1 或区域3,分别设置当前值为 0.1 或 2.5。需要注意的是,App 中的其他参数也可以改变,用来查看是否会出现其他有趣的趋势。
在这里介绍的 App 只是使用 App 开发器可以创建的 App 的一个示例。你的 App 设计,从布局到包含的参数,都由你决定。App 开发器的灵活性使您能够根据需要添加尽可能多的复杂性,这在一定程度上要归功于针对 Java 方法的方法编辑器。在后续的博文中,我们将创建一个 App 来说明更复杂的 HH 模型的动态。请继续关注!
参考文献
- FitzHugh R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophysical Journal. 1961;1(6):445-466.
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology. 1952;117(4):500-544.
使用 App 开发器的更多参考文献
- 在这篇博文用 COMSOL® 应用程序实现弱表单中,你可以看到如何将基于方程的建模和 App 结合起来
- 要了解如何创建建自己的 App,请查看我们的 App 开发器视频系列介绍
Oracle 和 Java 是 Oracle 和/或其附属公司的注册商标。






评论 (0)