
使用 COMSOL Multiphysics® 软件的附加产品 RF 模块中的远场域 功能,可以测量任何散射体或天线的远场响应。具体来说,就是使用 COMSOL 中的有限元-边界元(FEM-BEM)耦合方法,可以最大程度的还原实验设置,例如,用于求解电磁兼容/电磁干扰(EMI/EMC)问题的天线增益测量或电路板的发射或抗扰度测试。使用这种耦合方法,也可以研究微带贴片天线模型周围无限自由空间的波传播。在这篇博客中,我们将深入探讨使用 FEM-BEM 耦合方法解决的一个实际应用:用于 LoS 通信的发射器和接收器天线仿真。
LoS 通信
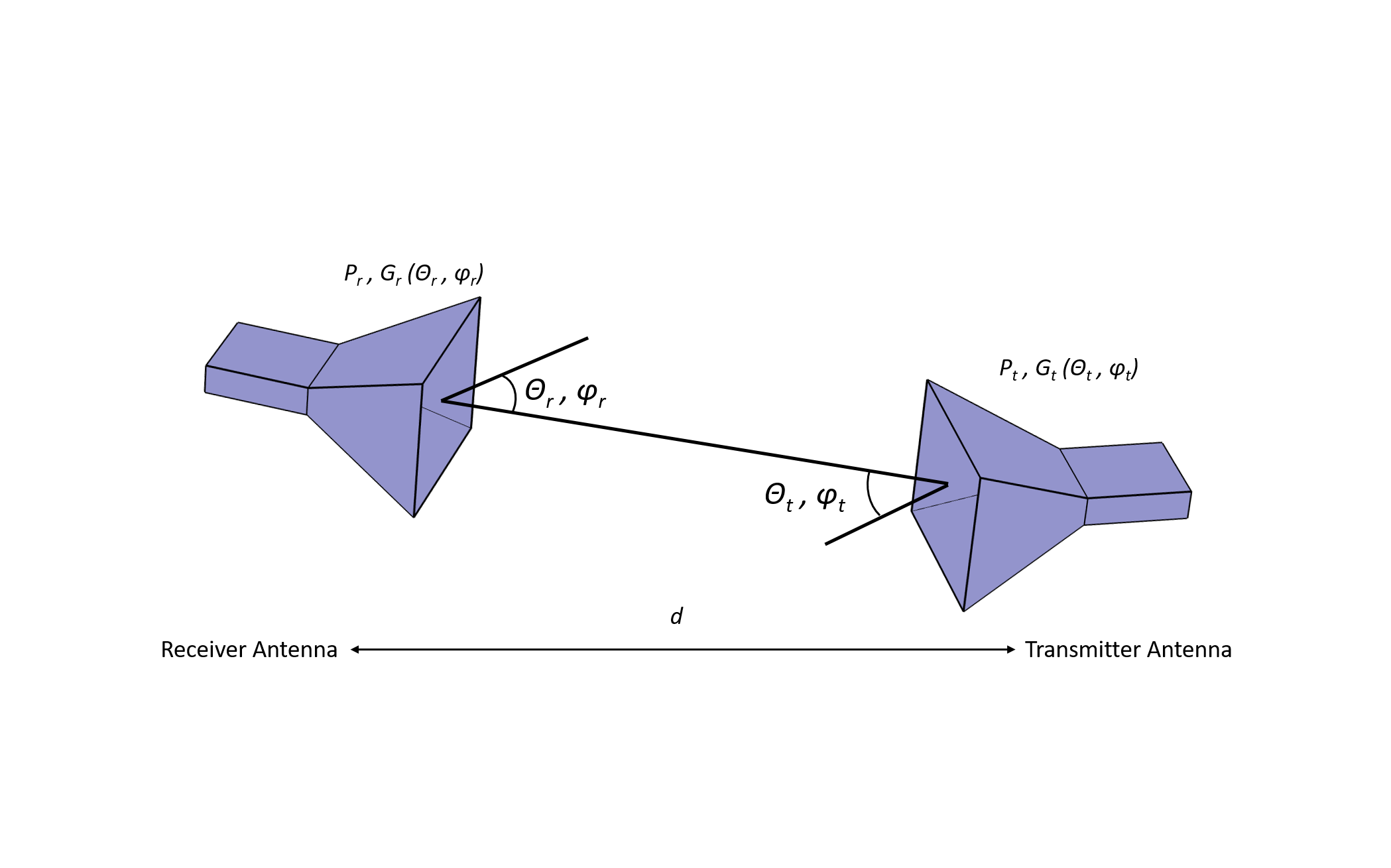
要理解 LoS 通信,知道天线是如何接收功率的很重要。这可以通过著名的 Friis 传输方程(单位:dB)获知:
{P}_\text{r} = \text{P}_\text{t} + \text{G}_\text{t}(\theta_t, \phi_\text{t}) + \text {G}_\text{r} (\theta_\text{r}, \phi_\text{r}) + \text {Path Loss} \quad \quad \quad (1)
式中,\text {P}_\text{r} 是发射功率;\text{P}_\text{t} 是接收功率;\text{G}_\text{t} (\theta_t, \phi_\text{t}) 和 \text {G}_\text {r} (\theta_\text{r}, \phi_\text{r}) 分别是发射天线和接收天线的增益; \text {Path Loss}(单位:dB)由方程(2)给出
其中,{\lambda} 是工作波长,d 是天线之间的距离,这个距离通常代表菲涅尔区域中天线之间的最短距离(这个区域是天线之间形成的一个椭圆区域,不包含任何可能干扰信号传输的物理障碍物)。
对方程(1)进行变形得到如下所示的方程(3),这样,我们可以将方程(3)等号右边的项与通过仿真得到的 S 参数进行比较,
\text{ -P}_\text{t} = \text{G}_\text{t}
(\theta_\text{t} , \phi_\text{t}) + \text{G}_\text{r}(\theta_\text{r},\phi_\text{r}) + \text {Path Loss} \quad \quad \quad (3)
式中,等号左边代表 S21(单位:dB)。
发射器和接收器天线仿真
从 Friis 方程中 \text {P}_\text{r} 可以很好地理解, 可以通过最小化路径损耗来实现最大化,因为通常路径损耗随着工作频率和/或发射器和接收器天线之间距离的增加而增加。如图2 所示,在有限元域中对发射器和接收器进行建模,并通过预定义的 FEM-BEM 接口进行耦合。请注意,发射器是一个微带贴片天线,在电磁波,频域3:Tx 和 Rx 天线 (emw3) 接口(也称为 emw3 接口)中,使用集总端口1 电压激励。接收器是一个八木-宇田天线,在emw3 接口中使用无激励的集总端口2。
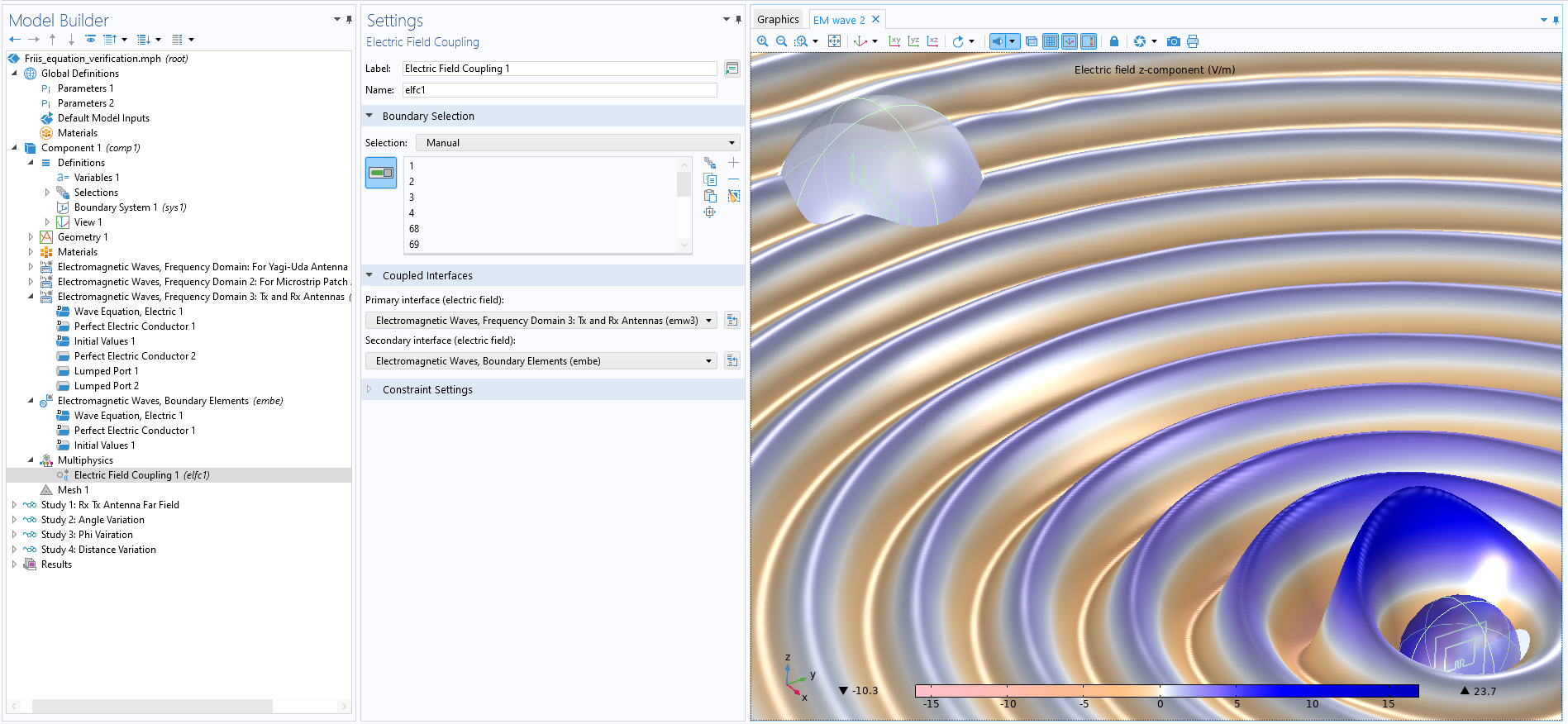
图2. 使用 电场耦合多物理场接口耦合emw3 和 embe 接口。
您还可以借助动画 功能(如下图所示),可视化电磁波从发射器传输到接收器的过程。
电磁波从发射器到接收器的传输。这个仿真使用了 FEM-BEM 耦合功能。
在 Friis 公式中,需要知道两个天线的远场天线增益。这些都可以使用远场域 节点来计算。
- 电磁波,频域:八木-宇田天线(Rx)(emw) 接口 (简称为emw 接口 )
- 电磁波,频域 2:微带贴片天线(Tx)(emw2) 接口(简称为emw2 接口 )
您可以在下面的图片中看到这些接口。
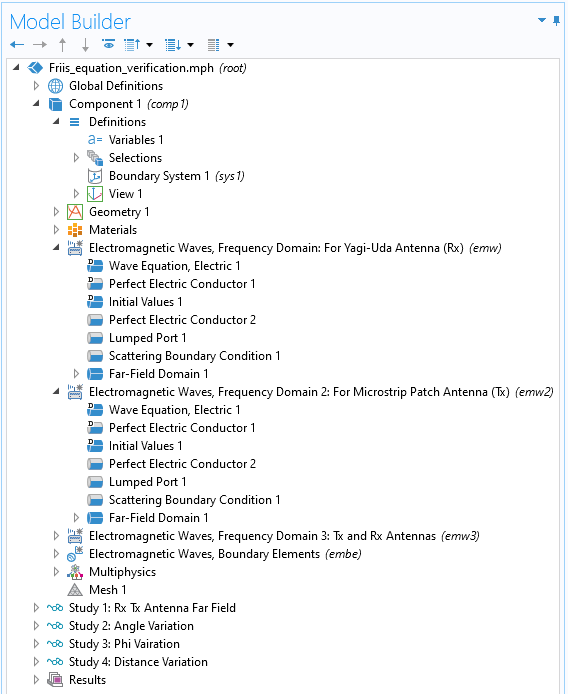
图3.emw 和 emw2 接口被用于计算八木-宇田天线和微带贴片天线的远场增益。
为了进行比较,我们创建了一些变量来定义 Friis 公式(图4),用于计算天线间距增加时与 S 参数有关的接收功率(图5)。
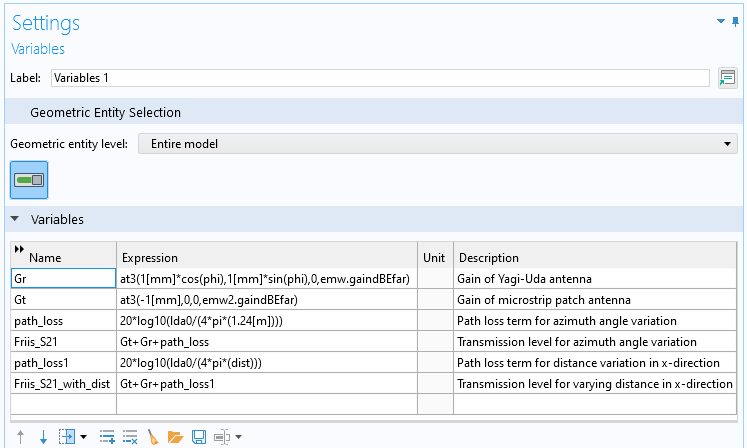
图4.用于定义 Friis 方程的远场表达式。其中,lda0 和 dist 分别代表在自由空间工作的波长和 Rx 和 Tx 天线之间的距离。为了获取通过 phi 角参数定义的特定坐标上的远场增益,使用了预定义的 at3() 函数。
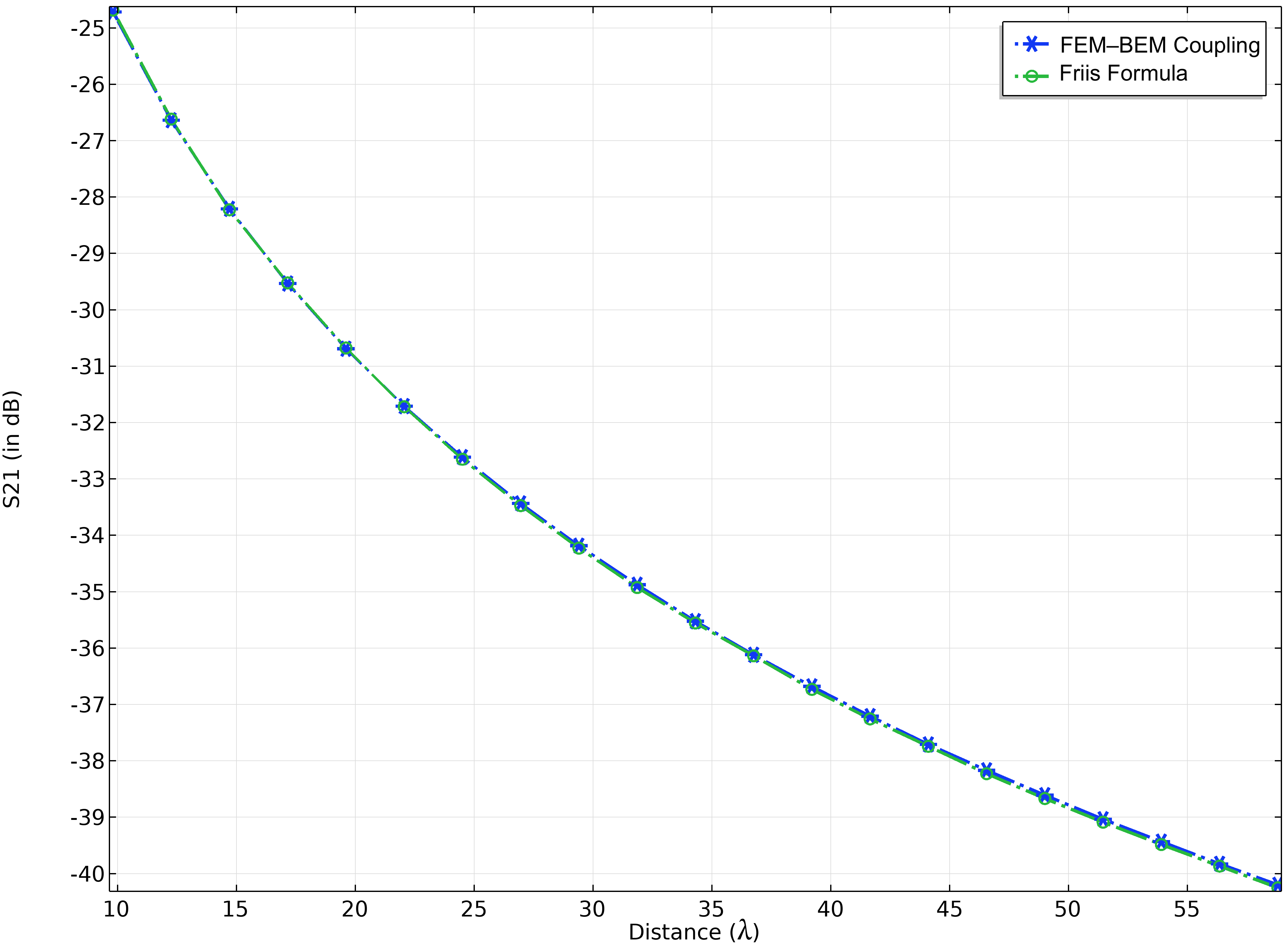
图5. Friis 方程与不同距离的接收功率的比较。
此外,\text{P}_\text{r} 可以通过调整天线辐射模式的主瓣来增大,让我们通过旋转接收器天线的方位角来验证这一点。方位角度可以从 -90o 变化到 90o,换句话说,我们正在模仿天线增益的测量设置。从图6 可以看出,接收到的功率在 0o 时达到最大。这种配置对应于沿 x 轴具有最大增益的两个天线。
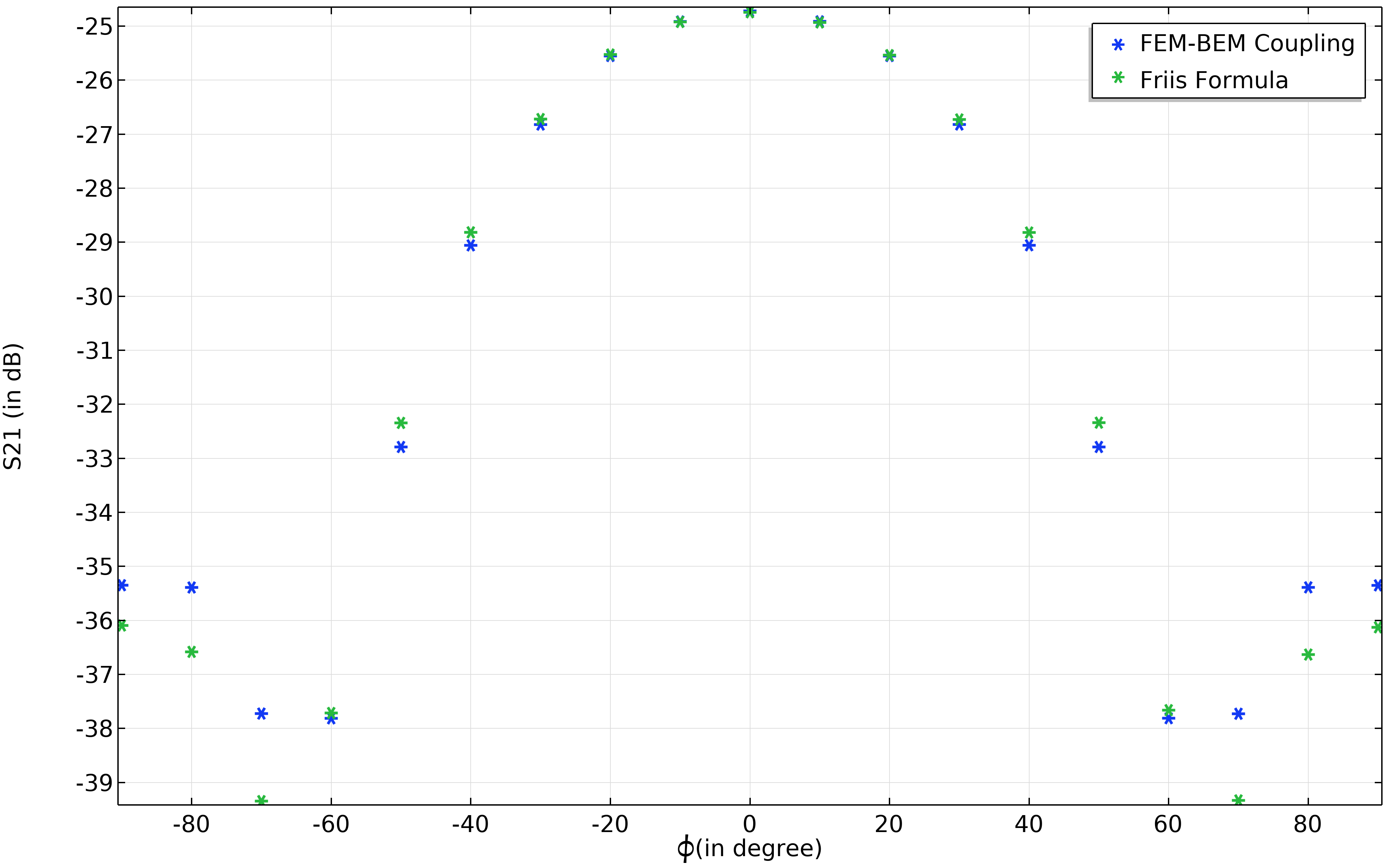
图6. Friis 方程与不同方位角度下的接收功率的比较。
更方便地进行 EMI/EMC 测试
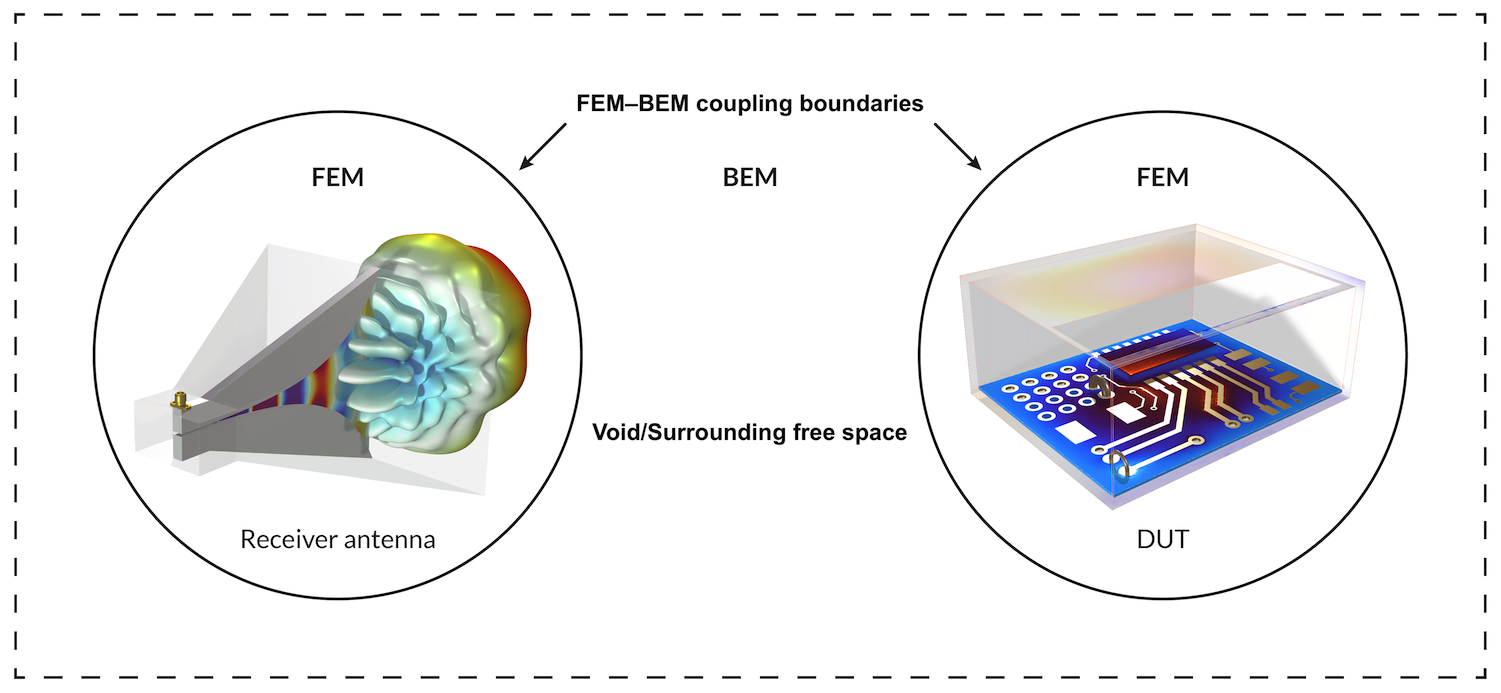
波动光学模块内置的波束包络法克服了对与波长相当尺寸的几何进行非散射电磁建模的障碍,非常适合于波导介质建模。不过,我们也可以使用 FEM-BEM 耦合来模拟散射电磁问题,从而避免处理网格剖分要求或几何尺寸限制的问题。建立 EMI/EMC 测试台模型就是这样一个应用示例。例如,为了执行 RE102 军事标准(高达 18GHz 的频率)的发射测试,被测设备(DUT)和天线之间的距离是 1m。对于频率为 18GHz 的信号,1m 的距离是波长的 60 倍,通过有限元建模这样一个巨大的空间在计算上是非常耗时的。我们可以将被测设备和天线分离成两个有限元域(当然,波长大小相当),并与 BEM 耦合,而不是在单个有限元中建模,如图7所示。天线上检测到的功率可以作为被测设备辐射电磁信号强度的一个衡量标准。
结语
由于网格要求和计算资源限制,电磁仿真会受到限制,FEM-BEM 耦合为更广泛的电磁仿真提供了可行的方法。在研究被测设备的 EMI/EMC 分析中的发射和抗扰度测试应用中,对 Friis 传输方程进行验证使结果更加可靠。
下一步
点击下面的按钮,进入 COMSOL 案例下载页面,尝试自己动手建立验证 Friis 传输方程与 FEM-BEM 耦合的教程模型。
(提示:想要进行更多的建模练习吗?请查看微带贴片天线的 FEM-BEM 耦合教程模型)。






评论 (0)