通过仿真观察图灵模式的发生

被风吹过的沙滩上的沙子，遥远的星状漩涡，热带鱼的绚丽皮肤……我们随处都可以发现大自然中的各种图案。有时，复杂的设计可以从元素与力的一个随机混合中产生。这种 形态发生 的模式生成过程可以在生物和无生命物质中观察到，在某些情况下，可以用 反应扩散方程 来描述。通过化学建模，我们可以模拟图灵模式生成的条件，并且可以看到令人惊奇的视觉效果！

从自催化反应到图灵模式

三次自催化：探索 Gray-Scott 模型，模型教程是使用 COMSOL® 软件的化学反应工程模块开发的，模拟由反应扩散方程控制的自催化 化学反应的效应。下面是一个简单的自催化反应的例子：

A + B → 2B

如果物质 A 和物质 B 发生反应，那么将产生物质 B，直到物质 A被耗尽。随着 B 的相对比例上升而 A 的相对比例下降，混合物将在整个区域范围内扩散。这种运动，或扩散不会是线性的，但也不会完全是随机的。它将创造出被称为图灵模式 的设计，该设计是以艾伦·图灵（Alan Turing）的名字命名的，这位伟大的数学家在 1952 年的论文 The Chemical Basis of Morphogenesis 中描述了这个过程（参考文献1）。

巨型河豚的皮肤，自然界中发现的众多图灵模式之一。图片由 Chiswick Chap 提供，通过Wikimedia Commons 获得许可（CC BY-SA 3.0）。

多稳态反应扩散系统的 Gray-Scott 模型

如果我们把自催化反应-扩散系统变得更加非线性，会发生什么？在20世纪80年代，研究人员 P. Gray 和 S.K. Scott（参考文献2）探讨了一个加速反应的过程。

A + 2B → 3B

Gray 和 Scott 补充说，作为他们系统的一个条件，物质B将随着时间的推移而衰减。他们的研究发现，这些条件将导致反应扩散过程表现出多重稳定性。这意味着该动态过程将达到平衡，其中A和B的数量和分布几乎是稳定的，但这只是暂时的。该系统将继续在稳定性和快速而复杂的空间扩散期之间摇摆不定。这种现象现在以 Gray 和 Scott 的名字命名，其现象已在化学、物理学和生物学中被观察到。

在 COMSOL Multiphysics 中模拟 Gray-Scott 模型

自动催化教程模型可以构建一个 Gray-Scott 模型的仿真。您可以设置反应扩散过程的参数，然后生成其效果的动画。这些操作发生在用户定义的 2D 组件中，该组件描述了具有周期性边界条件的矩形场。该组件基于理想化的连续搅拌釜式反应器 (CSTR)，它假定试剂在进入化学反应器容器时完全混合。反应开始时，加入均匀浓度的物质 A 和物质B，它们在 CSTR 内相互作用。

下面的动画显示了物质 A 和物质 B 的初始浓度以及它们如何随时间变化。请注意，虽然这两种物质是并排呈现的，但实际上它们在同一个域中是挤在一起。反应开始时，混合的 A 和 B 流入 CSTR。流入速率由参数 k 描述，用 10 个等距值对该参数进行扫描。这种扫描使我们能够确定流入速率如何影响反应扩散过程的行为，以及它产生的模式。下面是一个由 0.0609/s 的流入引起的反应的动画：

试剂以 0.0609/s 的速度流入时，物质 A（左）和 B（右）的数量和分布变化。

在这种流入速度下，两种物质的分布迅速演变，直到变化率趋于平稳。随着 k 值沿着参数扫描的移动，反应的行为也会以有趣的方式改变。下图显示了 10 个不同 k 值的演变。

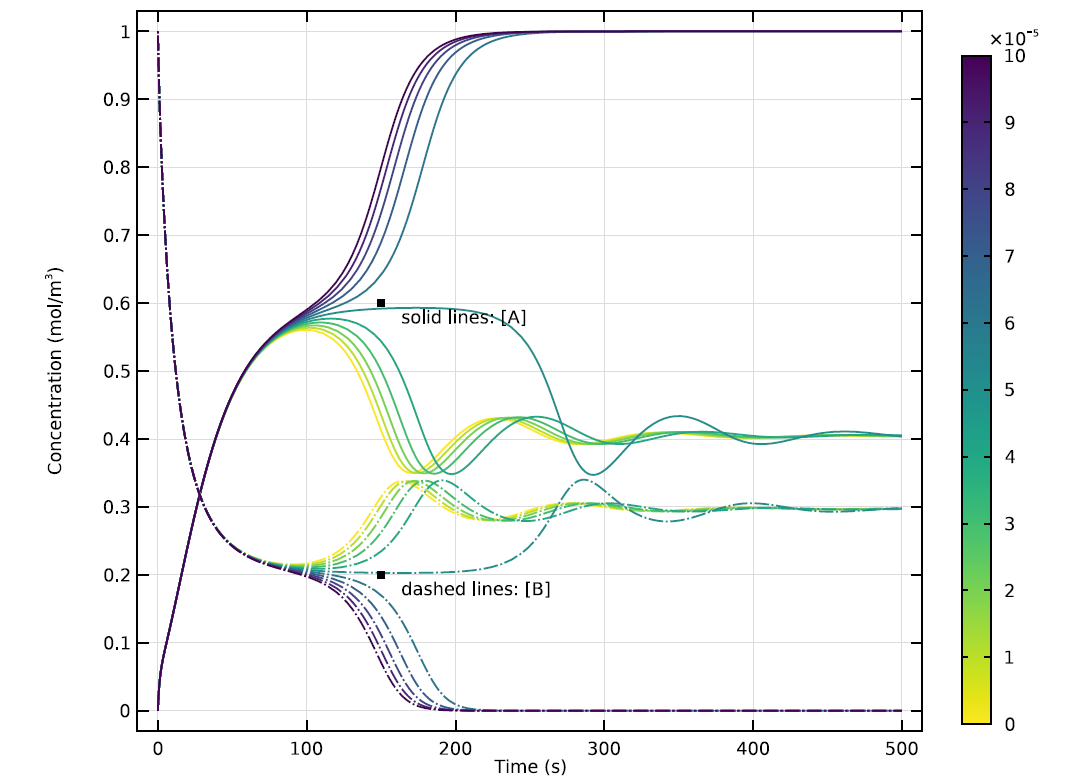
零维 模型中 A 和 B 的浓度随时间的变化，显示了 10 个不同 k值的结果。请注意在某些 k 值处反应波形的明显振荡。

当 k 为 特定值时，A 和 B 的浓度将很快达到稳定平衡。当为其他值时，随着反应朝着 A 和 B 可以共存的条件进行，将出现过渡振荡。这种相对稳定的状态可能远不能统一，但是……

试剂以 0.0611/s 的速度流入，物质 A 和 B 的数量和分布变化的动画。

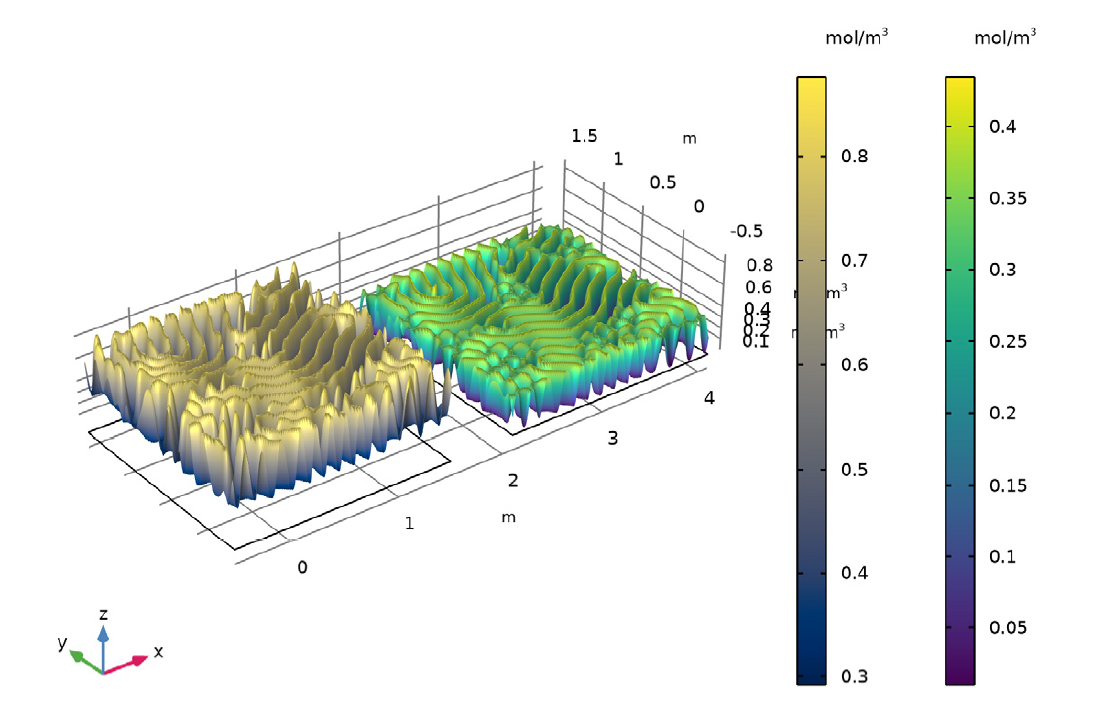
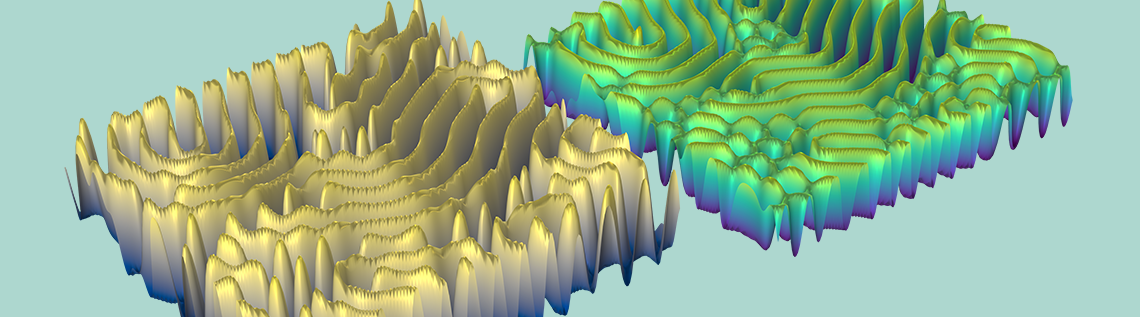
插图显示了 k = 0.06011 时，A 和 B 的最终浓度状态。

如上面的动画和图所示，反应扩散过程可以在合适的条件下生成壮观的图灵模式。

自己动手调试你自己的图灵模式

想不想自己动手探索为宇宙带来秩序的形态发生过程呢？或者，只制作一些很酷的动画？无论哪种方式，您都可以通过下面的按钮下载三次自催化：探索 Gray-Scott 模型的教程模型开始学习，其中包括如何在 COMSOL Multiphysics 软件中运行动画播放器的说明。

参考文献

1. A.M. Turing, “The Chemical Basis of Morphogenesis,” Phil. Trans. R. Soc. Lond. B, vol. 237, pp. 37–72, 1952.
2. P. Gray and S.K. Scott, “Autocatalytic Reactions in the Isothermal Continuous Stirred Tank Reactor, Oscillations and instabilities in the system A + 2B=>3B; B=>C,” Chemical Engineering Science, vol. 39, pp. 1087–1097, 1984.