
当我们敲击由玻璃或金属制成的碗时,会听到清脆的音调而且声音强度会随时间变化而逐渐衰减。理论上,如果不存在阻尼,这种音调将永远不会消失。实际上,碗中产生的动能和弹性势能会通过不同的物理过程转换为其他形式的能量。本篇博客文章中,我们将讨论如何用数值的方法表示阻尼,以及在振动结构中产生阻尼的物理现象。
如何定量计算阻尼?
使用数值的方法描述阻尼有很多种,下面我们将介绍一些最常用的方法。
阻尼最明显的一个表现形式是自由振动时其振幅会产生衰减,例如敲击碗时的声音。振幅的衰减率取决于阻尼的大小。通常,振幅随时间呈指数下降。当一个周期内损失的能量与周期本身的振幅成正比时,就是这种情况。

一个“会唱歌的碗”。图片来源:Sneharamm0han。通过Wikimedia Commons在CC BY-SA 4.0下获得许可。
首先,对于具有黏性阻尼且无外部负载的单自由度(DOF)系统,可以用下面的运动方程描述:
除以质量m后,方程的归一化形式通常写为
这里,\omega_0 是无阻尼的固有频率,\zeta称为阻尼比。
为了使运动为周期性,阻尼比必须限制在以下范围内:0 \le \zeta < 1.该系统中自由振动的幅度将随以下因子衰减
其中,T0是无阻尼振动的周期。
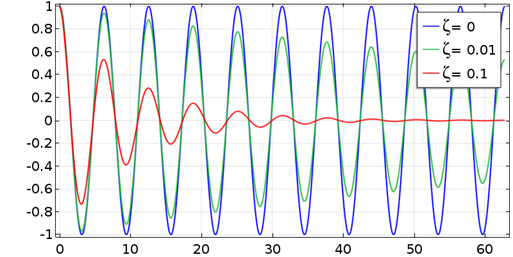
对于三个不同的阻尼比值,自由振动会衰减。
另一种情况,是使用对数衰减,δ 是连续两个峰的振幅之比的对数,
其中,T是周期。
对数衰减量与阻尼比之间的关系为
第三种情况,当结构在接近固有频率下受到谐波激励时,阻尼也较大。当恰好发生共振时,振动振幅会趋于无穷大,除非系统中存在一些阻尼。共振时的实际振幅仅由阻尼量决定。
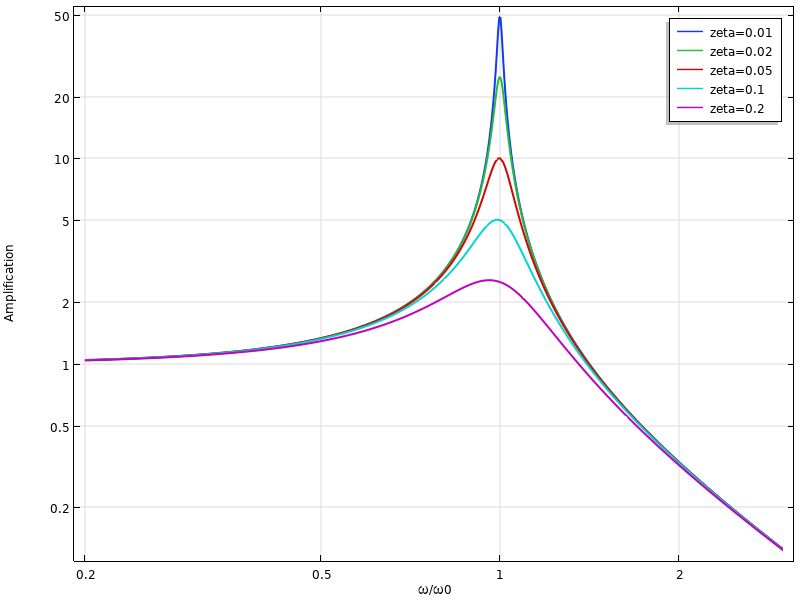
不同频率和阻尼比的单自由度系统的放大图。
在某些系统中,例如谐振器,其目标是获得尽可能大的振幅。这时需要使用另一种常用的阻尼测量方法:品质因子 或Q因子,其定义是共振时的放大倍数。Q 因子与阻尼比有关,可以表示为:
描述阻尼的另一个方法是:假设在施加的力和所产生的位移之间,或在应力和应变之间存在一定的相移。相移仅对稳态谐波振动有意义。如果在一个完整周期内绘制应力与应变的关系图,将得到一个椭圆形的滞回曲线。
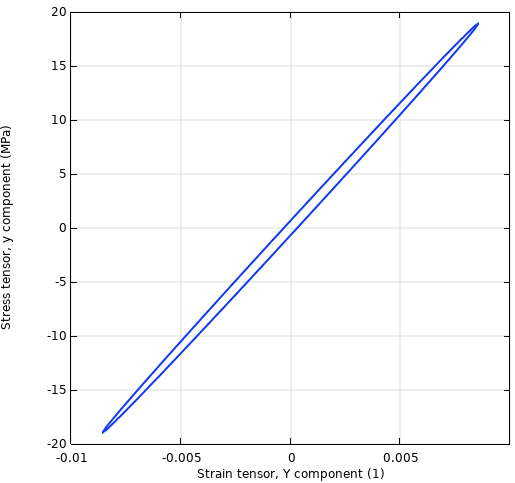
应力与应变的历史图。
假设材料属性是复数值。因此,对于单轴线弹性,复数值应力-应变关系可以写为
这里,将杨氏模量的实部称为存储模量,虚部称为损耗模量。损耗模量通常用损耗因子 η 来描述,因此
此时,E 可以定义为存储模量E’。E 还可以被定义为应力振幅和应变振幅之间的比率,因此
在这种情况下
只有对于高损耗因子值,区别才会很重要。
由损耗因子定义的阻尼,可以用损耗角正切等效度量,损耗角正切 定义为
损耗角δ是应力和应变之间的相移。
由损耗因子定义的阻尼行为与粘性阻尼有所不同。损耗因子阻尼与位移幅值成正比,而黏性阻尼与速度成正比。因此,不能将一个数字直接转换为另一个数字。
下图比较了两种阻尼模型的单自由度系统的响应。可以看出,黏性阻尼在共振处高于损耗因子阻尼,在共振位置以下则低于损耗因子阻尼。
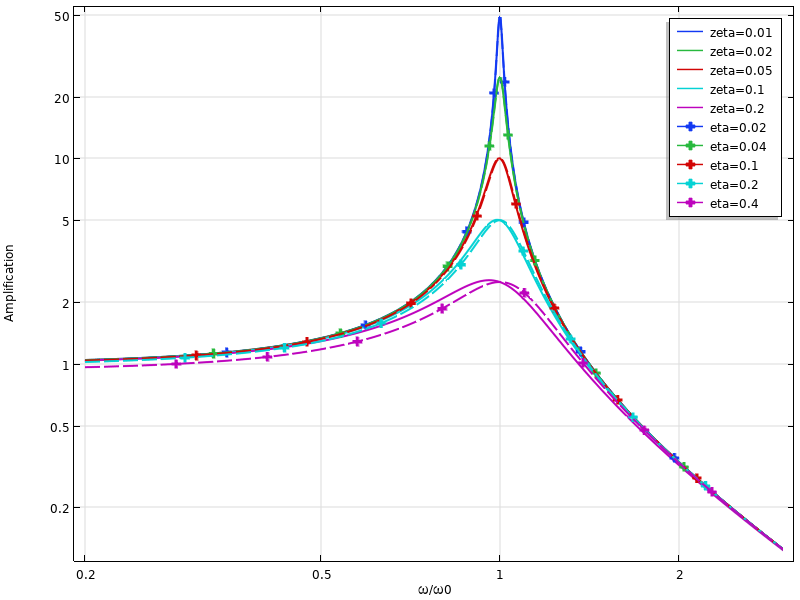
黏性阻尼(实线)和损耗因子阻尼(虚线)的动态响应比较。
通常,在共振频率下考虑阻尼比和损耗因子阻尼之间的转换,此时,\eta \approx 2 \zeta。但是,这仅适用于单个频率。下图为双自由度系统的情况。由图可以看出,阻尼值在第一次共振时已经匹配,很明显在第二次共振时的预测差异很大。
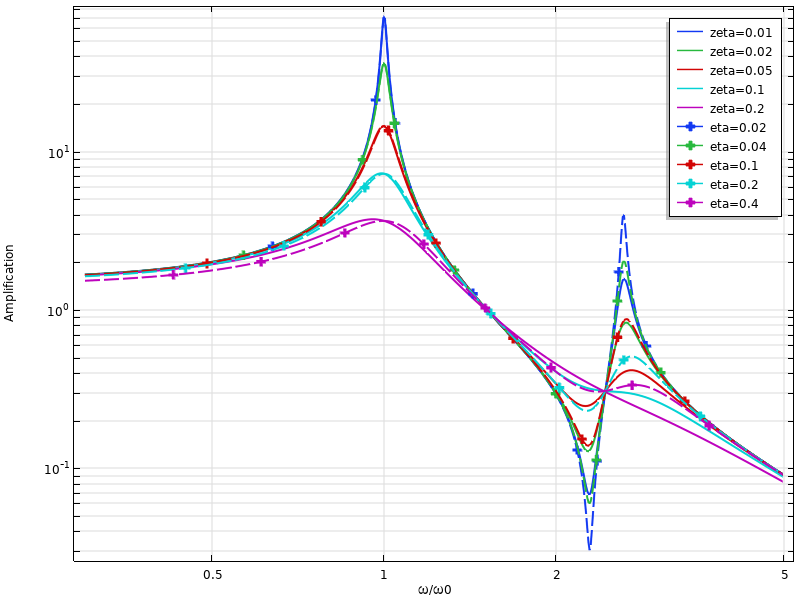
双自由度系统的黏性阻尼和损耗因子阻尼的动态响应比较。
我们还可以根据能量的形式定义损耗因子。可以看出,对于上述材料模型,在一个负载循环过程中耗散的能量为:
其中,\varepsilon_a是应变振幅。
同样,循环中的最大弹性势能为
因此,损耗因子可以用能量表示为
只要可以确定两个能量的值,就可以使用基于耗散能量的描述,而不需要考虑滞回曲线是否是椭圆形。
阻尼的来源
从物理角度来看,阻尼来源有许多可能,大自然总是倾向于寻找耗散能量的方法。
材料内部损失
所有实际材料在受力时都会耗散一些能量,我们可以将其视为一种内部摩擦。如果查看一个完整负载周期的应力-应变曲线,它将不是一条完美的直线,而是更像一个扁的椭圆形。
通常,损耗因子阻尼适合用来表征材料阻尼,因为经验表明,每个周期的能量损耗往往对频率和振幅的依赖性较弱。但是,由于损耗因子阻尼的数学基础是基于复数值,故假设系统为谐波振动。因此,该阻尼模型只能用于频域分析。
材料的损耗因子可能会有很大的差异,具体取决于其组成和来源。下表列出了一些材料损耗因子的粗略估计值。
| 材料 | 损耗因子η |
|---|---|
| 铝 | 0.0001–0.02 |
| 水泥 | 0.02–0.05 |
| 铜 | 0.001–0.05 |
| 玻璃 | 0.0001–0.005 |
| 橡胶 | 0.05–2 |
| 钢 | 0.0001–0.01 |
损耗因子和类似的阻尼描述主要用于材料阻尼的确切物理原理未知或不重要时。在某些材料模型中(例如黏弹性模型),耗散是模型的固有属性。
连接摩擦
通常,结构通过螺栓或铆钉连接。如果连接表面在振动过程中相对滑动,能量就会通过摩擦而耗散。只要摩擦力本身的值在周期内不改变,则每个周期的能量损失或多或少与频率无关。从这个意义上讲,摩擦类似于材料的内部损耗。
螺栓连接是机械工程中很常见的类型。螺栓连接处能量的耗散量可能会很大,具体取决于设计。如果低阻尼对系统影响较大,则应将螺栓紧密隔开并拧紧,以免在连接表面之间产生肉眼可见的滑移。
声音发射
振动表面会置换周围的空气(或其他周围的介质),从而发出声波。这些声波会带走一些能量,从结构的角度来看,这会导致能量损失。

Tonpilz 换能器中的声辐射图。
锚损耗
通常,一个较小的组件会连接至一个较大的结构,而该大结构并不是模拟的一部分。当组件振动时,会在支撑结构中产生一些波并传播出去。这种现象通常称为锚损耗,常见于微机电系统(MEMS)。
热弹性阻尼
即使是没有能量耗散的纯弹性变形,对材料施加应力也会略微改变其温度。局部拉伸导致温度降低,而压缩则会使局部加热。
从根本上讲,这是一个可逆的过程,因此,如果释放压力,温度将回到原始值。但是,通常应力场存在梯度,而温度分布也存在相应的梯度,这将导致从较热区域到较冷区域之间的热通量。当在负载循环的后期消除应力时,温度分布不再与加载引起的温度分布相同。因此,不可能局部返回到原始状态。这成为了一个能量耗散的来源。
当系统在较小的长度尺度和高频振动下工作时,热弹性阻尼效应非常重要。对于 MEMS 谐振器,热弹性阻尼可能会显著降低 Q 因子。
缓冲器
有时,会可以在结构中安装离散阻尼器,例如车轮悬架中的减震器。

减震器。图片由 Avsar Aras 提供。通过 Wikimedia Commons 在 CC BY-SA 3.0 下获得许可。
显然,这些部件对结构中的总阻尼有很大影响,至少对某些振动模式而言会如此。
减震器
在地震活跃地区的土木工程结构中,为了降低建筑物在地震来临时的振动水平,减震器至关重要。这种类型的阻尼器既可以将结构与地基隔离,也可以使能量耗散。

市政建筑的减震器。图片由 Shustov 提供。通过Wikimedia Commons在CC BY-SA 3.0下获得许可。
拓展阅读
阅读本博客的后续文章:



评论 (0)