
经常有用户提出希望能够检查 COMSOL Multiphysics 使用的角系数。它们有多准确?像网格大小、辐射分辨率等这样的已知参数对角系数的准确性有什么影响? COMSOL 中内置了可用于后处理的的算子,这些算子与用于生成表面对表面方程的算子相对应。接下来,我将为大家演示如何计算几何角系数。
关于角系数
传热计算通常需要包括表面对表面辐射,以准确反映真实的情况。模拟表面对表面辐射的数值方法与模拟传导或对流的数值方法有很大不同。后者是基于局部离散化的偏微分方程(PDE),而表面对表面辐射则基于非局部量,即发射和接收辐射的扩散表面之间的角系数。
当表面对表面辐射被激活时,传热接口会创建一系列算子,这些算子会像表面对表面辐射中的辐射变量一样被计算。由于这些算子,有可能获取辐射变量的值,并计算给定几何结构中的几何角系数。
在这篇博客中,我们将解释如何在一个简单的三维几何体中计算已知解析解的几何角系数。
算子
在 COMSOL Multiphysics 5.0 版本中,我们可以使用新的算子访问用于生成表面对表面辐射方程的所有信息。即使是更高级的配置也是如此,如壳体两侧的辐射和具有不同不透明特性的多个光谱带。
我们从最简单的情况开始讨论。假设表面特性像灰色表面。在这种情况下,我们不需要区分光谱带。我们有两个算子,每个面(向上或向下)一个。表达式如下:
radopu(expr_up,expr_down)
radopd(expr_up,expr_down)
这两个算子被设计为在表面对表面辐射活跃的边界上进行计算。假设传热接口标签为 ht,在边界上面的计算点上,ht.radopu(ht.Ju,ht.Jd) 返回表面共辐射 ht.Gm_u。
请注意,ht.Ju 和 ht.Jd 分别定义了边界上面和下面的辐射度。同样,ht.radopd(ht.Ju,ht.Jd) 返回边界下面的表面共辐射, ht.Gm_d。
当考虑到多个光谱带时,一个给定的边界对于一个光谱带来说可能是不透明的,而对另一个光谱带来说是透明的。因此,每个光谱带需要一对算子。它们的作用与灰度表面的算子完全一样,命名如下:
- 第一个光谱带:
radopB1u(expr_up,expr_down)和ht.radopB1d(expr_up,expr_down) - 第二个光谱带:
radopB2u(expr_up,expr_down)和ht.radopB2d(expr_up,expr_down) - 第三个光谱带:
radopB3u(expr_up,expr_down)和ht.radopB3d(expr_up,expr_down) - 等等。
定义角系数
考虑两个漫反射的灰色表面:S1 和 S2。假设辐射只发生在这两个表面的上面。从热学的角度来看,S1 和 S2 之间的角系数,F_{S1-S2},是离开 S1 并被 S2 拦截的漫反射能量与离开 S1 的总漫反射能量的比。
使用上文描述的算子,得到
(1)
=\frac{\int_{S2}{\textrm{radopu}(J_{\textrm{from S1}},0)ds}}{\int_{S1}{J ds}}
为了清楚起见,去掉了 ht. 的前缀。
假设所有表面的辐射率都是相同的值,上述定义可以简化,不再取决于 J。在这个示例中,F_{S1-S2} 只取决于几何配置,不再取决于热配置。我们把这称为几何角系数,以区别于基于热辐射的角系数。
现在有
(2)
{\textrm{radopu}(I_{\textrm{S1}},0)ds}}{\int_{S1}{1 ds}}=\frac{\int_{S2}{\textrm{radopu}
(I_{\textrm{S1}},0)ds}}{S1}
其中,S1 代表表面名称或它的面积,I_{\textrm{S1}} 是表面 S1 的函数指标,当它在 S1 上被计算时返回 1,在其他地方返回 0。
基准案例:两个同心球体
为了适应新的运算符并检查其准确性,我选择了一个简单的配置。该几何体由两个半径为 Rint 和 Rext(Rint < Rext)的同心球组成,如下所示:
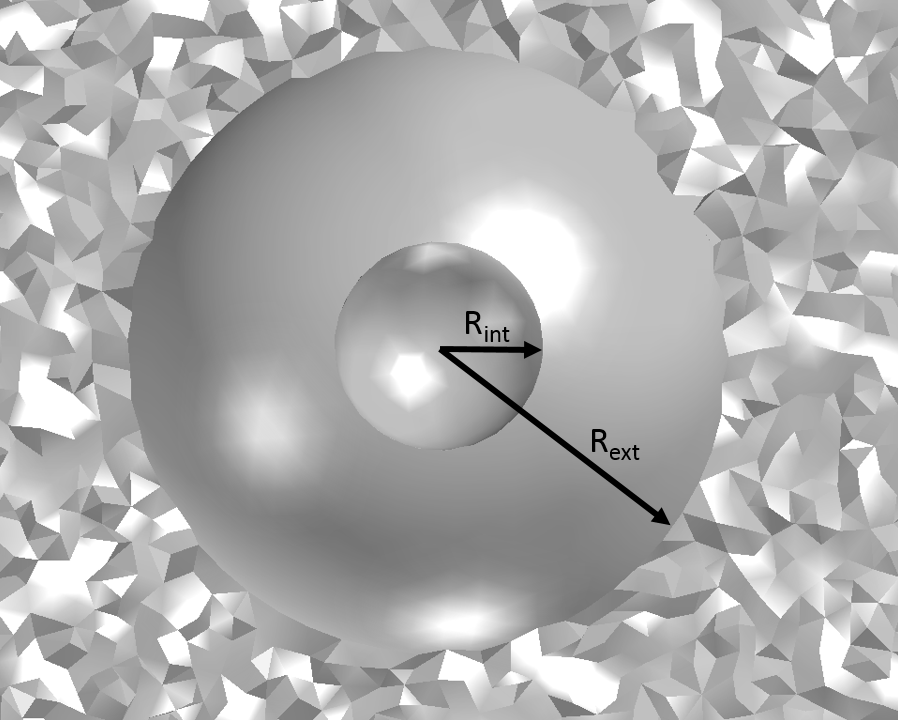
辐射发生在小球体的外侧和大球体的内侧之间。几何角系数为:
- F_{S_{\textrm{ext}}-S_{\textrm{ext}}}=1-\left(\frac{R_{\textrm{int}}}{R_{\textrm{ext}}}\right)^2
- F_{S_{\textrm{ext}}-S_{\textrm{int}}}=\left(\frac{R_{\textrm{int}}}{R_{\textrm{ext}}}\right)^2
- F_{S_{\textrm{int}}-S_{\textrm{int}}}=0
- F_{S_{\textrm{int}}-S_{\textrm{ext}}}=1
式中,Sint 和 Sext 分别代表内部和外部球体。
在 COMSOL Multiphysics 中验证
为了在 COMSOL Multiphysics 仿真软件中计算几何角系数,我们需要添加一个激活表面对表面辐射的热接口,然后绘制几何图形并创建网格。
我们不需要运行传热仿真,因为我们只对几何角系数感兴趣。访问 radopu 和 radopd 运算符就能获得初始值。
不过,在这之前,我们最好准备一些可以帮助我们进行后期处理的工具。
表面指示器
在几何角系数表达式中,我们使用了表面指示器 I_{\textrm{S1}} 和 I_{\textrm{S2}}。这些指示器在 COMSOL Multiphysics 中被定义为变量,并使用了几何实体选择,因此除了在相应的表面上是 1 之外,其他地方都是 0。我们把它们命名为 ext 和 int。
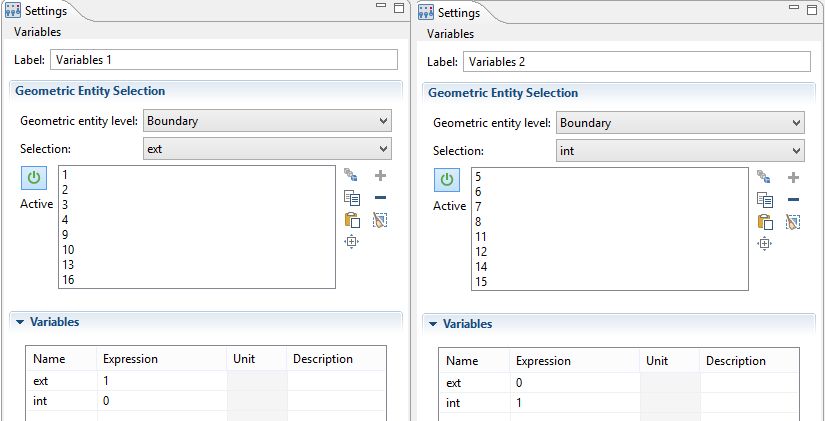
表面指示器的几何实体选择设置的屏幕截图。
在 S int 和 Sext 上积分
接下来,我们定义积分运算符 intop_ext 和 intop_int。这样计算表面积分会变得容易一些;例如,Sext 的表面可以被计算为 intop_ext(1)。
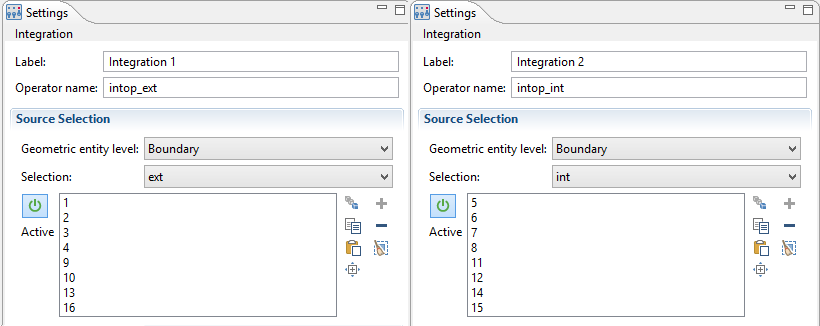
积分算子的设置屏幕截图。
验证边界的辐射面
我们已经看到,辐射可能发生在边界的上侧、下侧或两侧。设计辐射算子是为了能够区分来自每一侧的辐射。因此,我们需要检查这个模型各个边。
我们可以通过漫反射表面功能轻松做到这一点,辐射方向可以设置为 “负法线方向”(向下)或 “正法线方向”(向上)。使用这个选项会提示自动显示箭头,来表示离开表面的辐射方向。在我们的例子中,辐射发生在 Sext 的下侧和 Sint 的上侧。
计算几何角系数
有了这些软件提供的方法,使用类似于等式(1)的表达式来计算角系数是直接的。比如,
(3)
{ext}}}=\frac{\int_{S_{\textrm{ext}}}{\textrm
{radopd}(0,I_{S_{\textrm{ext}}})ds}}{\int_{S_{\textrm{ext}}}{1}}
在 COMSOL Multiphysics 语法中,用 intop_ext(comp1.ht.radopd(0,ext))/intop_ext(1) 进行计算。
请注意,使用 radopd 是因为辐射发生在 Sext 的下侧。同样,radopd 的第一个参数为 0。使用 intop_ext(comp1.ht.radopd(int,0))/intop_int(1) 计算
(4)
(I_{S_{\textrm
{int}}},0)ds}}{\int_{S_{\textrm{int}
}}{1}}
使用 radopd 算子是因为辐射发生在 Sext 的下侧。但是这一次, radopd 的第二个参数是 0,因为辐射发生在 Sint 的上侧。
将所有结果列在下表中:
| 解析值 | 计算值 | 误差 | |
|---|---|---|---|
| F_{S_{\textrm{int}}-S_{\textrm{int}}} | 0 | 0 | 0 |
| F_{S_{\textrm{int}}-S_{\textrm{ext}}} | 1 | 0.998 | 2e-3 |
| F_{S_{\textrm{int}}-S_{\textrm{ext}}} | 0.91 | 0.9102 | 2e-4 |
| F_{S_{\textrm{ext}}-S_{\textrm{int}}} | 0.09 | 0.09 | 1e-6 |
有了辐射算子,我们就可以获取几何角系数。
总结
COMSOL Multiphysics 5.0 中内置了专门的算子,因此我们可以计算漫反射表面之间的几何角系数。在表面对表面功能发布后,这些算子解决了用户提出的需求。它们还可以做更多的事情。它们足够灵活,可用于计算表面对表面辐射方程中的所有项,还可为其他量定制方程。



评论 (2)
博清 张
2024-08-15请问我现在需要将角系数作为变量设置成边界条件,这个应该如何操作?使用文章中的radopd算子被软件反馈为无法识别的函数
Haoze Wang
2024-08-29 COMSOL 员工您好,建议您在后处理中计算得到角系数的值,直接设置在对应的边界条件中或将数据导出后再通过插值函数等导入模型进行设置。