“案例下载”页面提供丰富的 COMSOL Multiphysics® 教学案例和 App 演示文件,涉及电气、结构、声学、流体、传热和化工等各个学科领域。欢迎下载这些教学案例或 App 演示文件及其随附的操作说明,将其作为您建模仿真工作的绝佳起点。
您可以使用左侧的【快速搜索】工具查找与您的专业领域相关的案例模型和仿真 App。请注意,此处提供的许多案例也可以通过 COMSOL Multiphysics® 软件内置的“案例库”进行访问,该选项位于软件的文件 菜单中。
中文 带有此标签的案例包含中文 PDF 文档。
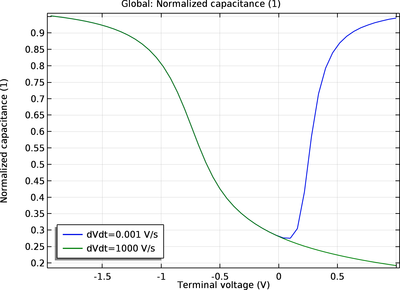
金属-氧化物-硅 (MOS) 结构是许多硅平面器件的基本构建块,其电容测量法可以帮助用户深入了解此类器件的工作原理。本教学案例构建了一个简单的 MOS 电容器 (MOSCAP) 一维模型,计算低频和高频 C-V 曲线。 扩展阅读
根据给定栅压的漏源电压,MOSFET 通常有三种工作模式。漏源电压较小时,电流与电压呈线性关系,这是欧姆区;随着漏源电压的升高,引出电流开始饱和,这是饱和区;随着漏源电压进一步升高,进入击穿范围 ... 扩展阅读
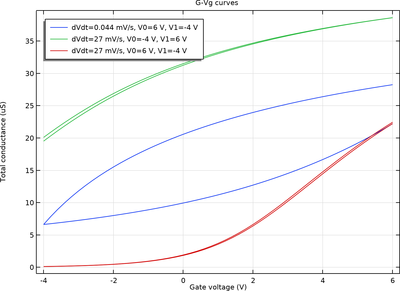
本教程分析 InAs 纳米线 FET 的电导-栅极-电压 (G-Vg) 曲线的滞回现象,使用密度梯度理论将量子限域效应添加到传统的漂移-扩散公式中,不会大幅增加计算成本。这种滞后现象是由连续能量分布 ... 扩展阅读
这个教学案例求解由简谐势阱束缚的旋转玻色-爱因斯坦凝聚体中涡格形成的 Gross–Pitaevskii 方程,这本质上是一个非线性单粒子薛定谔方程,粒子间的相互作用通过与局部粒子密度成比例的势能贡献表示 ... 扩展阅读
本例中的纳米线 MOSFET 三维模型使用密度梯度理论在传统的漂移-扩散公式中引入量子限域效应,而不需要过高的计算成本。其中使用几何域对氧化层进行显式模拟,并通过专用的边界条件来分析氧化硅界面的量子限域 ... 扩展阅读
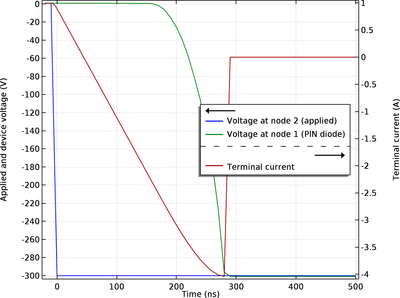
本教学案例大致基于 B. J. Baliga 编写的 "Fundamentals of Power Semiconductor Devices" 一书(2008 年版,第 256 页),模拟了带电感负载的简单 PIN ... 扩展阅读
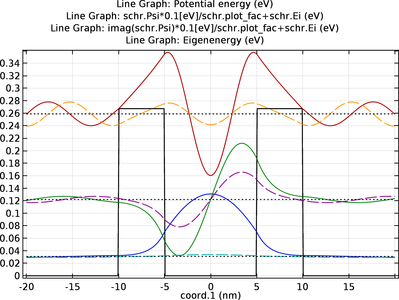
双势垒结构因其在共振隧穿二极管等半导体器件中的应用而受到关注。 此验证示例演示如何在薛定谔方程 接口中建立简单的一维砷化镓/铝砷化镓双势垒结构,分析准束缚态及其时间演化、共振隧穿现象以及透射随能量变化的情况 ... 扩展阅读
本模型展示了如何计算 MOSFET 的交流特性,根据漏极电流计算了器件的输出电导和跨导。 扩展阅读
表面声学声子和表面粗糙度对载流子迁移率具有重要影响,尤其是在 MOSFET 栅极下的薄反转层中。Lombardi 表面迁移率模型使用 Matthiessen 定则将这些影响产生的表面散射添加到现有的迁移率模型。 ... 扩展阅读