
网格自适应的目标是通过修改网格实现更高效地求解。通常,我们希望使用尽可能少的网格单元获得精确的解,在不太重要的区域使用较粗的网格,在感兴趣的区域使用较精细的网格。有时,我们甚至可能会考虑各向异性单元。从 5.4 版本开始, COMSOL Multiphysics® 软件包含了一些增强方法以调整网格。这篇博客,让我们来看看如何使用这些方法。
确定所需网格单元的大小
要对网格进行自适应操作,必须知道所需的网格单元大小。然而,找到合适的网格大小并不容易,事实上这需要进行大量的研究。对于稳态和特征值问题,我们可以使用COMSOL Multiphysics 中的 自适应和误差估计 功能基于内置的误差估计自动调整网格。
COMSOL 软件中的网格自适应方法并不局限于使用内置的误差估计,它还具有更高地灵活性。可以先在粗网格上求解一个较简单的问题,然后基于此解通过求解一个表达式来控制较难问题的单元大小。另外,还可以使用导入的插值函数或任何自定义表达式来控制单元大小。
本文不讨论这方面内容,而是假设已经隐式或显式地知道所需的单元大小是 x,y 和 z(三维空间)的函数。也就是说,网格单元的边长由该边中点坐标的函数表达式确定。当然,一般情况下不可能完全满足此要求,即使是一个三角形单元也需要满足三角形不等式。但是,请记住:大小表达式代表空间中每个点所需的单元边长。
根据大小表达式调整网格的 2 种方法
COMSOL Multiphysics 的 网格节点下有 2 种不同的方法可以构建适应大小表达式的网格。
第一种方法,我们可以在网格划分序列中使用大小表达式 属性来改变生成网格的大小。如果使用研究中的网格自适应功能,则相当于选择了 重新生成网格 选项,其中的自由网格生成器(自由三角形网格,自由四边形网格和自由四面体网格)会考虑网格大小。另一方面,例如 映射 、扫掠 和某种程度上的 边界层)会忽略大小表达式属性(根据定义,结构化网格不能遵循大小可变的字段)。简单来说,就是如果我们构建的是结构化网格,可能无法使用此方法。
另一种方法是使用 自适应 操作。此操作通过单元细化和粗化来修改现有网格。我们可以在具有任何单元类型的网格上以及在导入的网格上使用 自适应 操作。这是一种更强大的方法,并且可能更好地遵循指定的大小表达式。但是,结果通常不如从头开始生成的网格平滑。
下面,我们将详细讨论这 2 种方法,并看看二者产生的结果有何不同。
使用大小表达式属性
如前所述,使用大小表达式属性方法通常能获得高质量的网格。但是,如果这种方法产生的单元质量较差(在大小过渡较快时会出现这种情况),则可能无法达到所需的单元大小。有关网格质量的讨论,请阅读博客:如何检查 COMSOL Multiphysics® 中的网格质量。由于每次调整都是从头开始构建网格,因此对于复杂的几何结构而言,此过程可能非常耗时。
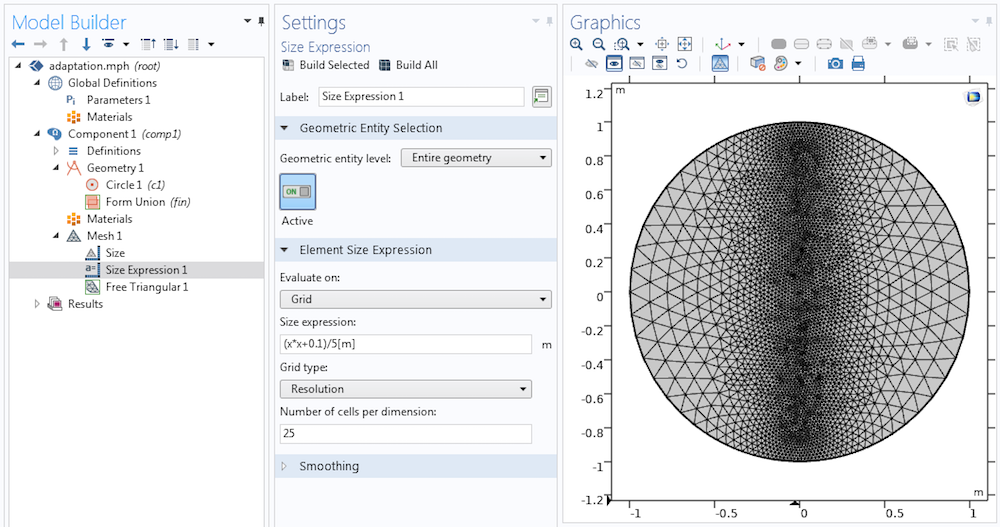
使用 大小表达式 属性对一个圆形几何的三角形网格应用大小表达式,得到高质量的网格单元和大小过渡平滑的网格。
如果已知大小表达式(例如,一个全局插值函数),在背景栅格上进行计算通常很方便(上图中的基于栅格计算)。需要确保栅格分辨率足够高,才能捕获大小表达式描述的所有特征。
当大小表达式取决于已知的空间变化量(例如材料),可以使用 初始表达式 计算选项。这样,就可以使用模型中的任何表达式。软件将在求解前计算表达式(与可用于研究步骤的 获取以下步骤的初始值 命令对比)。我们还可以指定某个研究步,因为一些表达式的值取决于研究。
最后,还可以基于现有解计算。内置的 误差 估计使用的是 误差指示器 表达式类型 ,但也可以使用任意的大小表达式,这取决于现有的解决方案。例如,有时可能想在应力较大的地方细化网格。
使用自适应操作
另一种方法是基于现有的网格进行修改来匹配所需的单元大小。这就是 自适应 操作的作用。它适用于所有单元类型,也可作用于导入的网格。它的许多选项和输入字段与 大小表达式 属性相同。
该操作有三种适应方法:最长边细化,常规细化 和 通用修改。前两种细化方法是基于单元边的二等分法操作。由于这些单元边太长,所有现有网格的顶点被保留,因此这些方法无法被粗化。 自 5.4 版本开始,COMSOL Multiphysics 软件内置了 通用修改 方法。顾名思义,就是以非常通用的方式修改网格:
- 单元可以被细化
- 如果网格太细,可以通过删除顶点来粗化网格
- 可以通过单元修改,移动网格顶点来提高网格质量
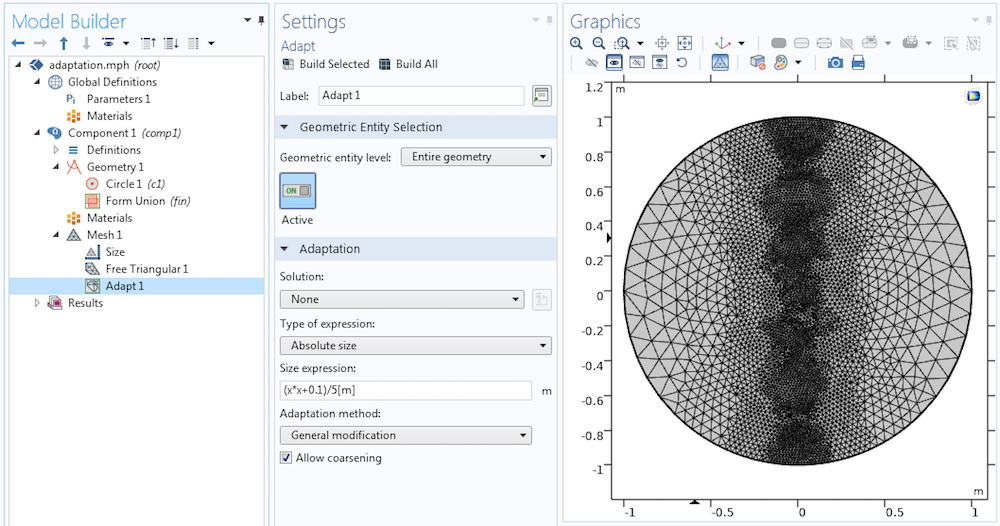
使用 自适应操作 的 通用修改 方法,对 大小表达式 属性应用同一表达式。对于大多数应用而言,虽然网格单元质量足够高,但是大小过渡不如从头开始生成的网格平滑。
如果将自适应方法更改为 最长边细化,结果如下图所示。过长的边将被一分为二,直到网格被充分细化。这种网格操作非常快,但是即使输入网格的质量很高,该方法常常会产生低质量网格单元。
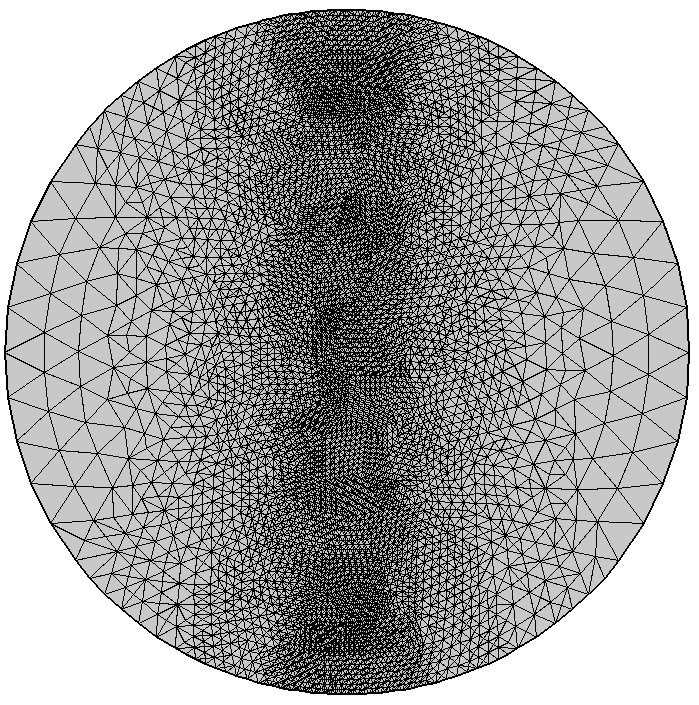
与上述模型相同,但是将自适应方法设置为 最长边细化。在这幅图中,可以看到原始三角形形状产生的图案。
支持所有单元类型
自适应 操作适用于所有单元类型的网格,也可以用于结构化网格域(虽然网格自适应后通常不再是结构化)。但是,当在四边形单元(二维)、六面体单元(三维)、棱柱单元和金字塔单元等复杂单元中使用此方法时,必须要小心,因为得到的结果可能很差。下面,我们来看看在这种情况下单元大小是如何过渡的。在二维模型中,三角形网格单元被插入四边形网格中。
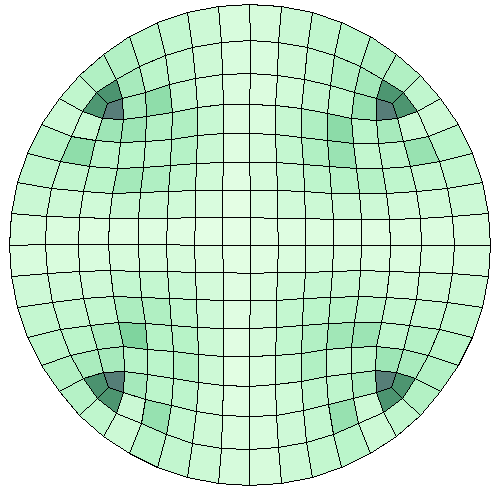
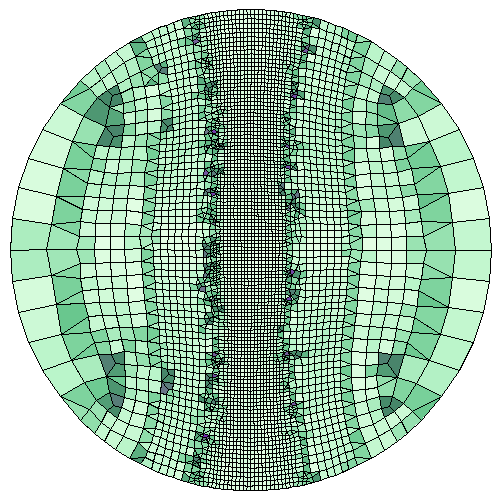
左图:圆形几何中默认的 自由四边形 网格。以最大角度质量对单元进行着色。右图:适应后的网格与上文中的大小表达式的结果相同。请注意在大小过渡区域中三角形单元的使用。
在三维结构中,四面体和金字塔常用于大小过渡区域,在合适的情况下也可以插入其他单元类型。下图显示了一个划分粗六面体网格的圆柱,该圆柱使用 0.02 + z*z 表达式进行适应。
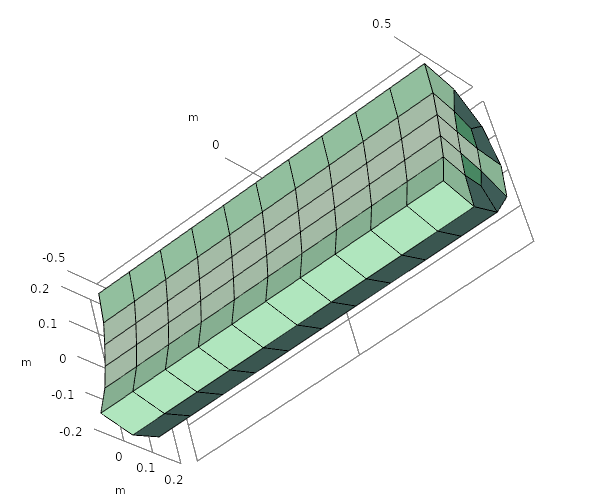
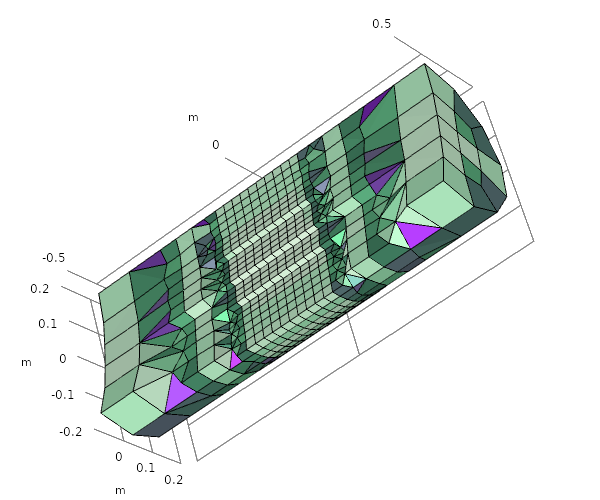
自适应前后的圆柱体网格。
对边界层网格进行网格自适应操作
在以上所有示例中,指定的大小函数表示各向同性单元的大小。即,理想形状单元所有边的长度都(大约)相同。如果需要适应的网格是各向异性的(例如,单元沿边界延伸的边界层网格),自适应就会朝着各向同性方向修改网格。边界层单元甚至可能会被完全删除!这并不是我们想要的结果。一种解决方法是禁止粗化操作,这样边界层就会被保留。
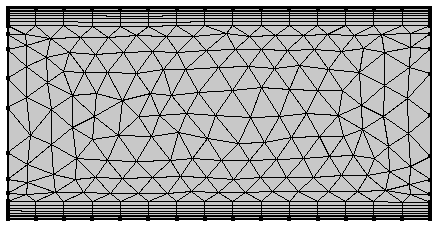


左图:以原点为中心的矩形,含边界层网格。中图:适应方法为通用修改,大小表达式 为 0.04 + x*x。由于粗化操作,边界层被删除了。右图:禁用粗化操作的自适应结果,边界层被保留。
构建各向异性网格
自适应 操作同样适用于各向异性适应。各向异性网格单元是指理想单元在某个方向上被拉伸的单元。这种网格在 CFD 计算中很常见,一个典型的例子就是边界层网格。要实现各向异性适应,可以先选择 各向异性度量 作为表达式类型。然后,需要指定一个 2×2(二维)或 3×3(三维)对称矩阵。此操作意味着:表示单元边的向量在该点被矩阵转换,并测量转换后向量的长度。如果长度小于 1.0,则认为太短;如果长度大于 1.0,则认为太长。此度量标准用于控制适应过程。下图显示了如何使用此方法。
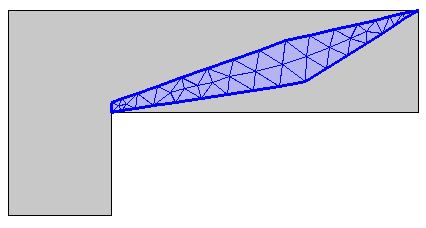
使用三角形单元划分网格控制域。
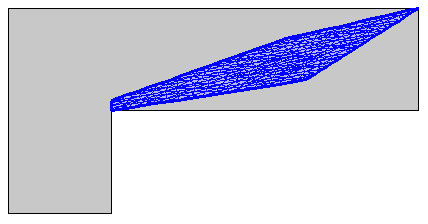
使用各向异性适应方法划分网格。这个示例中,度量标准由常数矩阵 \begin{pmatrix}10 & -10 \\-10 & 60\end{pmatrix} 指定。
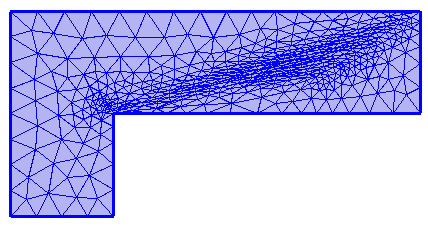
使用自由三角形网格对控制域周围的域进行网格划分。

将网格控制域合并到更大的域中。
结语
这篇博客展示了如何使用 COMSOL Multiphysics 中的网格自适应方法来创建适合特定目标的网格。一种方法是使用 网格 节点的 大小表达式 属性,此操作将控制生成的三角形和四面体网格的大小,通常可以得到平滑且质量较高的网格。另一个方法是使用 自适应 操作,该操作会修改现有的网格。网格自适应是一种强大的方法,可以修改任何类型的网格,也能生成各向异性网格单元。
下一步
了解有关 COMSOL Multiphysics 如何满足您的建模需求的更多信息,请单击下面的按钮,联系我们试用软件:
更多资源
- 在 COMSOL 博客上了解有关创建网格的更多信息:
- 查看相关教程模型:






评论 (0)