如果使用 COMSOL Multiphysics® 软件及其附加的 AC/DC 模块与优化模块进行电磁线圈设计,您将能够快速地提出优化的迭代设计。今天,我们将研究如何通过改变线圈的驱动电流来设计线圈系统,以实现所需的磁场分布,并介绍三种不同的优化目标和约束条件。如果您对线圈模拟或优化感兴趣,这篇博客将满足您的好奇心!
磁场模型与优化问题
我们要探讨的问题是优化一个 10 匝轴对称线圈结构,如下图所示。xy 平面两侧各有 5 匝线圈,其中每一匝线圈对称并分别通入驱动电流。
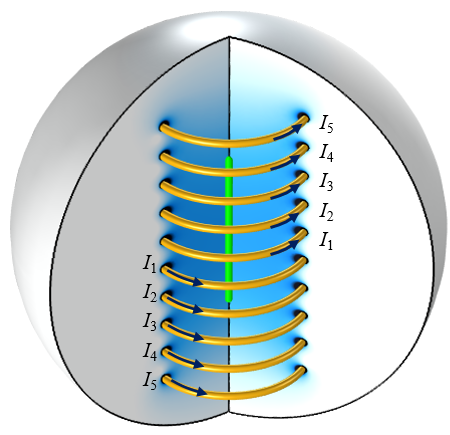
由 5 对独立的驱动线圈组成的 10 匝线圈。优化目标是改变中心线(用绿色突出显示)的磁场。
此示例线圈既具有旋转对称性,又关于 z=0 平面对称,因此可以将计算模型简化为二维轴对称模型,如下图所示。使用一个 无限元域 将模拟域截断。使用理想磁导体边界条件模拟关于 z = 0 平面的对称性。因此,模型被简化为一个 1/4 圆域,其中 5 个独立线圈使用 线圈域 特征模拟。
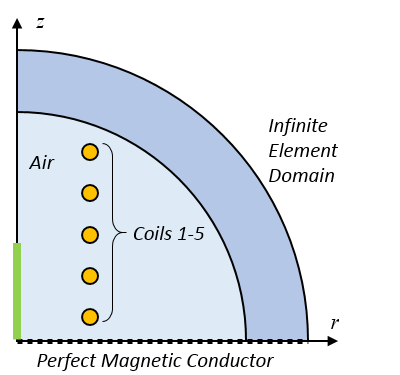
计算模型的示意图。
如果所有线圈均通入 10 A 的电流来驱动,可以绘制出中心线上磁通密度的 z 分量,如下图所示。我们的目标就是通过优化改变一部分中心线上的磁场分布。
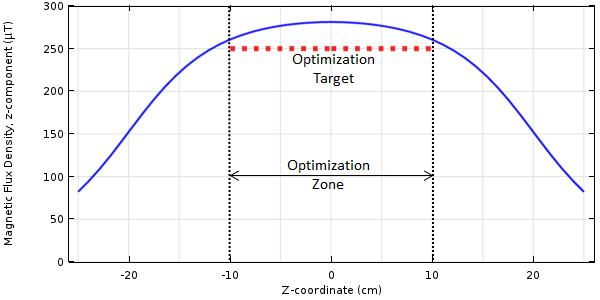
线圈中心线上的磁场分布。我们的目标是调整优化区域内的磁场。
从上图可以看出,由于每个线圈通入的电流都为 10 A,一部分中心线上存在磁场。我们希望通过调整线圈中的电流来改变磁场分布。控制变量为 5 个独立的线圈电流:I_1,I_2,\dotso,I_5。这些控制变量的边界条件为:-I_{max}\le I_{1,\dotso,5}\le I_{max},也就是说,电流不能过大,否则线圈会过热。
接下来,我们来研究三种不同的优化问题:
- 使中心线处的磁场尽可能接近期望的目标值
- 在几个点上对场量的最小值进行约束的情况下,尽可能降低驱动线圈所需的功率
- 在一个点上对场量的最小值进行约束的情况下,尽可能降低中心线上的磁场梯度
对特定场量进行优化
使用数学语言对这些优化问题进行描述,第一个优化问题可以表述为:
& \underset{I_1, \ldots ,I_5}{\text{minimize:}}
& & \frac{1}{L_0} \int_0^{L_0} \left( \frac{B_z}{B_0} -1 \right) ^2 d l \\
& \text{subject to:}
& & -I_{max} \leq I_1, \ldots ,I_5 \leq I_{max}\\
\end{aligned}
这个问题的目标是使计算得到的 Bz 场与目标值 B0 = 250 μT 之间的差异最小,该目标值是通过沿着线圈中轴线 Bz,从 z = 0 到 z = L0 进行积分得到的。注意,该目标已经相对于 L0 和 B0 进行了归一化处理。这样做是为了使目标函数的量级接近 1。对于任何一个优化问题,都应该对目标函数进行缩放。
现在,我们来看看如何在 COMSOL Multiphysics 中实现这个优化问题。首先在模型中添加一个 优化接口,该接口包含两个特征。第一个特征是 全局控制变量,如下面的屏幕截图所示。我们可以看到设置了 5 个控制变量:I1,...,I5。这些变量用于指定 磁场 接口中 5 个 线圈特征的电流。
通过 2 个 全局参数I_init 和 I_max ,指定这些变量的 初始值、上限 和 下限 。同时不要忘记设置 比例因子,以使控制变量的量级也接近 1。对于所有三个示例,使用相同的控制变量设置。
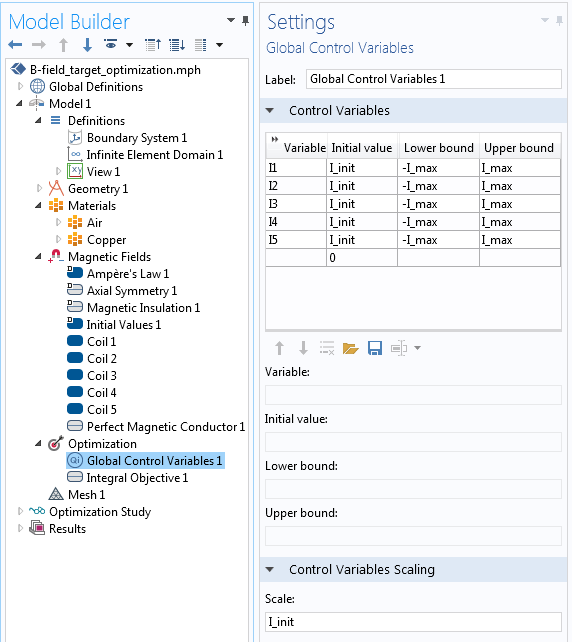
用于指定线圈电流的全局控制变量设置。
接下来,通过 积分目标 特征在边界上定义目标函数,如下图所示。请注意,乘以 2πr 选项未勾选。
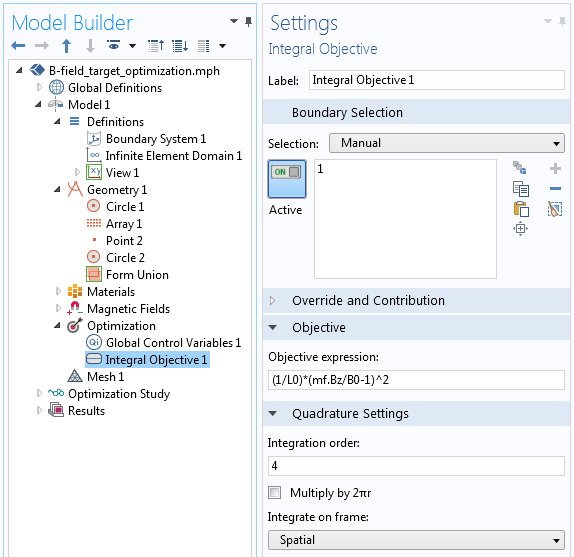
通过定义目标函数获得边界上的目标场。
如下图所示,我们在研究中添加了一个 优化 步骤。由于可以计算目标函数关于控制变量的解析梯度,我们可以使用 SNOPT 求解器。该求解器利用计算的解析梯度,在几秒钟内求解优化问题。其他所有求解器设置都可以保留为默认设置。
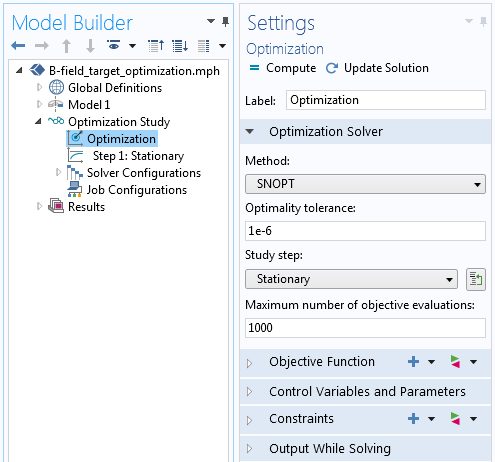
优化研究步骤。
求解完成后,我们可以绘制场和结果。下图显示了计算的 Bz 场与目标值非常接近。
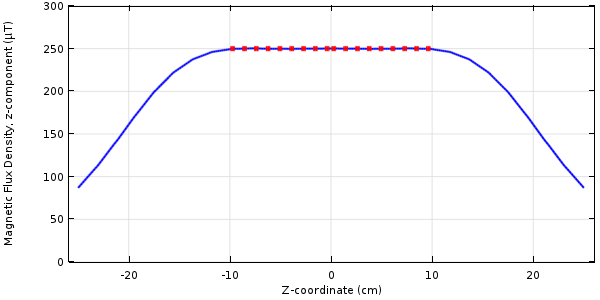
中心线上目标磁通量值的优化结果。
通过控制场量并尽可能降低功率
第二个优化问题是尽可能降低驱动线圈所需的总功率,并对中心线上若干点的场最小值进行约束。这个问题使用数学表达式可描述为:
& \underset{I_1, \ldots ,I_5}{\text{minimize:}}
& & \frac{1}{P_o}\sum_{k=1}^{5} P_{coil}^k \\
& \text{subject to:}
& & -I_{max} \leq I_1, \ldots ,I_5 \leq I_{max}\\
& & & 1 \le B_z^i/B_{0}, i=1, \ldots, M
\end{aligned}
式中,Po 是所有线圈消耗的初始总功率,P_{coil}^k 是第 k 个线圈消耗的功率。
进一步将中心线上 M 个点处的磁场限制在 B0 值以上。
使用与之前问题相同的全局控制变量特征实现优化,并通过 全局目标 特征尽可能降低线圈总功率,如下图所示。可以直接使用每个线圈特征中的内置变量(mf.PCoil_1,...,mf.PCoil5)表征消耗的功率。将相对于初始总功率的目标值进行归一化处理,以使其接近 1 。
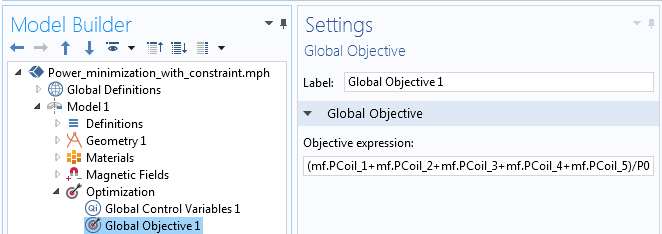
将目标总功率值降至最低的设置。
必须使用模型中的一组离散点实现对场的最小值约束。本例中,我们在优化区域引入了均匀分布的 5 个点。如下图所示,每一个约束必须使用单独的 点总和不等式约束 特征添加。再次进行归一化处理,使此约束的大小为 1。请注意,因为这些点位于中心线上,所以 乘以 2πr 选项未勾选。
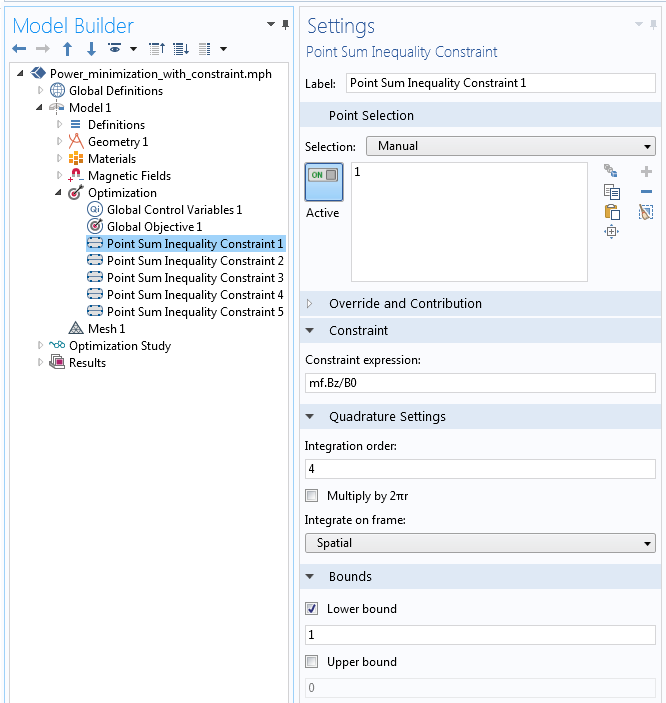
在某一点上控制场量为最小值。
我们可以使用与之前问题相同的方法来求解这个问题,结果如下图所示。值得注意的是,求解的最小的功率并未在目标区域产生均匀分布的磁场。
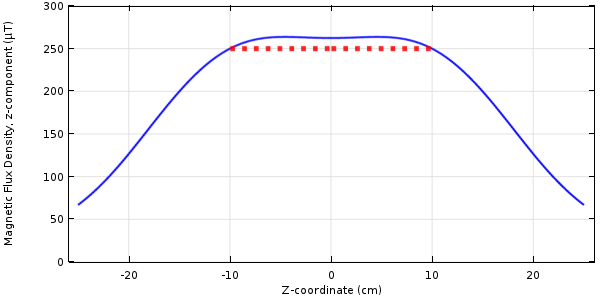
通过控制场量为最小值尽可能降低消耗的功率的结果。
通过控制场量并尽可能降低磁场梯度
最后,我们考虑尽可能降低优化区域的磁场梯度,在中心点对场进行约束。使用数学表达式可以将此问题描述为:
& \underset{I_1, \ldots ,I_5}{\text{minimize:}}
& & \frac{1}{L_0 B_{0}} \int_0^{L_0} \left( \frac{\partial B_z}{\partial z } \right) ^2 d l \\
& \text{subject to:}
& & -I_{max} \leq I_1, \ldots ,I_5 \leq I_{max}\\
& & & B_z(r=0,z=0) = B_0 \end{aligned}
这里的约束规定线圈中心点处的场。尽管 优化 接口有明确的等式约束,但可以通过设置上限和下限相等的不等式约束获得相同的结果。再次进行归一化处理,以使约束实际上为 1 \le B_z/B_0 \le 1,如下图所示。
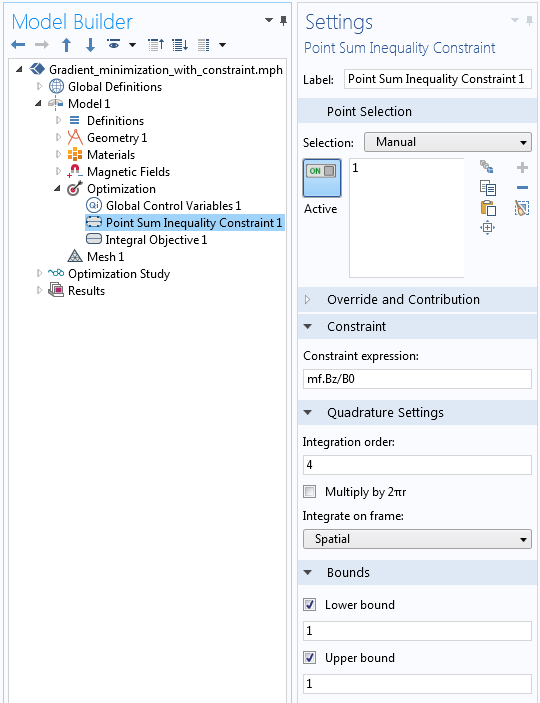
实现等式约束的设置。
尽可能降低目标区域内场的梯度的目标是通过积分目标特征实现的(如下图所示)。相对于 z 轴方向的 Bz 场梯度是使用导数算子 d(mf.Bz,z) 计算的。
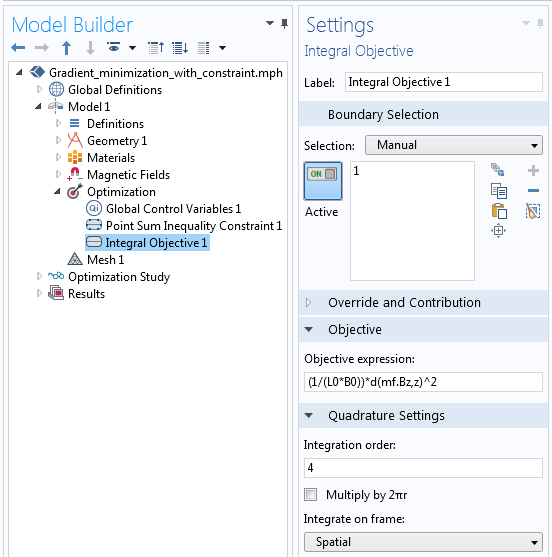
尽可能降低场梯度的积分目标设置。
我们可以使用与之前相同的求解器设置。这个示例的优化结果如下图所示。可以看出,优化区域内的场非常均匀,并且与中心点的目标值一致。
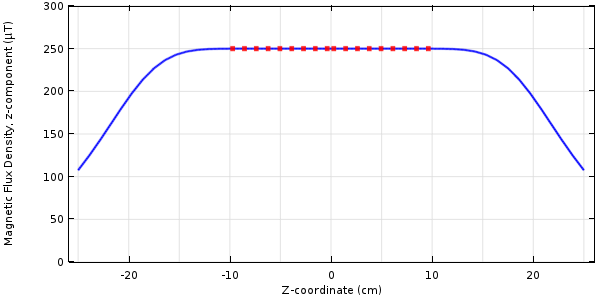
使用约束条件尽可能降低某一点处场梯度的优化结果。
虽然这个示例中优化后的场看起来与第一个示例几乎完全相同,但线圈电流的解却截然不同,这就引出了一个有趣的问题。存在多种线圈电流组合,能在尽可能降低场差异或梯度方面得到几乎相同的解。也就是说,目标函数有多个局部最小值点。
SNOPT 优化求解器采用了基于梯度的方法,对不同的线圈电流在不同初始条件下求解局部最小值。虽然基于梯度的求解器将收敛于局部最小值,但不能保证这就是全局最小值。一般来说(除非对在设计空间内进行彻底的搜索),永远不可能保证优化的解就是全局最小值。
此外,如果要增加这个问题中的线圈数量,可能会遇到线圈电流的多种组合几乎同样最优的情况。也就是说,设计空间(即线圈电流的组合)内不存在单个最优点,而是存在值几乎相等的“最优线”或“最优表面”。优化求解器不会直接反馈这一点,但在这种情况下往往会收敛得更慢。
结束语
这篇文章,我们介绍了 3 种不同的方法来优化线圈不同匝中的电流。在这 3 种方法中,我们引入了不同类型的目标函数和约束,这些函数和约束也适用于其他各种情况。根据线圈设计问题的整体目标和要求,您可以使用其中任何一个,甚至完全不同的目标函数和约束集。这些示例表明同时使用 COMSOL 优化模块与 AC/DC 模块的强大功能和灵活性。
当然,对于这些问题,还可以做更多研究。在即将发布下一篇的博客中,我们将重点关注调整线圈匝的位置,敬请关注!
编者注:此系列博客的后续内容已经发布。点击此处阅读:“如何优化电磁线圈的间距”。
扩展资源
- 浏览 COMSOL 博客,了解有关电磁线圈仿真的更多信息:






评论 (2)
Andy Du
2022-11-15帮忙分享一下计算文件,谢谢
hao huang
2022-11-17 COMSOL 员工相关案例请参考:https://cn.comsol.com/model/optimizing-coils-48041