
COMSOL Multiphysics® 软件常用于求解涉及偏微分方程 (PDE) 场解的问题,但也可以求解常微分方程 (ODE)。例如,我们可以通过求解牛顿第二定律来解决卫星绕行星运动的问题。求解这个方程非常简单,我们可以结合使用 COMSOL 软件的求解功能与结果呈现功能,制作一些非常漂亮的可视化效果图。接下来,让我们了解更多内容!
计算卫星轨道
在对绕地球运行的卫星进行建模时,我们可以先写出卫星受到的引力表达式:
其中,\phi 是一个势函数。
我们将使用以地球为中心的笛卡尔坐标系。考虑到地球略呈非球形这一事实,使用以下表达式来表示势能:
其中,\mu_{\oplus} 是地球的标准引力参数,r 是地球中心到卫星的距离,J_2 是地球位势模型的球谐展开式的第二项,P_2 是第二个勒让德多项式。
势能中的第二项解释了地球赤道隆起并导致了卫星进动。
我们可以使用 COMSOL Multiphysics 中内置的一个数学函数—— legendre() 函数写出势能表达式。还可以使用内置算子 sum() 在势能函数中包含高阶项,但在本文的这个例子中它们非常小,所以忽略了这些项。
如果假设卫星上只有引力,那么卫星位置的控制常微分方程可以写为:
求解这个方程需要位置的初始条件 \mathbf{ {x}}_0 和速度 \mathbf{\dot {x}}_0。卫星的位置通常以开普勒轨道单元的形式给出。对于一般的椭圆轨道,由偏心率 \epsilon,半长轴 a,交角 \epsilon,升交点经度 \Omega 以及近心点角 \omega 定义一个椭圆。真正的近点距离 \nu 定义了开始时沿该椭圆的位置。升交点的经度、倾角和近点角对应于 Z-X-Z 真欧拉角,我们可以使用 COMSOL Multiphysics 中的 旋转坐标系 特征完成定义。当定义好坐标系后,如下图所示,它提供了一组九个矩阵分量,可以通过这个坐标系转换。
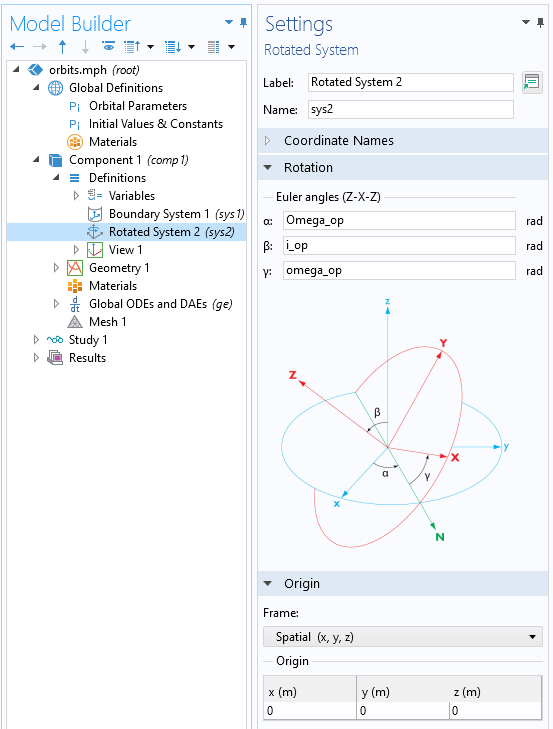
旋转坐标系特征的屏幕截图。
例如,如果我们将初始真近点角 \nu_0, 赋于升交点(当卫星向上穿过赤道时),就可以通过更多的数学计算来计算卫星在轨道平面中的初始位置和速度。然后,我们可以使用变换矩阵的分量来获得全局坐标系中相对于行星中心的初始位置。由此,我们有了完整的模型定义,并准备好设置常微分方程并对其进行求解。
我们可以使用 全局常微分方程和微分代数方程 接口并输入全局坐标系中位置的方程,如下面的屏幕截图所示。简单地把 t 到加到要求解的变量就会得到时间导数,加两次就会得到二阶时间导数,因此表达式 X_stt 等价于加速度矢量的 x 分量。另一方面,当处理诸如引力势之类的表达式时,是通过 d() 算子完成微分的,所以 d(Potential,X_s) 是引力的 x 分量。
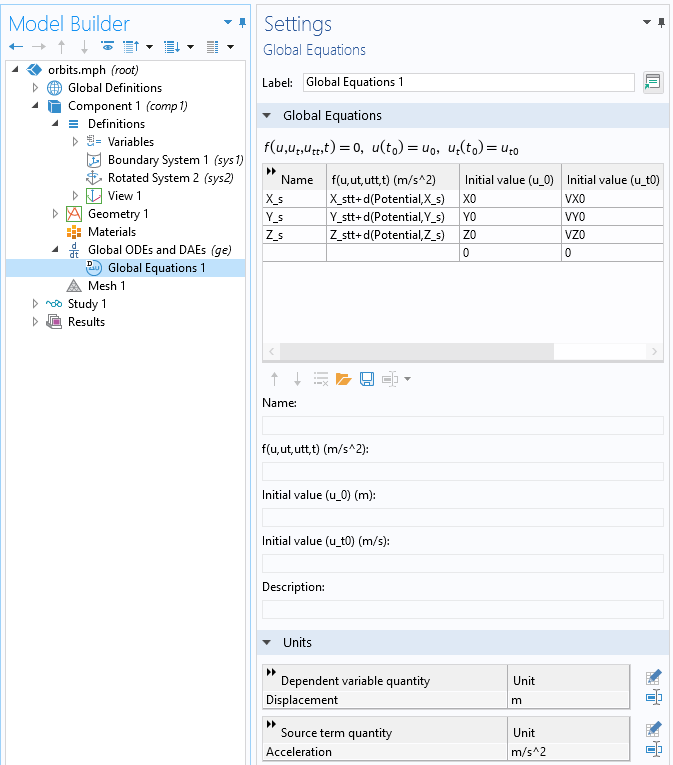
求解关于行星中心的卫星位置的 常微分方程。注意变量和方程的单位是如何设置的。
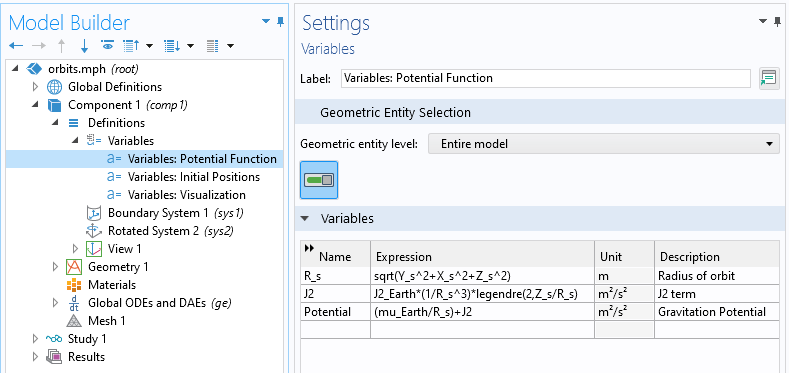
求解该位置的常微分方程需要定义半径和引力势的表达式。
这组方程和常微分方程可以用任何类型的瞬态求解器求解,但无论哪种类型,我们都需要研究相对容差。根据其他建模需求,可能首选默认的 BDF 求解器,因为它还允许:在瞬态求解期间隐式触发方程中的变化。
可视化轨道
当求解决了方程,我们就可以绘制卫星的位置和高度随时间的变化,我们可能还想绘制轨道上的航天器可视化图像。为此,接下来我们看看如何使用一些结果可视化功能。假设我们有一个代表我们的航天器的 CAD 模型,如下图所示。图中还显示了一组矢量,用于定义面向速度和面向天底的方向。正如已通过 旋转坐标系 特征所描述的,这两个单位矢量的叉积平行于轨道平面的法线。
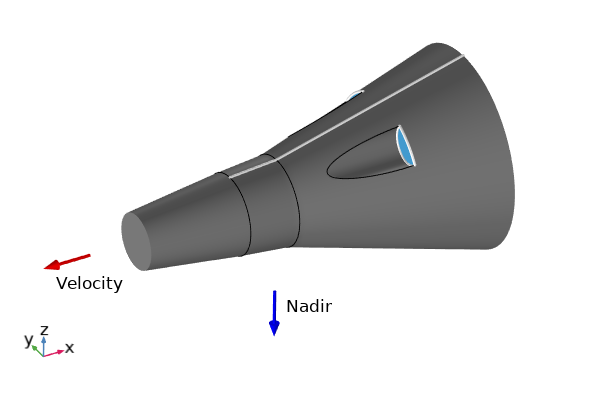
航天器的简单 CAD 模型,显示了其在轨道上是如何定向CAD 坐标系的矢量。
在绘制航天器之前,我们要做的第一件事是创建地球的可视化图像。为此,我们可以使用参数化表面 数据集,根据纬度和经度写出球体的表达式。
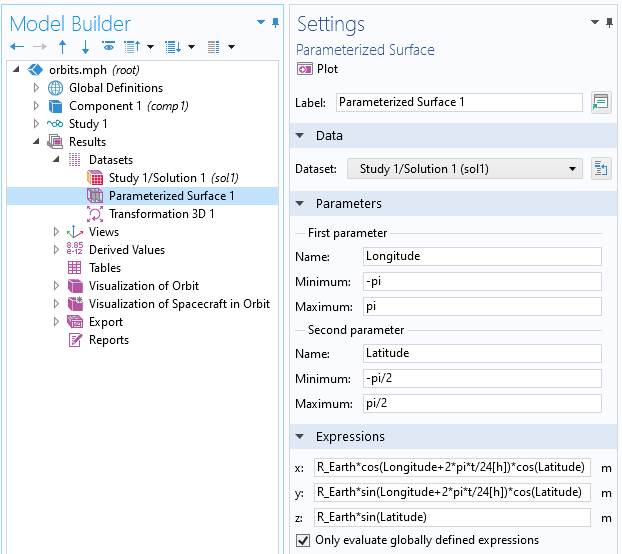
参数化表面 数据集,可用于生成简单的基于形状的表达式,例如球体。
我们现在可以使用 图像 绘图功能来显示映射到数据集的图像。由于参数化表面是根据纬度和经度设置的,因此可以将使用等量矩形投影的图像映射到其上,如下图所示。
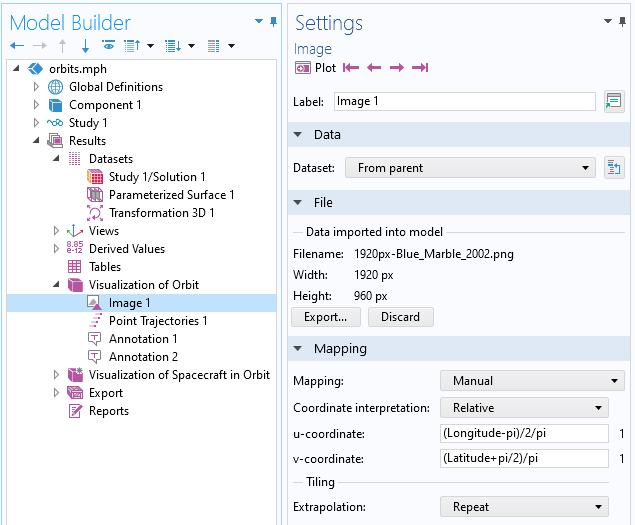
在 参数化表面 数据集上绘制的图像数据。
接下来,我们可能还想绘制轨道路径。这可以通过 点轨迹 绘图类型来完成,它允许我们输入轨迹数据和航天器随时间的位置,并沿着其路径绘制一条线。此外,标注 绘图类型允许我们评估和绘制沿路径变化的表达式。
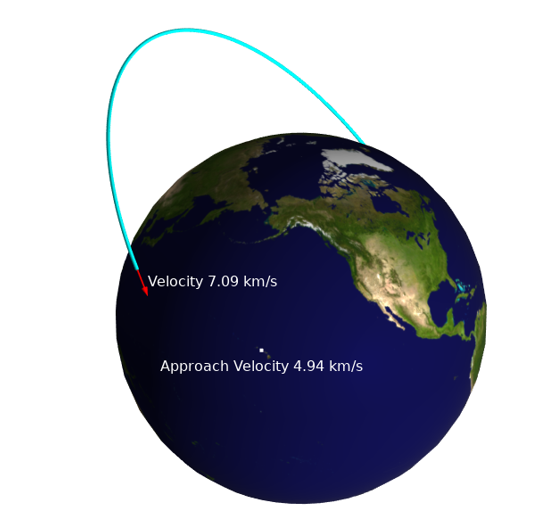
使用点轨迹和标注绘图工具来可视化卫星轨道和速度信息,以及相对于地面站的速度。
最后,我们来绘制一个航天器绕地球运动的比例可视化图。这可以通过变换三维 数据集来完成,该数据集允许根据一组基本向量和平移向量适当地缩放和重新定向航天器的一般转换类型。简单来说,就是我们只使用定义速度和最低点方向的向量以及垂直于轨道平面的向量来重新定位航天器围绕地球的方向,如下所示。
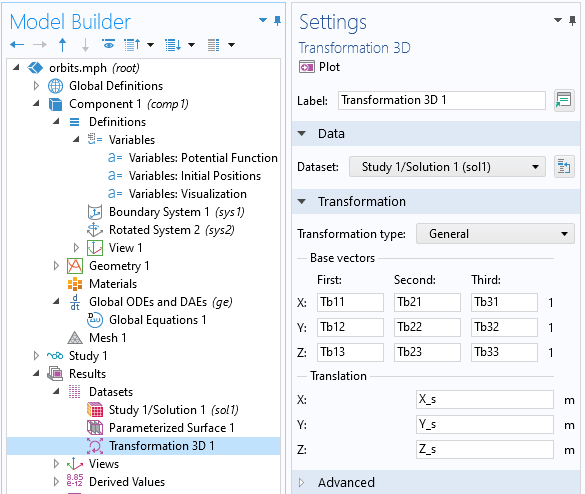
变换三维 数据集可用于重新定向数据集。
宇宙飞船在地球轨道上的动画。
结束语
本文我们演示了如何求解计算卫星绕行星运动的常微分方程。在引力势函数中包含更多项以查看它们的贡献非常简单,并且可以将额外的力添加到常微分方程来解释大气阻力和其他导致轨道衰减的因素。
或者,为了简化问题,我们可以用随时间变化的位置显式方程的替换这个常微分方程。不过,无论我们如何计算该轨迹,都可以使用结果功能来创建各种有趣且有用的可视化效果。
动手尝试
单击下面的按钮,进入 COMSOL “案例库”,尝试自己建立轨道上的航天器模型:
NASA Goddard Space Flight Center Image by Reto Stöckli (land surface, shallow water, clouds). Enhancements by Robert Simmon (ocean color, compositing, 3D globes, animation). Data and technical support: MODIS Land Group; MODIS Science Data Support Team; MODIS Atmosphere Group; MODIS Ocean Group Additional data: USGS EROS Data Center (topography); USGS Terrestrial Remote Sensing Flagstaff Field Center (Antarctica); Defense Meteorological Satellite Program (city lights).






评论 (0)