
众所周知,COMSOL 的 RF 模块可用于计算无损传输线结构的阻抗,如具有均匀截面的同轴电缆。但你知道吗,COMSOL 也可以计算非均匀截面波导的有效阻抗?让我们来了解一下!
计算直线同轴电缆的阻抗
首先,让我们来看一种最常见的传输线结构——同轴电缆。该电缆的内部和外部导体被电介质隔开,波将以 TEM 模式沿着电缆的长度方向传播,这意味着电场和磁场是横向传输的。
如果可以假设导体和电介质是无损耗的(对大多数情况来说,这是一个很好的近似),我们就可以计算出阻抗,例如 COMSOL 案例库中关于寻找同轴电缆阻抗的基准示例所示。
在这个示例中,我们绘制了同轴电缆的二维横截面,并指定电介质特性,以及低于任何 TE 或 TM 模式截止频率的工作频率。然后,COMSOL 软件将求解面外传播常数以及场的特征值,用于计算电缆的阻抗。这种方法计算效率很高,但只适用于均匀截面的 TEM 模式波导。
计算波纹同轴电缆的阻抗
现在,让我们考虑一个外导体为波纹的同轴波导。当需要机械灵活性时,就会用到这种类型的波导。
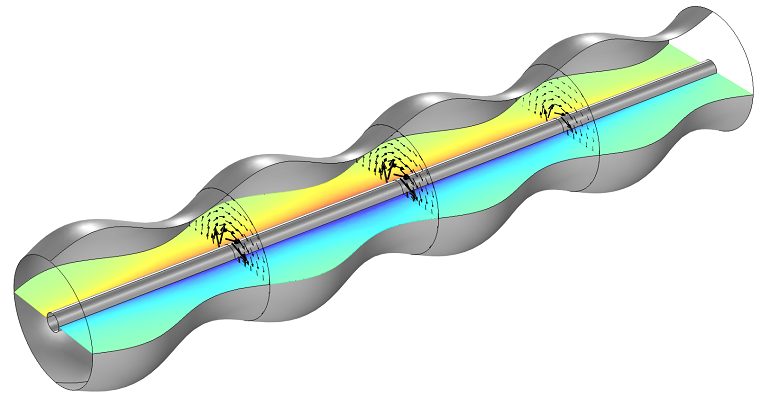
一根波纹状同轴电缆。切面图为电场,箭头图为磁场。
这种波导不会在纯 TEM 模式下工作,也就是说,在传输方向上有一些电场和磁场分量。但是,我们将假设这些分量很小,因此可以将阻抗定义为:
其中,V 是电压,可以通过在内外导体之间的任何一条线上取电场的路径积分来计算,P 是任意截面上的坡印廷通量的积分。我们可以使用积分耦合算子 来计算模拟域的边界和边的场,进而计算上述公式中的量。
定义一个单元模型
我们可以只考虑结构本身的一个周期部分,而不是计算波导的一个长段。但沿着波导传输的信号的有效波长将比这长得多,所以我们使用了 Floquet 周期边界条件来指定沿波导传输的波具有指定的传播常数。
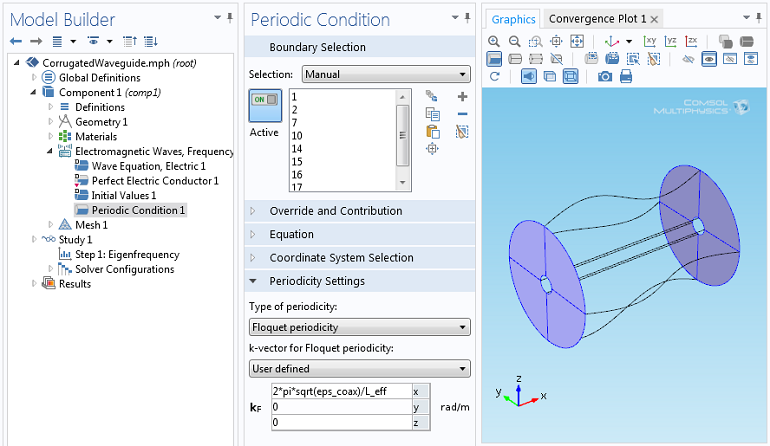
Floquet 周期边界条件界面。
通过这种方法,我们就可以求解一个特征值问题,计算出具有这个传播常数的波的频率。当使用周期性边界条件时,还需要确保边界上的网格是周期性的。
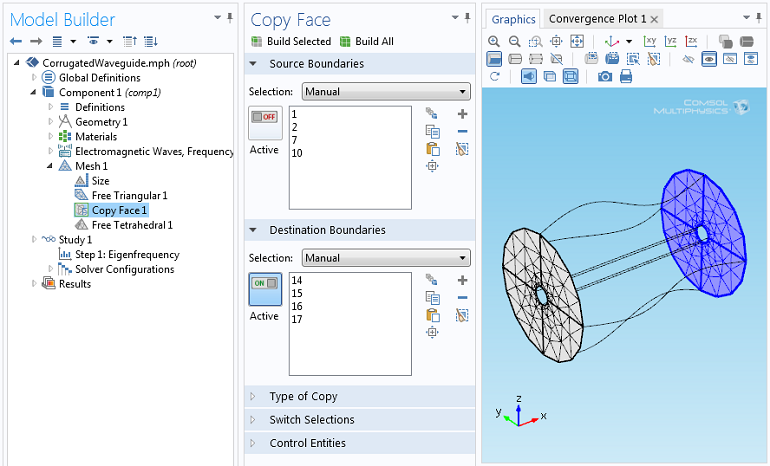
复制面功能将确保周期面上的网格是相同的。然后用自由四面体单元对内部进行网格划分。
只要计算出单个单元的解,我们就可以计算该频率下的阻抗。也可以在有效波长的范围内进行扫描,计算出一定范围内的阻抗,并观察到在更高的频率下,阻抗会上升。这意味着我们正在接近 TE 或 TM 模式将出现的频率。到那时,我们就不能再使用这种方法了。
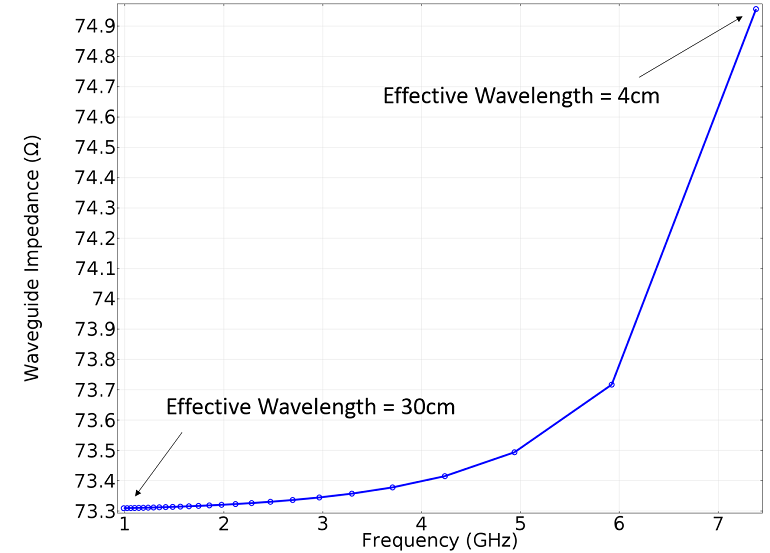
结语
在这篇博客中,我们通过一个案例教程展示了如何计算在准 TEM 系统中运行的具有周期性结构的波导阻抗。我们使用 Floquet 周期 边界条件和复制面 功能建立一个单元模型,通过求解该模型获得一段频率范围内的阻抗。
如果你对这种类型的建模有疑问,请联系我们。






评论 (0)