Menu
COMSOL 博客

线弹性结构刚度的计算：第 1 部分

Author Image
作者 Supratik Datta
2014年 4月 3日

今天，我们将介绍结构刚度的概念，并了解如何计算仅受机械载荷作用的线弹性结构的刚度。我们将重点探讨如何在不同的建模空间维度（0D 和 1D）中计算和解释它，以及哪些因素会影响结构的刚度。

什么是结构刚度？

当外力作用在一个弹性体上并试图使它变形时，弹性体会产生阻力抵抗外力。这种阻力被称为刚度。我们经常随口会把这个术语称作材料属性，而实际上，它可能是各种几何和材料参数的属性。在这篇博客中，我们将探讨这些材料属性。

在深入研究之前，我们需要从数学上定义刚度。假设有一个力 F0 作用在物体上，使物体变形一个量 u0。如果给物体施加较小的力 ΔF，使其发生非常小的变形 Δu，那么这两个量的比值就是力在作用点的刚度，用状态变量 F0 和 u0 表示。

这就是线性刚度 的定义，一般来说，它可以用在线性和非线性的力与位移曲线中。力-位移关系和线性刚度可以分别用以下方程进行数学表达：

F(u)=F_0+k(F_0,u_0)(u-u_0)
k(F_0,u_0)=\lim_{\Delta u \to 0}\frac{\Delta F}
{\Delta u}
=\left.\frac{\partial F}
{\partial u}
\right|_{F=F_0,u=u_0}

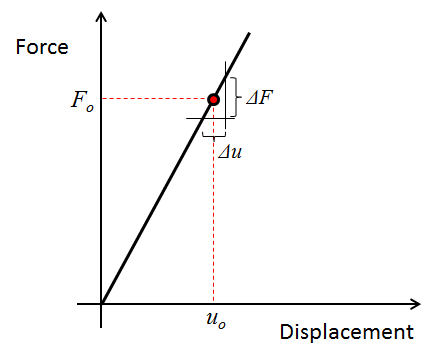
线弹性结构的力-位移曲线。
一个典型的线弹性结构的力与位移曲线。

一个实例问题

当对各种类型的结构系统进行建模时，分析的目标之一可能是计算出一个有效的刚度值，并根据计算方式来解释它的范围。一般来说，刚度可以是材料属性、材料方向、几何尺寸、加载方向、约束类型，以及施加了载荷和约束的空间域选择的函数。

为了便于说明问题，我们将使用长度 L=1m，宽度 b=0.2m，厚度 t=0.1m 的钢梁为例。该钢梁平行于 yz 平面且位于 x=0 的面是刚性固定的（即 x、y 和 z 方向的位移为零）。有一个均匀分布的力作用在与 yz 平面平行且位于 x=L 的面。梁的其他所有面是不受约束和无载荷的。因此，它们可以自由变形。

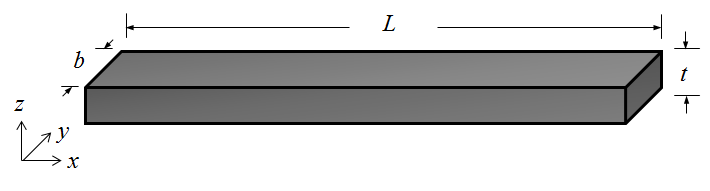
一个实体梁的示意图。
一根长为 L、宽为 b、厚为 t 的实心梁，边与直角坐标系的 x、y、z 方向对齐。

我们将通过解析法和使用 COMSOL Multiphysics 来计算该梁的刚度，并比较这两种方法得到的解。

探索建模空间维度

当开始对一个结构进行建模时，我们需要做出的一个关键选择是：决定我们真正感兴趣的细节有多少。换句话说，我们需要确定是否可以将整个结构作为空间中的一个点，或者是否需要在 1D、2D、甚至 3D 上求解它，来获得某些感兴趣的量的空间变化的更多细节。这意味着我们需要决定该结构可以被看作是一个单弹簧，还是一个分布在空间并相互连接的弹簧网络。

要做到这一点，我们应该尝试回答以下问题，可能还有其他几个问题，这取决于建模目标是什么：

  • 材料属性是否存在空间不均匀性？
  • 施加的力是否存在空间不均匀性？
  • 结构的几何尺寸在某些方向上是不规则变化的吗？
  • 是否有任何对称性的平面，让我们可以根据所建模的几何结构的对称性、施加的载荷和解的预期形态来确定？
  • 是否存在我们感兴趣的，如孔或角周围的局部效应？
  • 我们可以忽略某些方向上的应力或应变吗？

0D 模型中的刚度

我们首先查看梁的 0D 模型，在这个模型中，所有与加载、变形和材料响应有关的影响都被集总在空间的一个点上，整个梁被建模为单弹簧。

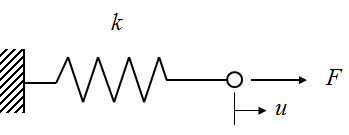
使用一个集总刚度表示0D的梁。
使用一个集总刚度 k，和一个作用在梁上并产生位移 u 的力 F，来表示 0D 的梁。在这种情况下，0D 模型也是梁的单自由度（SDOF）表示。

假设钢的行为遵循胡克定律（即应力与屈服强度以下的应变成比例），我们可以用材料的杨氏模量 E 写出应力-应变关系，即 \sigma=E\epsilon。

使用一个简单的定义，其中应力等于单位横截面积的力，\sigma=F/A，A=bt，应变等于变形与原始长度的比值，\epsilon=u/L，结合这些，我们得到 F=(EA/L)u。于是，我们得到力与位移的线性关系，使刚度与作用点以及力、位移和材料属性的任何空间变化无关。

因此，我们可以用以下公式来表达这个 0D 梁模型的轴向刚度：

k=\frac{EA}{L}

假设钢的杨氏模量为 200GPa，梁的轴向刚度为 k=4×109N/m。

在 COMSOL Multiphysics 中，您可以使用全局常微分方程和微分代数方程 接口（用于瞬态模拟）或简单地在零维模型中设置参数 或变量 来建立 0D 模型。

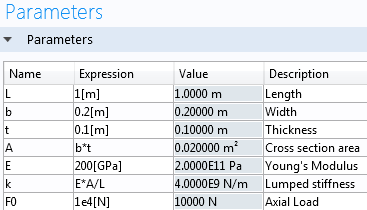
COMSOL 软件中的参数表的屏幕截图。
COMSOL 软件中的参数表的屏幕截图。

1D 模型中的刚度

在真实世界中，我们知道梁的一端是固定的，而另一端是受力的。因此，在沿长度方向的每个截面上的变形或位移（u）是不一样的。为了考虑这种影响，我们至少需要建立一个 1D 模型。

计算轴向刚度

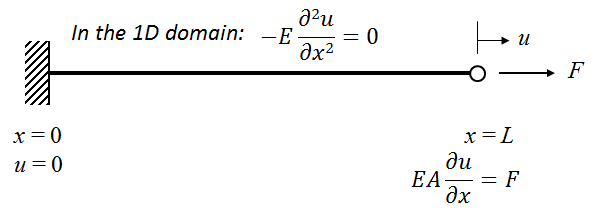
计算轴向力的示例：梁的1D表示。
使用轴向力的静力平衡得到的梁的 1D 表示。

1D 模型要求我们在 1D 域上求解代表梁的轴向力平衡方程，以找出定义 1D 空间的 x 坐标与轴向位移（u）的函数。轴向力平衡方程（忽略任何弯曲或扭转力矩）可以写成：

-E\frac{d^2u}{dx^2}=0

两端的边界条件分别为：u=0 ，x=0，E\frac{du}{dx}=\frac{F}{A}（胡克定律），x=L。

结合上述等式，我们得到 u(x)=\frac{Fx}{EA}，其中 x 是距梁固定端的距离，u(x) 是沿梁长度的位移。1D 模型表示无限多的弹簧相互串联在一起。这使我们能够得到关于梁的位移、应力和应变的空间变化的更详细的信息。它也可以理解为这些弹簧中的每一个都有自己的刚度。假设杨氏模量和横截面积不沿梁的长度方向变化，如果我们将梁离散成 n 个串联的弹簧，在我们的例子中，每个弹簧的刚度（ki ）将是 k_i=nEA/L。

然而，如果我们想把 1D 模型与 0D 模型联系起来，必须想象整个梁由一个弹簧近似。因此，1D 的等效刚度将是最大轴向位移与受力位置的轴向力之比。在这种情况下，u 在 x=L 处是最大的，其值为 u_{max}=FL/EA。于是，我们得到 1D 梁的等效单弹簧刚度：

k=\frac{EA}{L}

这表明，对于给定的建模参数，当在 x=L 处计算时，1D 模型的解（k=4×109N/m）接近 0D 模型的解。

计算弯曲刚度

转移到 1D 模型的另一个好处是，我们现在可以探索加载方向的影响。虽然我们将自己限制在 1D 空间内，但可以分别沿着“看不见的” y 和 z 方向计算平面外的位移 v 和 w，当一个力沿着这些方向作用在梁上时。请注意，基于所选择的边界条件（一端固定一端自由的梁），位移分量 v 和 w 将作为 x 坐标的函数而变化。

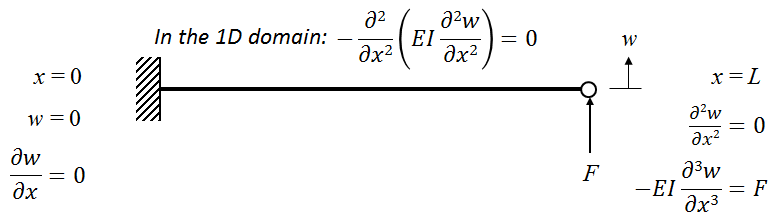
梁的1D表示。
使用弯矩平衡获得的梁的 1D 表示。

研究这种情况也意味着我们必须引入额外的刚度项，将弯曲力与平面外位移相关联。这就要求我们在 x=0 w=0 和 \frac{dw}{dx}=0 以及 x=L，\frac{d^2w}{dx^2}=0 和 -EI\frac{d^3w}{dx^3}=F 边界条件下，求解以下力矩平衡方程：

-\frac{d^2}
{dx^2}(EI\frac{d^2w}{dx^2})=0

在这些方程式中，我们将沿 Z 方向的位移（w）作为分析目标的代表。同样，将沿 y 方向的位移（v）作为分析目标的代表。假设变形比梁的尺寸小得多，这些表达式可以在物理上作如下解释。

平面外位移相对于 X 坐标的一阶导数代表斜率；二阶导数代表曲率；三阶导数与剪切力成正比。在这些方程中， I 项表示第二面积惯性矩，是梁弯曲方向的一个函数。对于围绕 y 轴的弯曲（即沿 Z 方向作用的力），我们可以将其表示为：

I_{yy}=\frac{1}{12}bt^3

对于围绕 Z 轴的弯曲（即沿 y 方向的作用力），我们可以表示为：

I_{zz}=\frac{1}{12}b^3t

结合所有这些表达式，我们可以得到：

w(x)=\frac{Fx^2(3L-x)}{6EI_{yy}}

因此，1D 的等效弯曲刚度为最大平面外位移与受力位置的弯曲载荷之比。在这种情况下，当沿 y 和 z 方向施加力时，v 和 w 在 x=L 处都将是最大的。因此可以得到两个可能等效的 1D 梁的单弹簧弯曲刚度，具体取决于加载方向。

沿着 Y 方向的力和位移可以用刚度 k_{yy}=\frac{Eb^3t}{4L^3} 关联。沿着 Z 方向的力和位移可以用刚度 k_{zz}=\frac{Ebt^3}{4L^3} 关联。对于给定的建模参数，kyy = 4×107 N/m，kzz = 1×107N/m。

在 COMSOL Multiphysics 中计算刚度

在 COMSOL Multiphysics 中，您可以先选择 2D 或 3D 空间维度，然后使用桁架 或梁 接口设置 1D 模型。

在这里，我们将向您展示如何在 3D 空间维度上使用梁 接口计算轴向和弯曲刚度。1D 结构将被建模为欧拉-伯努利（Euler-Bernoulli）梁。COMSOL 软件也允许使用铁木辛柯（Timoshenko）梁理论，它更适用于对低长宽比的结构进行精确 1D 建模。

下面是通过 1D 模型获得刚度的工作流程：

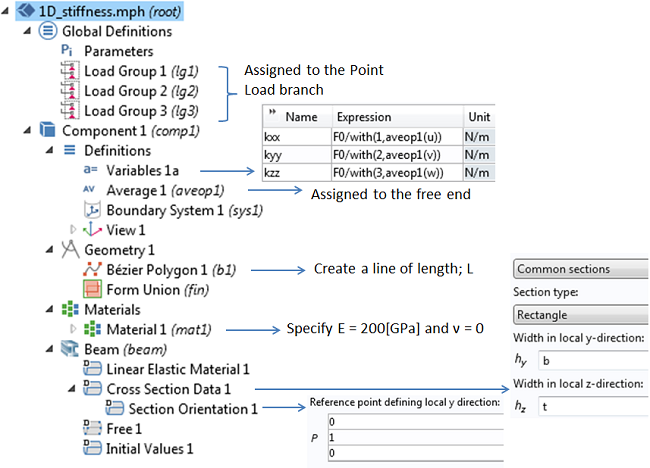
用于模拟轴向刚度和弯曲刚度的梁接口。
使用 梁接口建立的 1D 模型的屏幕快照。变量被定义为计算轴向刚度（kxx）和弯曲刚度（kyy 和 kzz）。平均耦合算子用于计算 x=L 点的位移。 with() 算子用于从模型求解的不同载荷工况下获取解。

梁接口的点载荷分量。
梁接口中使用的边界条件的屏幕快照。点载荷分量被施加给位于 x=L 的点。

在这个模型中，我们使用的力（点载荷）为 F0 = 1×104N。只要不在模型中加入任何非线性效应，就可以使用任意大小的载荷。如果存在非线性，那么使用正确的线性化点很重要。这种情况将在以后的博客中讨论。

如图所示，你可以使用 if() 算子和与载荷组 相关的名称（如 root.group.lg1）创建一个 “开关”，这样当你在几个载荷下求解同一个模型时，一次只能使力矢量的一个分量不为零。

COMSOL Multiphysics中用于分析线弹性结构的研究设置。
研究设置的屏幕快照，说明载荷是如何设置的，以便一次只激活力矢量的一个分量。全局计算用于输出 kxx，kyy，和 kzz 的值。COMSOL 软件的解与解析解完全匹配。

只要我们不期望拉伸和弯曲之间有任何耦合（即，当刚度矩阵是对角线时），这里显示的用于计算刚度组件的方法就适合。我们将在本博客系列的第 2 部分介绍一种更普遍的计算方法。

接下来，我们可以用铁木辛柯梁理论来求解同一模型。与我们的预期一致，模拟产生了与轴向刚度完全相同的结果（kxx = 4×109 N/m），但横向刚度将小于我们基于欧拉-伯努利理论得到的结果。在使用铁木辛柯梁理论时，考虑到的剪切变形将通过剪切模量对泊松比有轻微的依赖性，所以我们也需要将其纳入材料数据中。

泊松比 kxx[N/m] kyy[N/m] kzz[N/m]
ν = 0 4×109 3.91×107 9.94×106
ν = 0.3 4×109 3.88×107 9.92×106

结束语

在这篇博客中，我们介绍了使用解析法和 COMSOL 计算 0D 和 1D 线弹性结构刚度的方法。接下来的一篇博客，我们将讨论 2D 和 3D 情况。

编者注：我们在 2014 年 4 月 4 日发表了这个主题的后续博文。阅读本博客系列的第 2 部分，了解如何计算 2D 和 3D 的线弹性结构的刚度。

博客分类

相关主题

评论 (0)

正在加载...
浏览 COMSOL 博客
类别
标记