快速傅里叶变换 (FFT) 是一种有效且强大的数值方法。COMSOL Multiphysics ® 软件最新 6.0 版本增加了与此方法有关的新功能:空间 FFT 特征。在这篇博客中,我们将讨论如何使用这一新功能模拟光学应用,并展示一些应用案例。
术语和定义
首先,让我们来明确一些术语和定义的涵义。有三个术语需要区分:傅里叶变换 (FT)、离散傅里叶变换 (DFT) 和 FFT。函数 u 的傅里叶变换由下式定义
式中,x 和 \xi 分别是物理空间和傅里叶空间中的变量。当物理空间变量为时间 t 时,变量 \xi 称为频率。在光学领域,\xi 被称为空间频率,通常与波长和焦距成比例(我们将在下文讨论),而 x 是用于描述所关注的光学结构附近位置的物理空间坐标。
在之前的博客:如何在 COMSOL Multiphysics 中实现傅里叶变换和如何由计算解实现傅里叶变换中,我们讨论了如何在 COMSOL® 中实现傅里叶变换。我们可以使用一种数值方法实现傅里叶变换,即基于辛普森法则的直接数值积分。下文,我们将其称为“通过数值积分实现的傅里叶变换”。
离散傅里叶变换是傅里叶变换的离散形式,是对一组离散的点进行运算。它在 COMSOL ® 中的定义为
FFT 是计算 DFT 的一种有效算法。
请注意,上述傅里叶变换和离散傅里叶变换的定义是最通用的定义,但符号约定与 COMSOL 的波动方程,即 \exp(i(\omega t-{\mathbf k}\cdot{\mathbf x})) 的符号约定 不一致,。当使用这些符号定义弗劳恩霍夫和菲涅耳衍射公式时,请注意不要弄错。符号不一致并不影响稳态解。
如何使用空间 FFT 功能
接下来,我们来演示如何在光学应用中使用 COMSOL® 空间 FFT 功能模拟光学应用。FTT功能可以通过步骤 1 和 2 设置和实现:
- 步骤1:准备数据集
- 右键单击数据集 → 更多数据集 添加空间 FFT 数据集(定义傅里叶空间)
- 选择合适的源数据集作为物理空间,然后进行变换
- 将空间分辨率 设置为手动
- 将采样分辨率 设置为适当的数字
- 从空间布局 中选择使用补零,并将 x 填充 设置为适当的数字
- 在傅里叶空间变量 中选择频率
- 取消勾选屏蔽 DC
- 步骤2:使用
fft()算子绘图- 在绘图设置中调整 x 轴数据的空间频率比例
矩形函数示例
矩形函数是光学应用中最常使用的函数之一,因为它代表了一个硬边光阑。当存在硬边光阑时,总是涉及矩形函数的傅里叶变换。矩形函数的傅里叶变换可以很容易地通过手动计算,如下所示:
\begin{cases}
0 & |x|>a/2 \\
1 & |x|\le a/2
\end{cases}
式中,\mathcal F 代表傅里叶变换算子,a 是一个常数,{\rm sinc}(x) = \sin x/x 是 sinc 函数。
让我们看看如何在 COMSOL® 中使用 空间 FFT 功能计算此傅里叶变换。
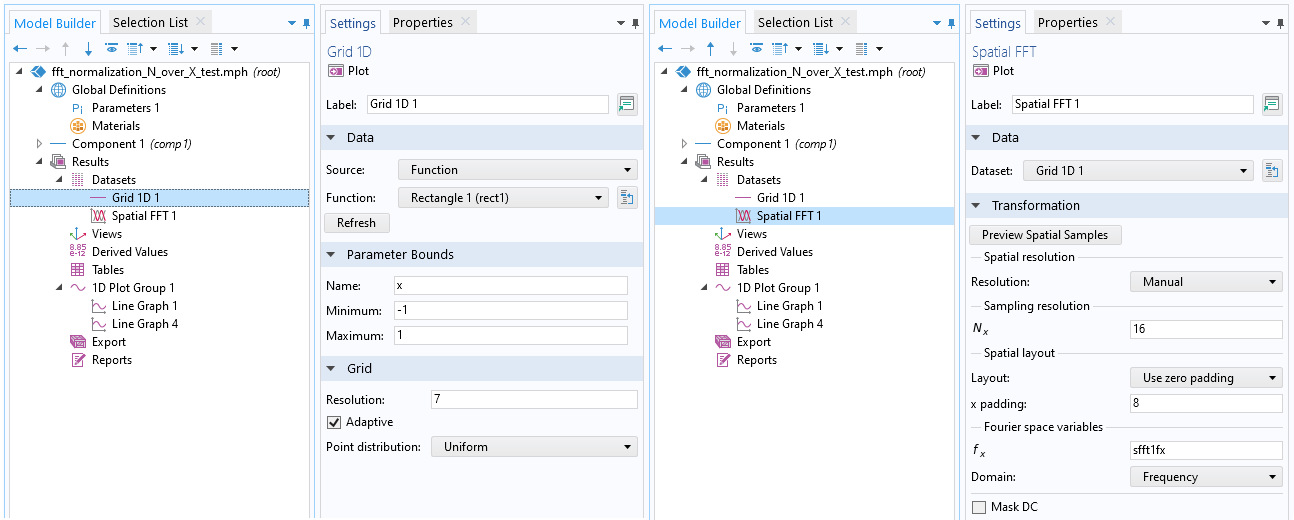
矩形函数内置于 定义 >函数 下。点击 创建绘图 按钮,结果下的 数据库 节点将为该函数自动创建一个新的数据集。 默认情况下,范围和分辨率也是自动设置的。在进行 FFT 时,自己控制这些参数很重要。傅里叶空间分辨率由物理空间范围的倒数和物理空间数据的零填充确定。傅里叶空间范围由物理空间范围和傅里叶空间采样数决定。FFT 结果的大小因物理空间范围和傅里叶空间采样数而异。下表是 FFT 参数表达式的汇总,包括与上图中显示的FFT 设置对应的参数值。
| 参数 | 表达式 | 示例值 |
|---|---|---|
| 实际上的总范围 | X_0 | 2 |
| 傅里叶空间采样数 | N_x | 16 |
| 补零 | N_z | 8 |
| 傅里叶空间总范围 | N_x/X_0 | 8 |
| 傅里叶空间分辨率 | \frac{N_x}{X_0} \cdot \frac{1}{N_x+2N_z} | 1/4 |
| 傅里叶变换归一化因子 | X_0/N_x | 1/8 |
进行上述设置后,矩形函数 rect1(x) 如下图所示,其傅里叶变换的绝对值 abs(fft(rect1(x)) 由 FFT 功能计算。傅里叶空间总范围是 N_x/X_0 = 16/2 = 8,即从 -4 到 4。可以看到傅里叶空间的采样点总数为 N_x+2N_z = 32。
为什么是 2N_z? 因为在补零中,N_z 零被添加到物理空间数据的两侧。傅里叶空间分辨率为 8/32 = 0.25。在没有归一化的情况下,FFT 运算结果因子为 N_x/X_0。所以,我们需要将结果乘以X_0/N_x 获得一个单位峰值。稍后,我们将对各种公式进行快速傅里叶变换,每个公式都有不同的乘法常数。因此,我们必须将 FFT 结果归一化。
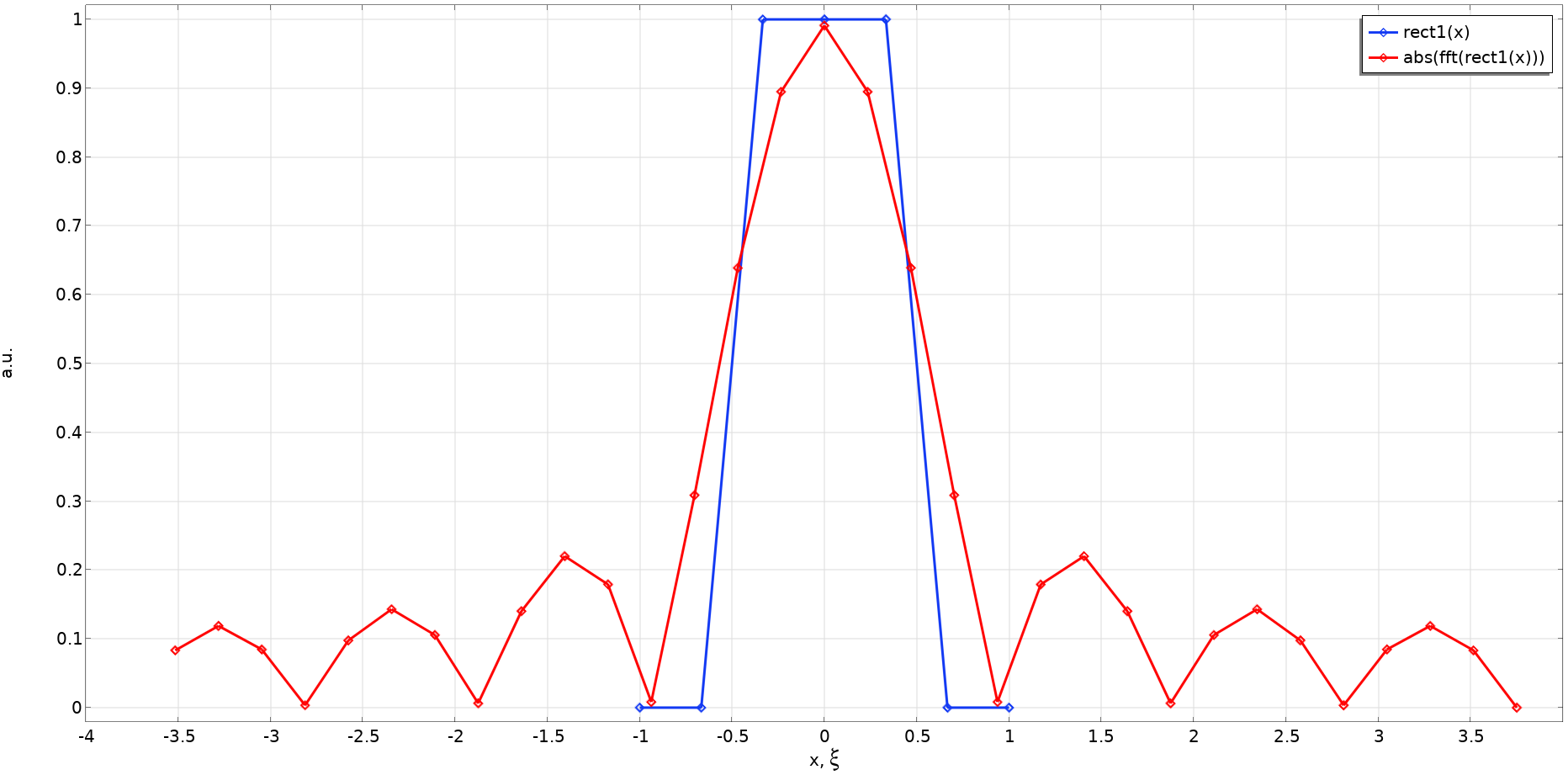
矩形函数 a = 1 及其 傅里叶变换 的绝对值,由 FF 和上述设置确定。
在这个示例中,我们有意将采样数设置为较低的数字,以便可以参考前面的公式。不过,仍然可以看到傅里叶变换,{\rm sinc}(\pi \xi) 是通过近似值计算得出的。使用更加合适的参数,例如 X_0 = 3,N_x = 128 和 N_z = 512,可以得到理想的结果,如下图所示。将通过数值积分计算的傅里叶变换结果叠加以进行比较。当然,这两种方法的结果应该一致!
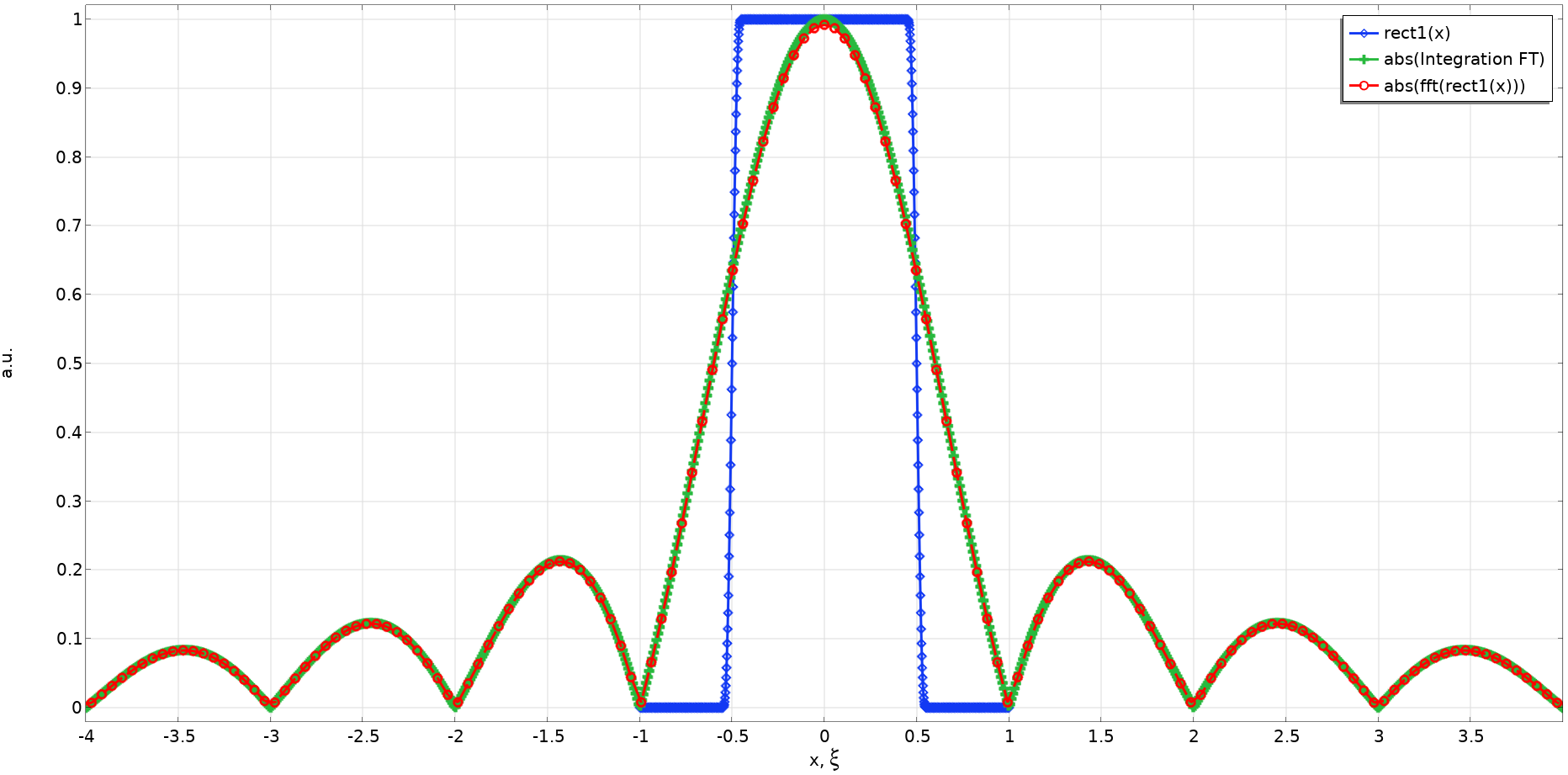
a=1 时,由高分辨率的 FFT 确定的矩形函数的傅里叶变换绝对值和由数值积分确定的傅里叶变换绝对值的对比
在光学应用中进行傅里叶变换
至此,我们已经了解了如何为矩形函数(一维解析函数)设置和使用 空间 FFT 功能。接下来,我们来看如何在一些实际光学应用示例中使用此功能。
在光学领域,将光电场的时间信号与其光谱(频率或波长)相关联的时频傅里叶变换可能更为大家所熟知。空间傅里叶变换被广泛应用于各种传播(变换)方法中,用于描述电场从一个平面传播到另一个平面的过程。在这个例子中,空间傅里叶变换将一个平面中电场的空间形状与另一个平面中的形状(称为空间频率)相关联。考虑一个入射到平面中扰动上的标量电场或矢量电场的分量,例如一个光圈或透镜,到达另一个平面,例如焦平面或像平面,如下图所示:
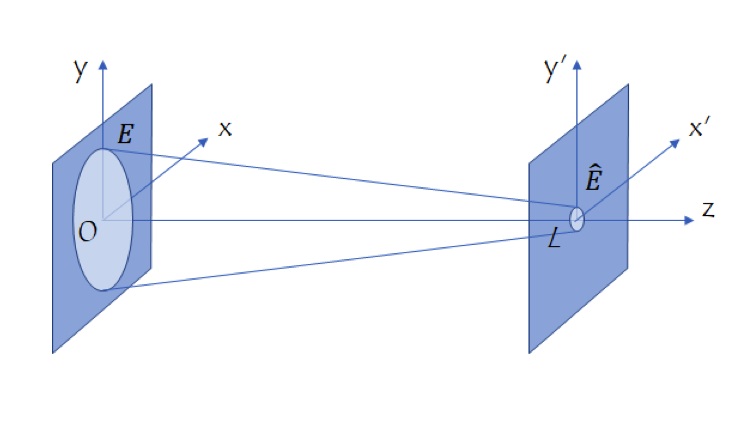
光学应用中传播(变换)方法的坐标系。
让我们来表征扰动后平面内的电场 E(x,y,0)。然后,根据不同的目标,使用四种传播方法中的一种来计算了另一个平面的电场 \hat{E}(x’,y’,L)。下表总结了四种方法。这些公式由傅里叶变换的简单相位函数符号 \mathcal{F}[\cdot] 表示。
| 理论 | 公式(简单符号) | 应用 |
|---|---|---|
| 1. 夫琅禾费衍射理论 | \hat{E}(x’) = {\mathcal F}[E(x)] | 夫琅禾费衍射条件下的标量远场——观察者距离衍射物体*很远,用于孔径、光栅和傅里叶光学等应用。 |
| 2. 菲涅耳衍射理论 | \hat{E}(x’) = {\mathcal F}[E(x)\exp(-ikx^2/(2L))] | 菲涅耳衍射条件**下的标量近场至远场,适用于低数值孔径 (NA) 透镜系统等应用。 |
| 3. 角谱法*** | \hat{E}(x’) ={\mathcal F}^{-1}[{\mathcal F}[E(x)]\exp(ik\sqrt{1-\alpha^2})] | 适用于任何系统(例如高数值孔径透镜系统)的严格单向标量场解决方案(不考虑反射)。 |
| 4. 部分相干理论(Schell 模型)**** | I_{pc}(x’,L) = {\mathcal F}^{-1}[{\mathcal F}[I_c(x)] {\mathcal F}[\gamma(x)]^\ast ] | 非干扰或低干扰光源,例如 LED 和太阳光,使用在在夫琅禾费或菲涅耳衍射近似下的互相干函数的 Schell 模型假设。 |
脚注:
* 夫琅禾费衍射条件
** 菲涅耳衍射条件
*** \alpha 是方向余弦
**** I_{pc}是部分相干强度,I_c 是相干强度,并且 \gamma 是互相干函数
夫琅禾费衍射
夫琅禾费衍射公式用于计算满足夫琅禾费条件时,从物体衍射的远场。
以下是完整的公式:
(x’,y’,L) = \frac{e^{i k L}}{i \lambda L} \iint_{-\infty}^{\infty}E(x,y,0) e^{-i 2\pi (x’ x+y’ y) / (\lambda L)}dxdy
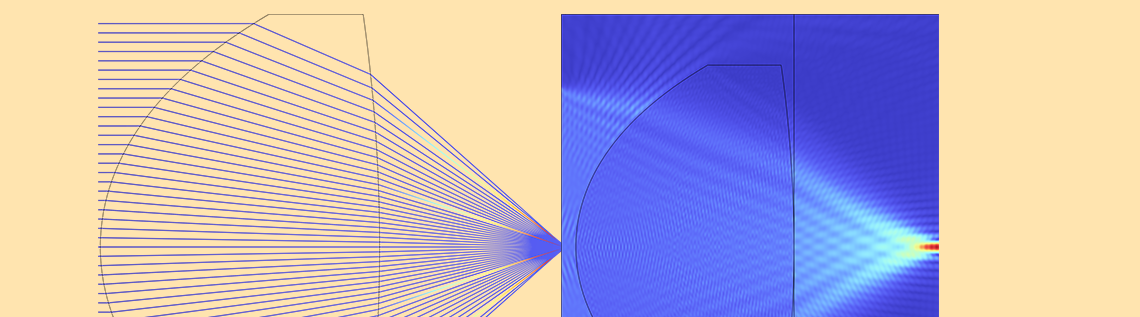
该公式用于计算孔径、光栅的远场和傅里叶光学焦平面内的场(参考文献 1)。该物体是一个具有均匀光照的方形孔径。孔径出口平面的电场是一个二维矩形函数,远场由 FFT 计算。这会形成一种熟悉的衍射图案,类似于从网状窗帘后面观察路灯时的景象。请注意,我们需要将图中的 x 轴数据缩放为 \lambda L,因为空间频率被缩放为 f=x’/\lambda L。 通过数值积分使用傅里叶变换计算二维傅里叶变换需要的时间较长,但 FFT 可以非常快速地完成这项工作。
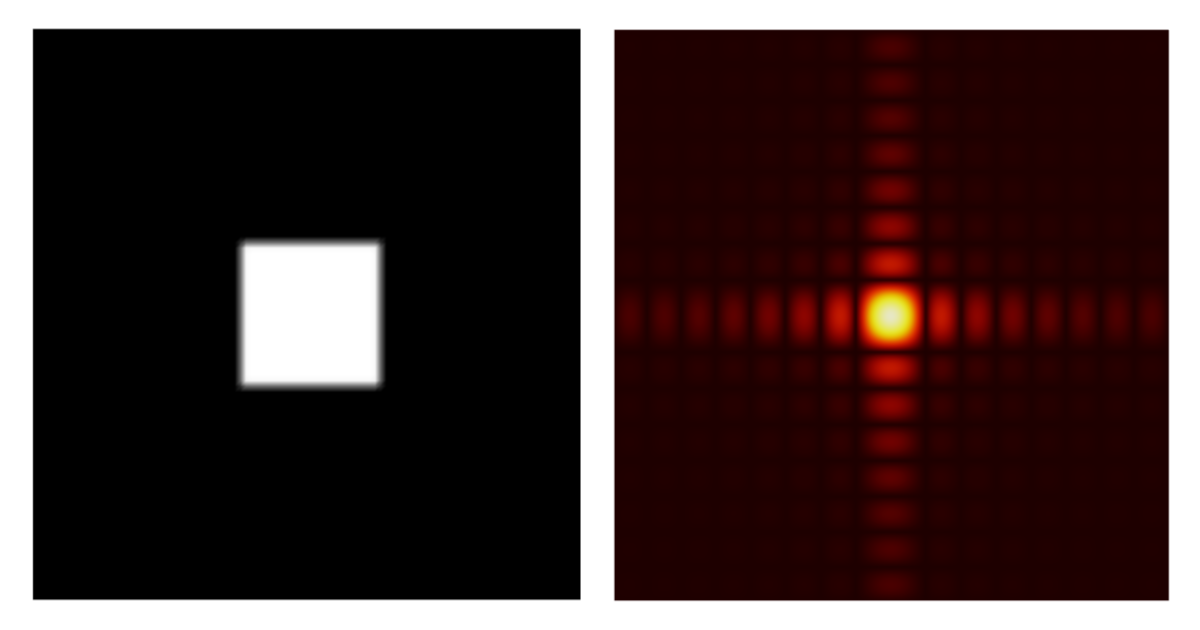
方形孔径(左)及其衍射图案(右)。
模拟方形孔径的设置非常简单:
菲涅耳衍射
第二个应用,菲涅耳衍射公式,可用于计算远场以及近场干扰。这个近似值的完整公式为:
(x’,y’,L) = \frac{e^{ikL}}{i\lambda L}e^{ik(x’^2+y’^2)/(2L)}\iint_{-\infty}^{\infty}E(x,y,0)e^{-ik(x^2+y^2)/(2L)} e^{-i 2\pi (x’ x +y’ y)/ (\lambda L)}dxdy
请注意,x 轴数据需要按因子 \lambda L 进行缩放。菲涅耳透镜模型应用了这种方法,通过 波动光学,频域 接口计算透镜内部的电场。基于菲涅耳衍射公式通过数值积分进行傅里叶变换计算焦平面中的场。如下图所示,可以在该模型中使用 FFT 功能,并通过数值积分得到与傅里叶变换相同的结果。
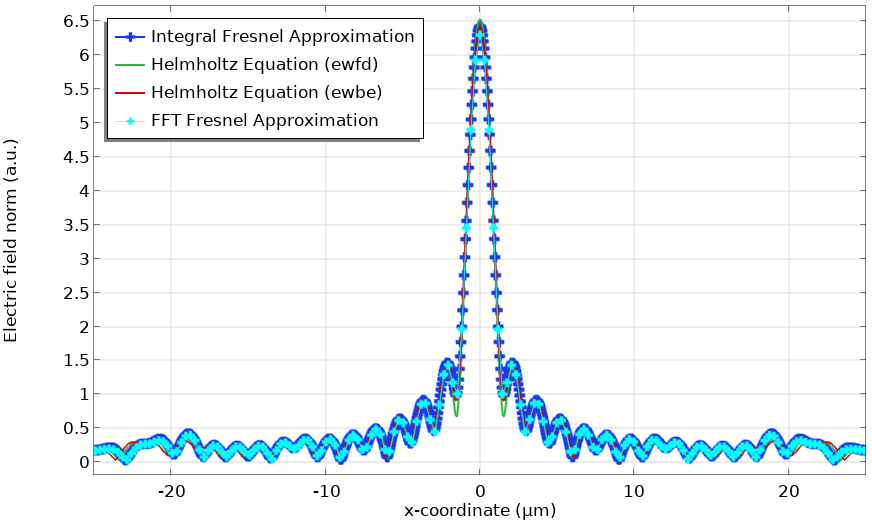
菲涅耳透镜模型焦平面中的电场模。FFT 功能用于计算菲涅耳衍射公式,并与其他方法进行比较。
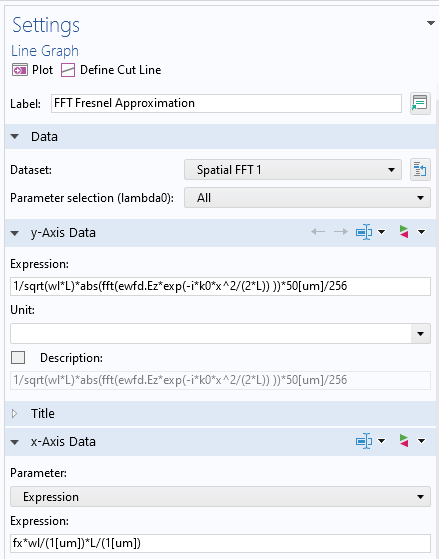
用于菲涅耳衍射公式的 FFT 功能的后处理设置。请注意,y 轴数据是标准化的,x 轴数据是按比例缩放的。
角谱法
第三个应用,角谱法,实现起来有点麻烦,因为它需要进行两次傅里叶变换,由其完整公式可以看出:
A \left(\frac{\alpha}{\lambda},\frac{\beta}{\lambda},0\right) e^{ikL\sqrt{1-\alpha^2-\beta^2}} e^{i2\pi (\alpha x+\beta y) /\lambda} d\frac{\alpha} {\lambda} d\frac{\beta}{\lambda}
,
式中,
,0\right) = \iint_{-\infty}^{\infty} E(x,y,0) e^{-i2\pi (\alpha x + \beta y)/\lambda} dxdy,
\alpha 和 \beta 是方向余弦。
在上文提到的博客中,我们介绍了如何模拟大型光学器件;即可以使用 波动光学,频域 接口计算光学元件周围的小域,然后使用 弗劳恩霍夫或菲涅耳衍射公式,或者使用 波束包络 接口模拟整个域。然而,这两种方法仅适用于慢速(低 NA)透镜,因为快速(高 NA)透镜需要大量网格单元,而夫琅禾费和菲涅耳公式无法给出很好的近似值。波矢太陡,波束包络 接口无法对计算域进行网格划分。
模拟大型高数值孔径透镜的唯一方法是使用角谱法(ASM)。这是一种与夫琅禾费和菲涅耳衍射公式属于同一类型的数值传播方法。只要知道一个平面中的场,即可计算另一个平面中的场。角谱法非常严格,因为它满足亥姆霍兹方程。可以结合波动光学模块使用该方法计算某个域中的场,然后使用角谱法将场传播到更远的平面。
下图中是一个高 NA 透镜 (NA=0.66) 的示例,它比 DVD 拾取透镜快得多。透镜半径为 16μm,后焦距(透镜第二面与焦平面之间的距离)为 10μm。结合使用 几何光学 接口与优化模块,对该透镜头进行了优化,使其在 0.66μm 的波长下具有衍射极限。透镜被特意设计得很小,使波动光学,频域 接口可以计算出严格的解以进行比较。我们将演示如何使用角谱法将场从该透镜的出射面传播到焦平面。
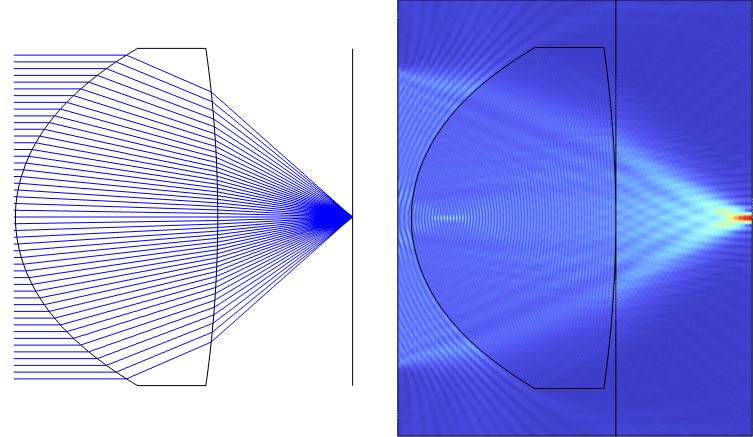
使用射线光学模块和优化模块(左)设计的 NA=0.66 透镜。使用 波动光学,频域接口(右)模拟的透镜的全波模拟。注意代表透镜出射平面的线,场从该平面传播到最右边的边缘,即焦平面。
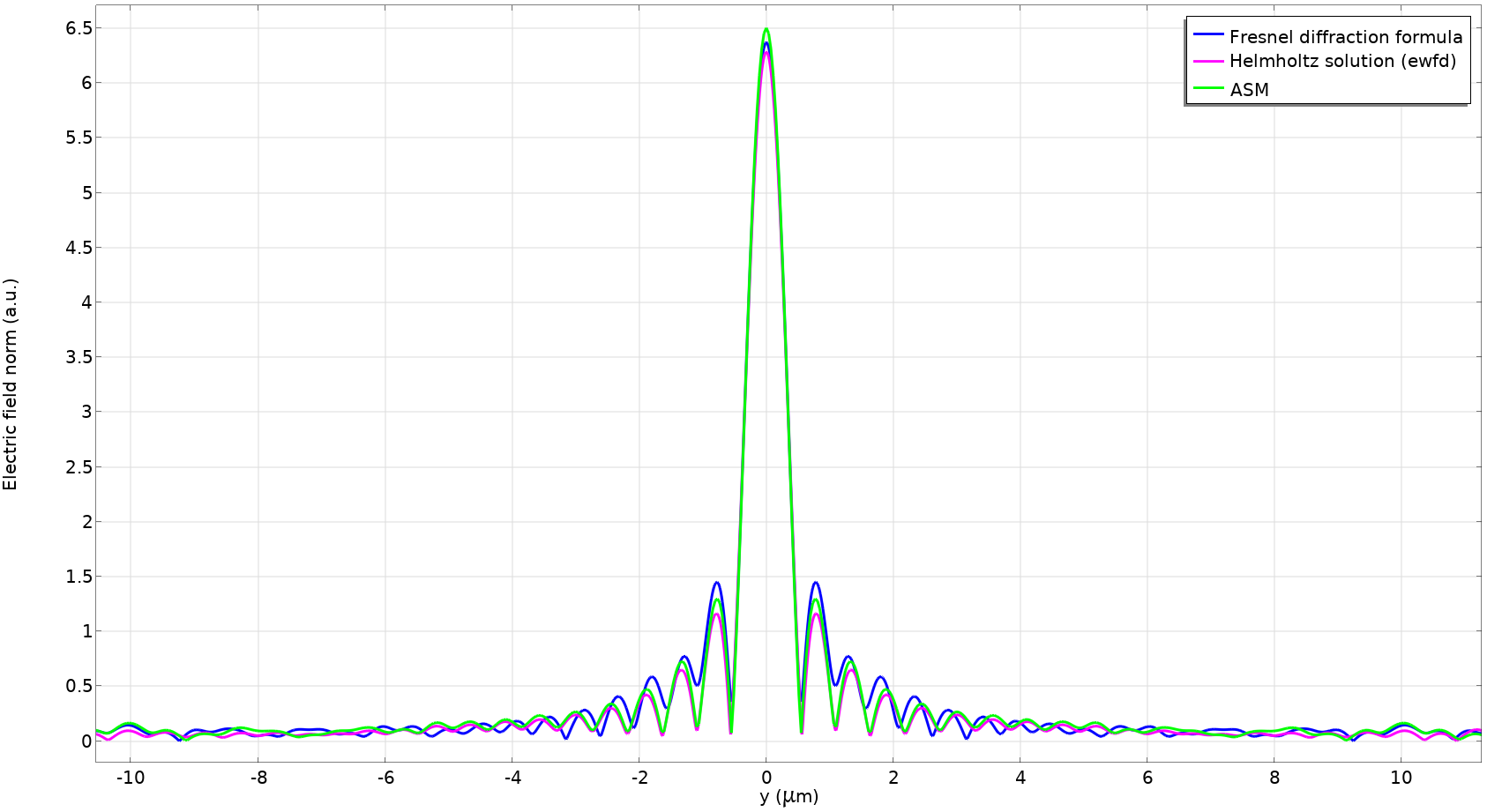
NA=0.66 透镜光斑轮廓模型与使用菲涅耳衍射公式计算的结果比较;由 波动光学,频域 接口计算的严格解;和使用角谱法计算的结果。请注意,对于这个透镜,菲涅耳衍射公式不再准确。(为了更好地进行比较,显示了 11μm 而不是 10μm 处的光斑轮廓。)
为了进行两次傅里叶变换,我们需要将第一次傅里叶变换存储在数据集中。这是因为 fft() 算子只是一个后处理算子,不是可以在物理设置中使用的通用算子,如 integrate算子。在当前版本的 COMSOL Multiphysics 中(在未来版本中,fft() 算子将被提升为通用算子),我们仍然需要在第一次傅里叶变换的物理场设置中通过数值积分来使用傅里叶变换,然后将 fft() 算子用于后处理中的第二次傅里叶变换。边界常微分和微分代数方程 与分布式常微分方程 节点的接口被定义在透镜出射平面上,通过数值积分傅里叶变换执行第一次傅里叶变换,并将结果存储为函数 u,如下图所示:
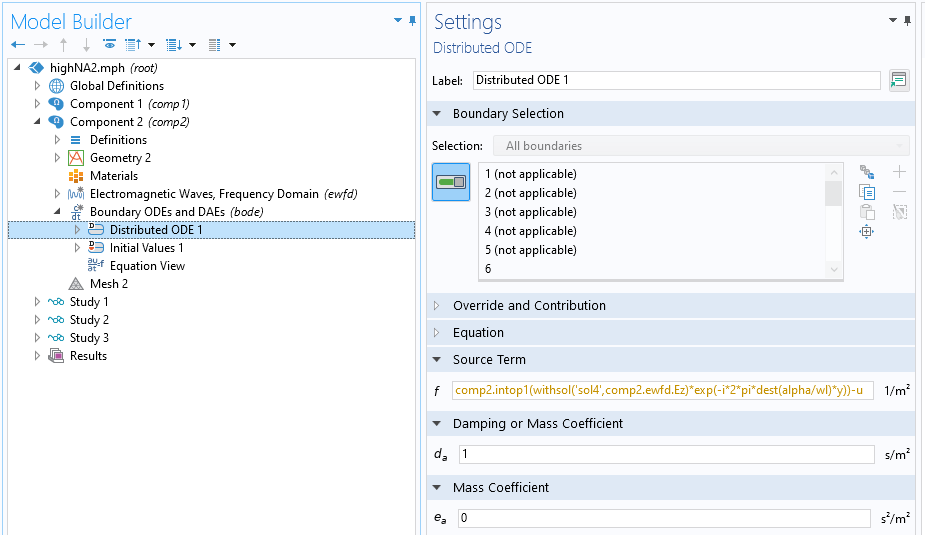
使用角谱法时,第一个傅里叶变换的 边界常微分和微分代数方程设置的屏幕截图。请注意,我们通过透镜半径 D/2 对傅里叶空间进行了归一化,进行适当的缩放。
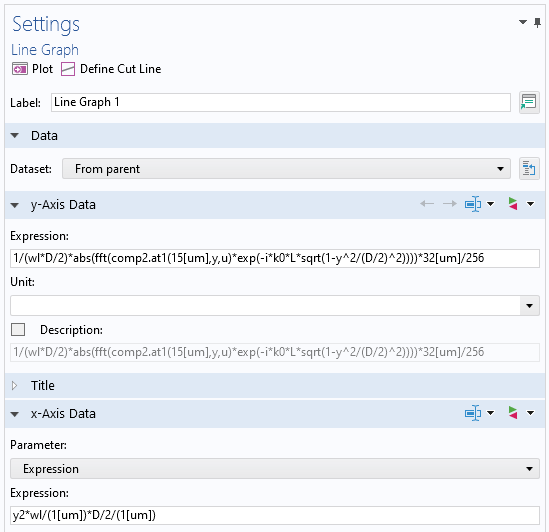
使用角谱法时,在后处理中进行第二次傅里叶变换的设置窗口屏幕截图。对于第二次傅里叶变换,注意方向余弦 a 在 y 轴数据中由归一化的 y 坐标表示,\alpha = y/(D/2),x 轴数据中的归一化因子 1/wl 来自变量的微分 d(\alpha/\lambda)。另请注意,空间频率名称 y2 是在 空间 FFT 数据集中任意选择的。
值得一提的是,第二次傅里叶变换其实就是逆傅里叶变换,但是傅里叶变换的绝对值和逆傅里叶变换到常数之间没有区别。我们已经看到,使用角谱法给出了一个与亥姆霍兹解一样准确的结果,因此可以将这种方法用于其他高 NA 透镜系统,例如大型高 NA 菲涅尔透镜。
结束语
在这篇博客中,我们了解了设置 空间 FFT 特征的基础知识,以及如何在一些重要的光学应用中使用此功能的示例。在本系列的下一篇博客中,我们将讨论第四个应用,即部分相干光束计算(使用的公式与文中第三个应用使用的公式相同)。
参考文献
- J. W. Goodman, Introduction to Fourier Optics, 3rd ed., Roberts and Company Publishers, 2005.
- M. Born and E. Wolf, Principles of Optics, 7th ed., McGraw-Hill, 1968.
- A. C. Schell, “A technique for the determination of the radiation pattern of a partially coherent aperture,” IEEE Trans. Antennas Propag., vol. 15, no. 1, pp. 187–188, 1967.






评论 (3)
晓工 王
2022-11-29为什么空间FFT在变换过程中预览空间样本总提示数据集类型无效?另外在输出时为什么提示fft为未知函数呢?
坤 何
2024-06-02什么时候能出一个完整的模型呢
Min Yuan
2024-06-03 COMSOL 员工您好,目前建议根据博客介绍来帮助设置模型,关于后续更新或示例演示,建议持续关注官网相关内容。