
Oldroyd-B 数值模型定义了在应变下表现出复杂黏弹性行为的流体中的流动,例如黏土、牙膏、油和聚合物溶液。本文介绍了如何使用 COMSOL Multiphysics 软件和附加的 CFD 模块求解 Oldroyd-B 流体的基准模型,其结果已经被已发表的研究所验证。
Oldroyd-B 模型定义了黏弹性流体行为
我们可以将 Oldroyd-B 模型写成一个方程,用以下变量描述黏弹性流体的行为:
- 应力张量
- 弛豫时间
- 延迟时间
- 应力张量的上随体导数
- 流体速度
- 由溶剂和聚合物组成的总黏度
- 变形率张量或应变率张量
尽管模型看起来很简单,但由于涉及到复杂的流体动力学,在许多情况下,对于数值模拟可能是一个挑战。这就是 COMSOL 软件发挥作用的地方。
Weissenberg 数和最小二乘稳定性
无量纲的 Weissenberg 数将 Oldroyd-B 流体中的弹性力和黏性力进行比较。在简单的情况下,例如稳态剪切流,这个数字是通过剪切速率乘以弛豫时间得到的。
关于流体的行为,Weissenberg 数表明了什么?
- 0 表示流体是纯黏性的
- 对于 Oldroyd-B 流体,大于 1 被认为弹性力是较高的
- 无限大意味着流体具有纯弹性响应
我们知道 Weissenberg 数对于分析 Oldroyd-B 流体很重要,那么是什么使我们无法得知它呢?Weissenberg 数本质表现出很强的对流特性。这意味着随着流体弹性的增加,溶液变得更加不稳定。
本教程中的材料模型是使用基于方程的建模来定义的,因为在 CFD 模块中还没有 Oldroyd-B 接口。因此必须手动添加使数值解稳定的最小二乘稳定项方法。这样做提高了解的稳定性,并使我们能够在解变得不稳定之前在更大范围的 Weissenberg 数内找到解。
黏弹性流体的数值模拟
Oldroyd-B 基准的几何结构由两个平行板之间的圆柱体和具有二维流动的 Oldroyd-B 流体组成。需要注意的一项规范是,圆柱体的半径和通道的半宽之间的宽高比为 1:2。此外,计算域被设置为半宽的 40 倍长,这样可以避免入口和出口的影响。
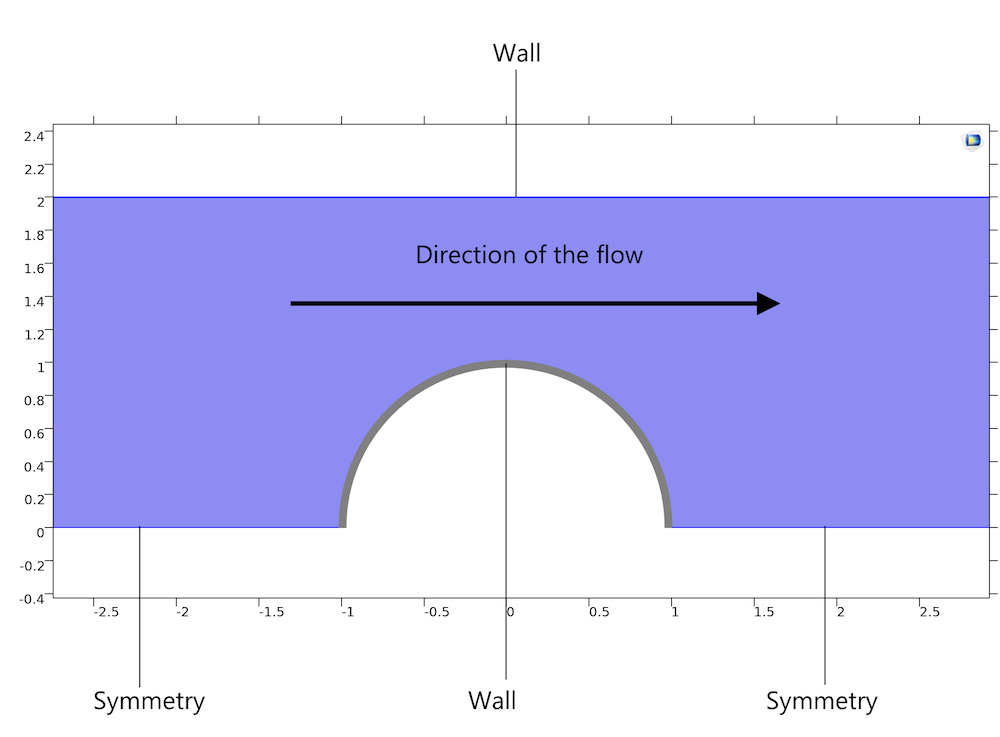
描述黏弹性行为的 Oldroyd-B 流体流动模型示意图。
该模型包括以下边界条件:
- 对称,所以只需要模拟通道和圆柱体的上半部分
- 壁上的无滑移边界
- 半入口,具有充分发展的抛物线速度分布和相应的额外应力分量
- 出口的压力分布考虑了充分发展流动的影响
通过参数化求解模型,我们可以逐渐将 Weissenberg 数从 0 增加到 1。如下图所示,COMSOL 软件将 Oldroyd-B 模型的 Weissenberg 数求解为典型值 0.7 Wi。模拟结果给出了通道内的流场和应力分布,以及流体的阻力系数,它是 Weissenberg 数的函数。
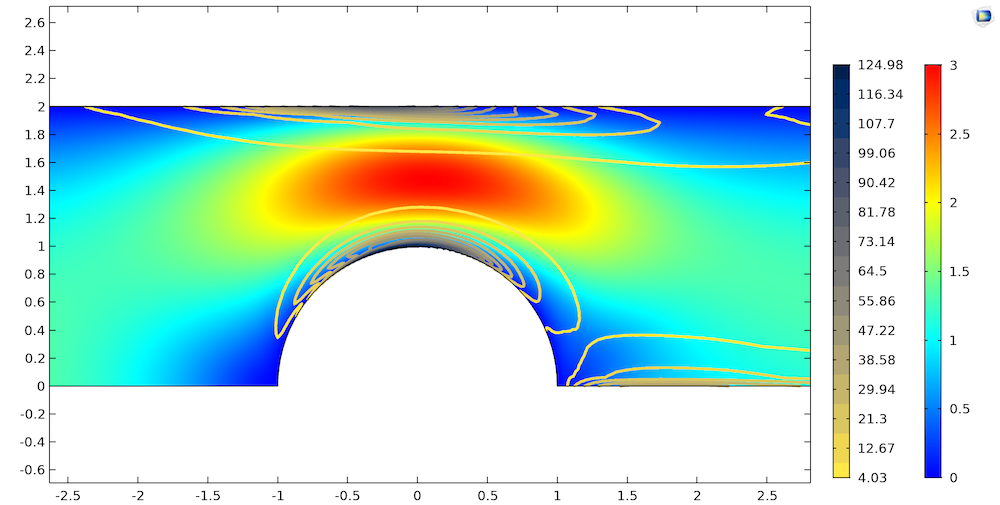
流场(Rainbow 颜色图例)和通道中 Oldroyd-B 流体的 T11 应力(Cividis 云图等高线)。
Oldroyd-B 流体模型的模拟结果与文献中公布的实验结果非常一致,这验证了 COMSOL Multiphysics 和 CFD 模块在黏弹性流动数值模拟中的应用。
后续步骤
尝试自己动手求解 Oldroyd-B 模型:点击下面的按钮,你将进入 COMSOL 案例库,并可以下载一个逐步讲解的指南和 MPH 文件。
了解有关可用功能的更多信息请查看:使用 CFD 模块模拟流体流动应用。






评论 (4)
乐帅 梁
2024-11-23这个模型如何进行参数化扫描?
越 赵
2024-11-28 COMSOL 员工您可以在研究上右键选择参数化扫描,然后设置需要扫描的参数和参数范围,点击计算即可。
jian tao
2025-03-27请问这个模型基于方程的建模,手动添加使数值解稳定的最小二乘稳定项方法,相应的案例模型有吗?目前6.1-6.3中没有基于方程的建模案例了呢?
越 赵
2025-04-07 COMSOL 员工COMSOL目前支持直接使用现成Oldroyd-B 模型来求解黏弹性流动,会更加的方便易用。目前开放的6.1-6.3中已经没有基于方程的建模案例了。