电池放电过程中,电路中的电流从正极流向负极。根据欧姆定律,这个过程中电流与电场强度成正比。但是,电池内部是什么情况?电流是从负电势流向正电势吗?这篇博客,我们将解释电池放电和充电过程中其内部的电势分布情况。
电池中的电流
我还记得在学校物理课上学习电气系统时,由欧姆定律了解到,电流从正电势流向负电势,电子的移动方向则相反;由基尔霍夫定律可知,电流必然具有连续性,即电流不会从系统中“消失”。但是,当研究电池内部结构中的正极、负极和隔膜中的电解质时,老师也很难解释电池放电过程是如何遵循这两个定律的,或者学生们无法理解。
图 1显示了上文提到的难题。我们知道,在放电过程中,电流 I 在外部电路中从正极流向负极。那么,在电池内部,电流是否从负极流向正极呢?还是说电流在电池内部并不保持连续性?答案或许显而易见:仅依据欧姆定律是无法解释电池内部发生的情况。当时对年轻学生而言是个谜的问题,现在可以用双电层理论来解释清楚。
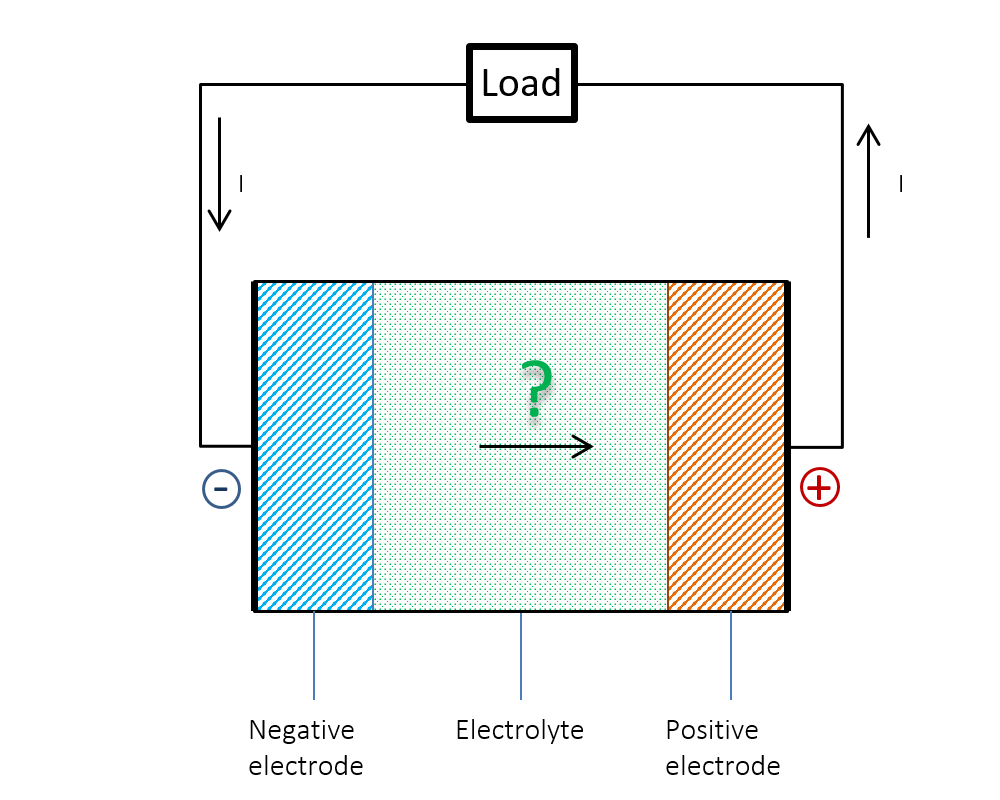
图 1. 电池内部的电流是否从负极流向正极?
电池内的双电层结构
当我们把金属条浸入电解质(例如盐溶液)中,会出现什么情况?受金属的类型和结构的影响,离子会被吸附在金属与电解质的界面处。紧贴金属的第一层通常是溶剂分子,不过一些没有溶剂包裹的离子也可能与金属表面直接接触并被吸附。请注意,在这种情况下,负离子会接触并被吸附在带负电的表面上。由溶剂分子和接触吸附的离子组成的物质层被称为内亥姆霍兹平面(IHP),如图 2所示。与金属表面电荷相反的溶剂化离子可能会形成另一个外层,称为外亥姆霍兹平面(OHP)。
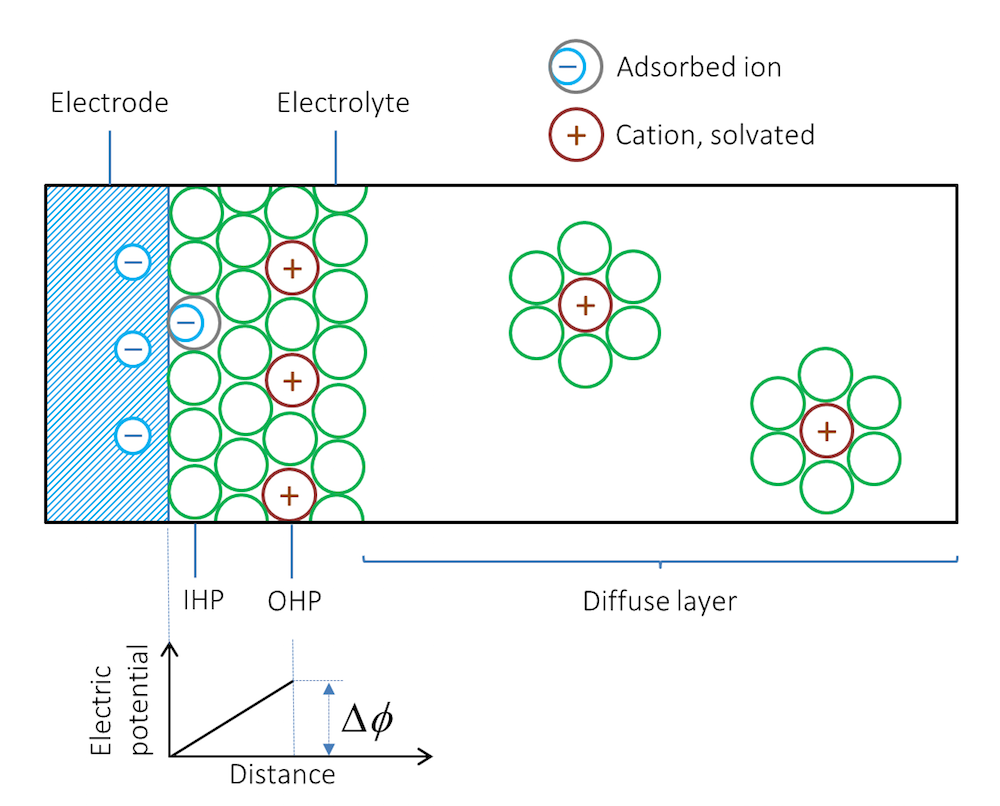
图 2. 双电层示意图。绿色圆圈表示溶剂分子,双电层右侧实际上充满了溶剂分子,但图中仅绘制了溶剂化离子周围的溶剂分子。
金属表面和离子层形成了双电层。在描述双电层的电势差 ΔΦ 时,没有施加任何净电流。
不同金属对电子的吸附能力不同,因此吸引带不同电荷数离子的能力也不同。这意味着在没有电流通过的情况下,相同电解质中不同金属的双电层电势是不同的。
如果将两个由不同金属制成的金属条浸入同一电解质中,并使用高阻抗电压表来测量电势,以避免任何电流流动,就能测量出两个金属条(电极)之间的电势差。图 3展示了金属条、带电双电层和电解质的电势分布示意图,其中高阻抗电压表用一个圆圈表示。
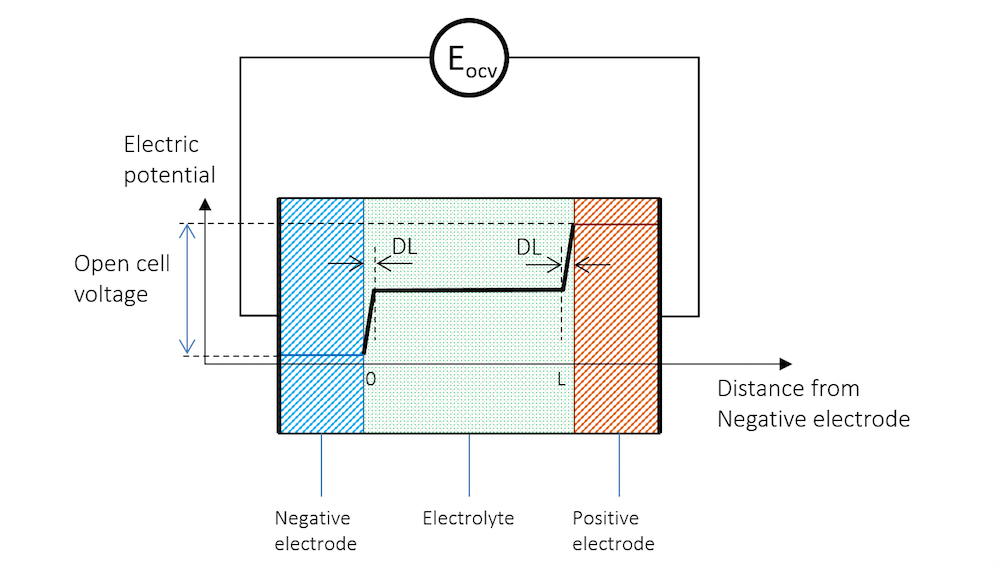
图 3. 负极、电解质和正极的电势分布情况,正极与高阻抗电压表连接以测量开路电压。
现在,这两个金属条构成了这个小型电池的电极,其中惰性较高的金属(还原电势较高)获得正电势,惰性较低的金属(还原电势较低)获得负电势。
在图 3 中,两个电极之间的电势差是保持系统电流流动所需的精确临界值。当电池处于断路(无净电流)且平衡状态时,电池电压被称为开路电压(OCV),在图 3中用EOCV 表示。
由惰性较低的锌和惰性较高的铜金属条制成的电池便符合上述情况。这时,发生在阳极的反应为锌溶解,发生在阴极的反应为质子还原生成氢。如此案例模型所述,将这两个金属条插进一只橙子,就可以制成一个简易电池,其中橙汁为电解质。
需要注意的是,几乎是不可能测量电极的平衡电势,因为只要将测量电极插入到电解质中来测量另一个电极的电势,测量电极周围就会产生带电双电层。所以,电极电势始终通过与高阻抗电压表相连的参比电极对照来测量。高阻抗确保了测量电极不会受到任何会改变电极电势的电流的影响。
参比电极的位置如图 4所示。当静电流为零时,对照参比电极测得的电极电势通常被称为平衡电势,在图 4中用 Ee,vs Ref表示。请注意,图 4 中的参比电极和高阻抗电压表用于测量负极的平衡电势。
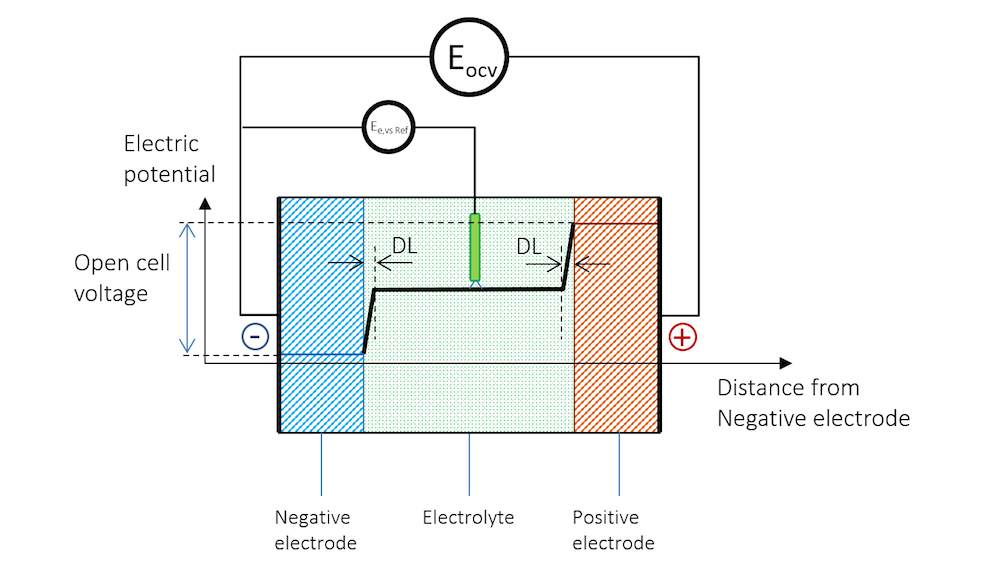
图 4. 浸在电解质中的参比电极表面也形成了双电层,因此对电极电势的测量产生影响。
放电过程中的电势
现在,我们可以通过外部电路中的载荷将两个金属条电极连接在一起,详见图 5。这里我们假设集流体和馈电器能够完美地使电流均匀、垂直地分布在电极上,因此电势在电极的垂直方向上也是均匀的,仅沿电池厚度方向(以负极为起点)发生变化。
将两端电极连接载荷后,负极的电势随之增加,双电层的电势差进而减小。较高的电势会强行将金属阳离子排到电解质中,并在阳极反应中将电子释放到外部电路。此小型电池的阳极反应可以表示为:
正极的电势较低,吸引了更多带正电的离子,这些离子能够接收阴极反应中排出的电子。同时,在这种情况下,双电层中的总电势差减小。在这个小型电池中,惰性较高的金属上的阴极反应可能是析氢,其第一步可能涉及形成吸附的氢原子:
图 5 清晰地解释了开路电压和放电过程的电势变化,以及为什么放电过程中电池电压会降低。
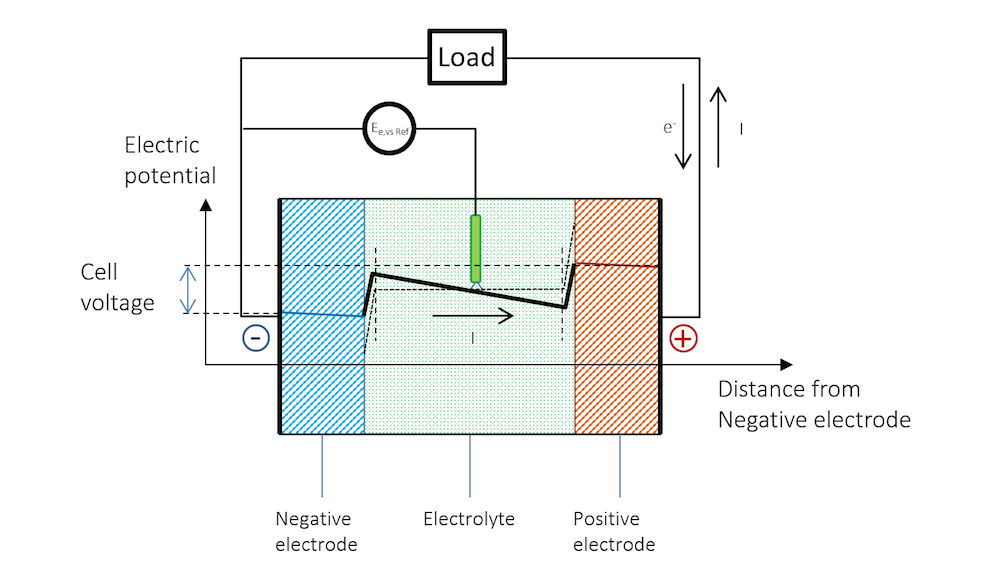
图 5. 放电过程中的电池电势变化。请注意,由于欧姆降,金属条(蓝色和红色区域)的电势存在斜率。请注意,在金属中,电流由电子传导,但根据定义,电流方向与电子流动方向相反。在其他材料中,电荷载体可以是负电荷或正电荷。按照惯例,无论材料和传导机理如何,电流总是假定为正电荷流动的方向。
在放电过程中,由于参比电极中无电流通过,参比电极的电势相对于溶液保持不变,即参比电极不会被极化。因此,参比电极可分别测量两个金属条电极的极化。在测量时,我们将同时获得沿金属条厚度上的欧姆损耗。这些损耗可以通过蓝色和红色区域的缓慢斜率看出,如果将参比电极置于中间,那么电解质中一半欧姆损耗也可以被看到。
图 5 表明, 金属和双电层外电解质中的电流遵循欧姆定律,尽管在很多电池电解质中,扩散作用也可能起到一定作用。在双电层外的电解质区域,电流确实从正电势流向负电势。
模拟电池和其他电化学电池时,双电层的电势分布精度达到了纳米级,而电极和电解质的厚度通常为毫米级。因此,在数值模拟中,双电层被视为不连续体。我们用一个因变量来描述电解质的电势,通常表示为Φl;用另一个因变量描述金属电极的电势,通常表示用为Φs。由此,双电层上的电势差定义为 ΔΦ = Φs – Φl。
电荷转移反应,电荷转移电流和过电位
双电层上无电流通过时和有电流通过时的电势差被称为过电位。与之前一样,我们只能对照参比电极来测量带电双电层,因此测量过电位 η 时,也需要对照参比电极。
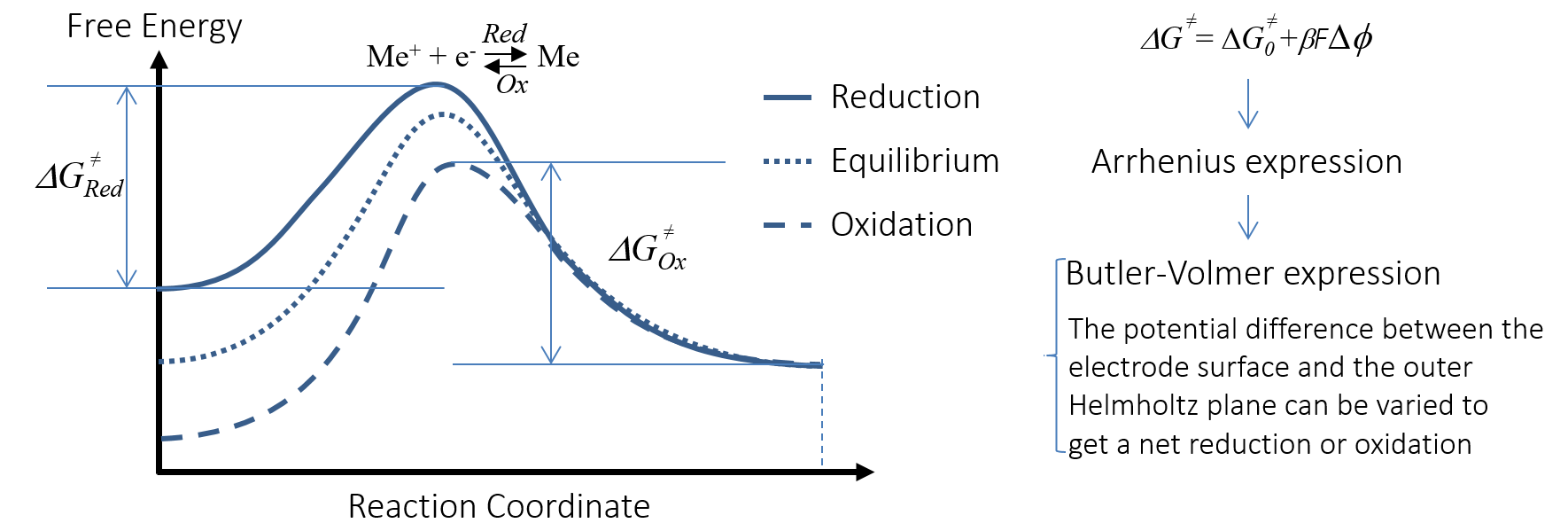
过电位能够改变电荷转移反应(即阳极氧化反应和阴极还原反应)的活化能。图 6 以金属 Me 被阳极氧化为 Me+ 为例,直观地展示了这一过程。在活化能图中,x 轴为负极氧化还原反应的反应坐标。该图描述了自由能和双电层电势差 Φ之间的关系。
图 6. 电荷转移反应的活化能随双电层电势差的变化,这一过程加快或减慢了电荷转移反应。
通过增加负极的电势,可以加快阳极氧化反应的速率,从而略微减小双电层的(负)电势差。在上图中,电势改变了带电物质的自由能。因此,电荷转移反应从充当阳极的金属条中“夺取”了电子,并将金属离子释放到电解质中。电子通过外部电路流经载荷到达正极,如图 5所示。图 5还显示了电解质中的离子在电场中迁移,同时将电解质中的电流输送到正极。
图 5 和图 6 中的反应过程也可以用电荷转移电流密度 ict 与电势的函数关系表示,如图 7 所示。两条曲线显示了电解质和金属界面上的电荷转移电流密度随电势的变化。蓝色和红色曲线分别表示负极和正极。
在放电过程中,当阳极过电位为 ηa 时,负极的阳极电流密度值为 ict,a,即电极被正极化,这也图 5 的描述一致。电势差 ΔΦ 是一个较小的负值,而在平衡状态下,电势差变为一个较大的负值,从而产生正电位。顾名思义,阳极电流即为正电流。
正极被负极化,根据其定义,即正极释放出带负电的阴极电流。在这种情况下,如果金属条的面积相等(基尔霍夫数),那么电流的值 ict,c 与阳极电流密度的绝对值相等,但符号相反。对应的阴极过电位为 ηc。如果不存在质量传输限制,那么 Butler-Volmer 方程可以描述图 7 中的红色和蓝色曲线。
与图 5 一样,图 7 还解释了为什么与图 3 中的开路电压相比,放电过程中的电池电压 Ecell 降低了。实际上,电池电压的降幅可能比图 7 中显示的更大,这是因为一部分电势也在欧姆损耗中损失了,只不过图中未包含。
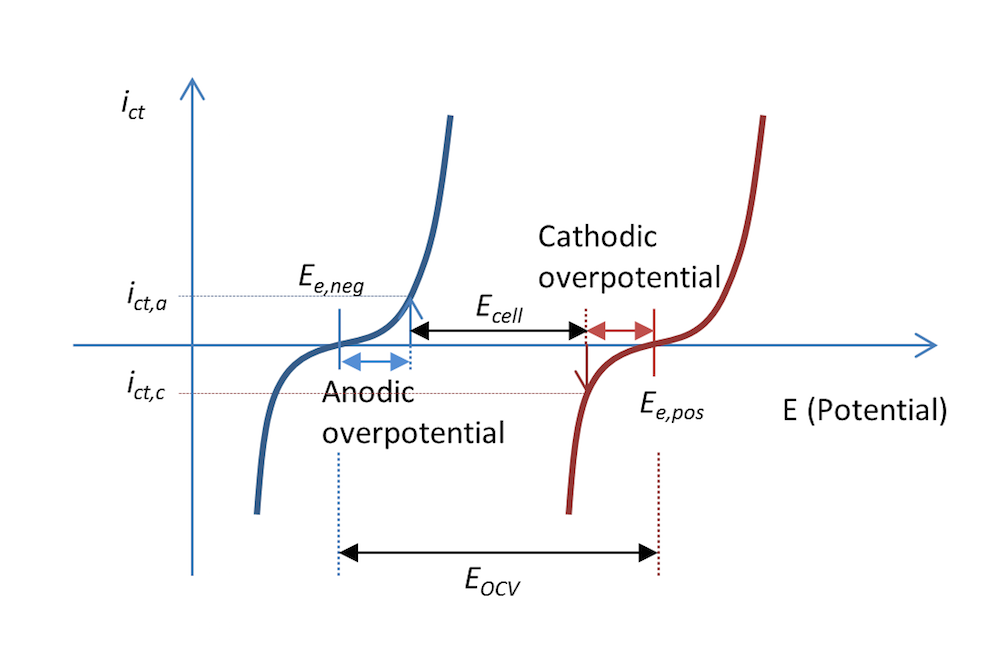
图 7. 在放电过程中,电荷转移电流密度与金属条电池中的负极电势和正极电势的函数关系。在这个示例中,放电过程中的电流密度为 abs(ict,c) = ict,a。
为电池充电
假设现在要为金属条电池充电。在充电过程,电荷转移反应须逆向进行,这样才能使负极发生阴极电荷转移反应,正极发生阳极电荷转移反应。
图 8显示,为了实现再充电,负极必须增强自身的活性,这将使带电双电层的电势升高。这一过程与与图 6 中的净还原反应相对应。负极现在变成了带负电荷转移电流密度的阴极。阴极还原反应如下:
正极必须增强自身的活性,这也会使带电双电层的电势升高。这一过程对应的是电池的净氧化反应。正极现在变成了带正电荷转移电流密度的阳极。在含水电解质中,惰性较高的金属条中通常发生的是氢氧离子的氧化反应。氧化反应的第一步可能涉及氢氧基的吸附:
第二步将生成水和氧气。为了将金属离子释放到溶液中,金属的还原电势越高,所需的电势也就越高。通常情况下,水电解质中的反应首先是氧化氢氧离子,或者分解水并产生氧气。
图 8 解释了为什么电池充电所需的电压比开路电压更高。
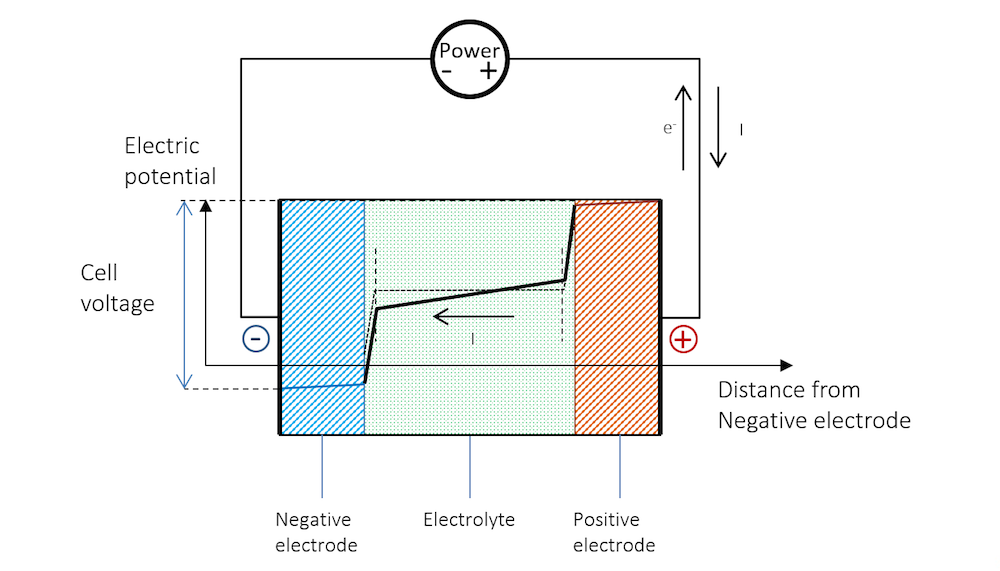
图 8. 充电过程中电池的电势。请注意,充电过程与放电过程一样,由于电阻降,两个金属条(蓝线和红线区域)的电势存在斜率。
图 9 显示了由发生在两个金属电极表面的电荷转移反应引起的电流密度。负极被正极化,释放出阴极电流,根据其定义,阴极电流带负电。正极的活性增强;即正极极化,获得阳极电流。下图也解释了为什么在充电过程中,电池电压必须高于开路电池电压,才能驱动所需的阳极和阴极电流。
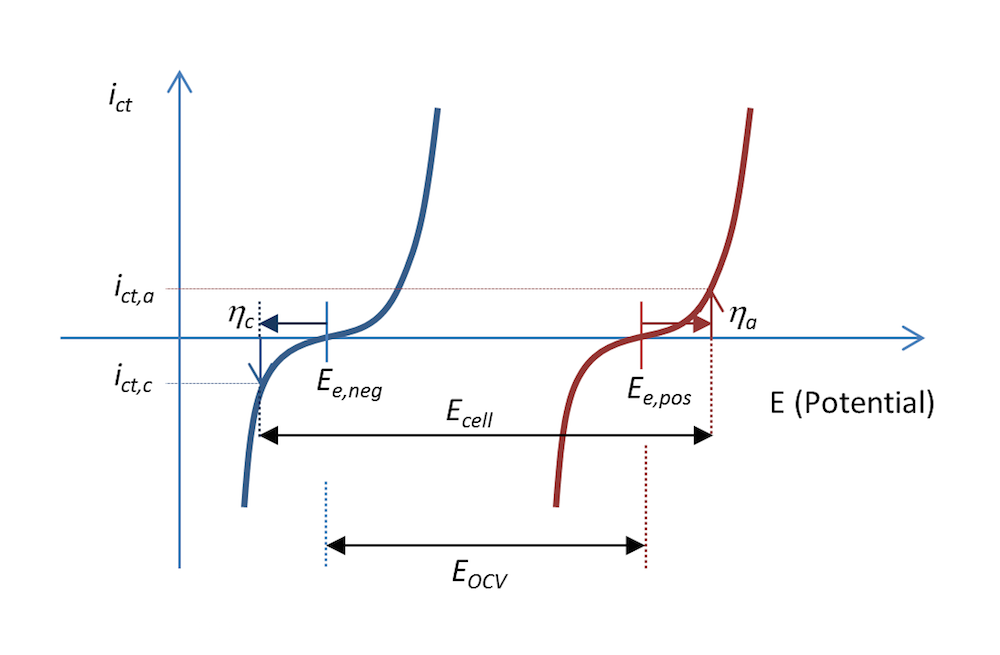
图 9. 在充电过程中,当电流密度为 ict 时,电荷转移电流密度与金属条电池中负极电势和正极电势的函数关系。
多孔电极
在现实中,大多数电池使用的是多孔电极,而不是将固体金属条作为电极。这样做可以为电化学反应提供更大的表面积,从而使电池单元的电能输出不变,而质量更轻、体积更加小巧。在这些电池中,电极的小孔中含有电解质,称为孔隙电解质。孔壁与孔隙电解质接触时,会在其周围形成许多带电双电层,这不仅增加了表面积,还减少了局部电荷转移电流密度以及放电和再充电过程中的过电位损失。
图 10 显示了带多孔电极的电池在开路电压下的电势分布。对自由电解质和孔隙电解质中的电解质电势均进行了定义。
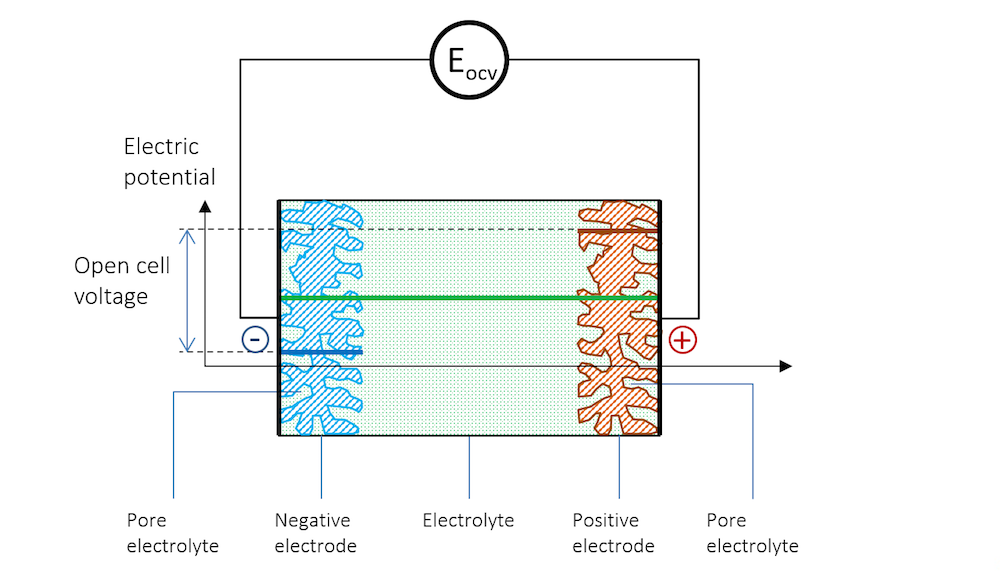
图 10. 带多孔电极的电池内,电解质、孔隙电解质和多孔金属中的电势分布。
当电池放电时,电流从负极的电极材料流向孔隙电解质。即在两个电极之间,电流从负极多孔电极的馈电器流向电解质的边缘,沿 x轴方向从左向右,孔隙电解质中的纯欧姆电流密度逐渐增加,如图 11 所示。
由于平均电流密度在 x 方向上的分布不均匀,因此孔隙电解质中电势分布同样不是斜率不变的曲线。电势分布曲线如图 11所示。在负极的孔隙电解质中,电解质电势(绿色曲线)的斜率随x的增加而增大。多孔金属的电势斜率(蓝色曲线)随x的增加而减小,这是因为在电荷转移反应中电流沿x轴转移到了电解质中。
在正极中,化学反应逆向进行。在面向自由电解质的边缘处,孔隙电解质的电势(绿色)达到最大,之后随 x 的增加而减小,这是因为电流从正极的孔隙电解质转移到了多孔金属中。随着越来越多的电流从孔电解质中传输出来,多孔金属(红色区域)中的电势斜率随 x 的增加而增大。在集流体处,所有电流流入金属。
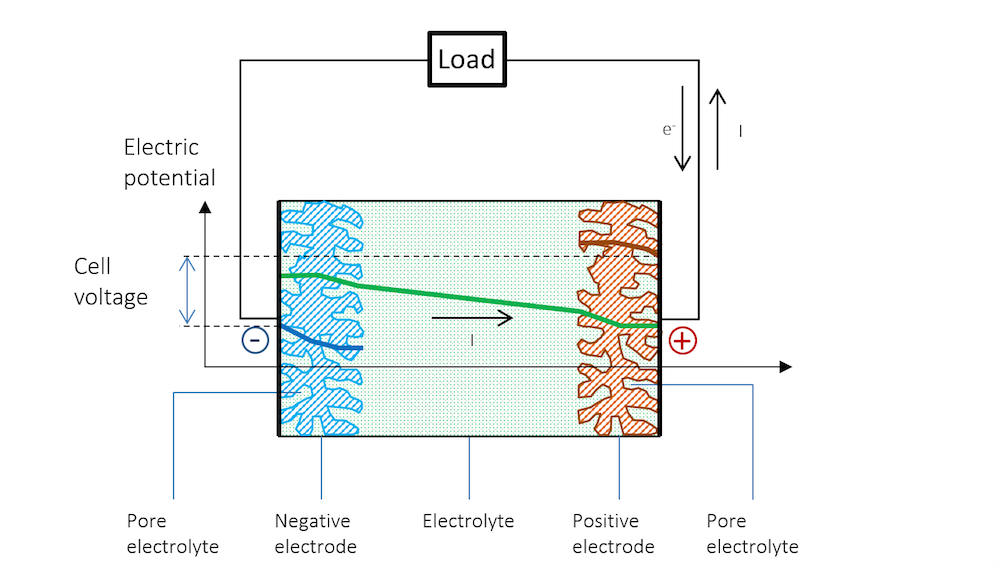
图 11.多孔电极电池放电过程中的电势分布。
总结
虽然本篇博客讨论的主题并不是研究热点,但是理解上述原理可以帮助您清楚地理解电化学概念。不仅如此,您还需要阅读一些专业资料,并且亲自动手进行建模和仿真。
扩展阅读
- 橙子电池模型
- 一维等温锂离子电池模型
- J. O’M. Bockris and A. K. N. Reddy, Modern Electrochemistry Volume 2, Springer-Verlag, 1970.
- J. Newman and K. E. Thomas-Alyea, Electrochemical Systems 3rd Edition, Wiley, 2004.



评论 (9)
一泽 刘
2021-06-09请问最后的多孔电极电势分布考虑了双电层的影响了吗
Ed Fontes
2021-06-09 COMSOL 员工Dear Izawa Liu,
Yes it does. This is included in the expression for the electrode kinetics (figure 9). The overpotential is the difference in potential over the charged double layer at equilibrium and when there is a net charge transfer. The two potentials used are the local electronic potential and the local ionic potential at the reacting site. In porous electrode theory, the difference between these two potential is the potential difference over the charged double layer.
Best regards,
Ed
xl 李
2022-06-14工程师您好,您讲的很通透,受益匪浅,还有个问题想问您:图三中的双电层结构有没有可能出现“\_____/”的电势分布图(其中左侧的电势要低些,右侧要高些)
yongchao wang
2022-06-30 COMSOL 员工当两个相同或性质相近的表面均吸附负离子(即外亥姆霍兹平面由负离子组成),此时可以在溶液中形成“\_____/”的电势分布,但是并不会形成原电池,因为从电化学角度分析,两个电极的电化学反应由阴阳极反应组成,不同的反应其电位不同,其产生或消耗的离子不同,最终导致双电层的结构正好相反。
xnmao
2023-04-01您好,我有一个基础的概念没理解。
在#电池内的双电层结构#中提到,*负离子是被接触吸附到带负电的表面上。由溶剂分子和被接触吸附的离子组成的物质层被表示为内亥姆霍兹平面*。
这是基于什么原理呢?我从静电相互作用的角度去理解,负离子和负电荷的表面为什么没有相互排斥呢?
Yi Li
2023-07-25 COMSOL 员工在界面处会有吸附现象发生,如果吸附力大于静电力,那么即使同种电荷也可以稳定处于界面处。
淑静 张
2023-09-07你好,图3模型中,在铜锌电池处于平衡状态时,若改变电解质中阳离子浓度(如调整Zn2+浓度),会影响负极侧的双电层电位和电极电势吗?如果有影响,会是线性还是非线性呢?
Ed Fontes
2023-09-07 COMSOL 员工Dear Shujing,
It will have an impact on the negative electrode in the case of Zn. The electrode potential (which is “caused” by the double layer) depends nonlinearly on the zink-ion concentration (or activity). This is described by the Nernst equation. For example, if the electrode reaction is Zn = Zn2+ + 2e-, you get E = E0 + (RT/2F)ln(Czn2+) where E0 is a reference potential. This means that the driving force for the anodic reaction at the negative electrode during discharge decreases with increasing Zn2+ concentration. The electrode potential becomes more positive when you really want it to be as negative as possible, to get more cell voltage.
Best Regards,
Ed
Yi Fan Wang
2023-09-07 COMSOL 员工您好,双电层包括紧密层和分散层,所以说电解质的改变会引起分散层的改变,是非线性的改变。标准电极电势可以根据能斯特方程计算,能斯特方程中包含了氧化态与还原态的比值。