在上一篇博客文章 理论介绍——什么是规范固定?中,我们介绍了规范固定的理论知识。也就是说,为什么以及什么时候需要它。在这里,我们继续讨论如何实现规范固定以及如何在 COMSOL Multiphysics® 软件中使用规范固定。
固定规范的使用:通常没有必要
在 之前的博客文章中,我们介绍了 AC/DC 模块物理接口中的一些势场。即电势 V,磁标势 V_m 和磁矢势 \textbf{A}。
我们已经知道,除非已经定义 V 和 V_m 的参考值并且已被指定,则势场 \nabla\cdot\textbf{A}
不是唯一确定的。当解不是唯一时,要计算的数值问题会出现奇异。在这种情况下,COMSOL Multiphysics 默认使用迭代求解器,该迭代求解器将会得到收敛解。求解中的这些变量是相互等效的,对应相同的物理场(\textbf{E},\textbf{D},\textbf{H},或 \textbf{B}—根据环境)。
查看 知识库,以了解迭代求解器和直接求解器之间的区别。
在 AC/DC 模块(COMSOL Multiphysics 的一个附加产品)中,有三个可求解矢量 \textbf{A} 的物理接口:
- 磁场(mf),它基于公式 \textbf{A}。,其中 \textbf{A} 是唯一的因变量。在稳态场中,如果不使用规范进行固定,则该解并不是唯一的;而在非稳态场中,由于感应区域的附加项具有数值意义,因此满足求解唯一性。
- 磁场和电场(mef),求解完全耦合的 \textbf{A} 场和 V 场。由于 规范变换,除非 \nabla\cdot\textbf{A}
指定,否则没有唯一解。 - 旋转机械,磁(rmm),公式 \textbf{A} 和 公式 V_m 的组合。公式 \textbf{A} 用于描述导电(存在电流)域,而公式 V_m 用于气隙和其他非导电域。这两个公式在它们共同的连接边界上耦合。由于 rmm 接口是混合公式,因此适用磁场(mf)接口的规范固定特征。
综上,对于无需规范固定的求解类型,下表列出了 mf,mef 和 rmm 接口对应的求解属性和所需的求解器。由于这三个接口具有默认的迭代求解器,因此通常不需要规范固定。
| 接口,属性 | 稳态 | 瞬态, \sigma=0 | 瞬态, \sigma>0 | 频域, \omega>0 |
|---|---|---|---|---|
| mf, rmm 解 |
非唯一 | 非唯一 | 唯一 | 唯一 |
| mf,rmm
求解器 |
仅迭代 | 仅迭代 | 迭代或直接 | 迭代或直接 |
| mef 解 |
非唯一 | 需要mf接口代替 | 需要mf接口代替 | 非唯一 |
| mef 求解器 |
仅迭代 | 需要mf接口代替 | 需要mf接口代替 | 仅迭代 |
值得一提的是,即使在势场缺乏唯一解时,物理场 \textbf{E} 和 \textbf{B} 始终是唯一的。势场不能直接测量,也没有直接的物理意义,因此对于势场而言,任何满足方程式的解都可以。
作为说明,请使用案例库提供的 功率电感器的电感模型。该模型使用 mef 接口构建,并在频域中求解。模型中最初没有使用规范固定,后面使用了规范固定。
如下图所示,电势 V 存在显著差异,而电场 \textbf{E} 的数值保持不变。右上方的绘图显示了电势 V 在应用规范固定时在求解域上存在平滑过渡。相对与没有使用规范,如左上图所示,电势分布存在明显不同。有趣的是,我们称此规范(\nabla \cdot \textbf{A} = 0)为“库仑规范”,因为它强制约束电势 V 类似于 库仑电势,这是由静电荷密度引起的。由于物理场 \textbf{E} 和 \textbf{B} 相同,因此计算出的电抗值也一致。
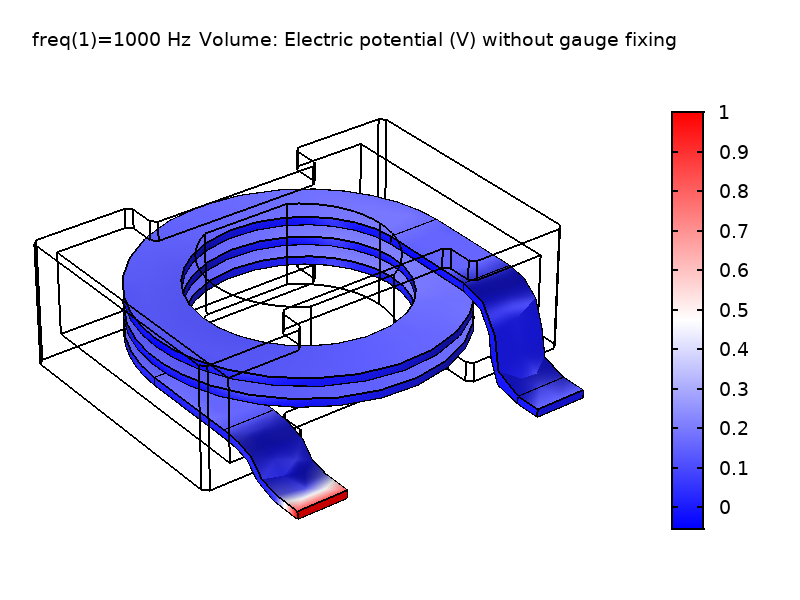
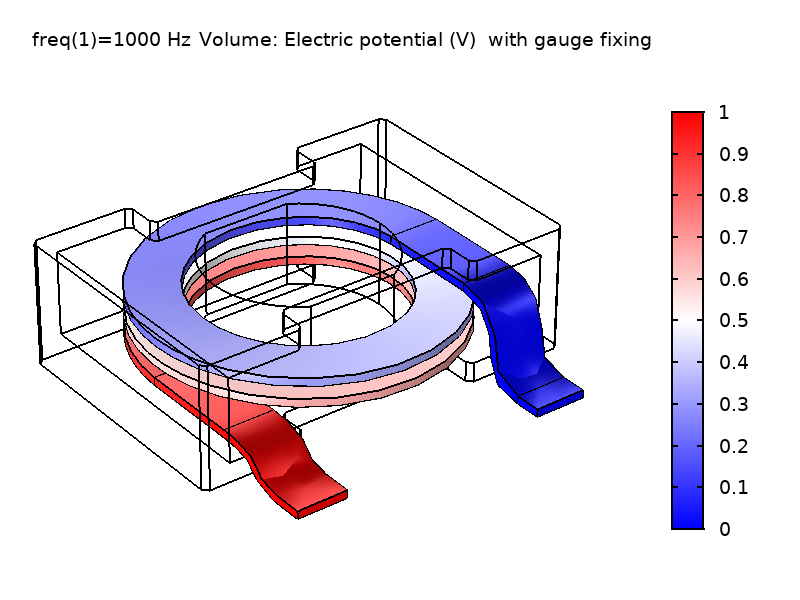
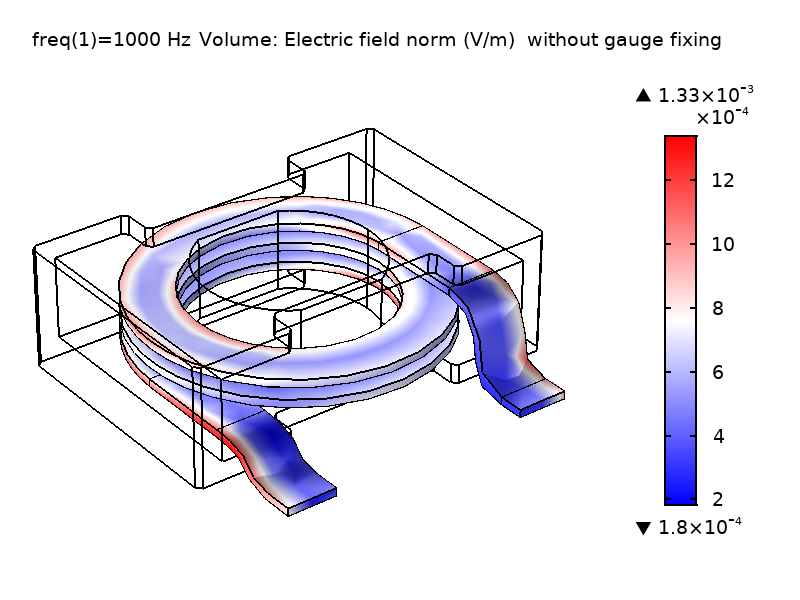
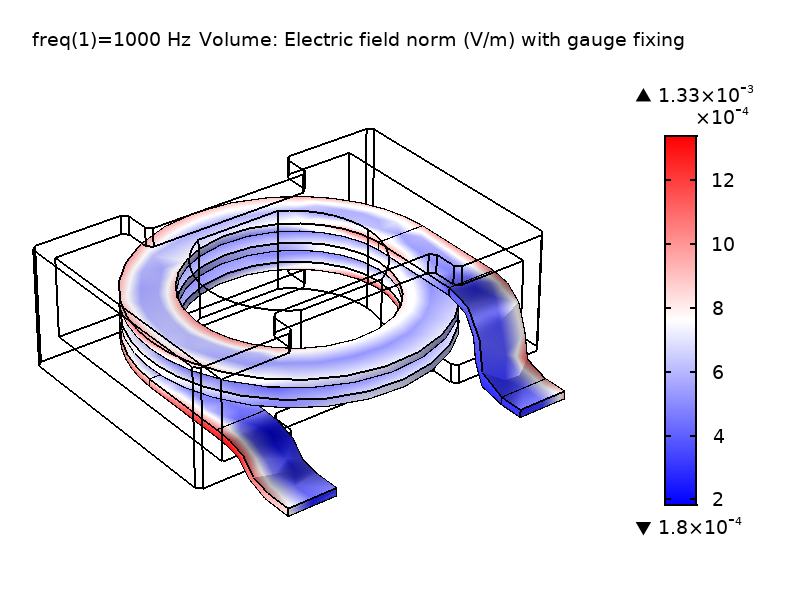
图1 未使用规范固定(左)和使用规范固定(右)情况下,求解的线圈域中的 \textbf{E}场和 V 场计算值的比较。
AC/DC 模块中的规范固定
当场 \textbf{A} 的解不是唯一的,并且当您想使用直接求解器时,通常需要进行规范固定。在涉及多物理场耦合的情况下,使用直接求解器可能是必需的或有益的,因为迭代求解器和预处理器通常仅对一种特定类型的物理场进行调整。同样,在求解 2D 模型时,默认使用直接求解器。
在 mf , mef 和 rmm 接口中,有一个域条件称为磁矢势规范固定。除了在 2D 和 2D 轴对称中求解平面外磁矢势时,该功能均可使用。假定矢量势在平面外方向恒定,则可以轻松实现库仑规范\nabla\cdot\textbf{A} = 0。
磁矢势规范固定功能引入了拉格朗日乘数 \psi 来满足库仑规范,从而产生两个耦合方程。以静磁学为例,第一个方程(稳态安培定律)适用于 \textbf{A} ,其表达示为
(1)
其中 \textbf{J}_e 是外部施加的电流密度.
第二个方程适用于 \psi,可以用库仑规范表示
(2)
在等式 1,变量\psi的作用类似于不可压缩流 Navier-Stokes 方程中的压力,其中压力增加了无散度流场的约束。
如 等式 1 所示,\psi 的量级大小没有特别的意义;只有它的梯度才在方程中起作用(它的作用就像电势一样)。通过提供一个让 \psi 影响 \textbf{A} 的机制,等式1 中 “类电流项” \nabla\psi 可以让方程组闭合。为了确保非奇异模型,有必要至少在一个点上约束 \psi 的数值。默认情况下,通过在界面设置中输入散度条件变量缩放 \psi_0 的数值(默认值 1 A/m),来约束 \psi 在磁绝缘边界上的数值。下图为使用不同 \psi_0 值的功率电感器模型的势场 \psi 和电场强度 \textbf{E}。可以看出,\psi 的量级变化对场 \textbf{E} 无影响。
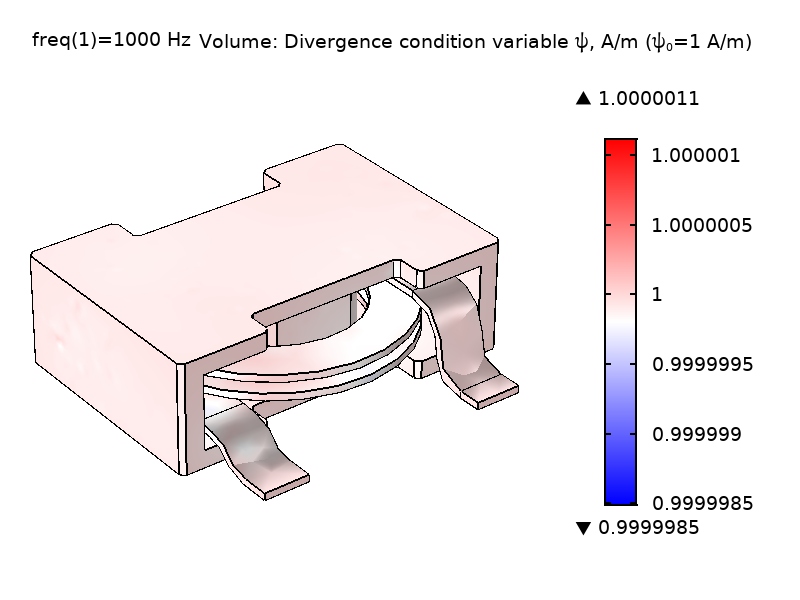
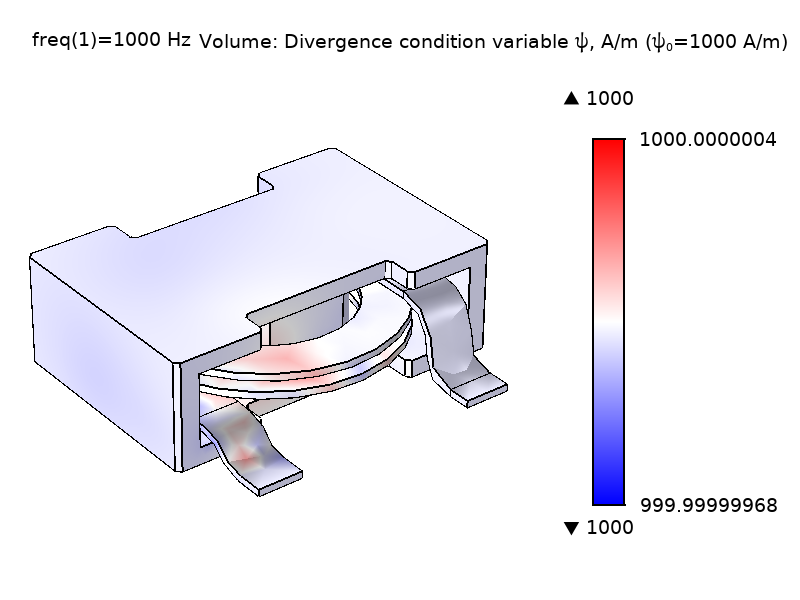
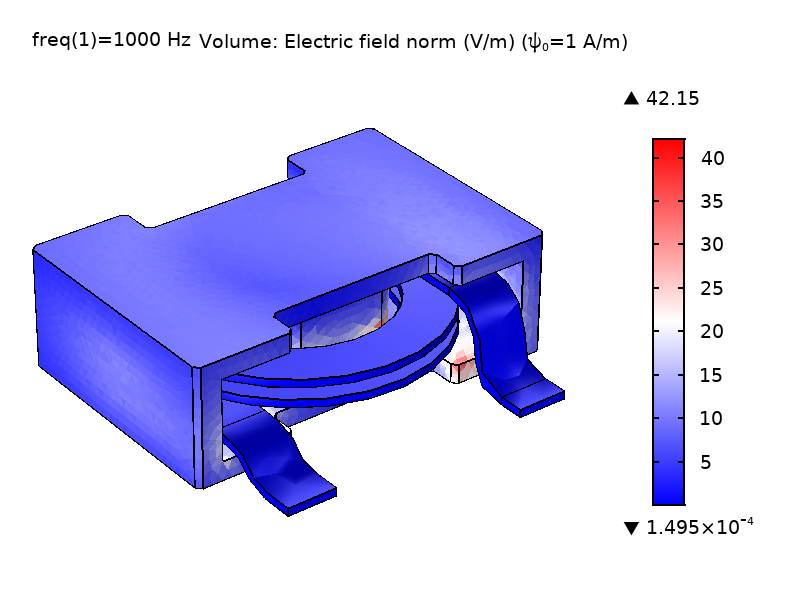
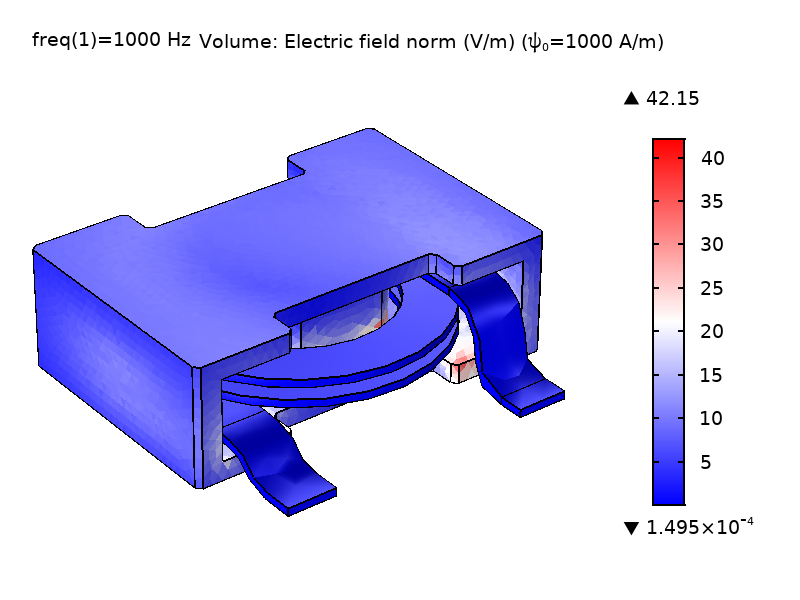
图2 使用不同的缩放比例 \psi 求解线圈和铁心域中的势场 \psi 和电场强度 \textbf{E} 的计算值比较。\psi_0 = 1 A/m (左) 和 \psi_0=1000 A/m (右)。
除非必须,否则不要使用规范固定,因为它会增加求解的变量数,这需要更多的内存和更多的时间来求解。根据不同的模型,如果使用规范固定,则计算时间可能会增加 30%–60%。值得一提的是,规范固定将导致系统矩阵的对角线为零。当使用直接求解器时,后者不是问题。但是迭代求解器必须在预处理器中使用更费时的方法(例如 Vanka 算法)。有关求解器的详细信息,请参考《COMSOL Reference Manual 》。默认情况下,求解器通常会考虑上述情况,因此通常不必担心系统矩阵结构的变化。
增强电流转换:规范固定的另一个作用
在安培定律中,默认满足电流守恒,这意味着施加的源电流密度和感应电流密度之和必须是螺旋结构的。在求解麦克斯韦方程时,这具有重要的意义。对于 mf 接口中的静态情况,被求解的方程表示为
(3)
对 等式 3左右两边取散度,可以得到
(4)
请注意,对于任意 \nabla\cdot(\nabla\times\textbf{F})=0 ,均满足 \textbf{F},等式 4 的左侧恒为零。因此,等式右侧,即外部源电流密度的散度也应为零,该方程式将完全无解。这使得 等式1 中引入的变量 \psi 有两个使用目的。除了执行 等式2 外,它还强制执行条件 \nabla\cdot(\textbf{J}+\nabla \psi)=0,这是 等式1 中固有的。换句话说,等式1 中的增加项 \nabla\psi 将抵消外部电流密度的任何差异,使修改后的方程右侧满足电流守恒。因此,如果将规范固定与外部电流密度结合在一起,它们在分析意义上不满足散度自由,则会产生意想不到的解。然后,规范固定将会在 \nabla\psi 中引入非物理的,很大的补偿电流密度,该模型将产生意外解。这可能会导致错误解,为便于观测该情况,建议在使用规范固定求解后可视化查看 \psi 场。如图2 第一行所示,在应用规范固定的区域,场 \psi 的大小只发生极小的变化。如果不是这样,指定的源电流密度很可能不满足安培定律的螺旋条件要求。在这里,应该适当添加以下内容:磁场(mf)接口的稳态计算默认为迭代求解器,对应用的源电流可以有类似的校正,因此对于物理场 \textbf{B},是否应用规范固定得到的结果不会有所不同。
对于 mf 接口(\sigma, \omega>0)中的动态情况,解是唯一的,无需添加约束条件 \nabla \cdot \textbf{A} = 0。mf 接口提供了一个切换选项,在规范固定设置中可从稳态(\nabla\cdot \textbf{A}=0)切换到研究控制。下面我们来讨论其具体含义。在与时间有关的研究中,mf 接口可求解下面的方程式:
(5)
\nabla \times \textbf
{A} )= \textbf{J}
它考虑了感应电流密度,但忽略了位移电流密度(可看作准静态近似)。在这种情况下,相对于稳态约束条件 \nabla\cdot\textbf{A}=0 ,规范固定在研究控制选项中,通过约束 \nabla \cdot (\sigma \textbf{A})=0 来满足电流守恒条件,这与 等式 5 的散度条件类似。同样,对于频域研究,可以包含感应和位移两种电流密度,对应“完整的麦克斯韦方程形式”,除了约束 \nabla \cdot \textbf{A}=0外,对于总电流密度 \textbf{J},研究控制下的规范固定还约束了 \nabla\cdot\textbf{J}= 0 。使用这种散度约束的主要好处是提高了数值稳定性,尤其是在接近稳态极限时。
动手尝试:使用规范固定
为了更好地理解规范固定,可以自己做一些实验。下表列出了“案例库”中的一些模型,您可以分别使用弃用和添加规范固定两种方式进行求解,然后比较结果和计算时间。例如,在 E 磁芯变压器模型 中,使用直接求解器通过规范固定来求解,并将电导率设置为零。您还可以使用相同的直接求解器求解,但不使用规范固定,同时设置线圈之外的所有区域电导率 \sigma=1 S/m。您会注意到,模型的求解时间仅为使用规范固定时的一半。
| 物理场接口 | 研究类型 | 案例下载库中的模型 |
|---|---|---|
| mf | 稳态 | 亥姆霍兹线圈中的磁场 |
| 瞬态 | E磁芯变压器 | |
| 频域 | 涡流 | |
| mef | 频域 | 功率电感器的电感 |
| rmm | 瞬态 | 永磁电机三维模型 |
结语
在本篇博客文章中,首先,我们指出除非选择直接求解器,否则在使用 AC/DC 模块进行电磁仿真时,不需要规范固定。然后,我们介绍了如何在三个相关的物理接口中实现和使用规范固定,并讨论了规范固定的优缺点。最后,我们列出了一些您可能感兴趣的案例模型列表。






评论 (0)