
阅读之前的一篇博客 “线性静态问题的网格剖分注意事项”,我们发现,有限元模型的解将能在网格细化的限度内收敛至真实解。不仅如此,我们还了解到,在误差较高的区域,可以通过自适应网格细化生成包含更小单元的网格,而不是简单地在整个模型内都使用较小的网格单元。在这篇博客中,我们将讨论有限元建模过程中一些常见的由模型奇异性造成的错误。
结构力学示例
让我们来分析在单轴应力作用下一个含方孔平板的受力情况。这与之前讲解过的一个示例较为类似,都是利用平板的对称性而只对其中的四分之一进行受力分析。
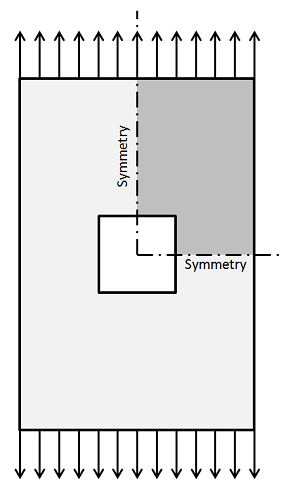
与之前一样,我们可以通过自适应网格细化让 COMSOL 在预计误差较大的区域内插入更多的单元:
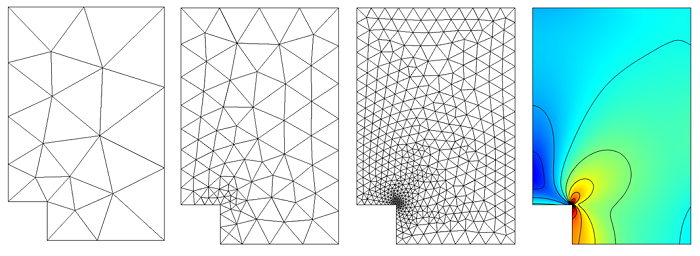
我们观察后发现,插入到锐孔内拐角的网格单元越来越小。让我们以网格尺寸函数的形式绘制出内拐角处的应力图:
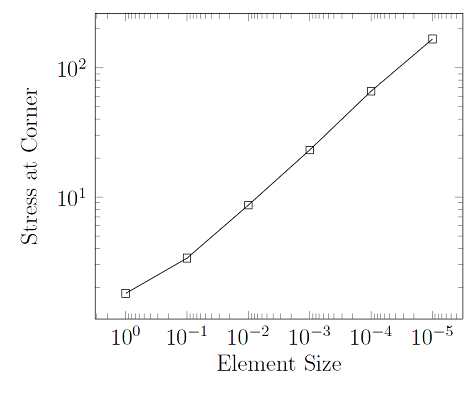
从上图中可以看出,不论网格细化到什么程度,应力值一直呈递增趋势。事实也是如此:因为模型中存在奇异性,所以尖角处的应力值不随网格细化程度而收敛。实际上这是完全准确的:尖角处的应力在理论上趋于无穷。每次您看到此类不收敛的行为表现时,就应当联想到模型中存在奇异性。
在实际的结构工程中,应极力避免产生尖锐的内角。当然您完全有理由说,可以把存在奇异性的尖角磨平来防止此类问题出现;这样,我们不难预测到模型中的应力将会随网格细化而收敛,但是在内角处仍需要插入大量的单元。所以接下来将介绍其他几种处理奇异性的方法。
将模型当作整体来研究
处理奇异性的一种方式就是忽略它们。有限元方法的一个重要特征就是它允许局部存在不准确,因为其出发点就是为了最小化模型中的整体误差。我们在上述模型中预估的应力值并不正确,但如果在离奇异性产生点约 2~3 个网格单元处求应力,那么结果将会收敛。因此,如果我们考虑远离奇异性产生处的应力将不会受奇异性影响。
对解求导
同样不可忽略的是,奇异性会对解的求导产生影响。在结构力学中,我们需求解位移场 \bf{u},进而从应变 \bf{\sigma =C : \epsilon} 推导应力,其中应变由位移场的变化率 \epsilon = 1/2 \bf{ [ (\nabla u)^T + \nabla u] } 定义。所以当把应力作为位移场的变化率来考虑时,就更清楚地解释了为什么在尖角处的应力趋向于无穷。然而,如果只考虑解 \bf{u},那么即便在尖角处也不会产生奇异性,结果将随网格细化而收敛。
在奇异性产生处求积分
另一个常见的允许奇异性存在的情况是,您仅对模型输出的积分值感兴趣。例如一个线性材料的总弹性势能可表示为:
如果在一个包含奇异性的域内对其求值,例如带有方孔的平板,那么积分会随网格细化迅速收敛,即便被积函数在域内任意一点不收敛。如果您希望得到模型内一个域(或边界)处的被积函数,那么您的模型中可以存在奇异性。无论是尖角还是圆角,积分值最终都会收敛至相同的值。这种情形常见于电磁学,此时设备的电感和电容分别被表示为域内电场和磁场的积分形式。
关于网格剖分和模型中奇异性的总结
总的来说有三类情形允许在模型中存在奇异性:
- 当您不需要奇异点处的解,而是在离奇异点一定距离处求解;
- 当您不需要在在奇异点处解求导;
- 当您在奇异点周围的域(范围)或边界内求积分值,包括对解的导数进行积分。
在上述几种情况中,您可以通过网格细化观察解的收敛。对于模型中其他不收敛的地方也应仔细观察,以保证您对结果的解读不会产生偏差。
最后,仍然有一些情况需要 精确求出奇异点附近的场,但是模型可能很大,我们无法为所有的边应用圆角。在这些情形下,我们可以使用 子模型法,或拆拆分模型法。在可能存在奇异性的大型模型中,这种方法会首先使用相对粗化的网格来找出解,然后将信息传递给包含更细化网格和更圆滑拐角的子模型。轮毂的子模型示例演示了该方法的使用。






评论 (0)