如何构建多体动力学模块中的齿轮几何

高还原度的齿轮几何模型，对于执行耦合了其他物理现象的多体动力学仿真而言帮助巨大。考虑到这一点，COMSOL 在“零件库”中提供了很多内置零件，帮助用户免去手动创建几何体的麻烦。有了这些高度参数化的齿轮零件，创建多种多样的平行轴线齿轮和行星齿轮系变得更加得心应手。请阅读本文了解到如何使用不同类型的内置零件创建一个“多体动力学模块”中高还原度的齿轮模型。

内置齿轮零件的优势

虽然从理论上讲，我们能够在仿真中通过精确模拟齿轮间的接触相互作用，对机械装置进行分析。然而，若将此方法应用于多体动力学分析，计算时间会相当长。一个更好的方法是引入数学公式来模拟齿轮之间的接触和相互作用。

借助相应的公式，我们能创建出高还原度的齿轮几何模型，为执行瞬态和频域研究提供精确的惯性属性。除此之外，“零件库”中的齿轮几何也可用于计算静态接触分析中齿轮的啮合刚度，并且适用于多物理场的耦合模拟。需要注意的是，虽然并未对齿轮的啮合刚度进行有限元分析，但是这种刚度仍然客观存在于成对的齿轮齿接触中。在多体动力学分析中加入真实齿轮几何的另一个好处是：在建立物理场或执行后处理时，可以展示出更好的视觉效果。

使用“零件库”创建斜齿轮副几何模型。

虽然可以手动建立几何体，但使用内置零件会让工作变得更加简单、高效。这些零件本质上是参数化的，这意味着只需简单地调整几何参数，就可以改变零件的形状，包括自由添加轴和圆角等多个特征。这些零件经历了大量检验，验证输入数据以及齿轮、轴和接触边界等选择的有效性，这些检验步骤确保了零件的性能更加接近物理实体。在“零件库”的帮助下，指定齿轮的位置和方向、使齿轮啮合与配对的齿轮对齐等操作变得非常简单。这些零件还包含鲁棒性几何操作，在创建复杂的齿轮几何形状时十分好用；此外，我们还可手动更改零件的几何操作。

“零件库”中齿轮零件分为三类：外部啮合齿轮，内部啮合齿轮与齿条。如您希望了解“零件库”中有关齿轮零件的更多信息，请阅读齿轮模拟系列的博客文章。

基于单个齿轮构建齿轮系

“零件库”中的齿轮基本上都是单个齿轮或齿条，但在真实的应用条件下，齿轮一般都是成对使用。为此，我们要用单个的齿轮零件来构建齿轮系。为了清晰地解释构建步骤，我们将使用以下二维直齿轮副作为示例。已知的物理量如下：

• 第一个齿轮的位置（x_1,y_1）
• 第一个齿轮的节圆半径（r_1）
• 第二个齿轮的节圆半径（r_2）
• 第二个齿轮的角位置（\theta）

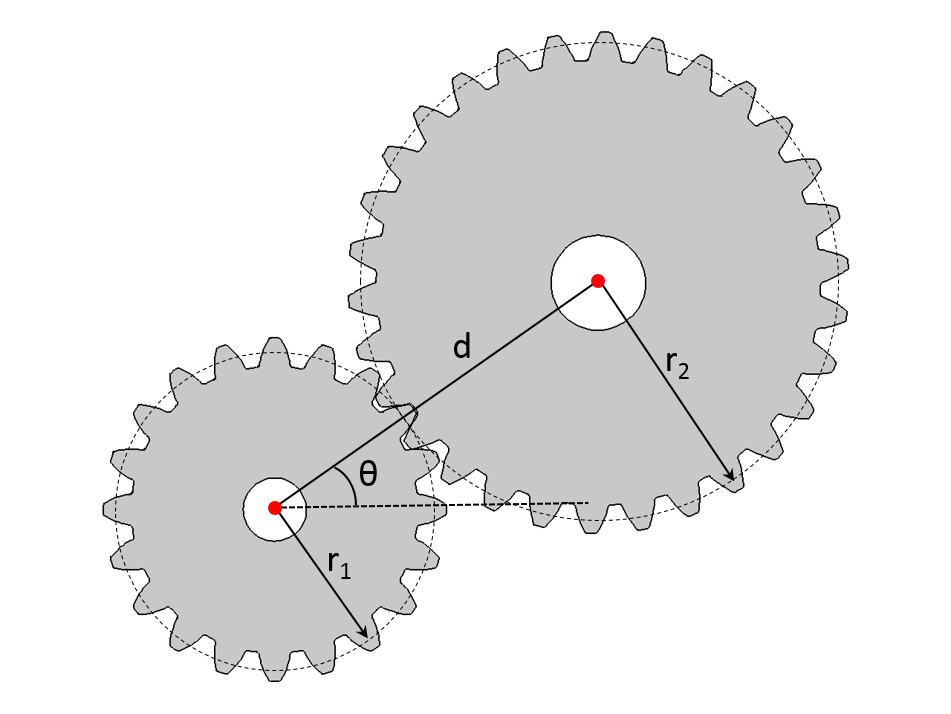
直齿轮副示意图，图中显示了两个齿轮的中心距和第二个齿轮的角位置。

为了将第二个齿轮设置在适当的位置，首先需要计算中心距 d：

将第二个齿轮的位置（x_2,y_2）定义为：

将第二个齿轮放置在正确的位置上后，下一步是对准两个齿轮的轮齿，在此示例中则称为啮合。具体方法是，将第二个齿轮在旋转中的啮合对齐角 \theta_a 定义为：

其中 \theta_{m1} 和 \theta_{m2} 分别表示两个齿轮的啮合周期，其表达式为：

其中 n_1 和 n_2 分别表示第一个和第二个齿轮的齿数。

计算完第二个齿轮的位置以及啮合对齐角后，我们将它们作为表达式或数字添加到第二个齿轮的输入参数栏中，如下图所示：

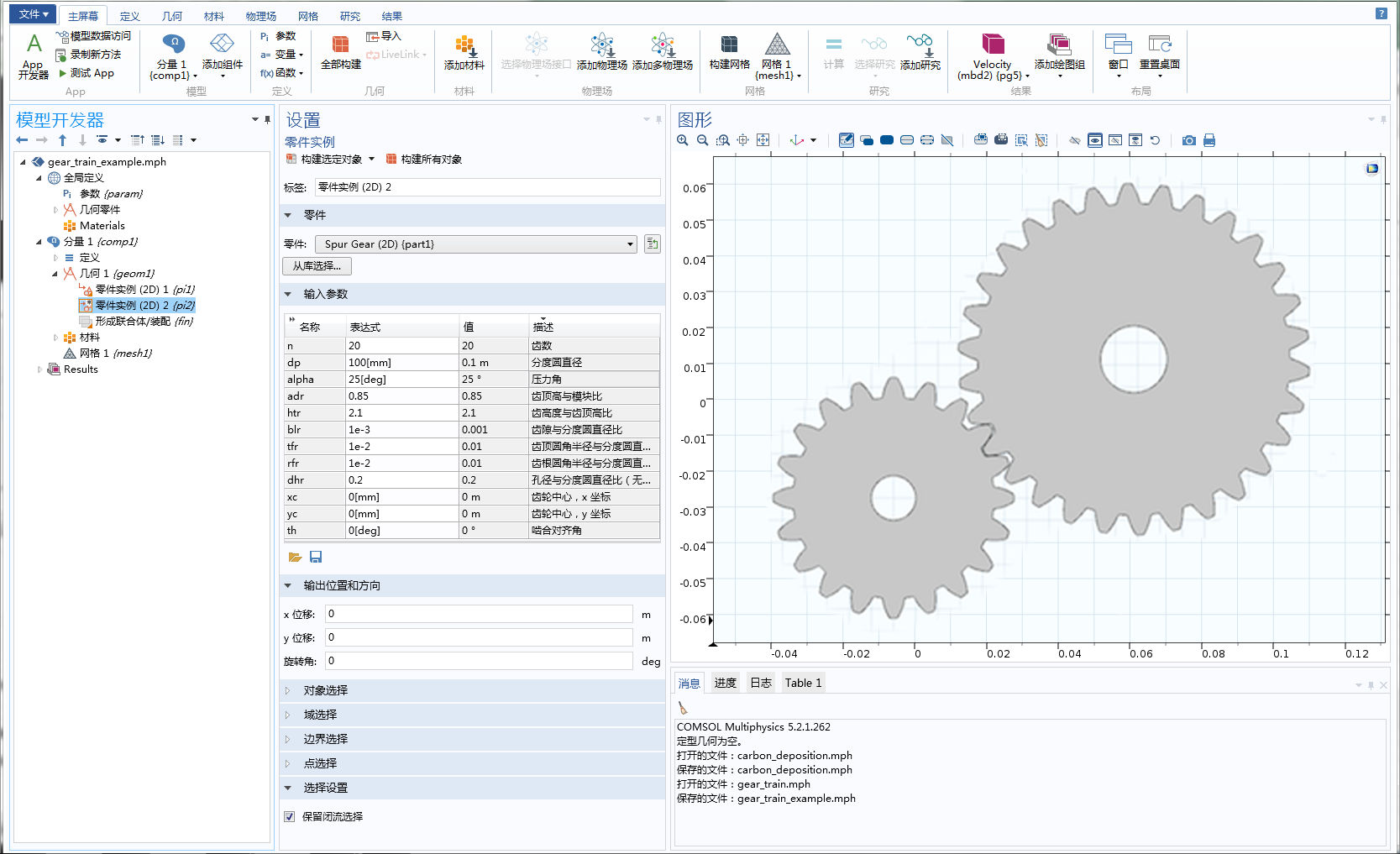
二维直齿轮零件的输入参数，红框内的参数为齿轮中心和啮合对齐角。

设立齿轮参数

在此示例中，我们使用渐开线曲线来定义齿廓。每一种齿轮应用都有其独特的齿形和尺寸，因此对于不同的应用，须选择相应类型的齿轮齿。以下输入参数可用于控制齿轮齿的形状和尺寸：

• 齿数（n）
• 分度圆直径（dp）
• 压力角（\alpha）
• 螺旋角（\beta）
• 齿顶高与模数比（adr）
• 齿高度与齿顶高比（htr）
• 齿隙与分度圆直径比（blr）
• 齿顶圆角半径与分度圆直径比（tfr）
• 齿根圆角半径与分度圆直径比（rfr）

若这些位置上不需要圆角，那么可以将齿顶圆角半径或齿根圆角半径设为零。

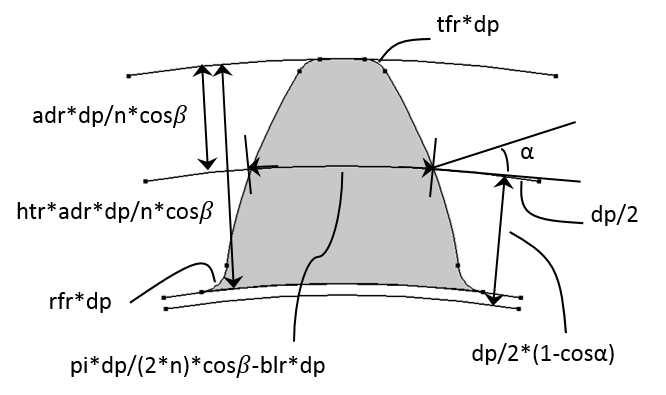
控制外部轮齿的各个输入参数。

大部分输入参数之间存在一定的物理关系，通过搭配使用这些参数能使几何结构具有更好的扩展性。我们可以利用这些输入参数计算出多个齿廓参数：

• 法向模数：m = dp/n*cos\beta
• 齿顶：ad = adr*m
• 齿高度：ht = htr*m
• 齿根高：dd = ht-ad
• 基圆直径：db = dp*\cos\alpha
• 齿顶圆角半径：tf = tfr*dp
• 齿根圆角半径：rf = rfr*dp
• 节圆处的齿厚度：t = \pi *m/2 -blr*dp

针对一些特殊的应用，须采用相应特定类型的齿轮齿。对于高速齿轮装置而言，高压角齿轮更为适合，因为其磨损率小于标准齿轮齿廓的磨损率。同时高速齿轮装置中还需专门留出齿隙，为轮齿之间的润滑油膜留出空间，防止齿轮过热和轮齿损坏；另一方面，在仪器、机床和机器人等精密设备中，应当避免出现齿隙，因为这些装置中的齿隙会导致输入轴和输出轴之间出现空转，从而难以实现准确的定位。

具有不同压力角和模数的齿轮。左图：具有标准齿廓的齿轮。中图：大压力角齿轮。右图：大模数齿轮。

齿轮毛坯和轴的几何模型

探讨完齿轮齿的细节后，我们来看一下影响齿轮形状和尺寸的其他参数。齿轮的几何结构可分解为三个零件：齿轮齿，齿轮毛坯和轴。齿轮轴的相关参数如下：

• 齿轮宽度与分度圆直径比（wgr）
• 环宽度与齿轮宽度比（wrr）
• 环外径与齿根直径比（dorr）
• 环内径与孔径比（dirr）

虽然轴并非齿轮的组成部分，但我们可以用内置齿轮零件在齿轮中心添加一个轴，齿轮的轴向位置可以与轴重叠。

• 轴长与分度圆直径比（lsr）
• 轴中心的相对轴向位置（zs）

在默认设置下，齿轮位于原点，其轴被设置为 z 轴，我们可以通过下列参数控制齿轮的位置和方向：

• 齿轮中心（\{xc, yc, zc\}）
• 齿轮轴（\{egx, egy, egz\}）

为了使齿轮啮合与啮合齿轮对齐，我们采用了啮合对齐角参数，以使齿轮围绕自己的轴线旋转。

• 啮合对齐角（th）

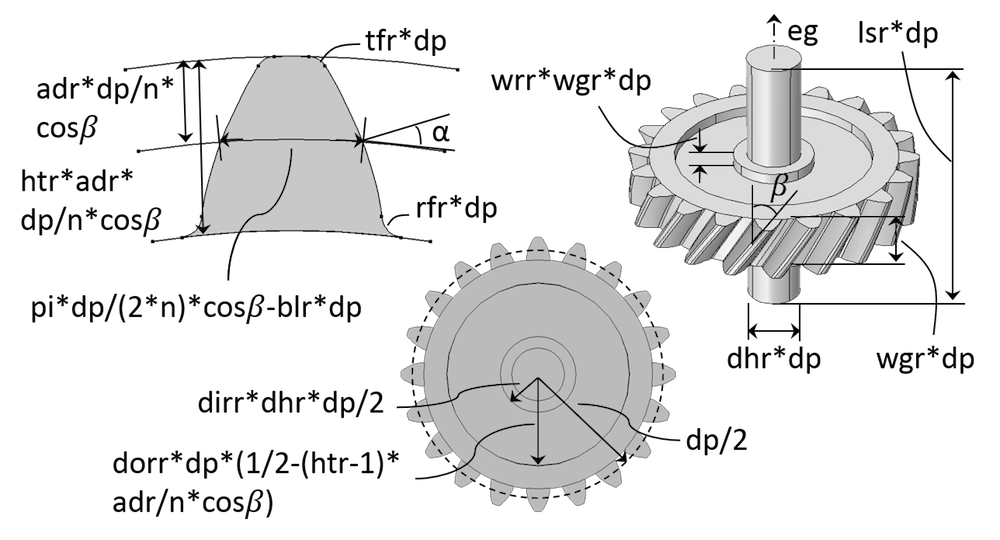
斜齿轮几何结构示意图，图中显示了多个输入参数。

上图中的输入参数和齿轮齿的输入参数一样也存在物理关系，我们可以利用这些输入参数计算齿轮参数，它们包括：

• 齿轮宽度：wg = wgr*dp
• 齿环宽度：wr = wrr*wg
• 齿环外径：dor = dorr*dr
• 齿环内径：dir = dirr*dh
• 轴长：ls = lsr*dp

在默认设置中，齿轮几何会应用一组特征。其中一些特征是可选的，只要将对应的输入参数设为零，即可移除它们，建立如下图所示的不包含轴、齿轮坯环、中心孔、齿尖圆角和齿根圆角的齿轮几何模型。

按照从（A）到（F）的顺序依次从直齿轮几何模型中移除了相应的可选特征。（A）默认的几何结构；（B）移除了轴；（C）移除了齿轮坯环；（D）移除了中心孔；（E）移除了齿尖圆角；（F）移除了齿根圆角。

在所有内置齿轮零件中，齿轮毛坯的形状都是一样的，不过我们可以通过移除齿轮材料在毛坯创建一个环。若想自行改造齿轮毛坯的形状，我们需要手动对内置零件的几何执行多次操作。

带自定义毛坯的齿轮。

齿轮零件库中的选择

内置的齿轮零件提供了许多选择，可以方便我们对物理场或后处理进行设置。这些选择除包含齿轮零件外，还有齿轮齿的边界。通过应用这些边界，我们可以模拟两个齿轮之间的接触。

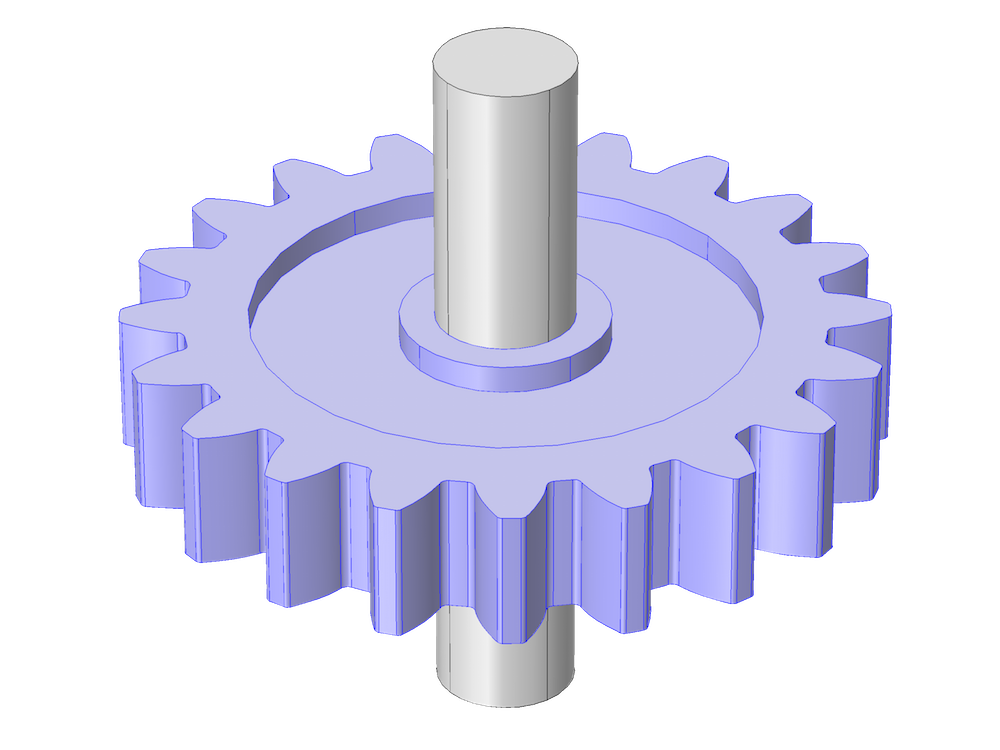
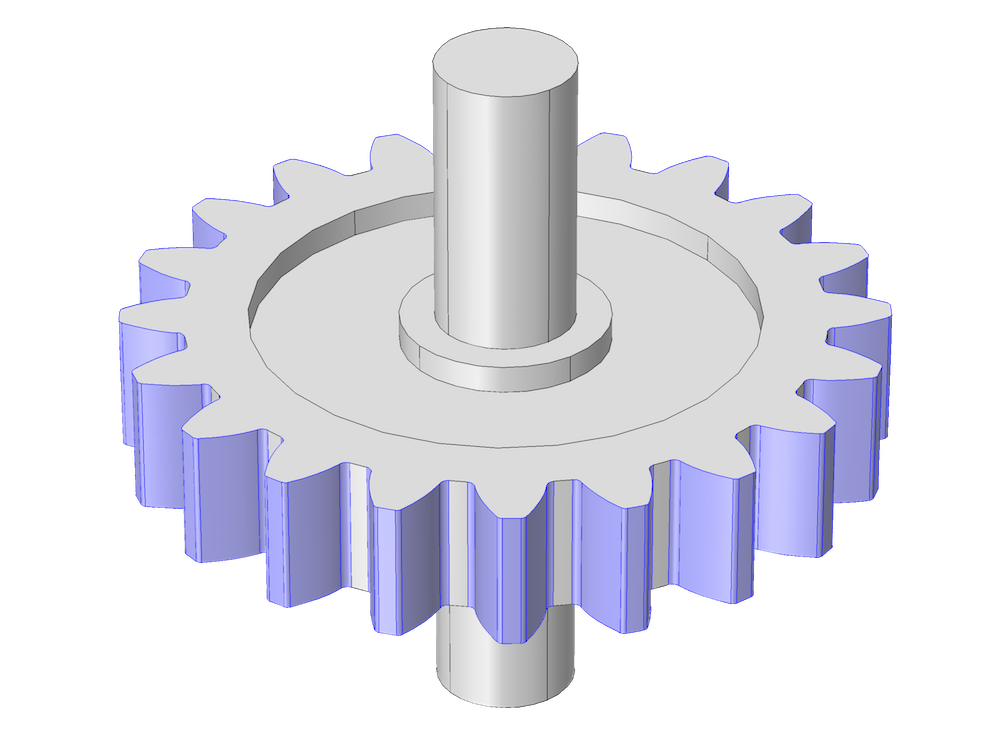
直齿轮的几何模型。左图突出显示了除轴以外的齿轮结构；右图突出显示了除齿轮齿边界和轴以外的齿轮结构。

检验及验证输入数据

软件中的齿轮零件是高度参数化的，所以一定要进行大量检查来验证输入数据。检查的目的是确保输入参数无论是独立使用，还是与其他参数组合使用时均正确无误。检查步骤应当在构建几何前进行。

当一组输入参数无效时，页面将提示对应的错误消息。举例来说，外齿轮的必要几何检查包括：

• 齿顶检查：ad<=(dp-db)/2
• 齿根检查：(2*dd/dp)<=0.9
• 孔径检查：dh<(dp-2*dd)

接下来，让我们了解一些基于内置零件创建的齿轮几何结构的示例。

应用案例：差动轮系

第一个示例是汽车中的差速轮系机构，轮系的左轴和右轴具有不同的旋转速度。差速轮系在工作状态下会用到五对锥齿轮（总共六对）。

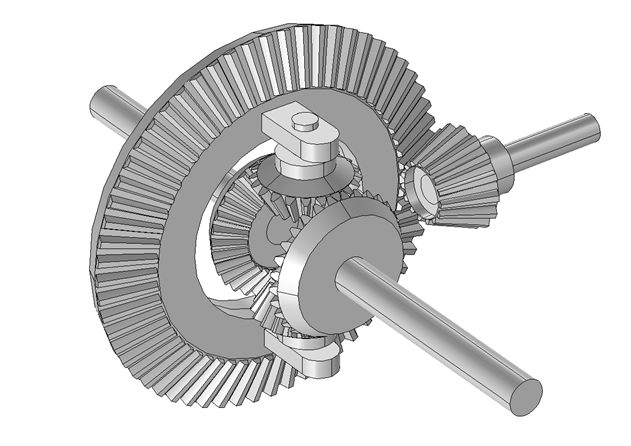
差动齿系机构的几何模型。

应用案例：三级风机齿轮箱

下面将介绍的示例是三级风机齿轮箱。第一级是行星齿轮系，它包含三个行星齿轮、一个太阳齿轮和一个环形齿轮。第二级和第三级是相互平行的齿轮系，每个齿轮系都由一对齿轮组成。该齿轮箱在运转时会使用到八对（总共九对）斜齿轮。此类齿轮箱的典型齿轮比从 50 至 100 不等。

风机齿轮箱的几何模型及其顶视图与前视图。

结束语

齿轮是一类可以传递运动和动力的机械元件，在汽车和风力涡轮机等各式各样的机械中均具有广泛的应用。借助 COMSOL Multiphysics 的新功能，我们可以高效地建立齿轮几何模型。利用这些强大、高度参数化的内置零件，可以自由地更改齿轮的形状，从而设计出适合特定应用的齿轮几何模型。

在“齿轮模拟”系列的下一篇文章中，我们将向您展示如何模拟变速箱的噪声和振动，敬请期待！此外，我们还为您准备了以下资源。

学习更多关于齿轮建模和多体动力学模块的知识

• 查看齿轮模拟系列中的其他博客文章
• 有兴趣学习多体动力学建模吗？请阅读“COMSOL 博客”中的相关文章
• 访问发布亮点页面，深入认识 COMSOL Multiphysics 5.2a® 版本新发布的齿轮建模特征和功能