
在改进半导体器件研发流程和制造技术的过程中,仿真具有巨大的应用潜力。通过仿真分析可以减少设计过程中所需的试验和制造次数。由于必须解决器件的长度尺度问题,以及半导体物理现象的非线性特性,对三维半导体器件进行建模具有一定的挑战性,往往需要进行计算量非常大的仿真工作。本篇博文中,我们将通过一个使用 COMSOL Multiphysics® 建立的三维双极晶体管的示例,介绍建立半导体器件三维仿真模型(以下简称半导体模型)的一般思路与步骤,并提出重要建议,希望对大家的建模工作有所启发。
双极晶体管
双极晶体管(注:一种电流控制器件,起放大、振荡、开关等作用)最初是在 20 世纪 40 年代末发明的,被广泛应用于第一批集成电路中。尽管在数字逻辑电路中,现代场效应器件已经基本上取代了双极晶体管,但双极晶体管仍广泛用于模拟应用。它们在功率调节电路中应用特别多,用作开关和电流放大器。
仿真注意事项
为了确保仿真能够有效地捕获所有必需的物理场,以得出准确的模拟结果,理解模型中需要包括的物理过程是很重要的。这些可能会根据器件的配置以及其将要运行的环境而有所不同。在最小化问题复杂性的同时,确保模型具有令人满意的可靠性和准确性始终是建模需要考虑的关键。
对于三维半导体仿真这尤为 重要,因为在三维半导体仿真中,使用非推荐技术创建的模型可能需要花费很多天才能求解,甚至可能永远不会收敛。
本文将通过建立双极晶体管三维模型的过程为您提供建模指导。首先,我们将介绍和解释半导体器件的运行以及必须包括的重要物理过程;然后,我们还将讨论有效地将物理场纳入模型所需的措施;最后,配置合适的研究并提取仿真结果。
掺杂结构和设备对称性
像许多半导体器件一样,掺杂对于双极晶体管的运行至关重要。掺杂有两种类型: p 型掺杂(其中一个区域具有额外的空穴)和 n 型掺杂(其中一个区域具有额外的电子)。
双极晶体管由三个交替的p型和n型掺杂区域组成。尽管有两种可能的掺杂结构,n-p-n 或 p-n-p,但本文我们将重点介绍 n-p-n 配置,因为这是最常见的一种结构。通过将 p 型层夹在两个 n 型层之间形成 n-p-n 结构。可以认为该器件具有三个不同的区域,分别称为发射极、基极和集电极。可以通过三个单独的金属触点分别对每个区域进行电寻址,这些触点根据它们所连接的区域进行标记。
下图为显示了 n-p-n 掺杂结构、设备区域和电连接的示意图:
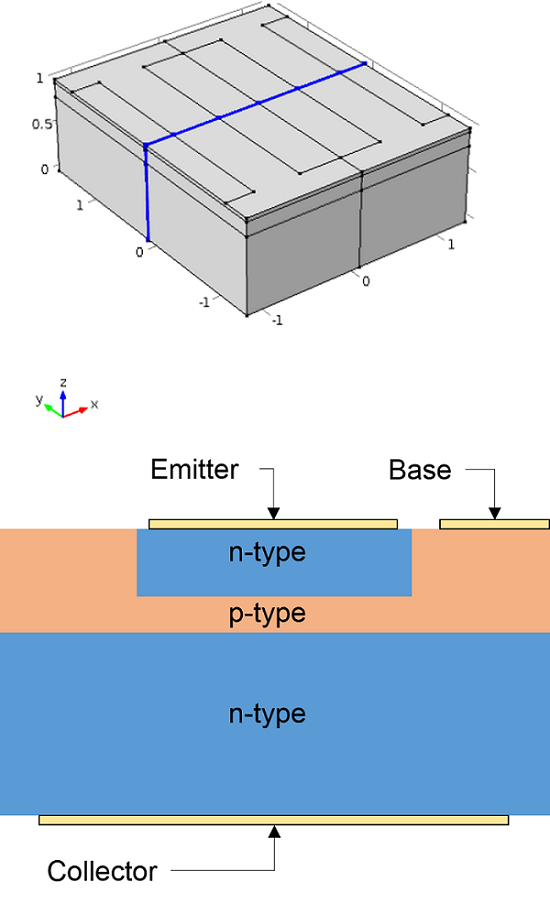
双极晶体管器件的几何形状和结构。顶部:使用 COMSOL Multiphysics 仿真软件模拟的双极晶体管器件的几何形状。底部:沿 z-x 平面截取的器件横截面,由蓝色边缘高亮显示的上部图像。标记了 n-p-n 掺杂图案以及连接到发射极、基极和集电极区域的电触点。
由于三个区域的交替掺杂,双极晶体管形成了两个紧挨着的 p-n 结,它们共享基极区。载流子通过这些 p-n 结时的行为对于双极晶体管的工作至关重要。
在本示例接下来的建模过程中,我们将以有效计算的方式,介绍能包含描述此行为所需的所有相关物理场的适当步骤。
对称平面
设计三维半导体模型时首要考虑的问题是:“我可以使用对称性来减小模型尺寸吗?”
许多类型的器件具有对称平面,绕轴旋转对称甚至轴对称几何。如果可能的话,建议使用轴对称设计,因为这样可以将三维仿真降低到二维。我们可以在 COMSOL 案例库中找到圆柱形场效应晶体管的轴对称建模示例。
在此示例中,我们要模拟的器件具有两个对称平面,这些对称平面在 x-z 和 y-z 平面中将设备一分为二。这意味着我们只需要对一个象限建模。如下图所示,右上象限被选为建模对象:
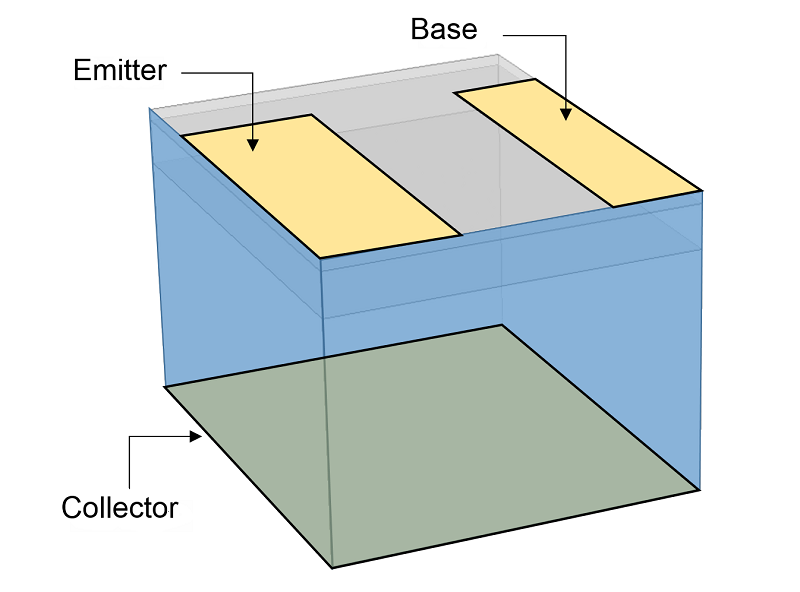
模型所需的几何。由于以蓝色突出显示的平面对称,因此仅需对器件的一个象限建模。这样可以减小模型的大小,从而可以在更短的时间内以更少的内存求解。如图所示,将金属触点应用于表面边界。
确保解析了掺杂分布
在创建对称性允许的最小模型几何形状之后,下一个需要考虑的问题是:“我需要什么样的分辨率才能可靠地捕获模型中的物理场?”
显然,器件的几何尺寸需要充分解析。但是,所需的物理过程通常发生在比器件几何特征小得多的长度范围内。对于半导体模型,确保足够的分辨率可能是一个挑战,因为涉及的各种物理过程通常需要差别很大的长度范围。更复杂的是,整个器件中充分描述许多过程所需的空间分辨率可能会有很大的变化,甚至可能随其他模型参数(例如外加电压)而变化。
对于上述难题,我们可以从确保解析了掺杂分布开始。这是因为在掺杂浓度快速变化的区域中,其他量也会经常发生剧烈变化。值得庆幸的是,确保掺杂分布得到解析是相对简单的,因为掺杂分布是由用户控制的,并且在其他模型参数发生变化时不会改变。
COMSOL Multiphysics 仿真环境提供了方便的工具,可以轻松查看整个设备中的掺杂。我们可以通过研究节点中的获取初始值 选项查看,因为掺杂浓度是可以在不求解半导体方程的情况下进行计算和可视化的解析函数。然后,绘制掺杂的初始值帮助整个计算建立合适的网格。
如下图所示,我们在整个模型中添加了掺杂的三维体积图,以及沿着器件中心的垂直切面截取的掺杂浓度的线切割。
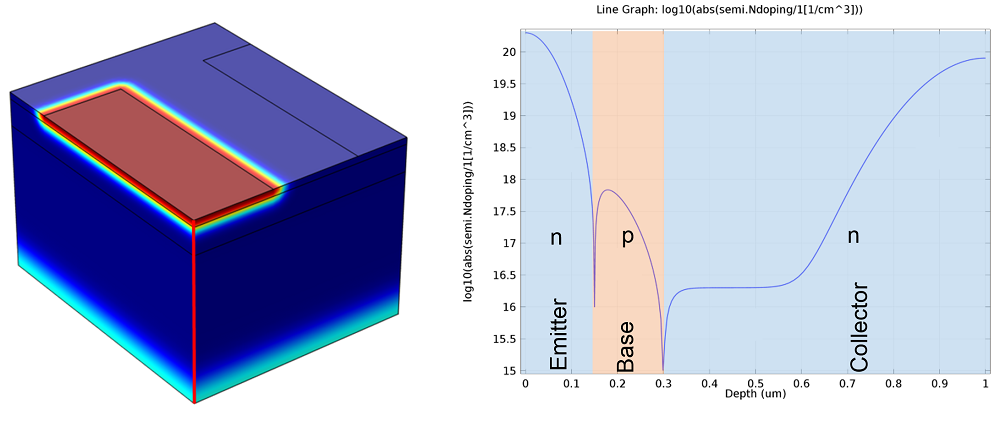
整个双极晶体管设备中的掺杂分布。左图:整个模型几何的三维可视化掺杂。前上角的红色区域是 n 型发射极区域。由于半导体器件中典型的掺杂浓度的数量级变化,因此很难看到三个不同的掺杂区。右图:沿着左侧图像中的红线截取的掺杂浓度的线切割。采用对数刻度,使 npn 掺杂图案清晰可见,并标记了每个区域。注意,掺杂浓度在每个区域内变化,但是掺杂浓度的最快变化发生在发射极–基极和集电极–基极 p-n结处。
创建有效的网格
在 COMSOL Multiphysics 中,使用 结构化的扫掠 网格对三维半导体进行仿真具有一定的优势。这是在几何体外部表面上的面网格扫过几何体积的地方,从而生成与扫掠方向棱柱对齐的网格单元。
如下图所示,可以在本文示例模型所使用的网格中看到这一点,其中在顶部表面生成了自由三角形网格,然后向下扫掠至底部表面。网格被结构化 使得整个器件中棱柱的高度发生变化,从而在需要高分辨率的区域中沿z方向收紧网格。
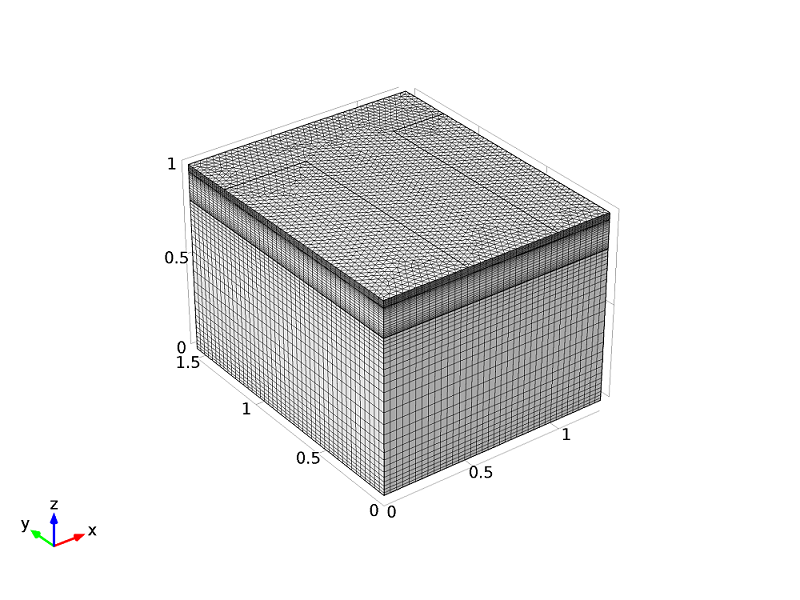
所使用的网格是结构化的扫掠网格,其中 z 方向的分辨率在 p-n 结附近且在顶部和底部表面上的电触点附近是最大的。
如上所述,重要的是细化掺杂分布梯度周围的网格。这是通过使用一个额外的嵌在主器件区域正下方的几何长方体实现的。放置额外的长方体,使得额外的内部边界位于掺杂浓度梯度最大的区域。这些内部边界用于控制网格的结构以将其在所需区域收紧。另外,对于半导体模型,最好在电触点附近收紧网格,以解析通常在其附近出现的高电流密度和电场效应。因此,在器件的顶面和底面附近还对网格进行了细化。
在掺杂梯度附近和静电边界附近细化网格是一个很好的开始。但是,如前所述,必须注意考虑模型中存在的物理过程,并修改网格以适应它们。
对于本文所模拟的双极设备,有源区分布在p-n结区域,除了确保 p-n 掺杂结构得到解析外,没有其他特殊的长度尺度可以考虑。但是,其他设备可能需要额外的考虑。例如,场效应半导体器件通常需要在表面栅极接触下进行非常细化的网格划分,因为在这些栅极下方的细通道区域中存在非常强烈的电流密度(详请参见此模型案例)。
如有疑问,最好考虑的量是德拜长度,它是高电荷密度区域的最小长度。最后,与任何数值仿真一样,重要的是评估 COMSOL Multiphysics 模型以确保解独立于网格。我们可以通过参数化网格密度并使用辅助扫描更改参数来方便地实现此目的。
对于三维半导体模型,建议在继续创建完整模型之前进行一些初步研究,以确认合适的网格分辨率。例如,我们可以模拟二维横截面,以了解德拜长度,并在升级到完整的三维版本之前测试网格的独立性。
捕获相关物理场
根据预期的应用,半导体器件可以在各种不同的配置下工作。由于三维半导体仿真的计算量很大,因此建议仔细考虑相关的应用并设计模型以得到合适的解。
在 COMSOL Multiphysics 中建立半导体模型时,问自己以下问题会很有用:“什么物理场对我的半导体有重要影响?”。
对于三维半导体模型,添加附加物理效应会迅速增加计算时间,因此尽量将模型限制在重要的过程中。例如,当对其中绝大部分电流由电子携带且空穴没有明显参与的器件进行建模时,它可能只适合于求解电子而不是同时求解电子和空穴。或者,在对连接到非常有效的散热器器件进行建模时,模拟温度变化的影响可能并不重要。
以下是我们使用 COMSOL 中的模型开发器建立双极晶体管示例模型的屏幕截图。除了默认节点以外,我们还使用了三个域特征来创建掺杂结构,并使用边界特征将触点分配给适当的边界。为了正确地解释通过这种高掺杂设备的电流,还增加了陷阱辅助复合 特征。但是,不包括其他物理过程。
双极晶体管模型示例的模型开发器。
传感电路的电流放大
双极晶体管器件的常见工作模式是将发射极接地,并将电压分别施加到基极和集电极区域。下图所示的这种配置适合于将双极型晶体管用作电流放大器。下面,我们将对该配置进行建模。
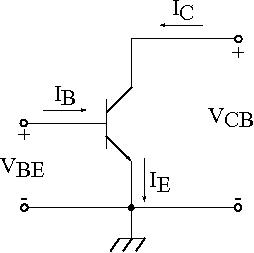
电路图显示了共发射极配置中的双极晶体管。
少数载流子的重要性
此工作模式测量得到了相对于接地发射极的基极和集电极电压,因此这种设置称为共发射极配置。
在共发射极配置中,可以通过向基极施加电流来改变发射极和集电极之间的有效电阻。这使该器件可以用作电流放大器。这是因为在集电极和发射极之间流动的电流的大小(在给定的集电极-发射极电压下)与在基极和发射极之间流动的电流成正比。
从集电极输出的电流与施加到基极的电流之间的比率称为电流增益。典型的双极晶体管的电流增益超过 100,使集电极电流输出可以由输入基极电流控制,该基极电流比所需的输出电流小 100 倍以上。这使得双极晶体管在广泛的电源管理应用中具有吸引力。
一种常见的应用是使用来自某些感应电路的小电流来控制流向更高能耗组件的电流。例如,由温感电路产生的小电流可用作输入,以控制加热元件供电所需的较大输出电流。对于特定的应用,我们可以考虑相关的物理过程,以确保我们的模型添加了正确的特征并得到充分的解析。
双极晶体管因依赖电子和空穴电流工作而得名。这与单极晶体管(例如通用金属-氧化物-半导体场效应晶体管 (MOSFET)设备)相反。在单极晶体管中,电流仅由一种载流子物质所运载。因此,在模拟双极型设备时,对电子电流和空穴电流进行建模非常重要。
为了理解 n-p-n 双极晶体管的工作原理,需要考虑构成器件的两个 p-n 结以及施加到每个 p-n 晶体管的偏压方向。当用作电流放大器时,基极和集电极触点处的电压相对于接地的发射极触点为正,并且集电极触点处的电压比基极触点的电压幅值更大。这被称为正向激活 状态。
在正向激活状态下,正向偏压被施加到发射极-基极结处,而反向偏压被施加到集电极-基极结处。发射极-基极结处的正向偏压允许热激发的载流子从发射极注入基极区域。因为 p 型区具有丰富的空穴,但电子很少,从 n 型发射极区进入到p型基极区的电子被称为少数载流子。少数载流子电子从邻近发射极-基极结处的高浓度扩散通过基极区域到较低浓度的 p 型基极区域。然后,在反向偏压的集电极-基极结附近移动的少数电子被集电极-基极结的电场驱动到集电极触点。但是,基极区域中的大多数空穴不能穿透反向偏压结。总体结果是,电子电流可以在发射极和集电极触点之间流动,穿过所有三个区域,而空穴电流被限制在基极和发射极区域。
评估相关物理场
现在,我们已经知道了我们期望器件如何工作,那么就可以检查模型中是否包含重要的物理场以及是否得到充分解析。
我们已经细化了掺杂梯度周围和触点附近的网格,以考虑大多数半导体模型共有的预期物理特性。这将确保 p-n 结以及相关的电场得到正确解析。唯一要考虑的附加物理过程是少数载流子在整个基极区中的扩散。这是一个重要的物理过程,因为它会显著影响设备的性能,并且在设计或优化双极晶体管时可能会引起关注。
例如,与电子扩散长度相比,基极区必须足够薄,以便电子可以使其进入集电极区,但又不能太薄,以至于电子和空穴直接从发射极隧穿到集电极中。碰巧,载流子扩散已经包含在标准的半导体方程组中,并且与基极区域中的电子扩散长度相比,网格已经相当精细。因此,此特定模型不需要任何特殊的修改。
选择适当的研究并提取结果
最后要做的是配置合适的研究,以在与器件正常工作相关的条件下对器件进行模拟。这是我们需要问自己:“我模拟的器件的典型工作条件是什么?”。
通常,半导体器件可以针对不同情况以不同的配置进行布线。但是,出于计算时间的考虑,模拟所有可能的工作条件可能不切实际。例如,与运行覆盖所有可能的电压组合的电压扫描不同,我们可以将研究限制为仅求解典型工作期间遇到的电压组合和扫描范围。
此外,我们还需要考虑想从模型中获得什么信息并设计研究,以便从解中提取这些信息。本文的示例模型有两项研究:一项研究将集电极电压设置为 0.5V 并扫描基极电压,另一项研究将基极电流设置为 2μA 并扫描集电极电压。第一项研究允许我们轻松计算电流增益。第二项研究允许我们将发射极-集电极电流计算为固定输入基极电流的发射极-集电极电压的函数。
计算电流增益
第一项研究可用于生成被称之为根梅尔图 的绘图。这是评估用作电流放大器的双极晶体管的标准方法。它以对数 y 轴刻度显示集电极电流和基极电流与基极电压的函数关系。电流增益可以用集电极电流与基极电流之比表示,这是放大器设备的关键性能参数。
下图为一个根梅尔图绘图。从该图判断,在整个基极电压范围内,集电极电流比基极电流大两个数量级。
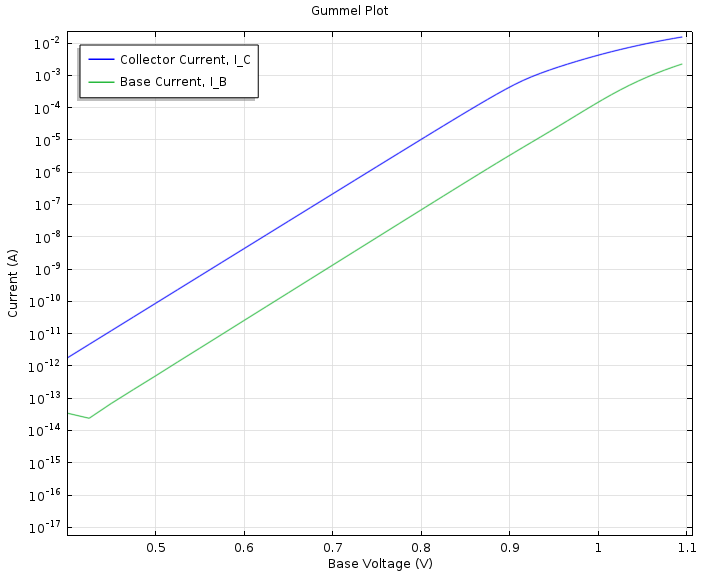
根梅尔图显示了在将 0.5V 电压施加到集电极时,集电极和基极电流与基极电压的函数关系。
接下来,我们有一个图,该图显示了作为集电极电流函数的电流增益。在 9 个数量级的集电极电流范围内,电流增益相当恒定,约为 160。但是,对于集电极电流大于 1mA 的情况,电流增益会急剧下降。该仿真表明,如果在集电极-发射极压降为 0.5V 的应用中用作电流放大器,则该器件的工作极限约为 1mA。
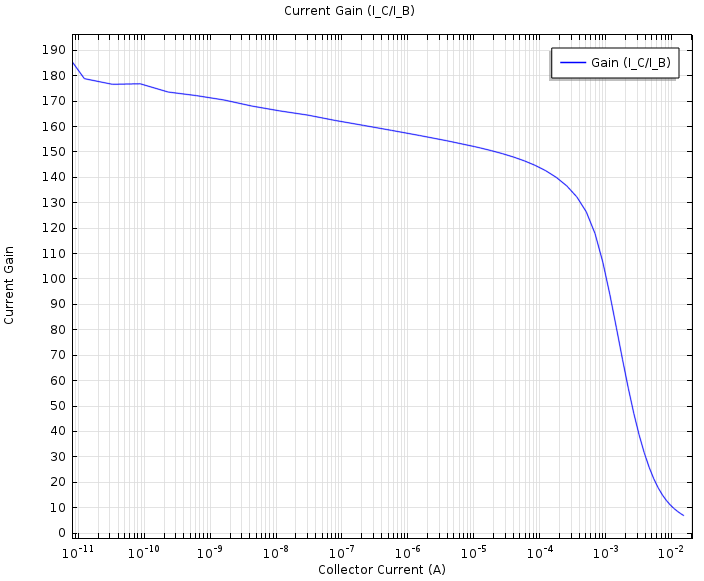
双极晶体管的电流增益是集电极-发射极压降为 0.5V 时集电极电流的函数。
需要注意的是,可以在不同的集电极电压范围内进行相同的研究和分析。然而,由于如上所述涉及的计算费用,建议将该范围缩小到正常使用期间的预期工作电压。
共发射极输出特性和载流电流
如下图所示,第二项研究用于在施加 2μA 的输入基极电流时生成集电极电流随集电极电压变化的曲线图。最初,集电极电流会随着集电极电压的增加而迅速增加,然后在 300μA 左右达到饱和。
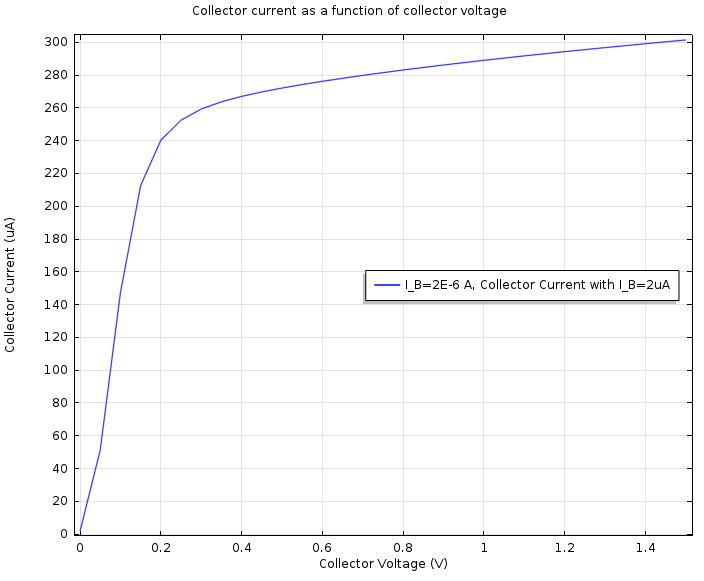
当向基极施加 2μA 的输入电流时,集电极电流随集电极电压的变化而变化。
从类似器件的二维仿真示例可以看出,饱和电流水平由输入基极电流控制。这是一个将二维模型与三维模型结合使用以使器件建模更加有效的示例。在进行完整的三维设备仿真之前,最好使用二维模型观察一般行为并确定参数组合或感兴趣的范围。
最后,使用完整的三维仿真,我们可以对器件内的三维电流实现可视化。最后一张图显示了集电极电压为 1.5V,输入基极电流为 2μA,处于饱和状态的电子电流(黑色箭头)和空穴电流(白色箭头)的箭头图。彩色图切面显示了电压,使我们能够看到 p-n 结。正如预期的那样,空穴电流不会横穿集电极区域,而电子电流主要在集电极和发射极之间流动。
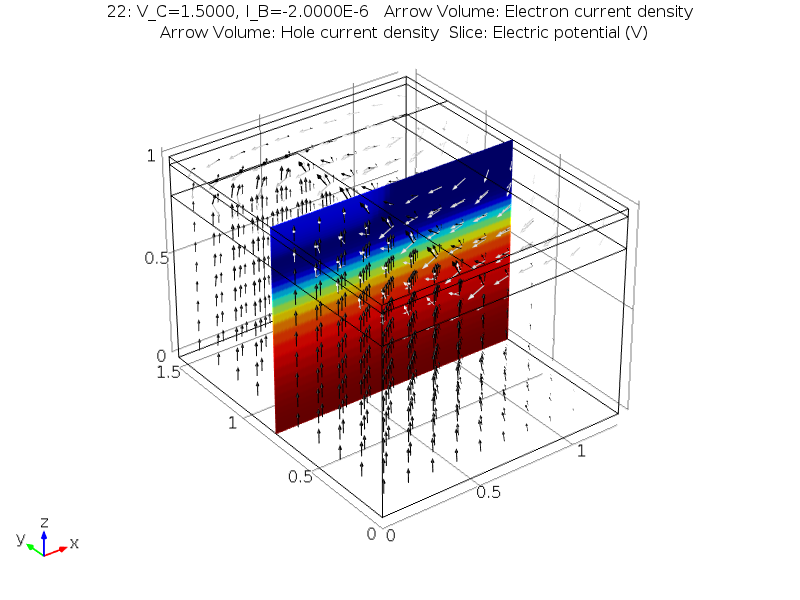
在集电极电压为 1.5V 且将 2μA 输入电流施加到基极的情况下,流过双极晶体管的电流的三维可视图。电子电流用黑色箭头显示,空穴电流用白色箭头显示。切面的颜色代表整个器件的电压。
结语
文中演示的示例模型是使用 COMSOL Multiphysics 软件建模和分析三维半导体器件的建模实践。尽管本文研究的器件相对简单,但是相同的思维过程和模型构建步骤可以应用于任何半导体模型。虽然三维半导体建模仍然是一个具有挑战性的计算领域,但本文提出的建议可以指导您如何开始创建有用的器件模型。
拓展资源
- 有关 COMSOL Multiphysics 模型库中的示例双极晶体管模型的更多详细信息,请参见:
- 有关此模型使用的某些物理场的更多信息,请参见:






评论 (0)