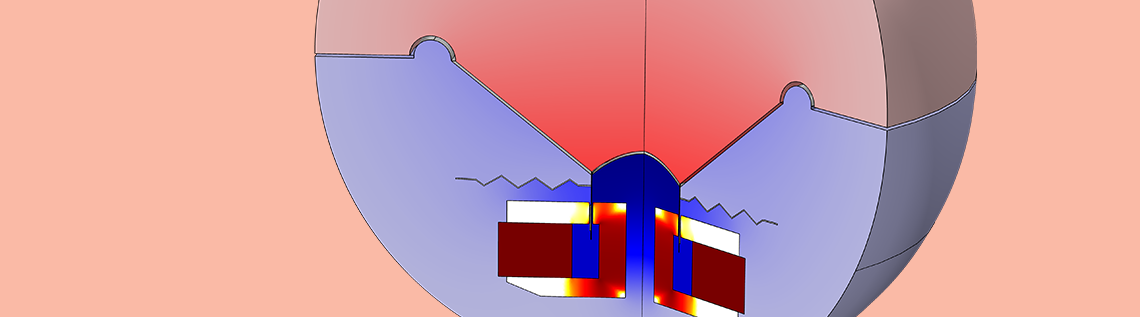
扬声器驱动器的全面分析不仅限于频域研究。一些我们需要或不需要(但仍令人着迷)的效应只能通过非线性时域研究来捕获。在本文中,我们将讨论系统非线性如何影响声音的生成,以及如何使用 COMSOL Multiphysics® 软件对扬声器驱动器执行非线性失真分析。
认识线性和非线性失真
换能器可将具有一种能量形式的信号(输入信号)转换成具有另一种能量形式的信号(输出信号)。扬声器属于电声换能器,在动圈式扬声器中,输入信号是驱动音圈的电压。输出信号是被人耳感知为声音的声压。失真现象指的是输出信号与输出信号产生量与/或质上的差别。
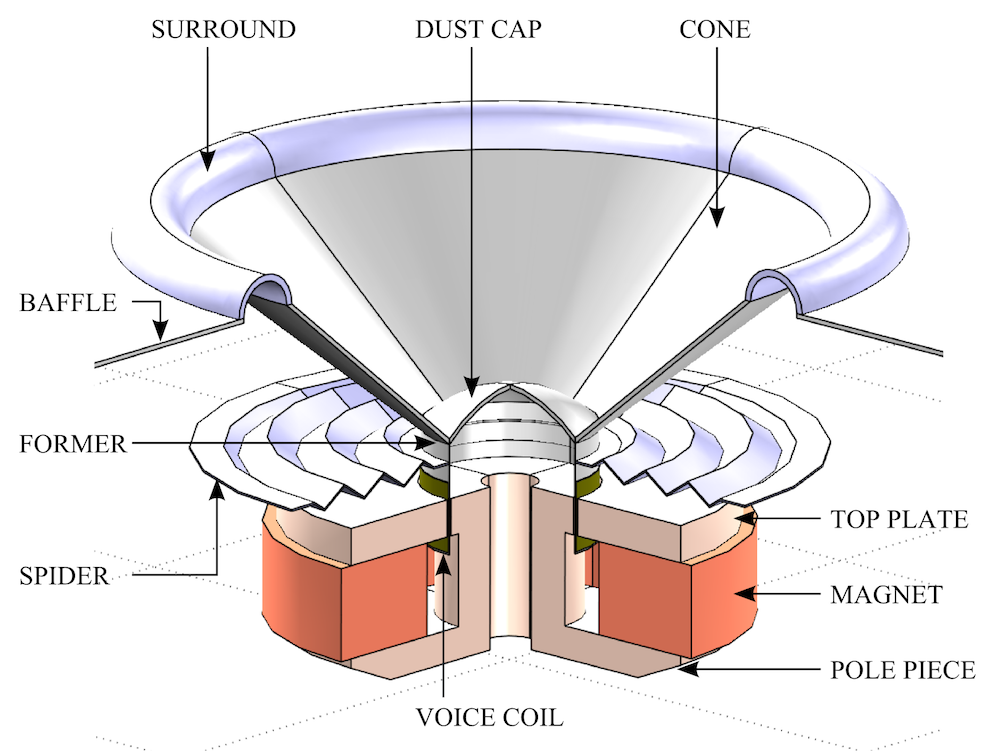
动圈式扬声器的示意图。
失真主要分成两种:
- 线性失真
- 非线性失真
线性失真,这个让人不明所以的专业词汇表明输出信号与输入信号具有相同的频率组成。在线性失真中,失真对象是输出信号的幅度和/或相位。非线性失真 则暗示输出信号包含输入信号中不存在的频率组成。这意味着输入端为单一频率的能量到达输出端时产生了多个频率。
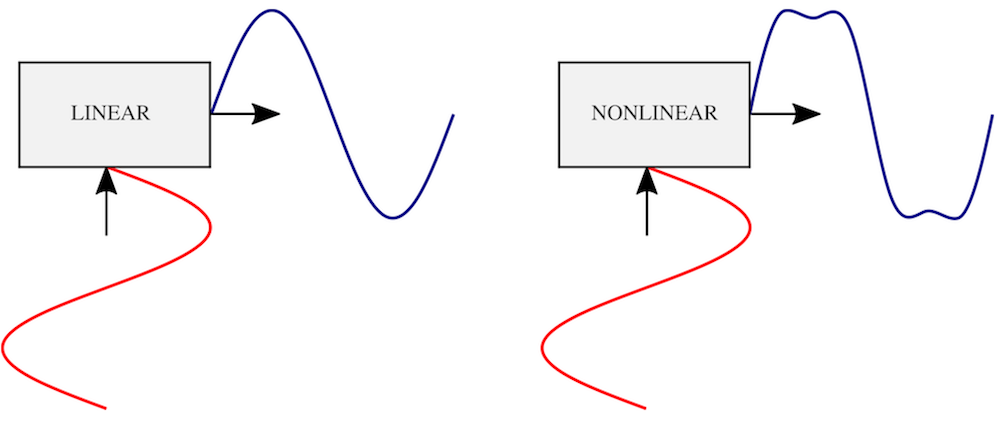
线性和非线性换能器的输入和输出信号。
将正弦信号 A_\text
{in} \sin \left( 2\pi f t \right) 应用于采用非线性传递函数的换能器后,输出信号将由多频组成。除了与频率 f 对应的信号基本部分之外,还存在着失真部分。它的频谱通常(但不总是)由频率 f^{(2)}, f^{(3)}, f^{(4)}, \ldots 组成,这些频率均为基频的倍数,即 f^{(n)} = n f,其中 n \geq 2。这些频率存在于声音之中,被称为泛音。泛音赋予了乐器与众不同的音色:小提琴弹奏的乐声听起来与吉他迥然不同。扬声器发出的声音亦是如此。
失真是一个相对量,可以通过总谐波失真(total harmonic distortion,简称THD)的值来描述,该值为信号失真部分与基本部分的大小比:
具有较高 THD 值的信号的轮廓明显不同于纯正弦波信号。
不幸的是,输出信号本身的 THD 值可能不足以作为判断扬声器质量的依据。THD 值较小的信号可能听起来比 THD 较大的信号差,原因是人耳能够以不同的方式感知各种泛音。
失真可以被表征为一组单独的偶数阶分量 2nf 和奇数阶分量 (2n-1)f。前者是由于换能器的非对称非线性,而后者是由于对称非线性。事实上,含偶数阶谐波的声音被公认为“甜蜜”又“温暖”的声音。八倍基频。含奇数阶谐波的声音则“刺耳”又“粗粝”。这是吉他失真效果器所追求的效果,但不适合扬声器。当然,重要的不只是谐波本身的存在,而是它们在输出信号中的水平。
当输入信号包含多个频率分量时,将发生另一种有趣的效应——互调。对应的输出信号彼此相互作用,产生了输入信号中不存在的频率分量。实际上,如果将诸如 A_\text{in}
\sin \left( 2\pi f_1 t \right) + B_\text
{in} \sin \left( 2\pi f_2 t \right)(其中 f_2 > f_1)的双频正弦波应用于输入,系统非线性可导致较高频率分量被较低的频率分量调制。也就是说,f_2 \pm f_1、f_2 \pm 2f_1 等频率将出现在输出信号的频谱中。频率 f_2 \pm (n-1) f(其中 n \geq 2)对应的互调的定量测量值是 nth 阶互调失真(intermodulation distortion,简称 IMD)系数,其定义为:
在实践中,不建议使用包含三个或以上频率的输入信号进行 IMD 分析,因为结果将变得难以解释。
扬声器驱动器的瞬态非线性分析
总而言之,虽然扬声器的线性分析是助力设计人员的强大工具,但这还不够。我们需要引入其他非线性分析,才能完整地描述扬声器。非线性分析应该回答以下问题:
- 扬声器的非线性行为如何影响输出信号?
- 确保扬声器正常运行的输入信号的极限是什么?
- 应该如何补偿扬声器的不良失真?
从仿真的角度来看,既有坏消息也有好消息。坏消息是我们无法在频域中执行完整的非线性分析,所以需要对扬声器进行瞬态仿真,然而瞬态分析比频域分析更加费时费力。好消息是某些非线性仅在低频下产生显著影响。
举例来说,音圈在低频下的位移较大,因此必须使用有限应变理论来模拟电动机的机械零件。较高频率更适合采用无穷小应变理论,有限应变理论过于冗余。下图显示了扬声器瞬态分析教程的结果,扬声器由相同大小的输入电压驱动(V_0 = 10 V):
\left( t \right) = V_0 \sin \left( 2 \pi f t \right)
在单频输入电压信号下,音圈在扬声器驱动器气隙中的运动:左侧频率为 70 Hz,右侧为 140 Hz。
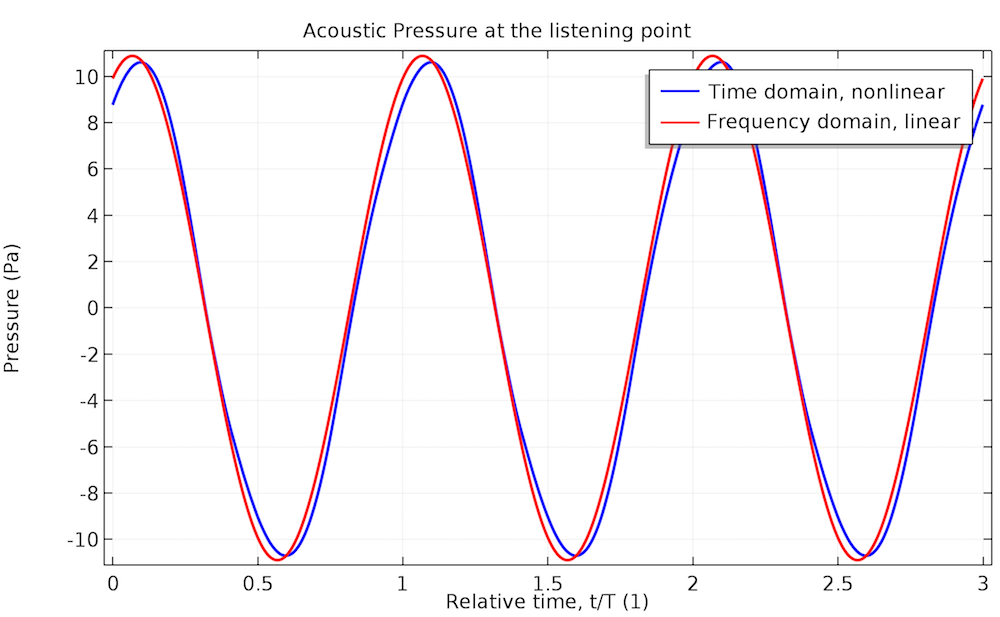
单频输入电压在聆听点上的声压。蓝色曲线对应于非线性时域分析,红色曲线对应于频域分析:左侧为 70 Hz,右侧为 140 Hz。
上方动画展示了音圈气隙中的磁场,以及磁场、弹波(均为粉色)与音圈(橙色)的运动。正如所料,位移与弹波变形在低频下更明显。弹波变形符合几何非线性分析,因此在此例中线性近似是不准确的。输出信号图证实了这一点。这些绘图描述了位于扬声器防尘帽顶端前方约 14.5 cm 处的聆听点处的声压。
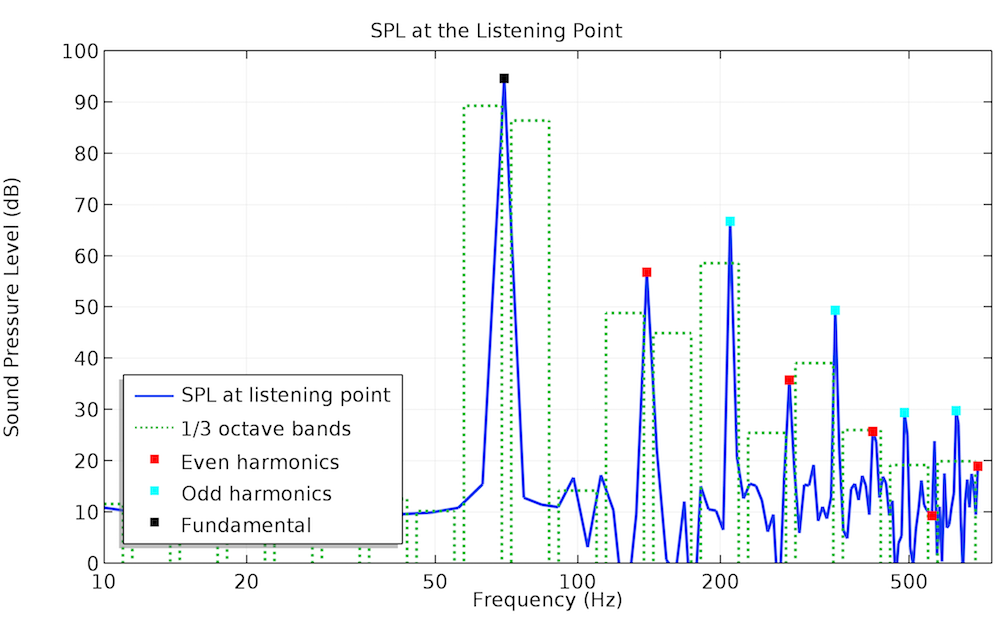
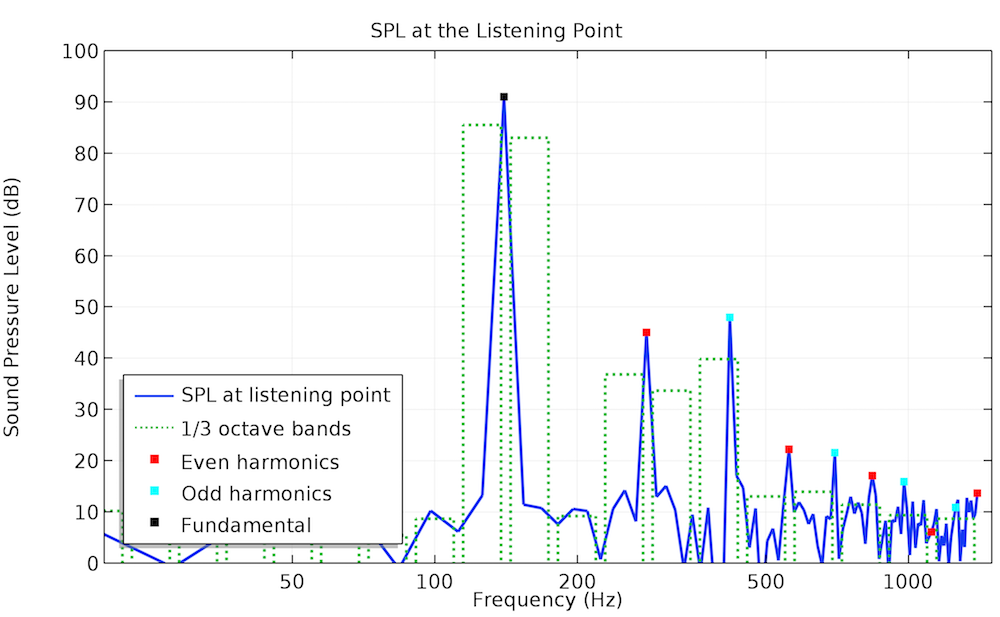
借助对 70 Hz 的输入信号进行非线性时域建模,所生成的声压分布在一定程度上偏离了正弦曲线形状,这意味着高阶谐波开始发挥一定的作用。至于 140 Hz 的输入信号,我们看不到这种情况:线性频域与非线性时域的仿真结果的量值只存在细微差别。输出信号的 THD 值在第一种情况中为 4.3%,第二种情况下降为 0.9%。下图显示了谐波如何影响聆听点的声压级(SPL)。
聆听点处声压级的频谱:单频输入电压(左侧为 70 Hz,右侧为 140 Hz)。
扬声器的 IMD 分析以相似的方式进行。不同之处在于施加于音圈的输入信号,它包含两个谐波部分:
{in}
\left( t \right) = V_1 \sin \left( 2\pi f_1 t \right) + V_2 \sin \left( 2\pi f_2 t \right)
V_1 和 V_2 的大小通常为 4 : 1,相当于 12 dB。
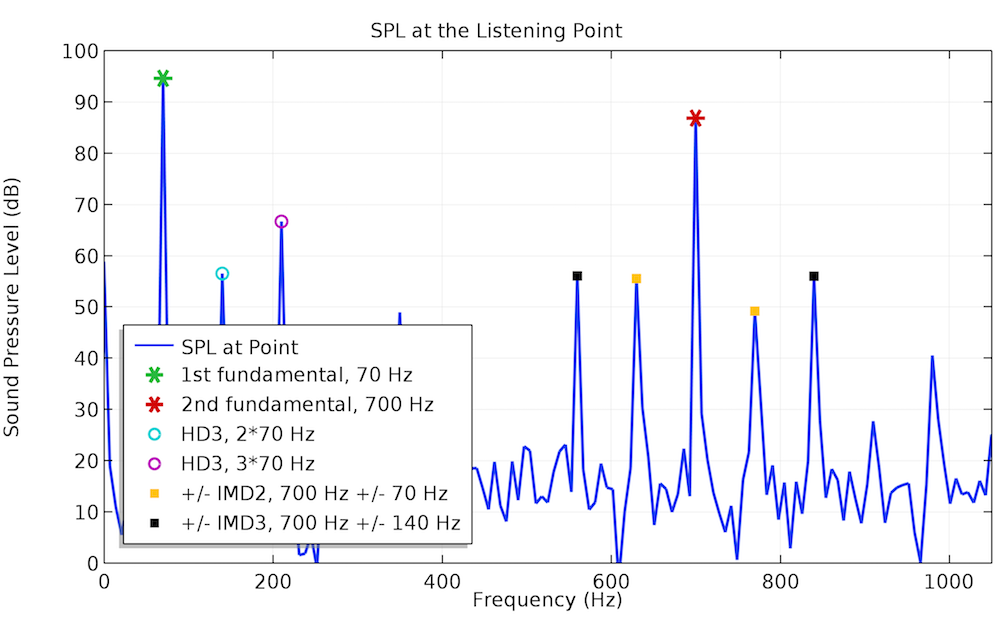
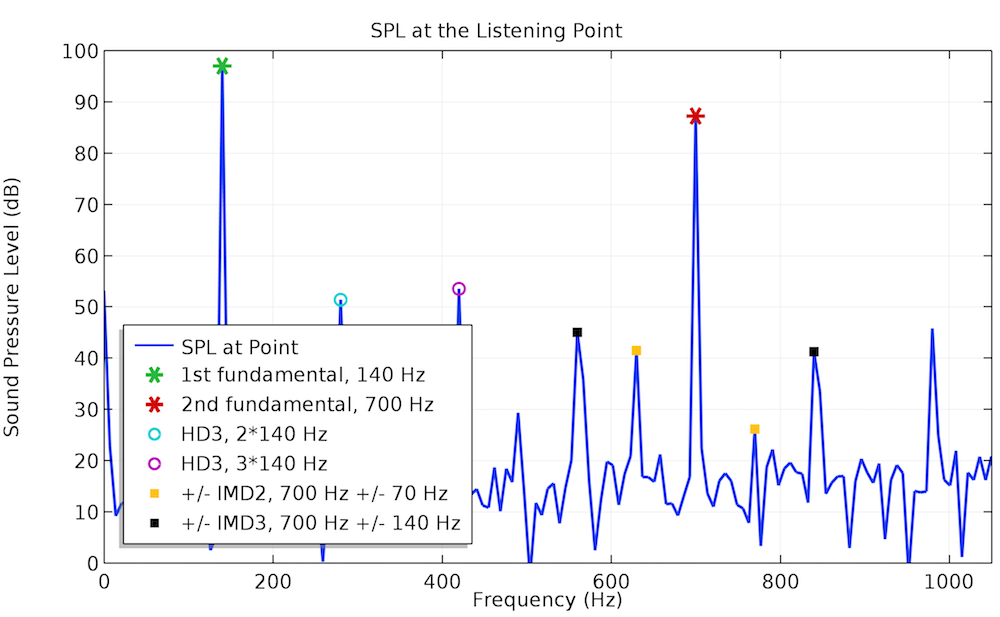
下方示例研究了相同的扬声器测试驱动器的 IMD。双频输入电压(f_1 = 70 Hz 和 f_2 = 700 Hz)充当输入信号。左侧的 SPL 图显示了出现在输出信号低频部分中的二阶和三阶谐波如何在高频部分中产生相当大的等阶次 IMD。如果信号频率 f_1 增加到 140 Hz,IMD 水平将变得足够低,如下方右图所示。
双频输入电压的声压级在聆听点的频谱。
分析扬声器驱动器的建模技巧
由于瞬态非线性仿真往往费时费力,因此扬声器驱动器模型不宜过于复杂。二维轴对称公式是一个很好的起始方法,上一节的教程示例便采用了此方法。之后,我们需要估计哪些效应相比于其他效应更为重要,这有助于创建恰当的扬声器多物理场模型。
系统非线性包括但不限于以下行为:
- 由高磁导率金属制成的扬声器极片的磁场的非线性行为
- 电机活动部件的几何非线性
- 当音圈在气隙中上下移动时的拓扑变化
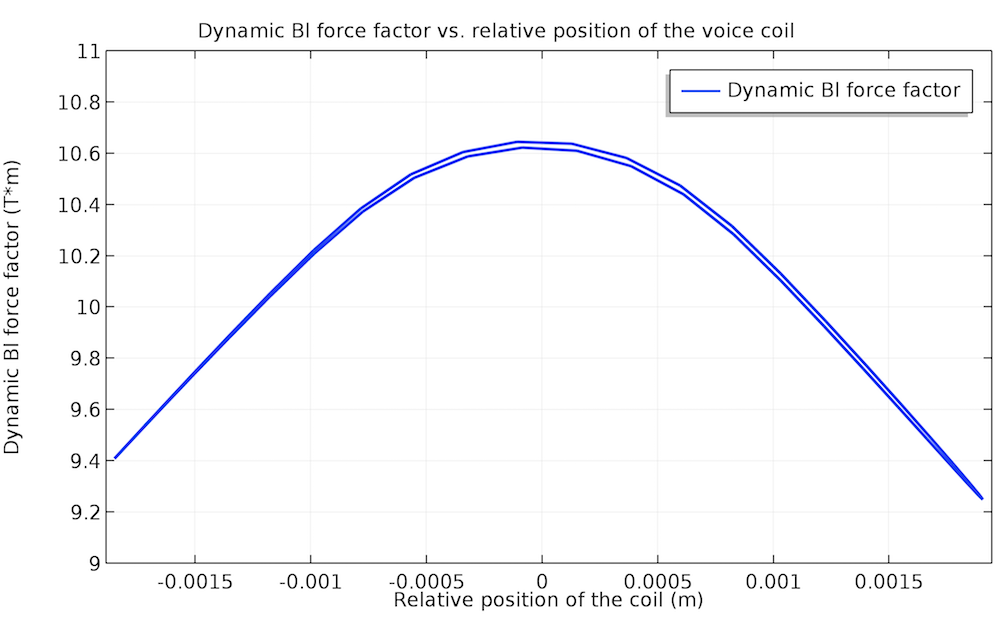
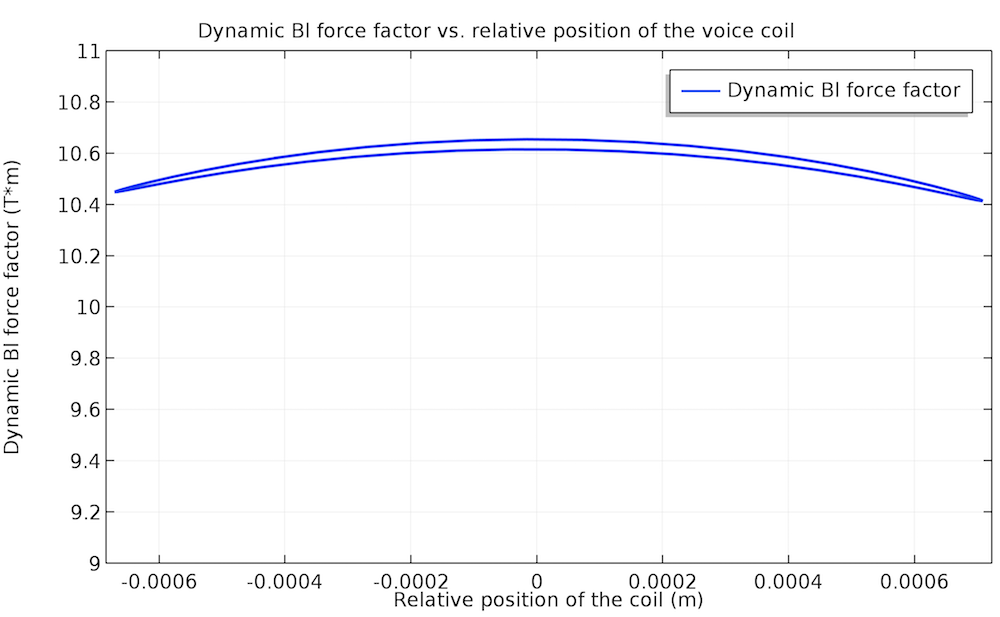
既然采用了集总参数,这意味着它们不再是类似于 Thiele-Small 参数的常数,而是音圈位置 x 和输入电压 V 的函数。上述非线性将反映在非线性电感 L \left( x, V \right);声顺 C \left( x, V \right);和动力因子 Bl \left( x, V \right) 中。在教学示例中,动力因子的非线性行为在 70 Hz 时更加明显,但在 140 Hz 时几乎是平坦的(即更接近线性)。
动力因子的非线性(左)和近似线性(右)行为:左侧为 70 Hz,右侧为140 Hz。
下列步骤可以将非线性耦合到模型中。首先,利用对应材料的本构关系,引入非线性磁效应。在测试示例中,为铁极片选定 BH 曲线选项。接下来,研究设置 栏下的包含几何非线性 选项可确保模型的结构部分遵循有限应变理论。最后,动网格 功能可以捕获拓扑变化。只要应用了这项功能,它都能保证网格单元节点与系统的活动部分一起移动。由于位移可能非常大,因此网格单元变形可能达到极限水平,同时数值模型变得不稳定。自动重新划分网格 选项可用于解析高度变形的网格单元。
总而言之,扬声器的非线性时域分析比线性频域研究更加耗费努力和耐心。尤其是当模型采用了动网格 功能,并激活了自动重新网格化 选项时。因为动网格对网格质量非常敏感,所以在几何和网格预处理方面投入的时间将给予我们相应的回报。也就是说,必须避免高度变形的网格单元以及几何实体之间出现接近零的角度。正确选择用于重新划分网格的条件 选项可能还需要经历一些试错。
对于大多数标准而言,本文讨论的扬声器设计可能算不上“高质量”。奇数阶谐波在输出信号的频率组成中占据优势。
后续操作
如希望尝试对扬声器进行非线性失真分析,请单击下面的按钮,跳转至“案例下载”页面,您可以下载此模型的 MPH 文件以及详细的建模操作说明。(注意:您必须拥有 COMSOL Access 帐户和有效的软件许可证。)
更多资源
- 查看相关教程中的扬声器建模示例:
- 延伸阅读:
- L.L. Beranek and T.J. Mellow, Acoustics: Sound Fields and Transducers, Academic Press, 2012.
- Brüel & Kjær, “Audio Distortion Measurements,” Application Note BO0385, 1993.
- W. Marshall Leach, Jr., Introduction to Electroacoustics and Audio Amplifier Design, Kendall Hunt, 2010.




评论 (0)