
假设你需要分析一条横截面不变的超长系统——充液管道,却发现这类系统的建模工作不仅占用大量计算资源,而且极其耗时。利用导波传播方法,你能够模拟管道系统的横截面,同时计算管道中的导波。导波可通过色散曲线来表示。在本文中,我们将以空气和水作为管内流体进行耦合分析,并计划利用色散曲线分析系统的动力学。
充液管道:一个建模难题
充液管道又称液体输送结构,拥有广泛的工业应用,例如我们熟悉的输气管道、汽车消声器、飞机机身和水下管道。管道系统的尺寸短至几厘米,长至数千米。



充液管道的常见应用。左:海底管道,图片由美国大峡谷国家公园提供,已获 CC BY 2.0授权,并通过 Flickr Creative Commons共享。中:飞机机身模型。右:汽车消声器,图片由 lw5315us 提供,已获 CC BY-SA 2.0授权,并通过 Flickr Creative Commons共享。
大型管道系统难以使用仿真软件进行建模。再者,由于声学模态和弹性模态相互依存,逐个分析并不能降低难度。所以,我们的分析重点是流体载荷对管道结构响应的影响。
在低频下,流体载荷很小,因此系统响应取决于结构/管道的动力学(等式2)。流体载荷改变了接触结构的振动特性,进而改变了声辐射。由于流体力与流体的平均密度成正比,所以在与大密度流体接触的结构中,流体载荷的影响最为显著。
什么是色散曲线?
一般情况下,系统可以通过质量和刚度分布来描述。连续系统拥有无限个自由度(degrees of freedom,简称 DOF),这就产生了无限个模态。在有限频率范围之内,支持通过模态分解进行逐个分析的模式数量是有限的。此类连续系统,使用的是基于力与加速度以及力与变形关系的偏微分方程(partial differential equation,简称 PDE)来描述其运动。绳子、杆和轴(二阶 PDE)以及梁(四阶 PDM)和充液管道是一些常见的连续系统。
这些方程的解有两种绘制方式:
- 特征模态
- 波形式(或波模式)
假如使用有限元法(finite element method,简称 FEM)来模拟大型系统的高频动力学。为了捕捉其行为,必须使用足够多的单元对波长进行离散化处理,这就产生大量自由度,必然占用更多内存和时间。因为波在衰减前的传播距离相当长,所以我们可以通过使用波模态或者将系统表征为导波来解决这一问题。
声波性质是波动法的另外一个优点。波的性质对于研究结构噪声和有限长波导的频率响应、计算结构的能量传递十分重要。这些波形描述了波数和频率之间的关系,因此可利用色散曲线来表示。
色散曲线基本上是一根根独线,每根代表单个模态。波动法唯一的先决条件是系统的横截面必须始终不变(长度无限制)。波动法是模拟液体输送管道、梁或轨道等长距离系统的实用工具。
利用色散曲线分析充液管道
波在时空中传播。我们用表示单位距离内相变的物理量描述空间变化,它等于 ω/c。这是用k 表示的波数。一个波长相当于随 x变化的2π相差:kλ = 2π。
当系统一端受力时,大量波开始向另一端传播。每个波的传播速度被描述为相位速度(与ω无关,比如径向剪切波)和群速度(受频率影响,比如弯曲波)。所有波在包络内运动。能量的传递速度根据群速度计算出,而群速度是根据 cg = ∂ω/∂k 计算出的包络速度。
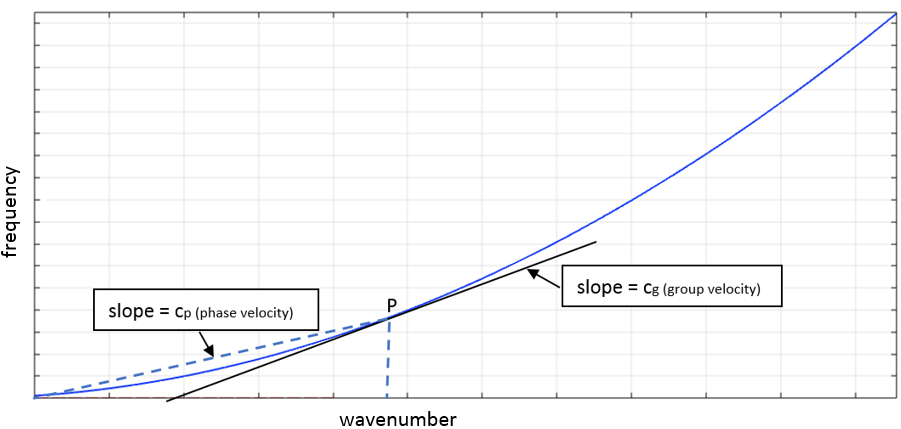
色散曲线示意图。
色散曲线解释了耦合系统的动力学。在充液管道内,波可以同时在液体和管壁中运动,而色散曲线提供了常见的波数,或向管道系统内传播的总体模态。色散曲线还有助于洞察系统内部在不同的频率下的状况。我们看一看如何对色散曲线进行解析计算。
空心管道与刚性壁管道的模态
假设线性守恒系统在(z)方向均匀且无限延伸。其自由振动方程可写作:
(1)
其中 μ(z) 是质量密度,L(z) 是刚度算子,它取决于z,\; \frac{\partial}{\partial z},\; \frac{\partial^2}{\partial z^2},… 等参数。
方程的具体形式不固定。根据具体问题不同(比如梁、板或声腔),w一般可能与 1 、2 或 3 个空间变量构成函数关系。如果传播的是时谐波,那么 Eq. (1) 的解为 w(z,t) = Wei(ωt – kz),其中 W是波的振幅,ω 是角频率,k是波数。
把 Eq. (1)中的 w(z,t)替换掉,可获得色散/特征方程。其解是成对出现的波数,表示波在±z 方向的运动。波数可表征为:
- 传播(k) 的纯实数值)
- 衰减(纯虚数 k)
- 衰减振荡(k 的复值)
结构模态
下一步是分析计算结构的基本模态,例如纵向、剪切和弯曲波。本文的系统横截面始终不变,波沿 x正轴传播。为了计算纵向运动,我们使用了一个密度为ρ、杨氏模量为E的均匀弹性杆,其自由振动运动方程可基于 E\frac{\partial^2u}{\partial z^2}-\rho\frac{\partial^2u}{\partial t^2}=0 推出。利用与时谐波运动相同的原理,推导出色散关系为 k=\omega\sqrt\frac{\rho}{E},相位速度为 c_L=\frac{\omega}{k}=\sqrt\frac{E}{\rho},群速度为cg = cL。由于 cL 与 ω 和 k无关,因此所有谐波的运动速度相同。剪切波的色散关系的形式为k_s=\omega \sqrt\frac{\rho}{G} ,其中 G 是材料的剪切模量。
为了计算弯曲波,我们基于特定的假设前提而选择了 Euler-Bernoulli 和 Timoshenko 理论。Euler-Bernoulli 假设在弯曲过程中,梁的横截面始终为平面,且与中性轴垂直,同时忽略了转动惯量和剪切效应。这简化了许多方程项,最后得到一个易求解的四阶偏微分方程 EI \frac{\partial^4w}{\partial z^4}+\rho A \frac{\partial^2 w}{\partial t^2}=0。
上述假设唯一的问题是无法在高频下验证,因为高频波长与结构厚度基本相同。色散关系由 k_b=\bigg(\frac{\rho A}{EI}\bigg)^{1/4}\sqrt\omega 给出,对应的相位速度为 c_b=\bigg(\frac{EI}{\rho A}\bigg)^{1/4}\sqrt\omega,群速度为 cgb = 2cb。相位速度受频率影响,因此弯曲波具有色散性。由于频率分量更大,传播速度更快,因此波向外传播得更快。
Timoshenko 等理论引入了剪切效应,可以准确地描述高频特性。对于复杂的横截面,解析解是不可行的。
声学模式
圆柱管道内的声压场符合声波方程,它可以根据下列方程推导出:
其中n是周向模态阶数,Pn是振幅系数,Jn(krr) 是第一类贝塞尔函数,kz 是面外波数,θ 是圆周角。
径向波数 kr 取决于刚性壁的边界条件;即 Jn‘(krr)r=a = 0,其中 Jn‘(krr) 是关于 r 的贝塞尔函数的导数。对于给定的n,解/模式拥有多个值。相应地,面外波数通过关系式kz2 + kr2 = k2进行计算。
使用 COMSOL Multiphysics® 中的模态分析求解器
本文中的充液管道具有线弹性和均匀性。我们对流体进行纯声学分析,这说明它是可压缩、非粘性的正压流体。管道的每个模式均进行单独计算。示例数值模型的管道材料被设为钢,流体设为空气。材料属性如下:
| 材料属性 |
|---|
| E = 2e11 N/m2 |
| ρs = 7800 kg/m3 |
| ν = 0.3 |
| ρf = 1.25 kg/m3 |
| 空气中的声速, c = 343 m/s |
| ro = 0.05 m |
| t = 0.0025 m |
我们使用固体力学 接口和压力声学,频域 接口对模型进行了求解。此外,使用了模态分析研究类型,对每个频率对应的模态或面外波数进行了计算。模态分析假设模态为空间谐波;即 u(x,y,z) = u(x,y)eikzz。对于大多数面外波数 kz,我们可以在给定频率下对自动振动方程进行求解kz。
一些离散值——特征值——与传播或衰减模式的波数相互对应。模态分析研究步骤所触发的求解器能够确定这些波数及其振型。参数化频率扫描计算了不同频率下的波数。
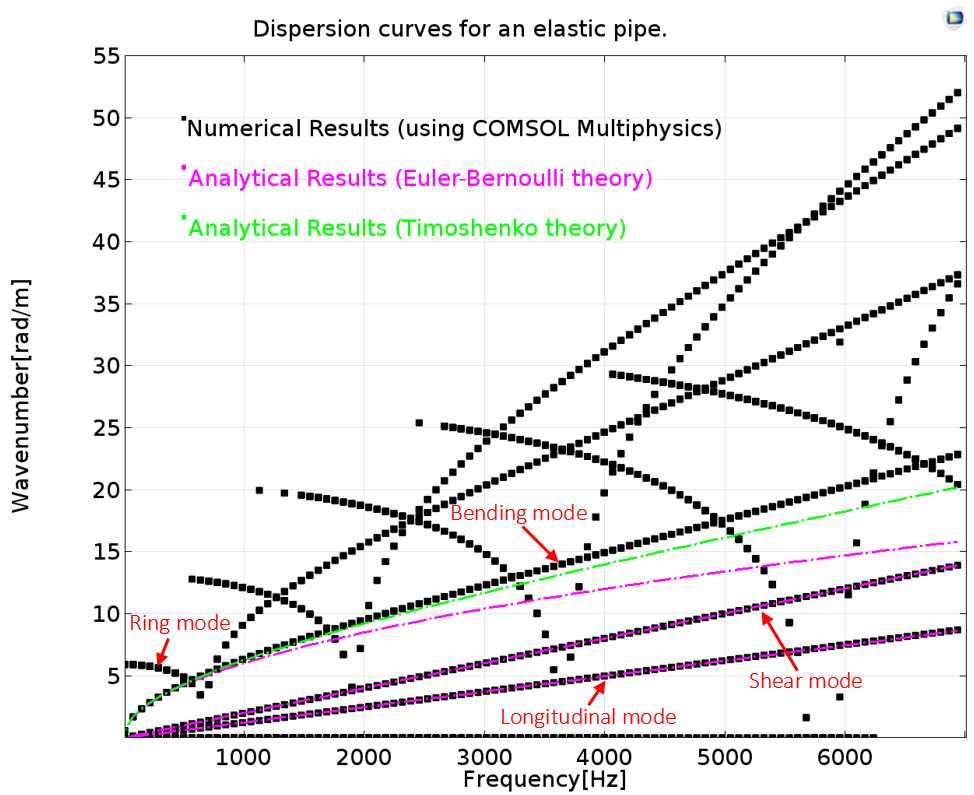
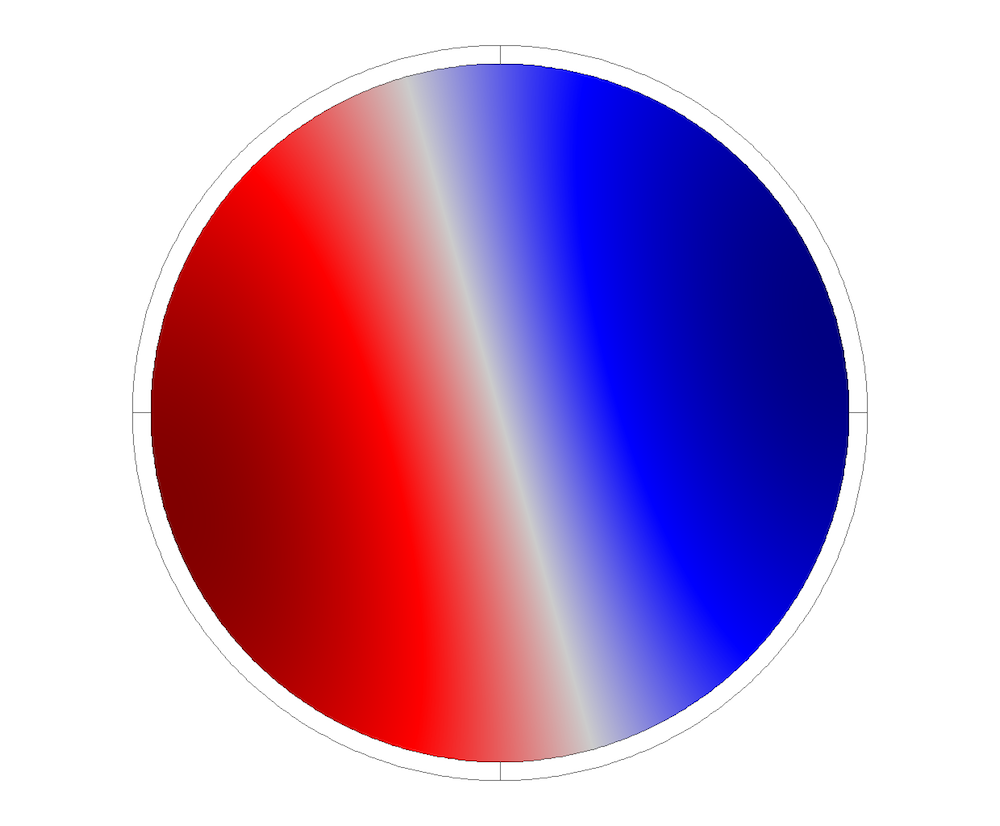
我们绘制了波数的实值,因为它对应于波的传播模态。横截面形状也是根据总位移而绘制的。我们采用了线条来读取色散曲线(见下图)。通过比较弯曲模态、剪切模态和纵向模态的解析解,我们更易对三者进行区分。可以观察到,约 6000Hz 处突然出现了一个模态,并由此处开始传播。有时模态特性可能在高频处发生变化(弯曲模态转变为剪切、纵向或扩张模态)。这种特性可以通过色散曲线轻易捕获。
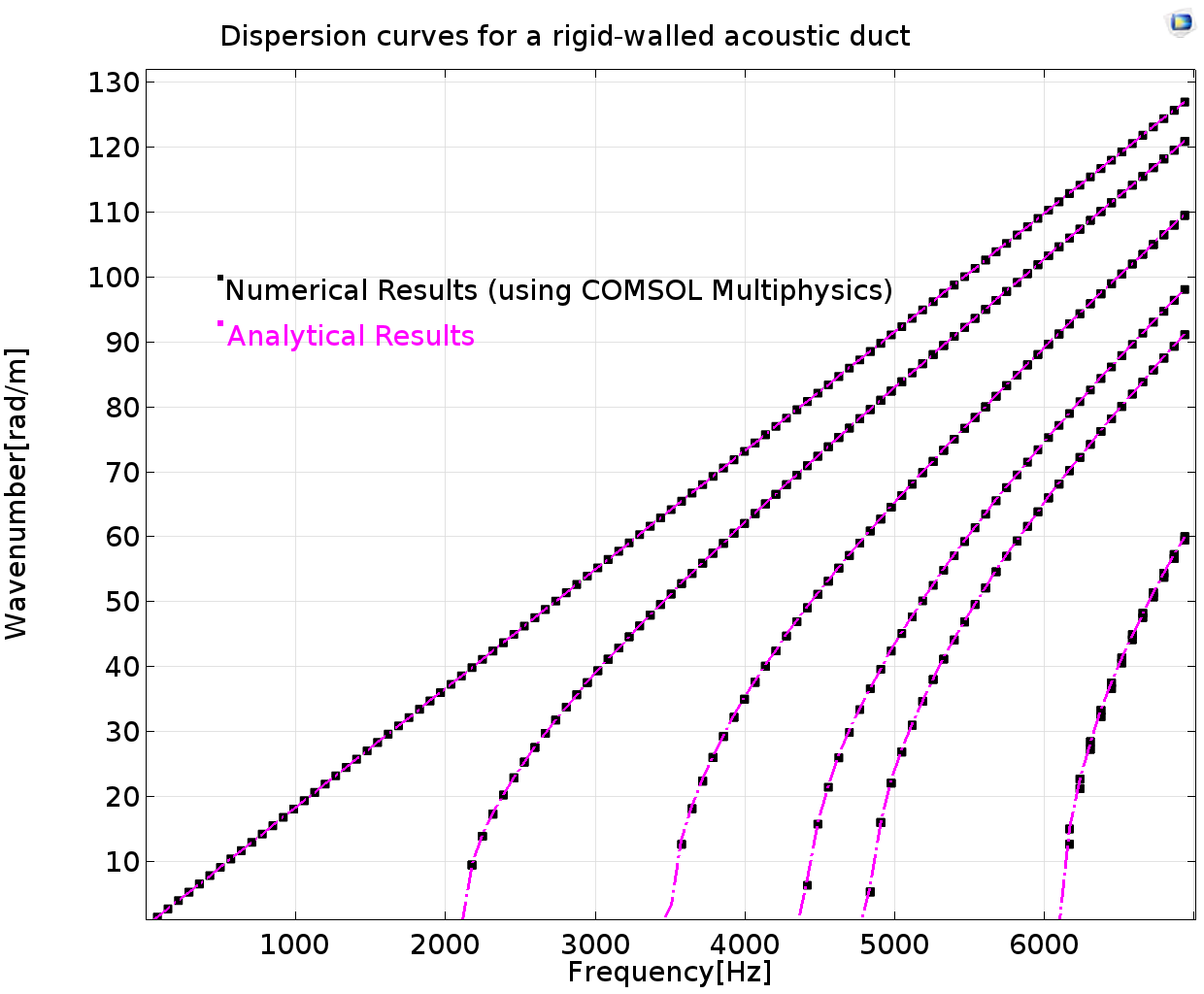
空心圆柱管道(左)和刚性壁声管(右)的色散曲线。
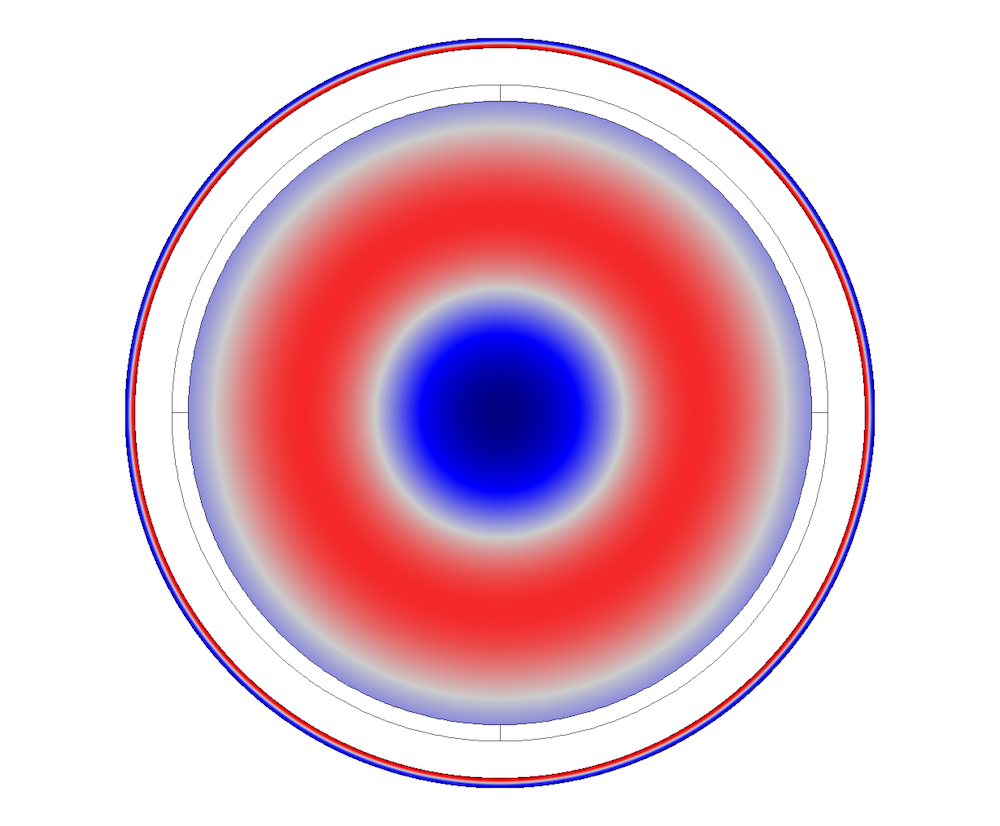
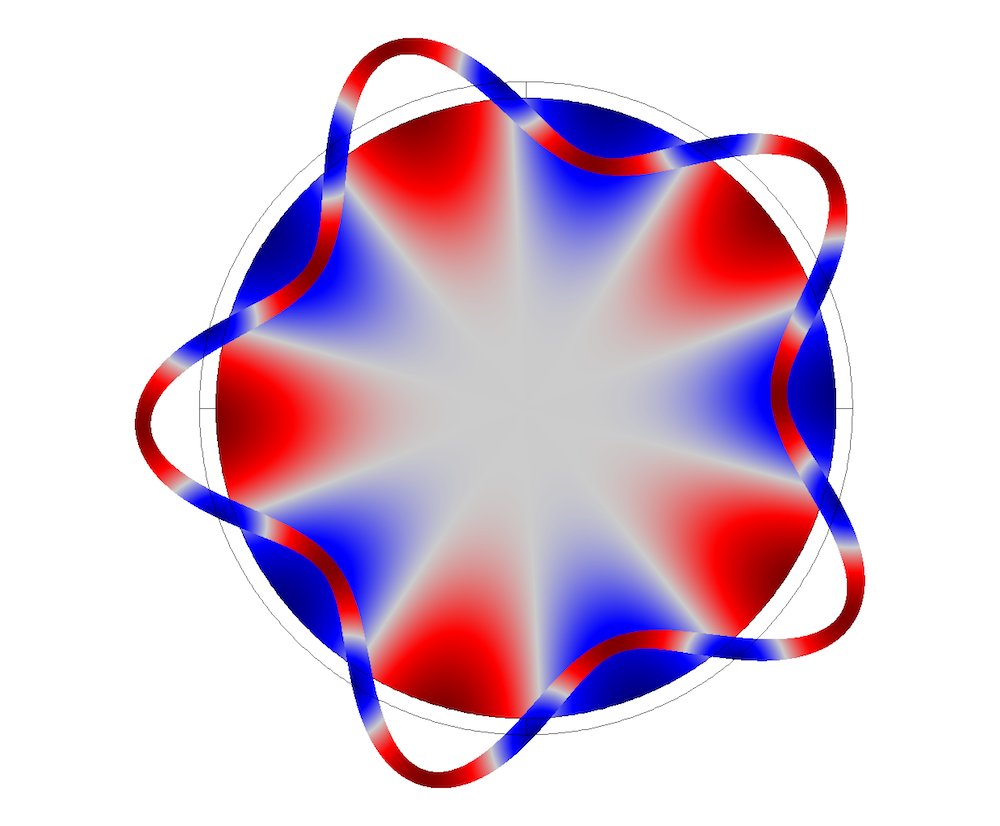
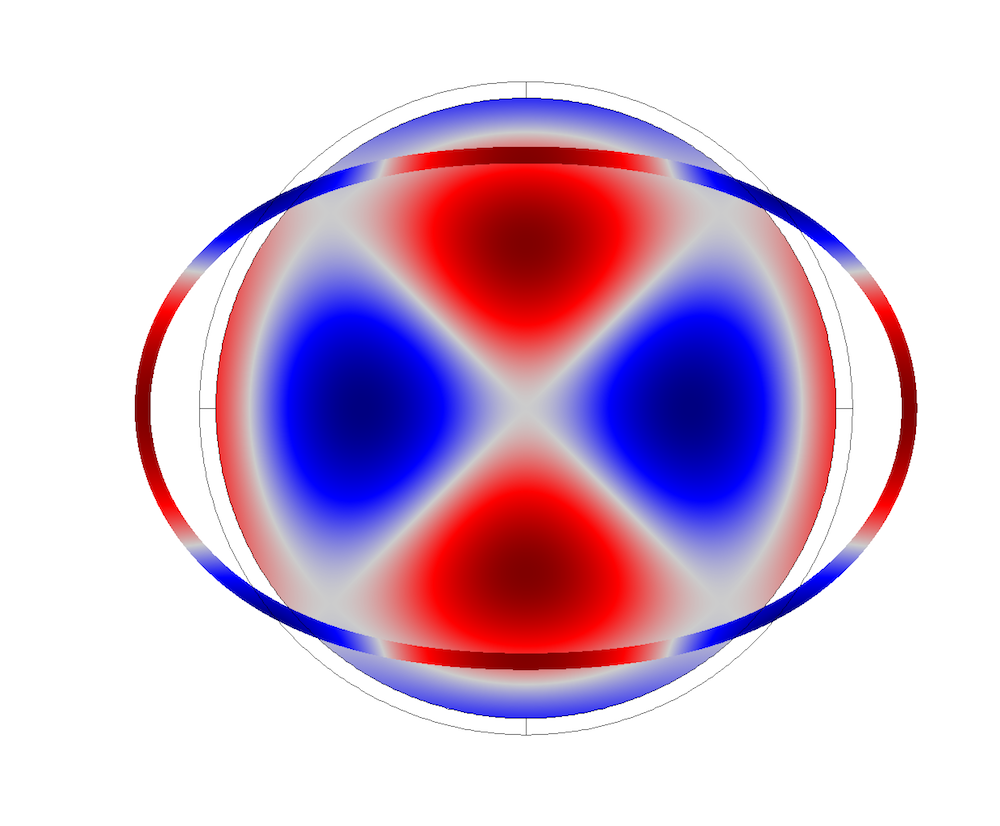
管道横截面振型。
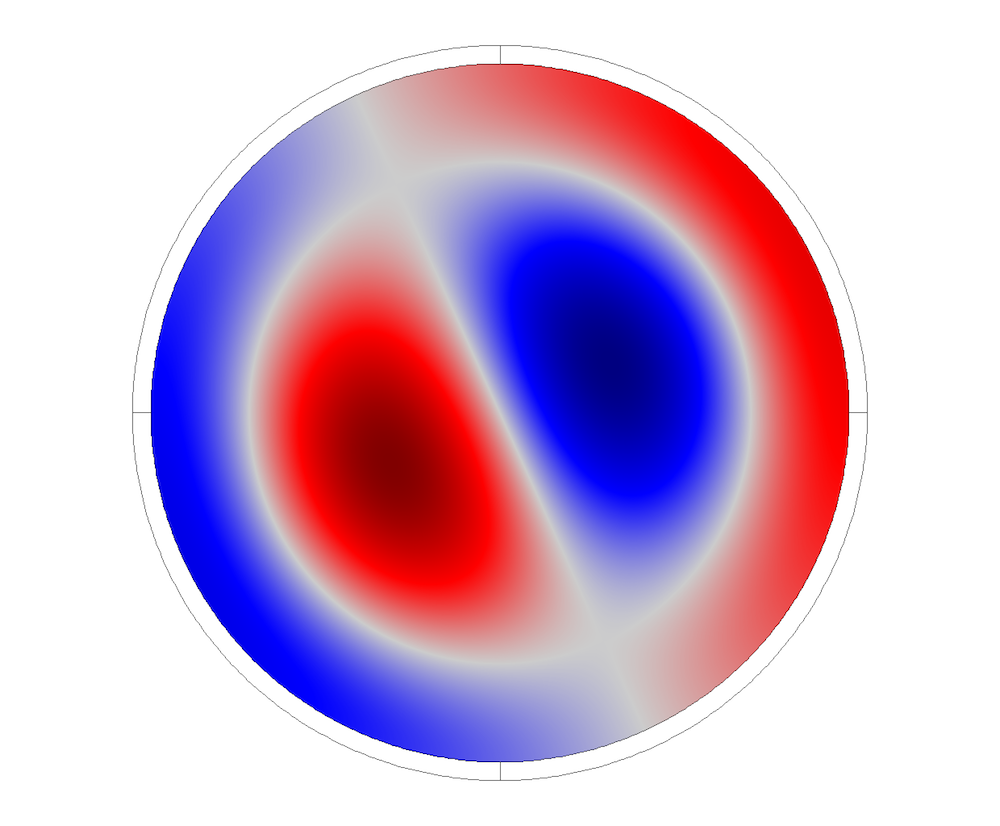
圆柱刚性壁管的色散曲线可使用相同的类比进行分析。前 6 个声学模式(上方右图)分别在大约 2000、3500、4300、4800 和 6100 Hz 处开始出现。我们对比了这些模态的解析解,并绘制了圆柱管的横截面形状,绘图还展示了管道横截面上的压力分布。
不同模态对应的压力分布。
我们将通过 COMSOL Multiphysics® 软件计算的波数与空心管道和刚性壁圆柱管的解析波数分别进行了对比。结果非常吻合,但是弯曲模态却存在明显的差别。原因是解析理论基于假设,不适用于高频。数值结果的可靠性主要体现在对研究域进行了恰当的离散化。
需要注意的是,每个波长必须使用足够多的单元(约 6 至 8 个二阶单元)才能精确地捕获波长。数值方法的另一个优点是,对于难以解析的复杂横截面(比如多层管道或形状复杂的横截面),它能“手到擒来”。在上方左侧绘图中,除了常规的模态(弯曲、径向、剪切),许多其他模态都可以在数值解中观察到。该数值随频率范围的增大而增加。“多余”的模态(比如环状模态)也具有物理意义,而且它们很难通过解析解来获得。系统的总体动态响是所有模态的叠加结果。
在更高的频率范围之内,系统的行为变得更加复杂。模态互相叠加,每个模态的特征都难以理解。这时,我们又将色散曲线搬来“救急”。
计算充液管道的波模态
下面,我们将计算充液管道耦合系统的波数。利用先前所述的方法,内部流体为空气和水的管道都可以使用 COMSOL Multiphysics 的模态分析求解器,对波模态进行计算。
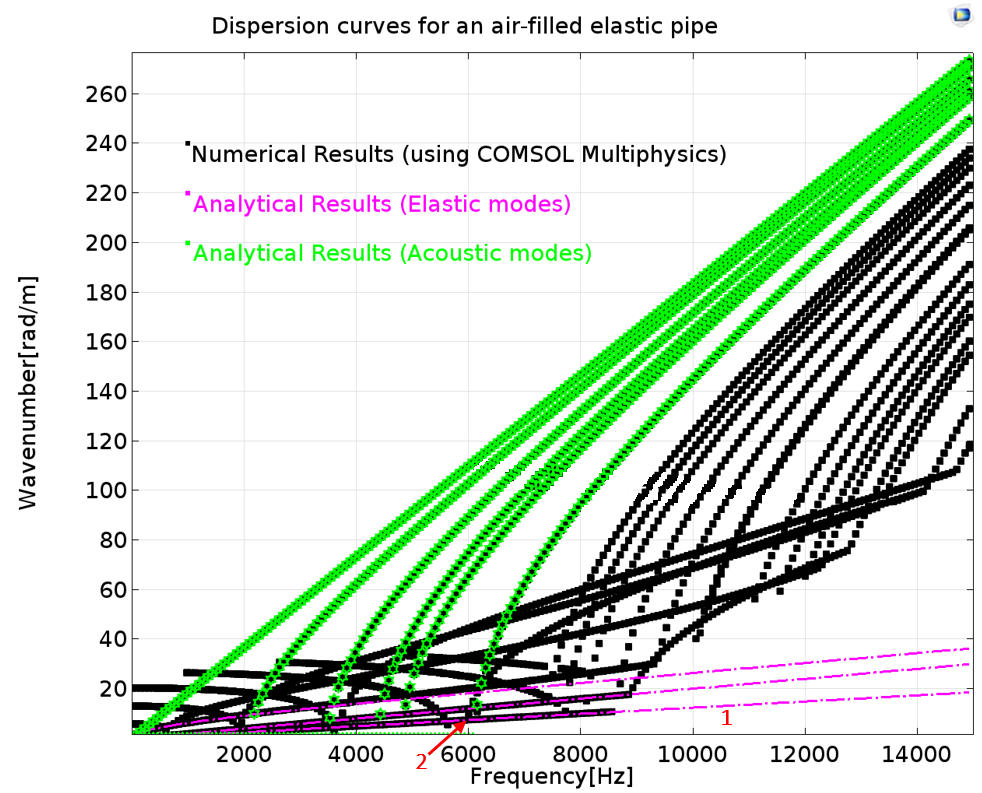
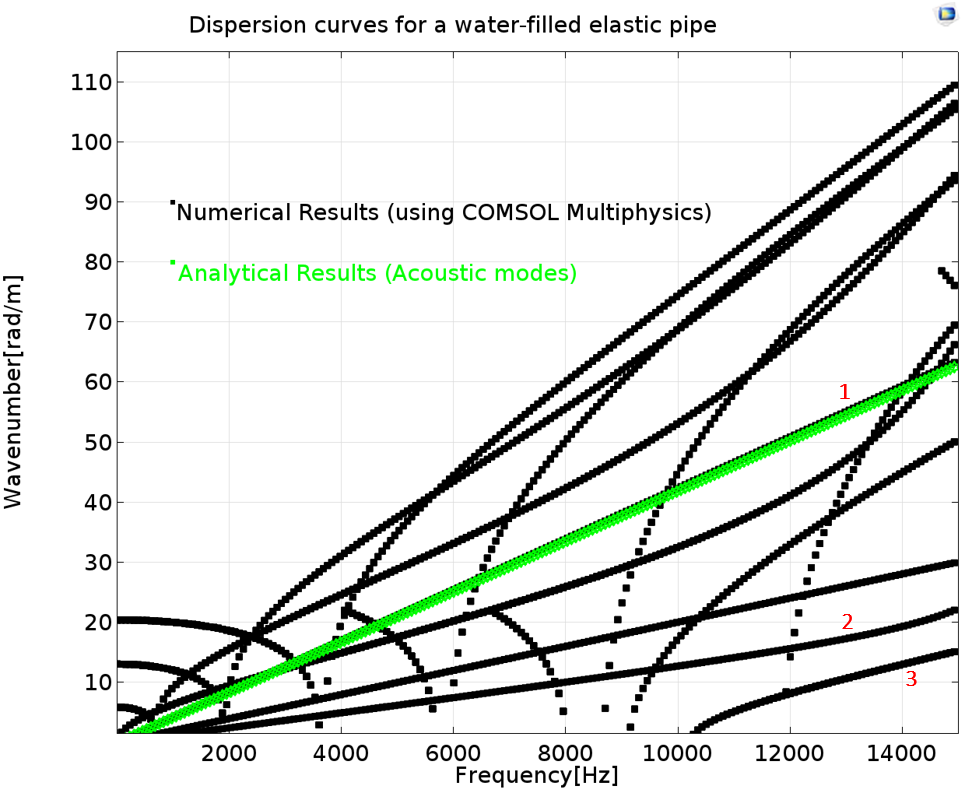
充满空气(左图)和充满水(右图)的钢管的色散曲线。
图片对比了充满空气的钢管的计算结果与未耦合的声学和弹性模式。流体很轻,对耦合系统的振动基本没有影响。
管道在低频下呈环状振动,此时可观察到环状模态。不过,由于泊松效应,弹性和声学部分存在弱耦合。随着频率的增加,弹性和声学部分的运动变为强耦合,突出表现为径向振动迅速加快。举例来说,分支 1 对应纵向模态,分支 2 对应耦合模态。尽管空气与钢之间的耦合很弱,但频率为 6000 Hz 时,扩张模式转变为声学模式。
下图显示了耦合系统的横截面振型。它相当于管道内的位移和流体域内的压力场。
充水管道绘图显示了强耦合行为。分支 1 显示了刚壁圆柱管道中的声波(纯声学模式)。考虑到分支 2,管道在低频下表现为真空状态。在高频下,流体和管道运动变为强耦合,且模式转换为第二声学模式。分支 3 初始时(刚出现时)为 10000 赫兹。该模式似乎与扩张结构模式趋向一致;在高频时,它再次转换为刚壁声学模式。我们可以通过类似方式来分析其他分支。
内部流体为空气的耦合弹性声波振型。
此外,利用色散曲线,我们还可以对系统进行高频动力学分析。对于有限长的系统,我们可以使用传播常数或波数高效地计算强制响应。
如果你希望减少系统的噪音辐射,可以考虑几种简单的技巧,比如使用由软橡胶制成的多层/夹层管道,并套上两层刚性外壳,或者设计一个复杂的横截面(可以是椭圆形)。借助色散曲线,我们很容易对这些复杂的结构进行测试。
不过,分析必须符合下列条件:
- 线弹性系统,或者在横截面方向而非长度方向上具有各向异性
- 恒定不变的横截面,适用于极长(无限长)波导
- 充分的有限元离散化,同时单元尺寸不宜太小,避免产生任何病态问题
结语
在本篇博客中,我们讨论了如何计算无限长多物理场系统的色散曲线,以及如何进一步分析系统的结构力学和压力声学。该分析利用了 COMSOL 的模态分析求解器。在后续博客中,我们将展示如何基于模态计算有限长导波管的强制响应。
参考文献
- F. Fahy and P. Gardonio, Sound and Structural Vibration: Radiation, Transmission and Response, Elsevier Academic Press, 2007.
-
C.R. Fuller and F.J. Fahy, “Characteristics of wave propagation and energy distributions in cylindrical elastic shells filled with fluid,” Journal of Sound and Vibration, vol. 81, no. 501518, 1982.
- A. Bhuddi, M.L. Gobert, and J.M. Mencik, “On the acoustic radiation of axisymmetric fluid-filled pipes using the Wave Finite Element (WFE) method,” Journal of Computational Acoustics, vol. 23, no. 3, 2015.









评论 (2)
HB Liao
2018-08-19期待:展示如何基于模态计算有限长导波管的强制响应。
Ajit Bhuddi
2018-08-20To compute the forced response on a finite length waveguide, one can decompose the displacements in to the summation of wave modes, i.e. [q;F]= SUM_(n=1 to n) A1 e^{-ik_n*x}+A2 e^{i*k_n*x} ……….Eq(1), where A1 and A2 are the amplitudes of incident and reflected waves, respectively. k_n is the wave number for different types of wave. Based on the boundary conditions, A1 and A2 can be computed and the complete response can be computed using Eq(1).