
分离式求解方法是 COMSOL Multiphysics® 软件的核心技术之一,它可以快速求解非线性多物理场(和单物理场)问题得到收敛解。你是否知道?我们还可以通过引入一个额外的全局方程来扩充这个求解方法,其中,全局方程能用于调整模型输入来实现所需的输出。今天,我们详细介绍如何使用这个方法。
加速求解器收敛速度
当遇到多物理场问题时,我们经常会通过求解非线性方程组的方法来处理。但这个方程组往往非常大,这意味着我们需要大量的时间和计算资源才能求解。
分离式求解器是一种加速求解器收敛的方法。该求解器通过使用一个完整的大型方程组或方程矩阵,并将其分解(或分离)为几个较小的矩阵的方法来处理。通常,这些矩阵中的每一个子矩阵都对应一个物理场。在求解过程中,软件将以分离步骤的方式来求解这些子矩阵之一。当逐步求解完所有的子矩阵后,求解器将检查收敛性,并根据需要进行迭代,直到实现收敛为止。
这种方法可以处理各种各样的问题,对于具有较高计算要求的三维模型尤为有效,并且在这些情况下,几乎始终是默认的方法。
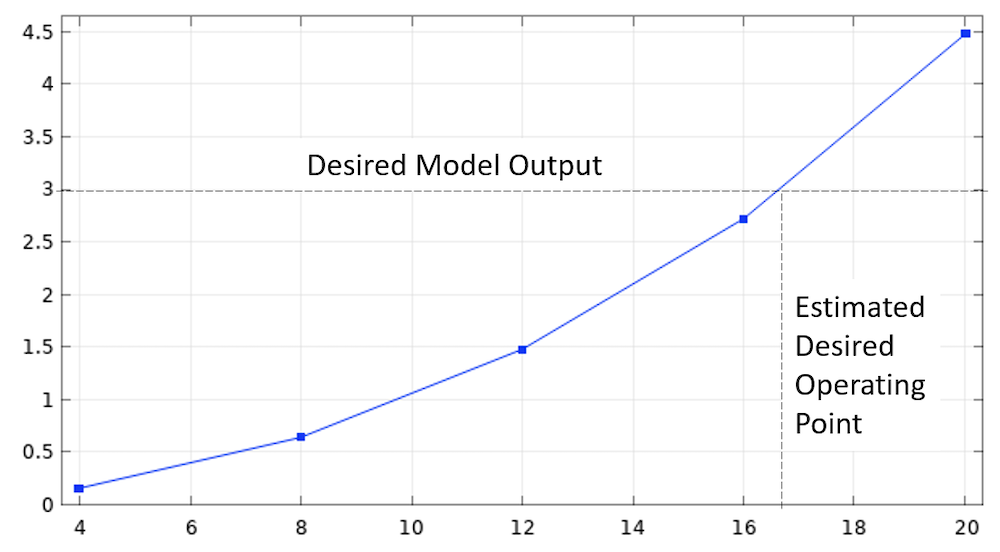
图1 输入值范围内的扫描可用于预测模型响应并估算所需的工作点。
通常,在求解模型时,存在这样一种情况,即我们不想改变几何图形,但又确实想根据我们设想的一个目标去更改某些其他模型输入。也就是说,我们希望模型产生一个特定的输出。
例如,我们可能想要获得所需的温度、热载荷、流速或任何其他派生值。从形式上来讲,这是一个优化问题,我们可以使用 COMSOL 软件的优化模块轻松解决。但是,对于只想改变单个模型输入的情况,使用优化模块可能会有些过头。我们在这里将介绍几种其他方法来调整输入以获得所需的输出。
获得这种模型输入的最简单方法是通过参数化扫描。也就是说,通过指定要更改的输入,提供要扫描的值范围,然后就能绘制输出与输入的结果图。从这个结果图中,我们可以直观看到并选择我们想要达到的目标点(图1)。
这是一种非常传统的方法,但是代价有些高。通常,响应曲线是非线性的,尽管通常它是单调的,我们常常需要在感兴趣的范围内求解两个以上的值,并且求解时间将随所求解值的数量而定。(请注意:这里我们可以使用“集群扫描”或“批处理扫描” 功能,但是这两个功能都需要大量的硬件资源,并且本文将假设我们有一些硬件条件的限制。)
使用全局方程的目标搜索方法
今天,让我们看看解决这个问题的另一种非常有效的方法:即将一个目标搜索方程引入分离式求解器中。我们可以使用以下方法非常简单地完成此操作:
- 使用全局常微分和微分代数方程 接口
- 仔细构建方程
- 对求解器设置做一些调整
下面,让我们来看一个典型的的示例。
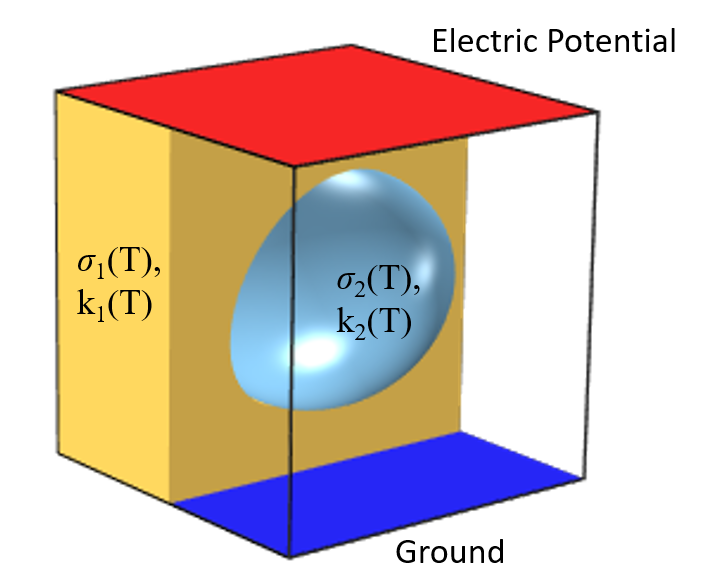
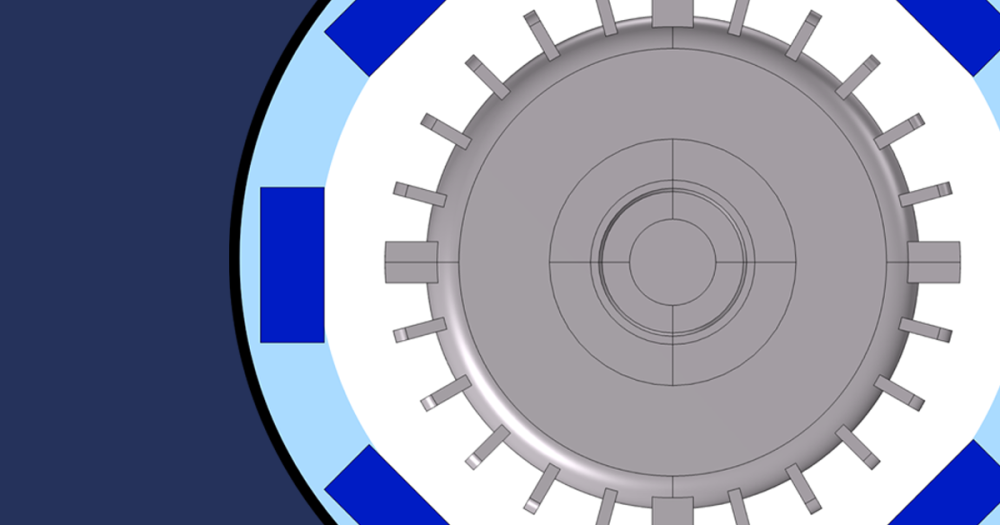
焦耳热问题示意图,其中两个电极之间包含材料。所有材料特性都是温度的函数。
以上图所示的焦耳热问题为例:施加了两个电极的一个介质中包含另一个具有不同电导率的介质,这种情况在组织消融模型中可能会出现,您可以查看这篇生物组织射频消融技术的仿真研究博客文章,了解相关案例应用。由于我们将在材料属性中考虑温度非线性,因此这种模型实际上可以产生一些非常复杂的结果,例如,在电热耦合分析中经常会陷入一些误区。
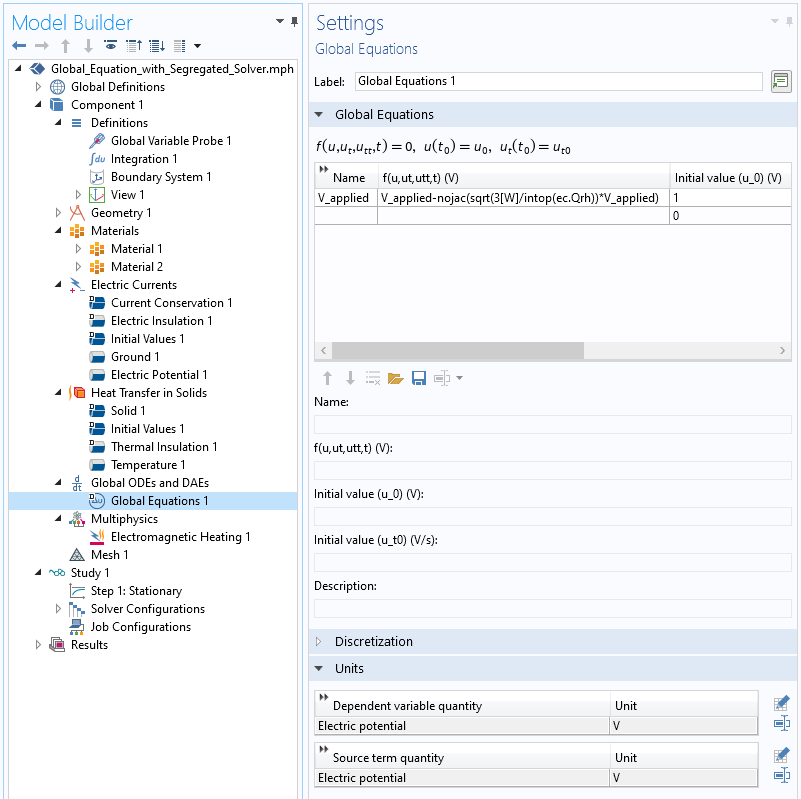
如何将额外的全局方程引入模型。
下面,我们来看具体的操作。假设我们想调整上述模型图中上部电极(红色区域)相对于另一个接地电极(蓝色区域)的电势,使包含在其中的介质电势为 3 瓦。施加在电极上的电势是变量 V_applied,我们将通过在模型中添加全局方程 来控制该变量,如上面的屏幕截图所示。我们输入的方程非常简单:
V_applied-nojac(sqrt(3 [W] / intop(ec.Qrh))* V_applied)
该方程将会在每次分离迭代中求解并更新 V_applied。所施加的电势根据使用积分算子计算出的损耗进行缩放。我们知道,至少在集总模型中,因为损耗与电势差的平方成正比,所以使用平方根。nojac() 算子中的所有内容都不会影响雅可比行列式,并且其中的项基于上一个分离步骤中的值,如果是第一步,则基于初始值。请注意,初始值 V_applied 必须为非零,并且适当的初始值将使得收敛更快。
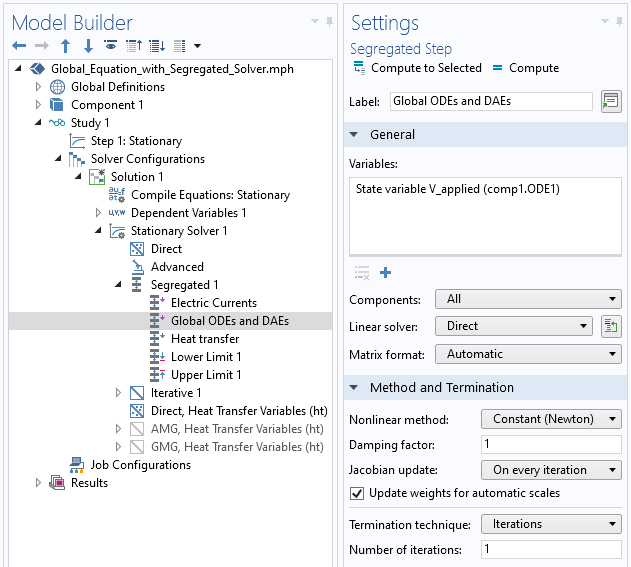
计算出电势之后用全局方程求解的分离式解器设置。
在分离式求解器设置中使用分离步骤计算电流之后,我们需要确保分离步骤已经求解,因为更新后的表达式是基于所计算的电损耗得出的。另外,我们还希望确保在计算电流之前或在求解全局方程之后计算温度场,因为当材料电导率与温度呈非线性时,这会影响损耗计算。
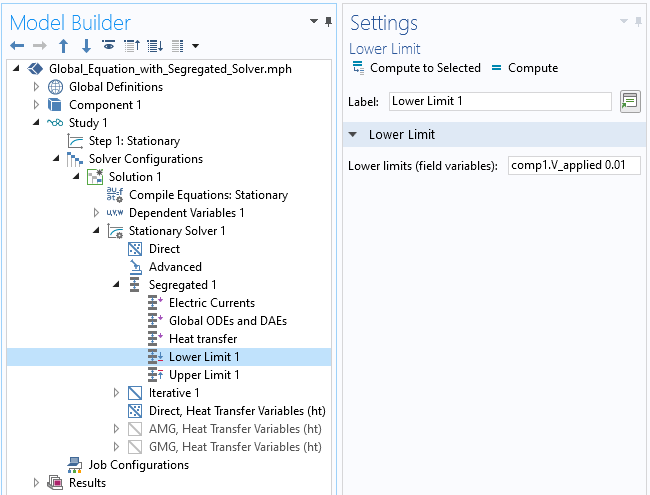
分离式求解器中的上限和下限特征。
分离式求解器还为要求解的变量提供上限和下限选项。也就是说,如果任何迭代将计算出大于或小于指定值 V_applied,则求解程序将仅使用极限值代替。就下限而言,这特别有用,因为我们永远不希望施加的电势变为零,因为初始值为零不可能进行进一步的更新。如果我们知道存在一些无法设置电势的值,则上限也很有帮助。
当我们使用分离方法求解此模型时,我们可能还希望监控 V_applied 以查看其在每次迭代中如何进行更新。我们可以通过实时监测仿真结果和下面屏幕截图中所示的设置来实现这个目的。分离式求解器还包括一个容差因子,该因子 乘以 稳态求解器 功能中定义的默认公差 0.001。使该数字小于默认值 1 将加强求解器的收敛标准。另外,还需注意,如果收敛非常慢,那么可以增加分离式求解器的迭代次数。
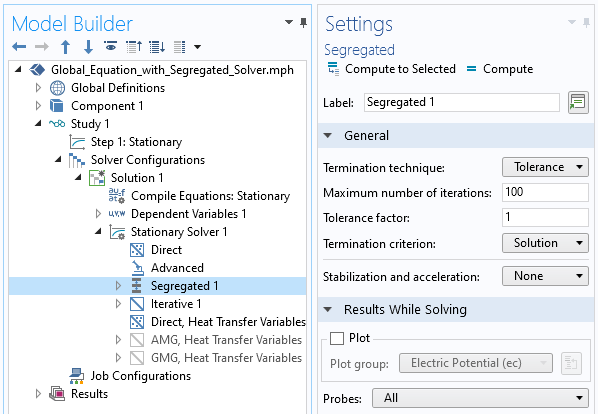
如何在每个分离迭代中绘制探针以及设置容差因子。
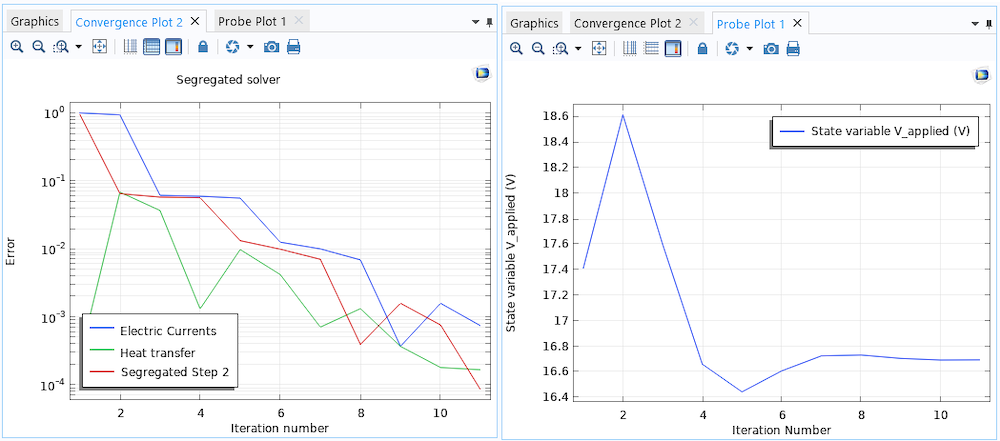
对于我们这里讨论的问题,收敛非常快。分离式求解器的收敛图和探针图如下所示。当然,我们永远不能保证非线性问题的收敛性(您可以查看 COMSOL 知识库中的这篇介绍:提高非线性稳态模型的收敛性),并且额外引进全局方程的更新通常会减慢收敛性。但是在很多情况下,我们可以放心地使用此技术,尤其是选择了一个合理的初始值时。应该注意的是,根据物理场和我们需要控制的值,可能需要不同形式的更新方程。在这种情况下,我们使用比例的平方根,但我们也可以在迭代之间使用线性或指数缩放。我们还可以将这种方法视为比例控制器或定点迭代方案。
这种方法的最大优点是,我们仅使用了一个解,即使用计算效率高的分离方法,即可达到设计点。与不使用全局方程相比,这个解可能需要进行更多的迭代,但是快速获得所需解的优势几乎总是超过成本。另外,如果我们想在时域求解,那么可以在不修改的情况下使用此方法,只要可以在每个时间步上满足全局方程即可。
当然,在某些情况下,这种方法可能会失败。这时,我们可以采用另一种方法,即完全耦合的方法而不是分离的方法,这个方法我们将在下一篇博客文章里介绍,敬请关注!
动手尝试
我们可通过以下按钮使用与该示例有关的模型文件:




评论 (0)