介绍几种计算辐射传热的方法

模拟辐射传热时，需要考虑辐射是如何从一个表面发射并被其他表面吸收的，以及表面与表面之间交换了多少辐射热。在辐射传热仿真系列博客的前两篇文章中，我们已经讨论了发射、反射和透射仿真，今天我们将通过介绍角系数的概念，以及计算表面与表面之间辐射传热的各种方法，来学习辐射传热仿真的基础知识。

这篇博客是辐射传热仿真系列博客的第3部分。点击此处，阅读第 1 部分和第 2 部分内容。

快速了解角系数

考虑两个薄且扁平的物体，如下图所示。假设红外辐射 (IR) 光可以在这些物体表面周围的空间内自由传播。这在真空中是成立的，并且在空气以及许多其他室温气体下也是合理的。假设无衰减传播可能不合理的情况包括：

• 吸收红外光的气体，例如水蒸气
• 高温气体
• 包含细小分散颗粒的气体
• 发生化学反应的气体

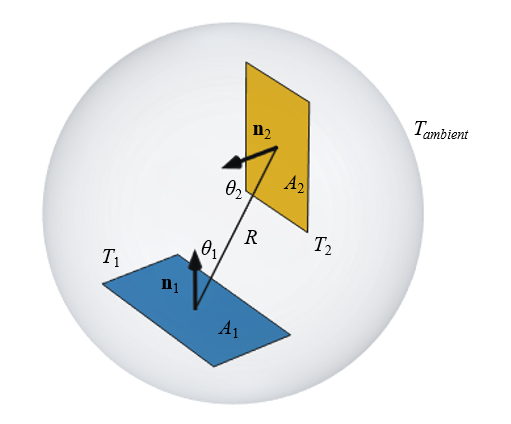
在不同温度下，两个等温物体之间会发生辐射传热。这两个物体可以被认为放置在一个封闭的环境内，热量传递的多少取决于物体的尺寸和方向，并且只会发生在彼此相对的表面之间。

假设这两个物体处于不同的恒定温度下。除了这两个物体之外，我们关注的模型中没有其他任何内容，但仍需要定义所有未模拟的周围空间。我们需要定义一个恒定的温度，称为环境温度或背景温度。虽然我们不会明确地模拟这个环境空间，但为了方便器件，通常假设一个温度恒定的封闭表面。

考虑第一个物体及其发出的所有辐射能，其中一部分辐射热通量流向环境，另一部分流向第二个物体。现在我们引入 角系数 的概念，它是从表面 1 (A_1) 发射到表面 2 (A_2)的辐射分量，记作 F_{12}。假设辐射度均匀且没有中间阻挡面，那么表面 1 与表面 2 的角系数为：

当系统中有两个以上的表面时，表面之间可能存在直接辐射传热的情况，因此我们将角系数写为 F_{i j}，其中 i,j 是模型中所有 N 个相互作用的表面的指数。在任意两个表面之间，互易关系：A_i F_{i j}= A_j F_{ji} 成立。

注意，如果一个表面是凹的，那么 F_{i i}>0。此外，辐射到环境的热通量是通过环境角系数：F_{i \rightarrow amb}= \left( 1 – \sum_{j=1}^N F_{ij}\right) 定义的。对于封闭的空腔，环境角系数为零。

计算辐射传热的三种方法

有三种方法可以计算辐射传热：

1. 直接面积积分法
2. 半立方体法
3. 射线发射法

1. 直接面积积分法

直接面积积分方法的原理是对所有相对的表面对进行双重积分，只要表面之间没有障碍物或阴影，就可以使用它。这种方法已被证明是准确的，其准确度仅由辐射积分阶次控制。

这种方法始终满足互易关系，但如果离散化太低并且网格非常粗，那么对于封闭空腔，环境角系数可能不为零。如果单元很多，直接面积积分会使计算量增大。此外，由于不考虑阴影，它主要用于模拟小型凹腔，因此在实践中很少使用。

2.半立方体法

如下图所示，我们可以从概念上来理解半立方体方法。考虑一个表面单元，围绕该单元绘制五个边界，并将它们均一像素化。然后，将环绕该单元面投影到这些像素化边界上，并计算与每个面相关联的像素数，确定来自环绕面的辐射热通量以及辐照到该单元的热通量有多少，并对每个表面重复此操作。

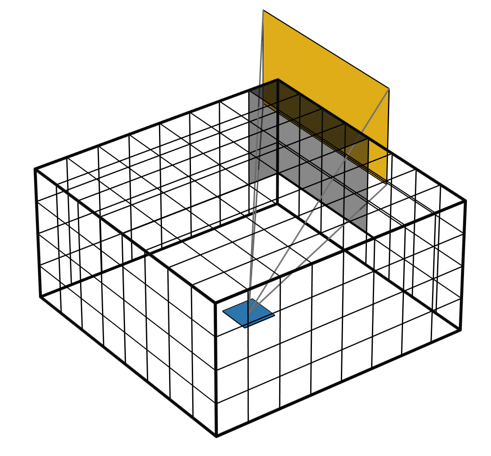
半立方体方法通过将环绕单元的面投影到一组像素化边界上来计算辐照度。

环绕面的阴影可以通过 z-buffering 高效地求解，因此计算成本很低。这种方法的单一设置，即 辐射分辨率 控制着像素数。互易关系的精度会随着辐射分辨率的提高而提高，封闭空腔环境的角系数将始终为零。

3. 射线发射法

射线发射方法适用于存在角度相关的发射率、镜面反射率或半透明的表面。射线发射法，顾名思义，就是在空间中发出射线。但需要注意的是，这是一种 反向 射线追踪方法。从每个单元的评估点出发，向外投射一组光线，用于确定该方向的辐照度。因此，可以将这些射线想象成与入射辐射方向相反。这些射线代表对环绕半球形空间内总辐照度的有限采样。

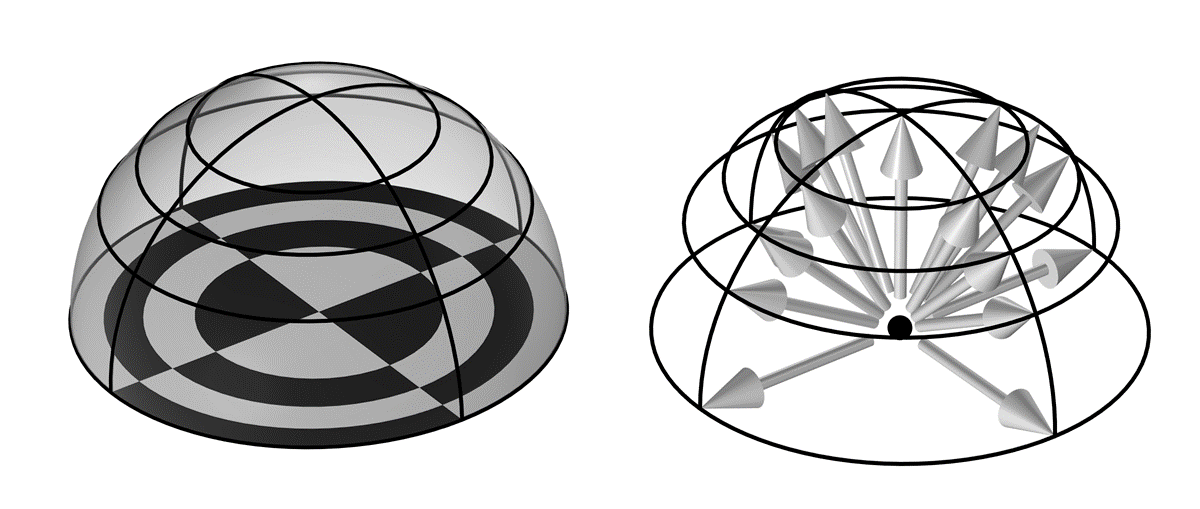
根据一个辐射分辨率为4 的三维半球体的离散化来说明射线发射方法。基础棋盘格（左）被细分为 16 个面积相等的图块。箭头指向每个图块在半球上的角落位置（右）。

射线发射法有 6 个可以更改的设置以及单元阶次。其中最重要的是要理解 辐射分辨率，它定义了光线在半球体（三维）或半圆（二维）上的初始分布，如上图所示，辐射分辨率为 n_{res}=4。

该方法首先将周围环境在三维中细分为 n_{res}
^2 个（或者在二维中细分为 n_{res}^2 个）图块，然后在每个图块的角绘制一条射线。这些图块具有相同的角系数，也就是说通过努塞尔数类比，每个图块在下平面上的投影面积是相等的。对于半圆（二维），如下图所示，将周围环境分为 n_{res} 个图块，每个图块在平面上的具有相同的投影面积。请注意这如何导致光线的角度分布不均匀，如下图所示。

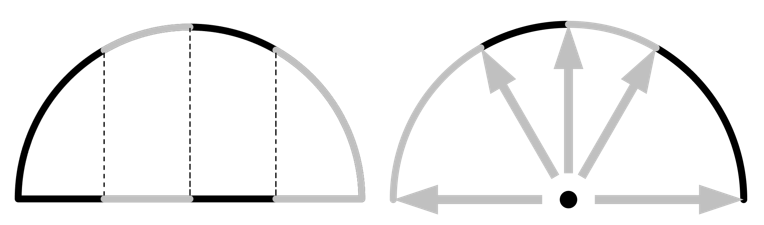
二维情况下的射线发射法。半圆（左）的每个扇区在下平面的线上的投影面积都相等。箭头指向每个图块的角（右）。

当光线向外投射时，本质上是查询来自该方向的热通量，然后将其与来自相邻光线的热通量进行比较。如果按照容差 设置所定义的，热通量存在差异，那么射线发射方法将在两条光线之间引入额外的光线，最多可达到最大自适应数 选项中指定的数量。当光线碰到镜面反射或透射表面时，还会从该表面发射出额外的光线，直到达到最大反射次数。将最大反射次数的默认值设为 1000 是合理的，除非是在镜面反射率大于 0.99 的空腔内进行多次反射。

仅当存在与角度相关的发射率表面时，角相关属性 设置才适用。与 插值函数 选项相比，默认的 全 分辨率设置不仅最准确，而且计算量最大，您可以在其中指定角度相关函数的采样精度。

首先，为确保结果的可靠性，我们需要研究辐射分辨率 和最大自适应数，因此了解这些设置之间的相互作用非常重要。让我们看一个二维示例，并考虑从中心单元发出的射线。应该注意的是，这只是一个可视化视图，计算射线本身是不可绘制的。假设存在一个单位发射率不变（相当于零反射率和温度恒定的半圆，这意味着每条射线探测到的辐射负载相同。在这种情况下，即使是最小的辐射分辨率也会得到正确的热通量。更高的分辨率（更多的光线）并不会获得更高的精度，也不会触发任何自适应。

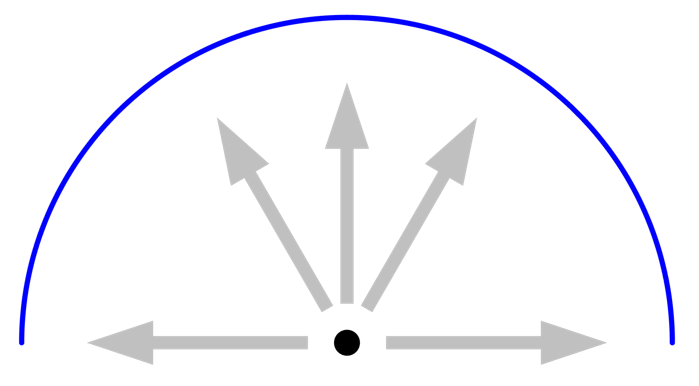
接下来，我们在刚好与其中一个射线方向重合的角度引入一个小物体，它也有单位发射率但温度不同。此时，这条射线与相邻射线将探测到不同的负载，并且角空间被细分，如下图所示。增加最大自适应次数将会提高精度，但不需要提高射线分辨率，因为其中一条初始射线已经探测到了小物体。射线的这种自适应性是基于从不同射线感应到的辐照度不同而进行的，因此，如果一个单一表面的辐射通量在空间变化，这种自适应性也会起作用。

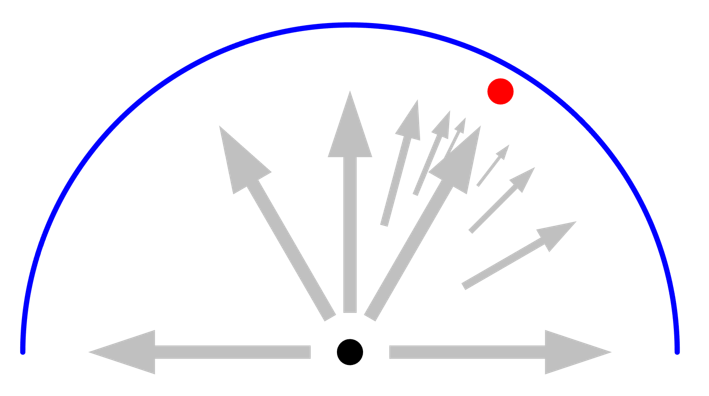
引入一个可被其中一条射线探测到的小物体，将导致相邻空间中的射线自适应。设置更高的自适应数将会提高精度。

最后，我们来看另一个与初始辐射分辨率方向不重合的另一个角度上的小物体。对于这种情况，最大自适应数是多少无关紧要。第二个小物体永远不会被任何初始光线“探测到”。要探测到第二个物体，必须提高辐射分辨率。

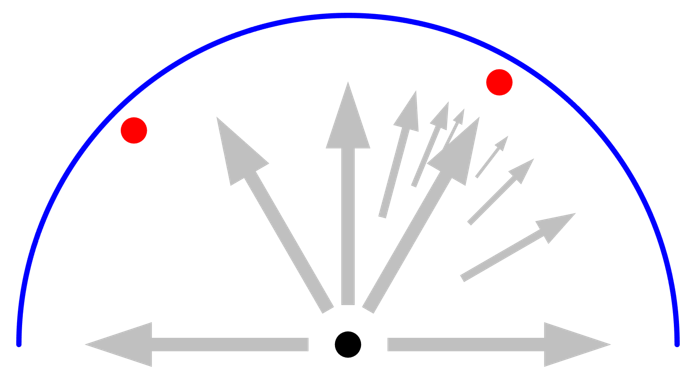
按照分辨率的定义，如果一个小物体没有被任何一个初始射线看到，附近的射线就不会进行任何自适应，它将被错过，这时就需要提高辐射分辨率。

使用辐射组

除了所有上述方法外，我们还可以使用 辐射组。通过选择只能相互看到的边界集可以降低计算成本，尤其是在一个包含多个不同空腔的模型中。但是，必须小心使用组功能，因为如果分组不正确，可能会产生错误的结果。

当一组不同的表面无法相互看见时，使用 组 功能是合理的。左图中不同的颜色表示合理的分组。右图显示的情况不太适合使用组功能 。

其他表面对表面设置

对于包含移动或变形物体的模型，有必要更新角系数，由角系数更新阈值 设置控制。虽然每次非线性迭代中的默认更新设置提供了最准确的结果，但计算成本可能较高。可以完全关闭角系数更新，这对于一个正在移动或变形的物体（它对角系数的影响可忽略不计）来说是可行的，也可以定义更新周期或通过用户自定义的表达式进行更新。

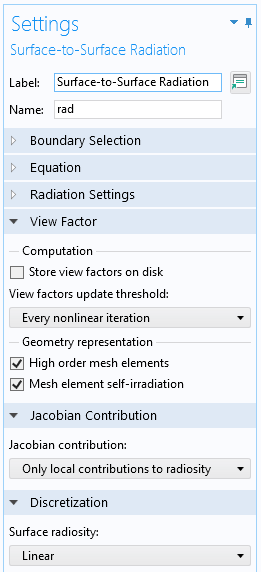
表面对表面辐射 接口的 角系数 设置。

角系数 设置还允许用户将计算出的角系数存储到磁盘。对于较大的模型，这可以节省时间，但会大大增加磁盘上模型文件的大小，尤其是使用 Hemicube 方法时。此设置只能在几何体不变的情况下使用。

如果几何形函数高于线性，就可以使用 几何表示 设置。如果增加离散化，这些选项将考虑单元的曲率。

最后，雅可比矩阵 默认设置为 仅对辐射的局部贡献。自 COMSOL Multiphysics^® 软件 6.0 版本开始，这个默认设置将降低内存使用率并加快求解速度。但是，如果模型是纯粹的辐射冷却，并且表面之间的温度变化很大时，它可能会求解失败。如果您观察到不收敛，请将这个设置更改为 包含总辐射的贡献。

计算和绘制角系数

我们在之前的博客中提到过，如果有几组表面，如何计算它们之间的角系数？有时，绘制从一个表面到模型中所有其他单元的角系数也很有帮助。这可以通过 element(order,expression) 算子对每个单元执行高斯积分的来实现。积分的阶次由第一个参数给出，为了计算角系数，我们使用表达式中的 radopu() and radopd() 算子。例如，绘制表达式：

element(1,comp1.rad.radopu(S1,0))/intS1(1)/dvol

将逐个单元地计算由积分算子 intS1() 定义的一组从表面到模型中其他所有表面的角系数。

变量 S1 应在辐照的表面集上被定义为 1，在所有被辐照的表面上被定义为 0。下图就是一个这样的示例。通过额外除以被辐照单元的大小，即变量 dvol，会得到一个对应于一组表面的辐照强度的图，如下图所示。

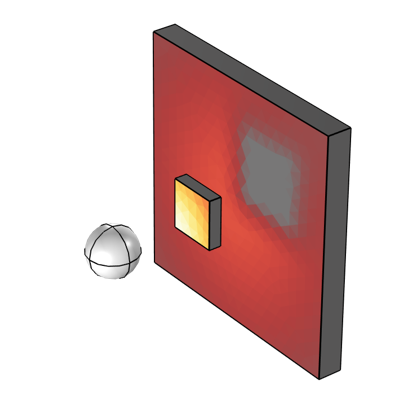
从一个球体到两个块状物体的辐照图，这两个块状物体有一部分相互遮挡。

结束语

在这篇博客中，我们研究了模拟无参与介质包围的表面对表面辐射传热的三个关键概念。首先，我们研究了由热表面发出热辐射的不同方式。接着，研究了入射到表面的辐射是如何被吸收、反射和传递的。最后，讨论了角系数，以及如何计算和更新它们。学习完这些，我们就可以非常自信地对热辐射问题进行模拟了！